POLIEDRI DIEDAR Unija dve poluravni sa zajedninom graninom

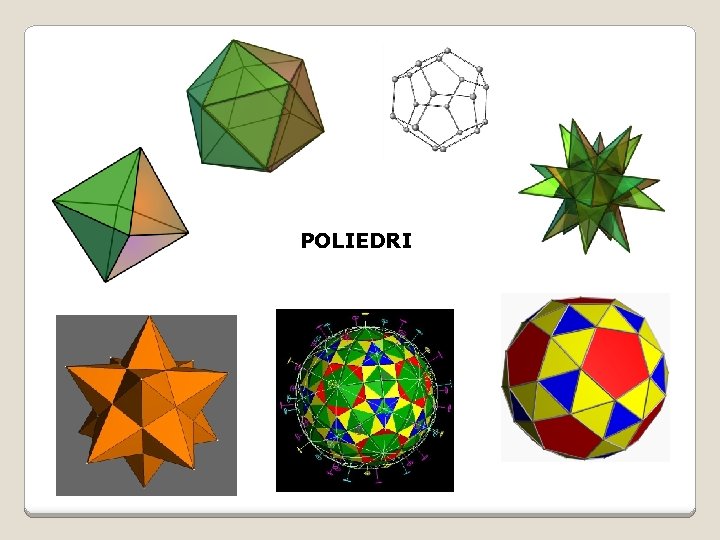
POLIEDRI

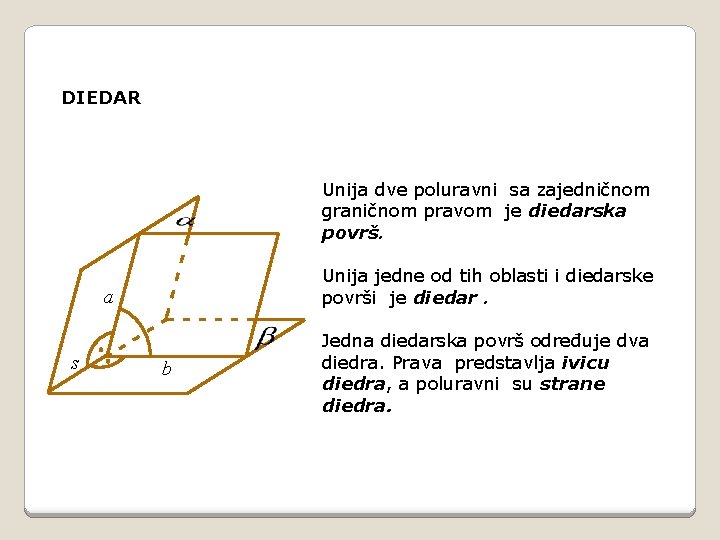
DIEDAR Unija dve poluravni sa zajedničnom graničnom pravom je diedarska površ. Unija jedne od tih oblasti i diedarske površi je diedar. a s b Jedna diedarska površ određuje dva diedra. Prava predstavlja ivicu diedra, a poluravni su strane diedra.

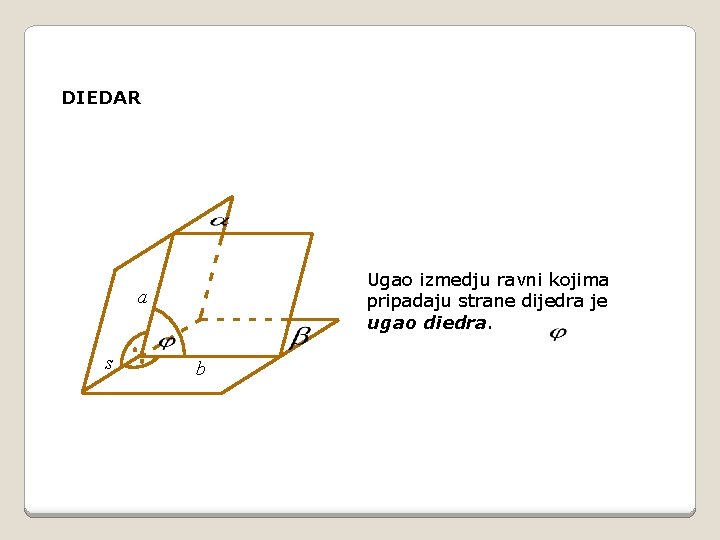
DIEDAR Ugao izmedju ravni kojima pripadaju strane dijedra je ugao diedra. a s b

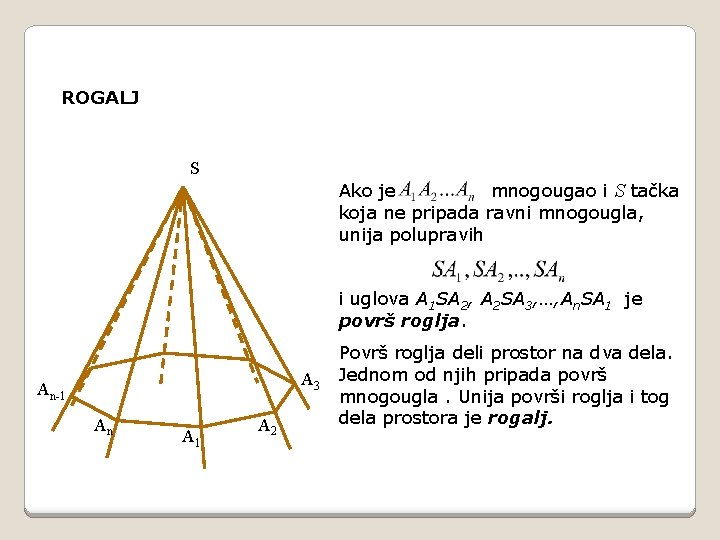
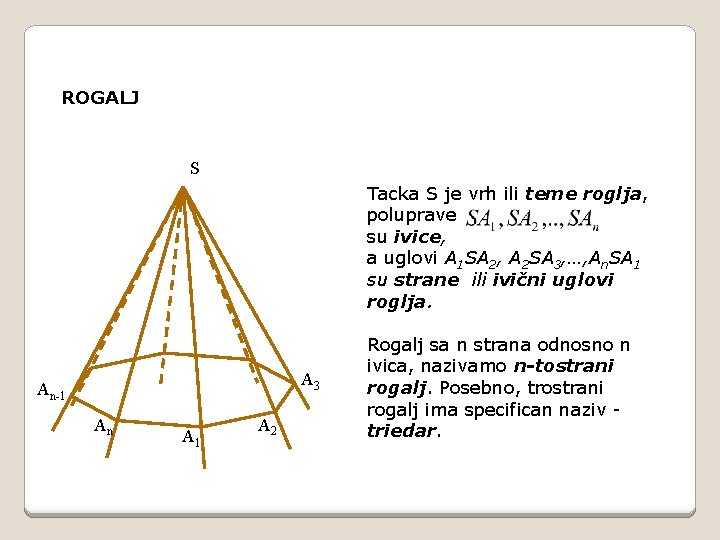
ROGALJ S Ako je mnogougao i S tačka koja ne pripada ravni mnogougla, unija polupravih i uglova A 1 SA 2, A 2 SA 3, …, An. SA 1 je površ roglja. A 3 An-1 An A 1 A 2 Površ roglja deli prostor na dva dela. Jednom od njih pripada površ mnogougla. Unija površi roglja i tog dela prostora je rogalj.

ROGALJ S Tacka S je vrh ili teme roglja, poluprave su ivice, a uglovi A 1 SA 2, A 2 SA 3, …, An. SA 1 su strane ili ivični uglovi roglja. A 3 An-1 An A 1 A 2 Rogalj sa n strana odnosno n ivica, nazivamo n-tostrani rogalj. Posebno, trostrani rogalj ima specifican naziv triedar.

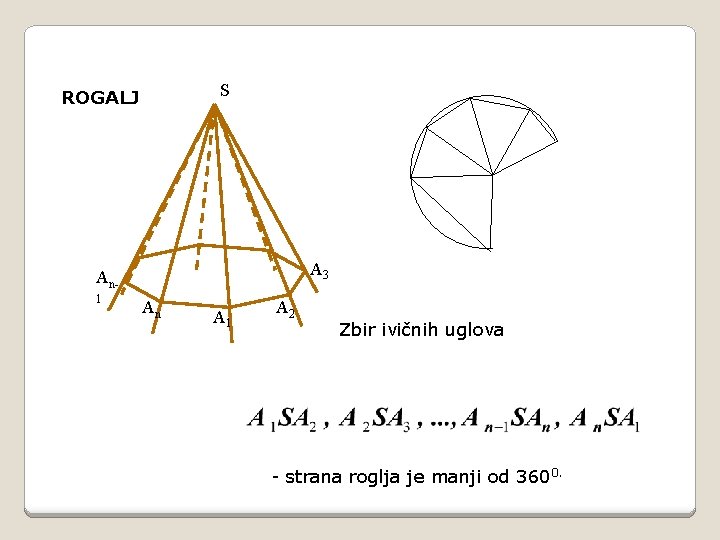
S ROGALJ A 3 An 1 An A 1 A 2 Zbir ivičnih uglova - strana roglja je manji od 3600.

POLIEDAR Skup površi mnogouglova takvih da je svaka stranica svakog mnogougla ujedno i stranica jos samo jednog mnogougla, obrazuju zatvorenu površ koja se naziva poliedarska površ. Deo geometrijskog prostora koji ograničava (zatvorena) poliedarska površ je unutrasnjost poliedarske površi. Unija poliedarske površi i njene unutrašnjosti je poliedar.

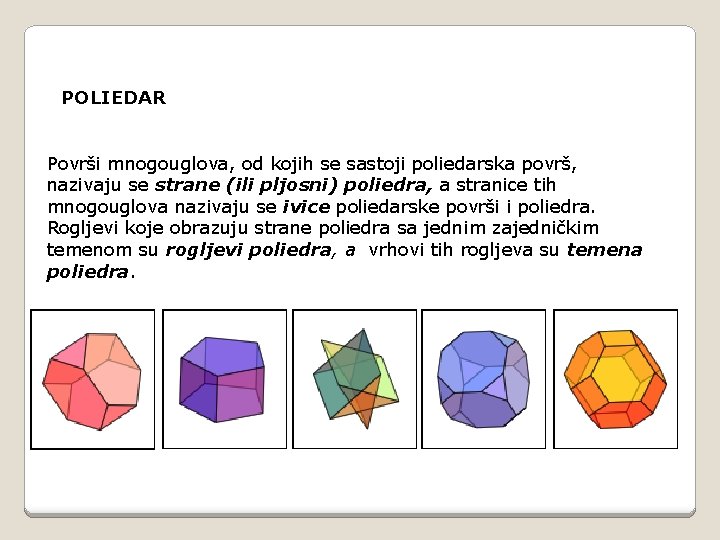
POLIEDAR Površi mnogouglova, od kojih se sastoji poliedarska površ, nazivaju se strane (ili pljosni) poliedra, a stranice tih mnogouglova nazivaju se ivice poliedarske površi i poliedra. Rogljevi koje obrazuju strane poliedra sa jednim zajedničkim temenom su rogljevi poliedra, a vrhovi tih rogljeva su temena poliedra.

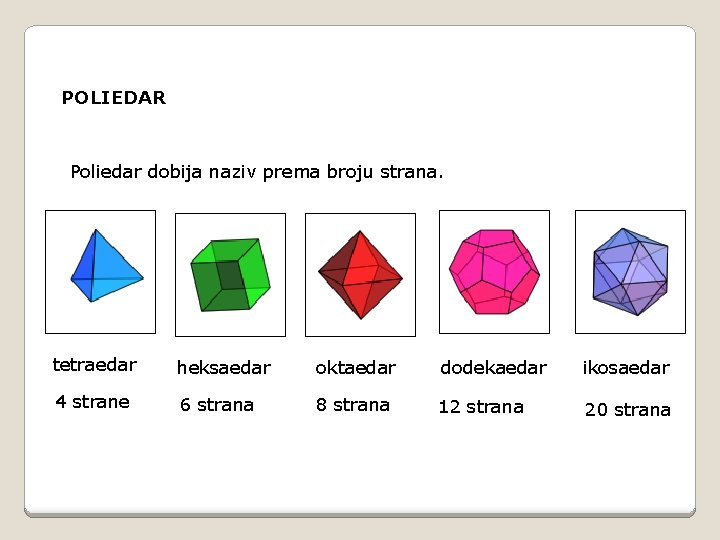
POLIEDAR Poliedar dobija naziv prema broju strana. tetraedar heksaedar oktaedar dodekaedar ikosaedar 4 strane 6 strana 8 strana 12 strana 20 strana

POLIEDAR Poliedri mogu biti konveksni i nekonveksni-konkavni. Poliedar je konveksan ukoliko svaka duž koja spaja njegove dve proizvoljne tačke pripada tom poliedru, u suprotnom slučaju poliedar je nekonveksan odnosno konkavan.

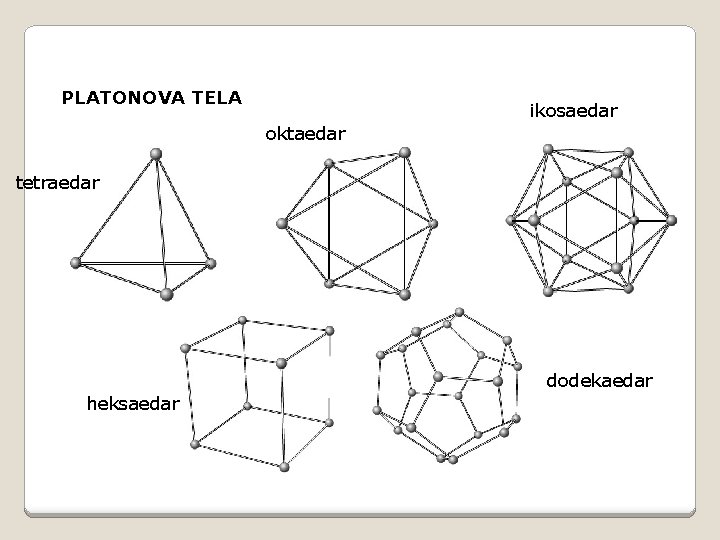
PLATONOVA TELA ikosaedar oktaedar tetraedar dodekaedar heksaedar

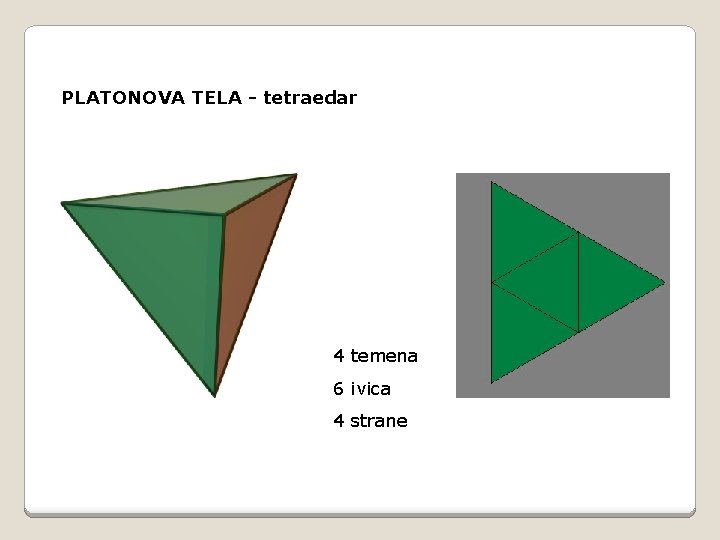
PLATONOVA TELA - tetraedar 4 temena 6 ivica 4 strane

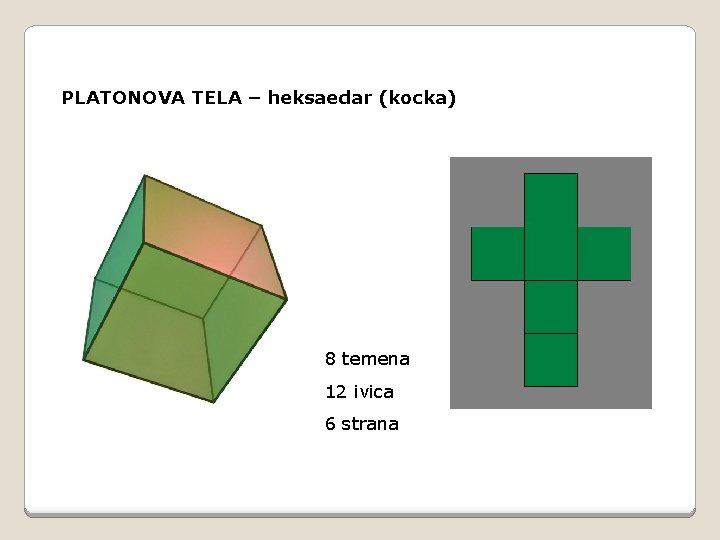
PLATONOVA TELA – heksaedar (kocka) 8 temena 12 ivica 6 strana

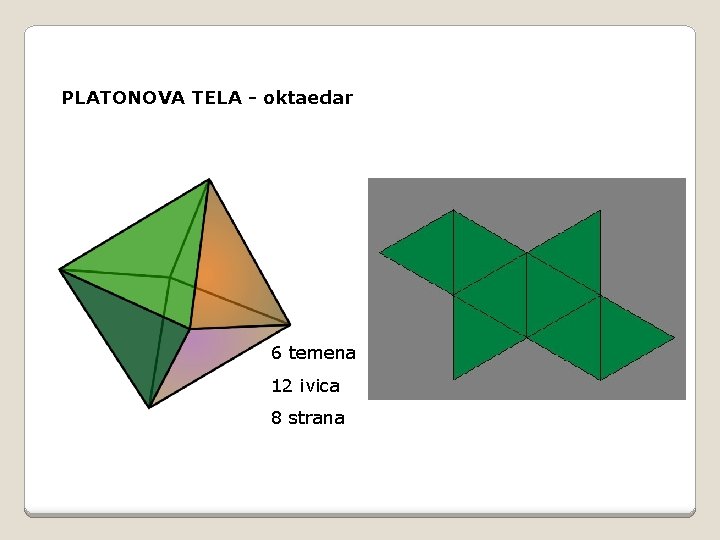
PLATONOVA TELA - oktaedar 6 temena 12 ivica 8 strana

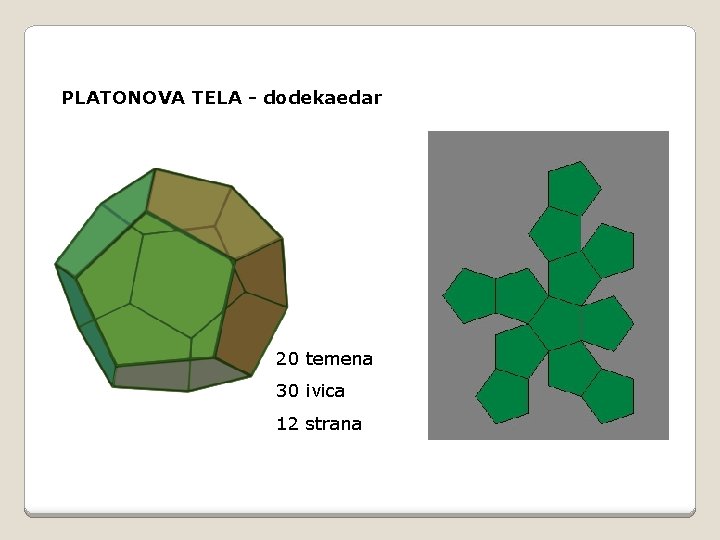
PLATONOVA TELA - dodekaedar 20 temena 30 ivica 12 strana

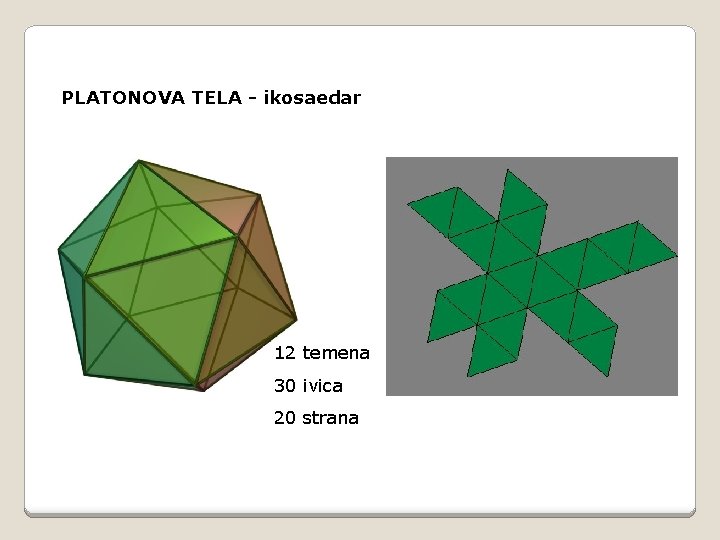
PLATONOVA TELA - ikosaedar 12 temena 30 ivica 20 strana

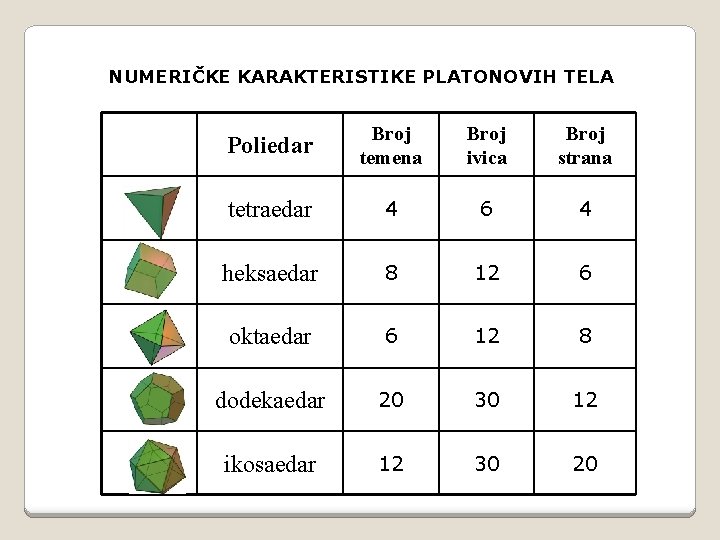
NUMERIČKE KARAKTERISTIKE PLATONOVIH TELA Poliedar Broj temena Broj ivica Broj strana tetraedar 4 6 4 heksaedar 8 12 6 oktaedar 6 12 8 dodekaedar 20 30 12 ikosaedar 12 30 20