POLIEDRI Anastazija Gajic Poliedar je deo prostora koji

POLIEDRI Anastazija Gajic

Poliedar je deo prostora koji je ogranicen mnogouglovima, pri cemu vaze sledeci uslovi 1. Svaka stranica bilo kog mnogougla je stranica jos jednog njemu susednog mnogougla. 2. Svaka dva susedna mnogougla pripadaju razlicitim ravnima. 3. Svaka dva nesusedna mnogougla se mogu povezati, nizom mnogouglova, takvim da su uzastopni clanovi susedni mnogouglovi. Poliedri dele prostor na dva dela. Jedan je zatvoren deo unutar mnogouglova, a drugi je spoljasnji deo izvan mnogouglova. Unija svih mnogouglova koji ogranicavaju polieder naziva se poliedarska povrs. Svaki od mnogouglova u poliedru naziva se strana poliedra

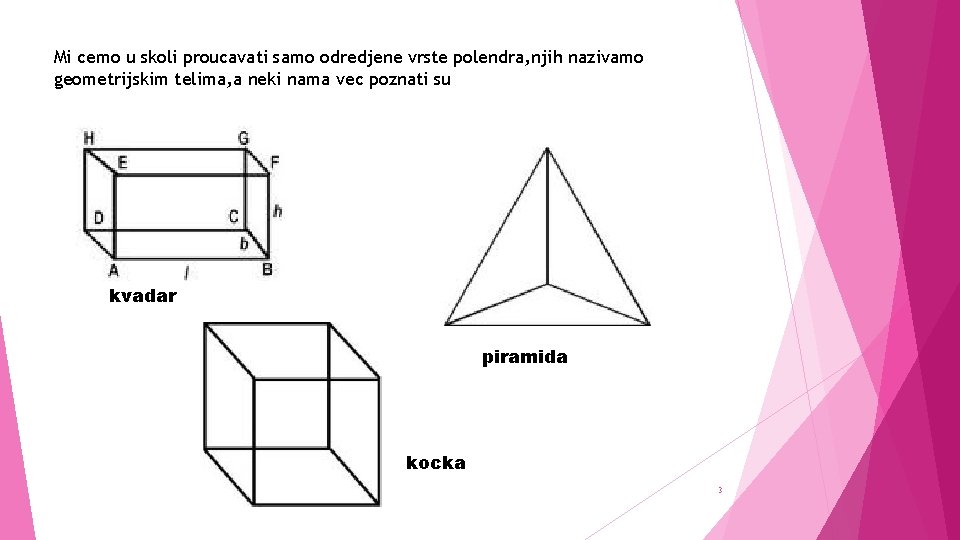
Mi cemo u skoli proucavati samo odredjene vrste polendra, njih nazivamo geometrijskim telima, a neki nama vec poznati su kvadar piramida kocka 3

Poliedri mogu biti konveksni i nekonveksni-konkavni. Poliedar je konveksan ukolika svaka duz koja spaja njegove dve proizvoljne tacke pripada tom polideru, u suprotnom slucaju poliedar je nekonveksan odnosno kovkavan. Коnveksni poliedri Коnveksni poliedar lezi samo sa jedne strane ravni svake svoje strane. Konveksni poliedar se moze predstaviti kao presek konacog broja poluprostora odredjenih ravnima njegovh strana. Regualni poliedri Poliedri cije su svе strane regularni podudarni mnogouglovi i ciji su svi rogljevi podudarni naziva se regularan poliedar.

Pravilni polideri su konveksni polideri cije su sve strane pravilni i medjusobno podudarni mnogouglovi i kod kojih iz svakog temena polazi isti broj ivica. Postoji samo pet pravilnih polidera. To su: teteadar ( sastoji se iz 4 јеdnakostranicna trougla) heksadar(kocka-sastoji se iz 6 kvadrata) оktaedar (sastoji se iz 8 јеdnakostranicnih trouglova) dodekaedar (sastoji se iz 12 pravilnih petouglova) iokosaedar (sastoji se 20 јеdnakostranicnih trouglova)

Оtkriveni su pre vise od 2000 godina I nazivaju ih Platonovim telima, po imenu starogrckog filozofa (427. p. n. e. -347. p. n. e. ), iako Platon nije otkrio ni jedno od ovih tela. Neki ove pravilne poliedre nayivaju I Pitagorinim telima (Pitagora 570. p. n. e. -495. p. n. e. ), jer je otkrio da su se jos Pitagorejci bavili ovim telima. Pitagorejci su bili ocarani pravilnim telima, ali I cinjenicom da pravilnih poligona ima beskonacno mnogo, a ptavilnih tela samo 5. (Dokaz da ih je samo 5 izveli su dosta kasnije mateaticari Rene Dekart i Leonardo Ojler). Iz nekog razloga, upucenost u telo nazvano dodekaedar, cinila im se opasnom. Ono je na misticki nacin dovodjeno u vezu sa kosmosom. Ostala cetiri tela poistovecivana su sa elementima koji cine svet: sa zemljom, vatrom, vazduhom i vodom. Zato se smatralo da ovaj „peti element“ ne treba otkrivati vec je valjalo obican svet drzati u ne znanju o dodokaedru. Cak je I Platon kompletno opisao cetiri pravilna tela, a za dodokaedar kaze: „Postoji I peti, Bog ga je upotrebio za svemir, oslikujuci na njmu likove (zodijaka).

Formule

KRAJ .