POLE TRAPEZU Wyprowadzenie wzoru Przykady Na pocztek Czworoktem

POLE TRAPEZU Wyprowadzenie wzoru. Przykłady.

Na początek: Czworokątem nazywamy część płaszczyzny ograniczonej łamaną zwyczajną zamkniętą o czterech bokach.

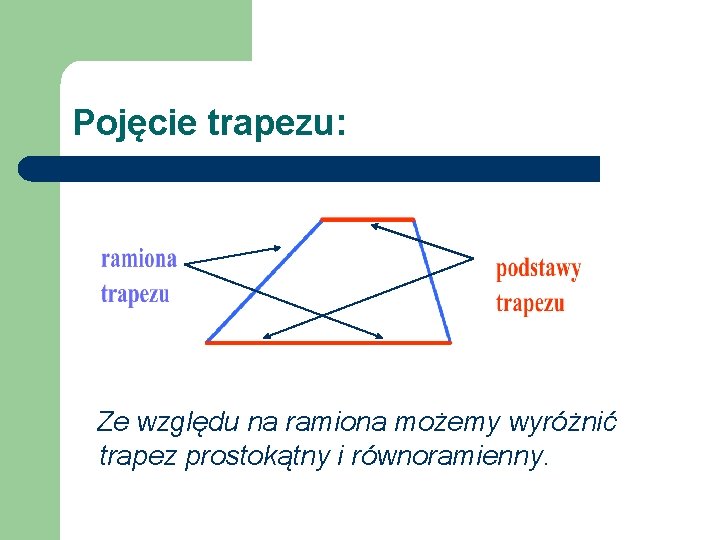
Dalej: l Czworokąt, który ma chociaż jedną parę boków równoległych nazywamy trapezem.

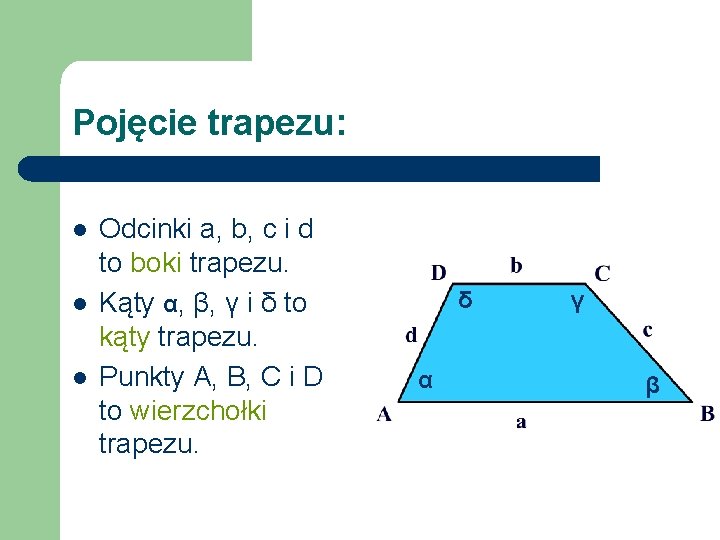
Pojęcie trapezu: l l l Odcinki a, b, c i d to boki trapezu. Kąty α, β, γ i δ to kąty trapezu. Punkty A, B, C i D to wierzchołki trapezu. δ α γ β

Pojęcie trapezu: Ze względu na ramiona możemy wyróżnić trapez prostokątny i równoramienny.

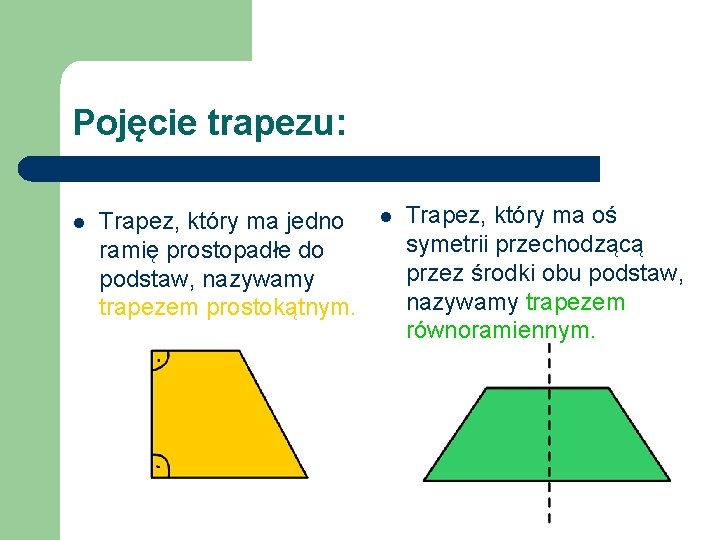
Pojęcie trapezu: l Trapez, który ma jedno ramię prostopadłe do podstaw, nazywamy trapezem prostokątnym. l Trapez, który ma oś symetrii przechodzącą przez środki obu podstaw, nazywamy trapezem równoramiennym.

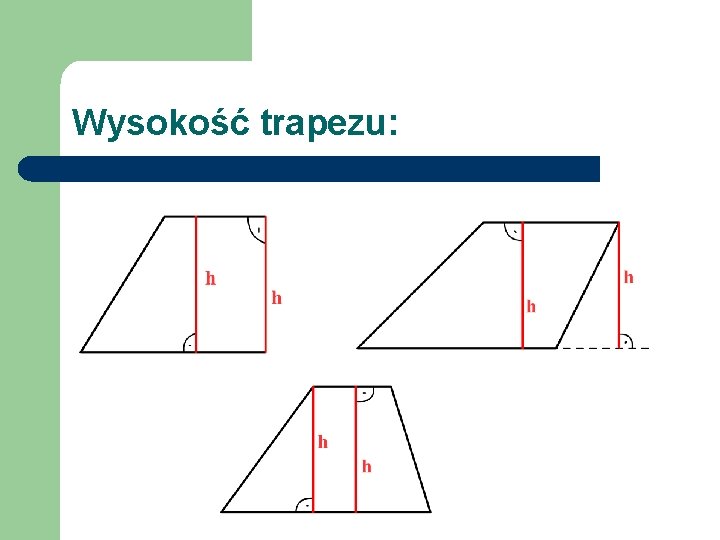
Wysokość trapezu: l l Wysokość trapezu, to odcinek łączący obie podstawy trapezu lub ich przedłużenia i prostopadły do nich. Wysokością trapezu nazywamy odległość między jego równoległymi bokami (odległość jest najkrótszym odcinkiem łączącym boki – jest prostopadły do boków).

Wysokość trapezu:

Równoważność trapezu i prostokąta. l Wiemy już, jak oblicza się pole prostokąta. l Czy potrafisz tak rozciąć dowolny trapez, aby z otrzymanych części powstał prostokąt?

POLE PROSTOKĄTA Przypomnijmy sobie jak oblicza się pole prostokąta? P=a • b Pole prostokąta równe jest iloczynowi długości jego boków prostopadłych do siebie.

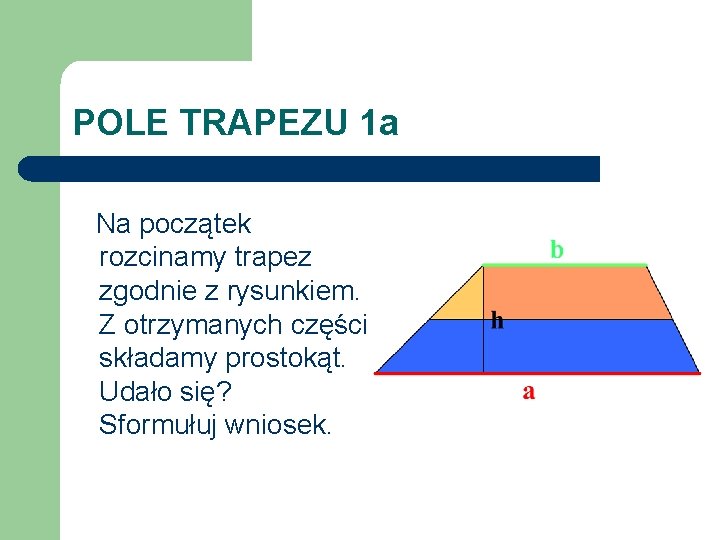
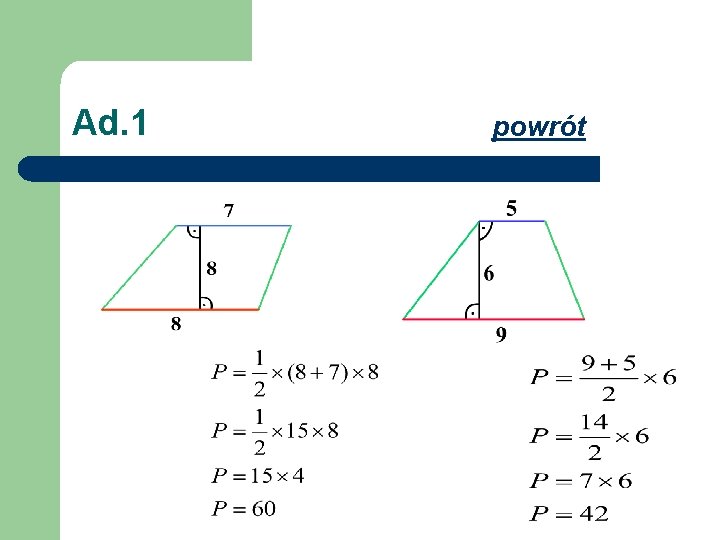
POLE TRAPEZU 1 a Na początek rozcinamy trapez zgodnie z rysunkiem. Z otrzymanych części składamy prostokąt. Udało się? Sformułuj wniosek.

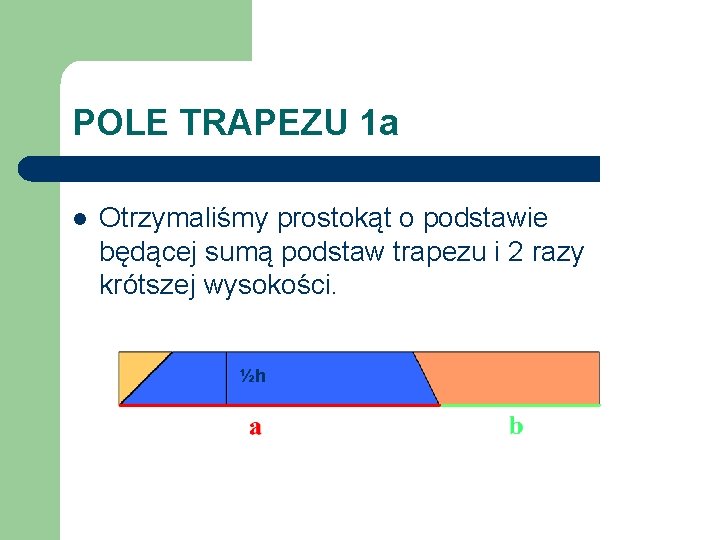
POLE TRAPEZU 1 a l Otrzymaliśmy prostokąt o podstawie będącej sumą podstaw trapezu i 2 razy krótszej wysokości. ½h

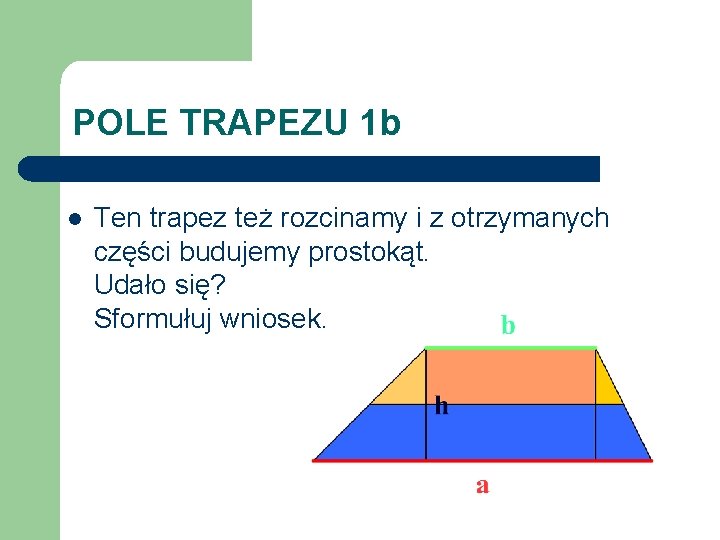
POLE TRAPEZU 1 b l Ten trapez też rozcinamy i z otrzymanych części budujemy prostokąt. Udało się? Sformułuj wniosek.

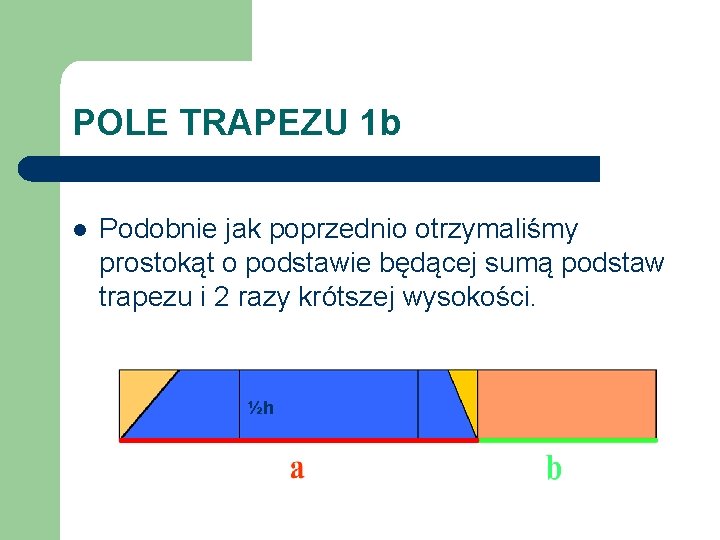
POLE TRAPEZU 1 b l Podobnie jak poprzednio otrzymaliśmy prostokąt o podstawie będącej sumą podstaw trapezu i 2 razy krótszej wysokości. ½h

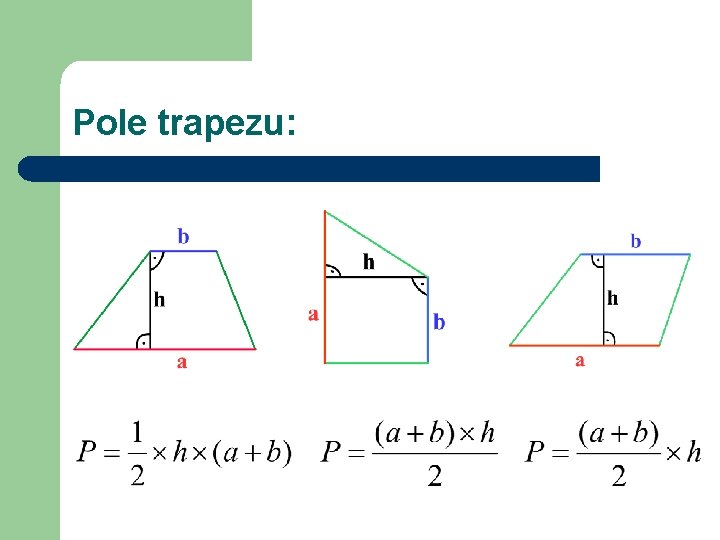
Wniosek: l Pole trapezu jest równe polu prostokąta o podstawie będącej sumą podstaw trapezu i 2 razy krótszej wysokości. l Zależność tę można przedstawić za pomocą wzoru:

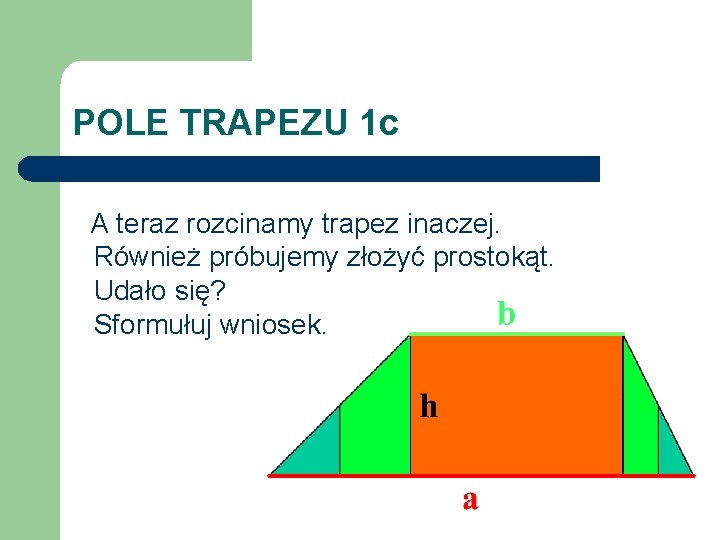
POLE TRAPEZU 1 c A teraz rozcinamy trapez inaczej. Również próbujemy złożyć prostokąt. Udało się? Sformułuj wniosek.

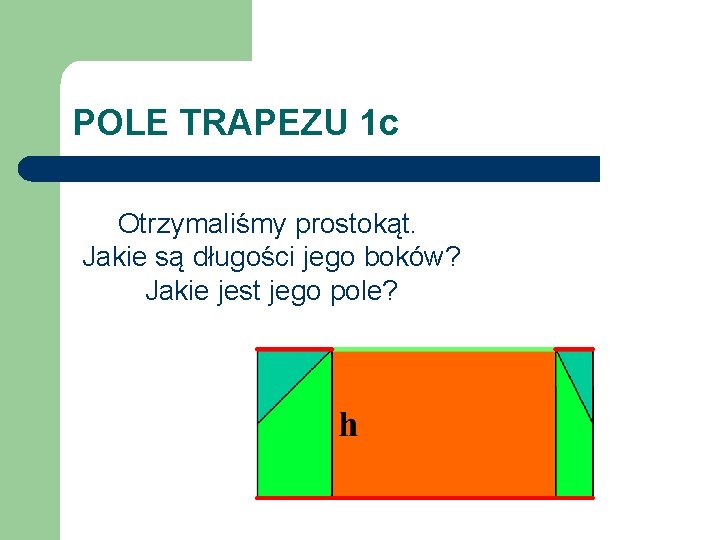
POLE TRAPEZU 1 c Otrzymaliśmy prostokąt. Jakie są długości jego boków? Jakie jest jego pole?

Równoważność trapezu i trójkąta. l Wiemy już, jak oblicza się pole trójkąta. l Czy potrafisz tak rozciąć dowolny trapez, aby z otrzymanych części powstał trójkąt?

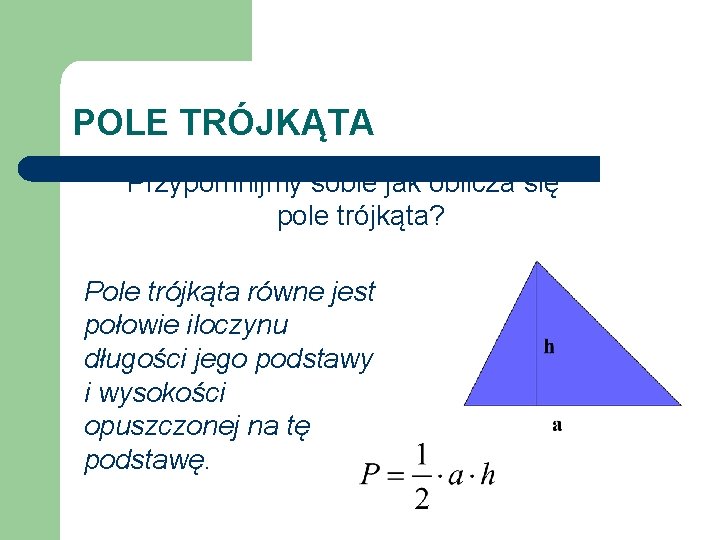
POLE TRÓJKĄTA Przypomnijmy sobie jak oblicza się pole trójkąta? Pole trójkąta równe jest połowie iloczynu długości jego podstawy i wysokości opuszczonej na tę podstawę.

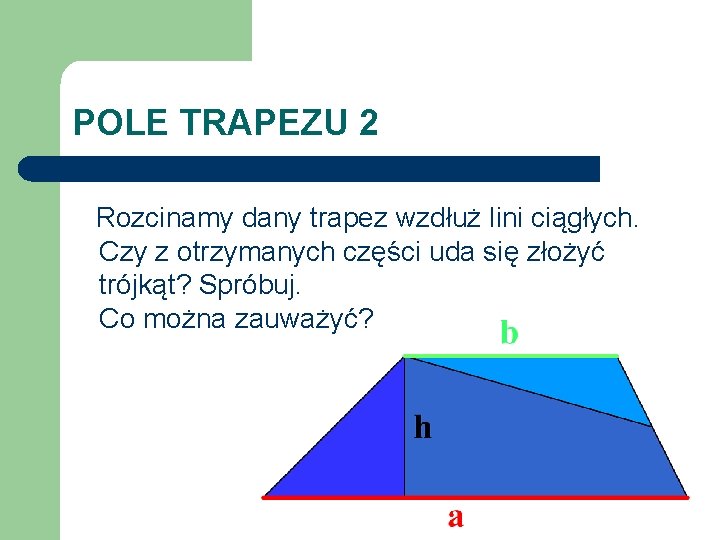
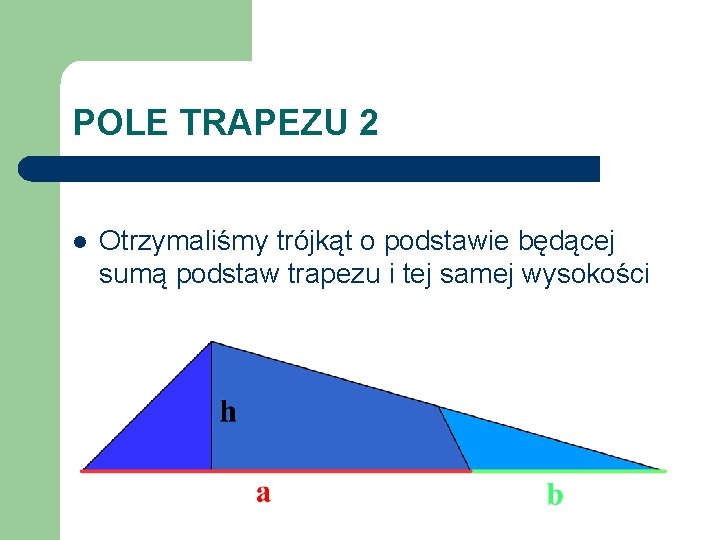
POLE TRAPEZU 2 Rozcinamy dany trapez wzdłuż lini ciągłych. Czy z otrzymanych części uda się złożyć trójkąt? Spróbuj. Co można zauważyć?

POLE TRAPEZU 2 l Otrzymaliśmy trójkąt o podstawie będącej sumą podstaw trapezu i tej samej wysokości

Wniosek: l Pole trapezu jest równe polu trójkąta o podstawie będącej sumą podstaw trapezu i tej samej wysokości. l Zależność tę można przedstawić za pomocą wzoru:

PODSUMOWANIE l l Można wykazać równoważność pola trapezu i prostokąta, jak i pola trapezu i trójkąta. Pole trapezu jest równe połowie iloczynu długości wysokości (h) oraz sumy długości jego podstaw (a, b), co można wyrazić wzorami:

Pole trapezu:

Zobaczmy to jeszcze raz l Pole trapezu 1 a l Pole trapezu 1 b l Pole trapezu 2

Obliczanie pola trapezu. Przykłady.

Przykłady: l l l 1. Oblicz pola narysowanych trapezów. 2. Oblicz pole trapezu o podstawach a i b oraz wysokości h: 3. Oblicz pole trapezu prostokątnego: UWAGA: Wysokością w trapezie prostokątnym jest ramię prostopadłe do obu podstaw. KONIEC

Ad. 1 powrót

Ad. 2 l Zad. 1 a = 8 cm b = 7 cm h = 4 cm powrót l Zad. 2 a = 9, 2 cm b = 8 cm h = 8 cm

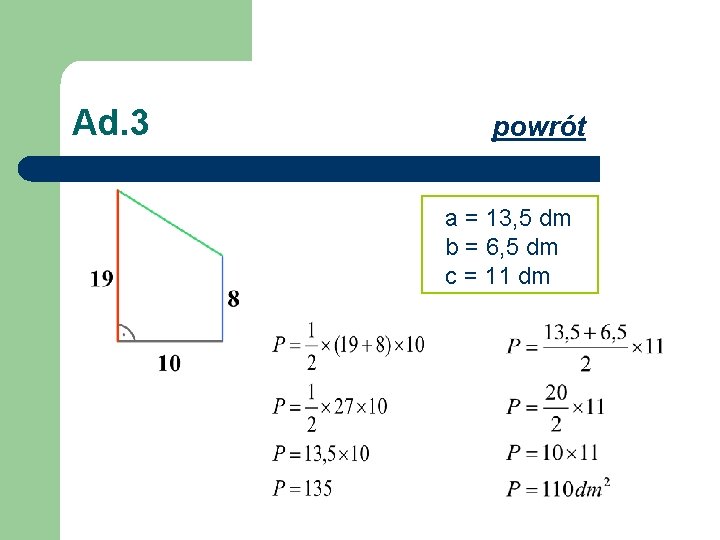
Ad. 3 powrót a = 13, 5 dm b = 6, 5 dm c = 11 dm

KONIEC POKAZU DZIĘKUJĘ I ZAPRASZAM NA KOLEJNĄ PREZENTACJĘ. Violetta Cymerys