POLAR COORDINATES DR SHILDNECK THE POLAR COORDINATE SYSTEM

POLAR COORDINATES DR. SHILDNECK

THE POLAR COORDINATE SYSTEM • The foundation of the polar coordinate system is a horizontal ray that extends to the right. • The ray is called the Polar Axis. • The endpoint of the ray is called the Pole. • A point P in the polar coordinate system is represented by the ordered pair (r, Ѳ). • r is a directed distance from the pole. • Ѳ is the angle from the polar axis to the line segment that passes from the pole to P. – The angle can be measured in either degrees or radians. – Positive angles are measured counterclockwise from the polar axis. – Negative angles are measured clockwise from the polar axis. • (r, Ѳ) are the polar coordinates of P. Ѳ r Pole Polar Axis

PLOTTING POINTS IN A POLAR COORDINATE SYSTEM • As a result of measuring distances and then rotating them, the polar coordinate system is made up of a set of concentric circles, set equal distances apart from one another, with the pole at their centers. • The distance between circles is (typically) one unit. • Typical polar graph papers include directional lines every 15 o (or π/2 radians). • The horizontal and vertical lines through the pole are the same axes as the x and y axes on rectangular systems.

PLOTTING POINTS IN A POLAR COORDINATE SYSTEM • r can be positive or negative. |r| = distance from the pole. • If r is positive, the point is IN the direction of the terminal side. • If r is negative, the point is in the OPPOSITE direction as the terminal side. • Ѳ is the angle of rotation. • When plotting the point (r, Ѳ), it is often easier to move in the opposite order. – Starting at the pole, rotate and look in the direction of Ѳ. – Apply r… • If r is positive, move that direction r steps.

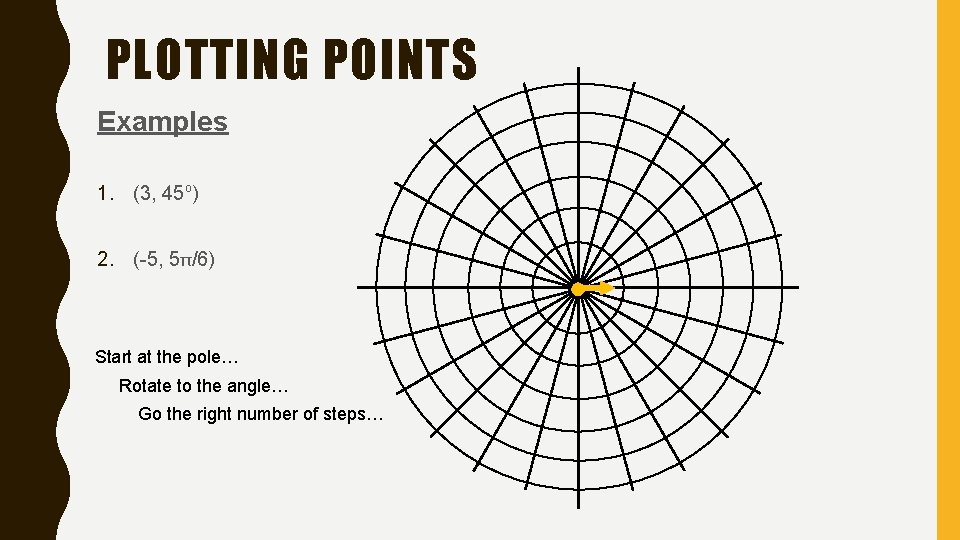
PLOTTING POINTS Examples 1. (3, 45 o) 2. (-5, 5π/6) Start at the pole… Rotate to the angle… Go the right number of steps…

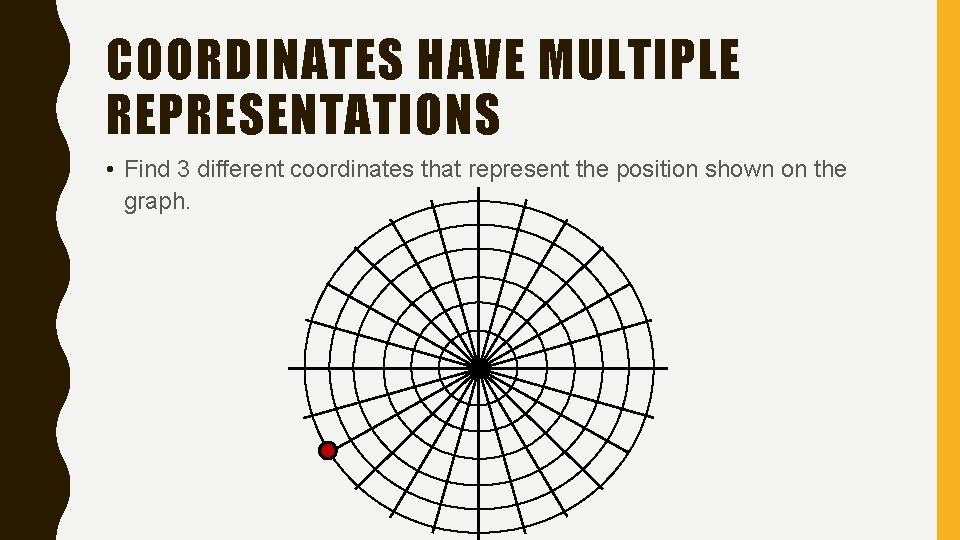
COORDINATES HAVE MULTIPLE REPRESENTATIONS • Since r can be positive or negative, and • Since Ѳ can rotate either direction. . . • Every point has infinitely different representations. – By changing the angle Ѳ by 360 degrees, we can use the same r-value with a different angle. – By changing the angle Ѳ by 180 degrees, we can use the opposite r-value with a different angle. If n is any integer, the point (r, Ѳ) can be represented as (r, Ѳ) = (r, Ѳ + 2πn) or (r, Ѳ) = (-r, Ѳ + π + 2πn)

COORDINATES HAVE MULTIPLE REPRESENTATIONS • Find 3 different coordinates that represent the position shown on the graph.

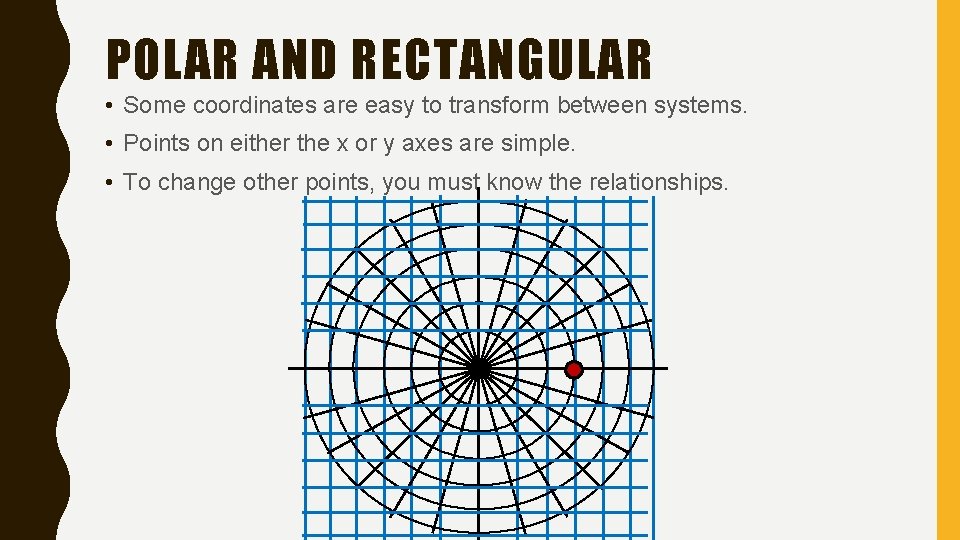
POLAR AND RECTANGULAR COORDINATES • The polar coordinate system represents the same locations that our Cartesian coordinate system does. • The only difference is how the position is indicated. • The origin in the rectangular system is the same as the pole in the polar. • Since the rectangular system is represented by horizontal (x) and vertical (y) movements based on the origin, and the polar system is represented by angles and “slanted” movements, there algebraic/trigonometric conversion formulas that describe the relationship between the two systems.

POLAR AND RECTANGULAR • Some coordinates are easy to transform between systems. • Points on either the x or y axes are simple. • To change other points, you must know the relationships.

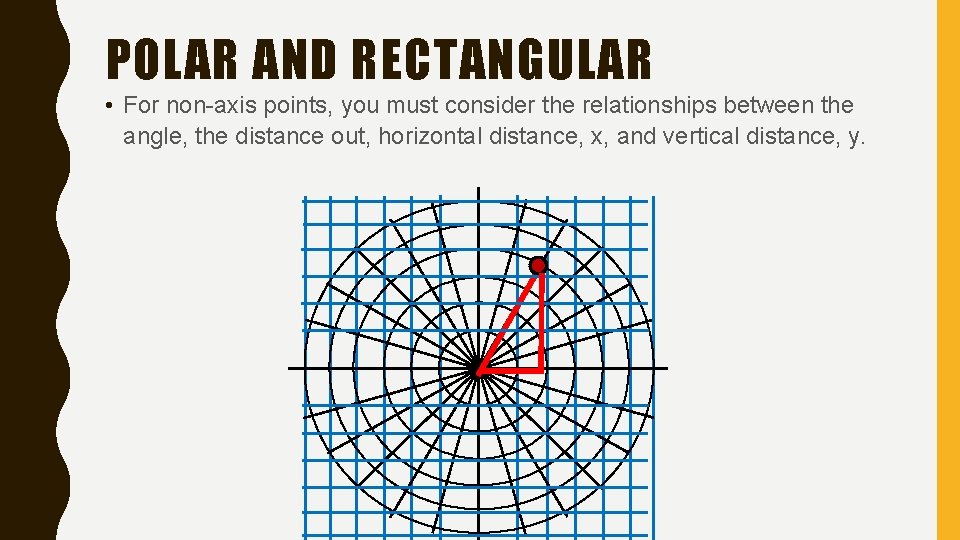
POLAR AND RECTANGULAR • For non-axis points, you must consider the relationships between the angle, the distance out, horizontal distance, x, and vertical distance, y.

POLAR AND RECTANGULAR COORDINATES • The relationship between the three distances (x, y, and r) is the Pythagorean theorem. • The relationship between the angle (Ѳ) and the x and y is the tangent.

POLAR AND RECTANGULAR COORDINATES • Convert the following polar coordinates to rectangular. • Convert the following rectangular coordinates to polar (nearest tenth degree).

POLAR EQUATIONS • A Polar Equation is an equation whose variables are r and theta. • There a number of different types of polar equations, but most are written with r in terms of theta. • Examples of polar equations include…

POLAR AND RECTANGULAR EQUATIONS • It is often easier to draw the graph of an equation in terms of polar coordinates rather than rectangular (and vice versa). • For this purpose, we need to be able to convert equations between systems. • Sometimes we can use the conversions for polar coordinates to help do this. But, most of the time, we need more “handy” formulas to transform equations. • These equations include our “typical” formulas for x and y (that we saw when working with vectors) in terms of the sine and cosine.

RECTANGULAR TO POLAR CONVERSIONS • Example 1

RECTANGULAR TO POLAR CONVERSIONS • Example 2

POLAR TO RECTANGULAR CONVERSIONS • Example 1

POLAR TO RECTANGULAR CONVERSIONS • Example 1

POLAR TO RECTANGULAR CONVERSIONS • Example 1

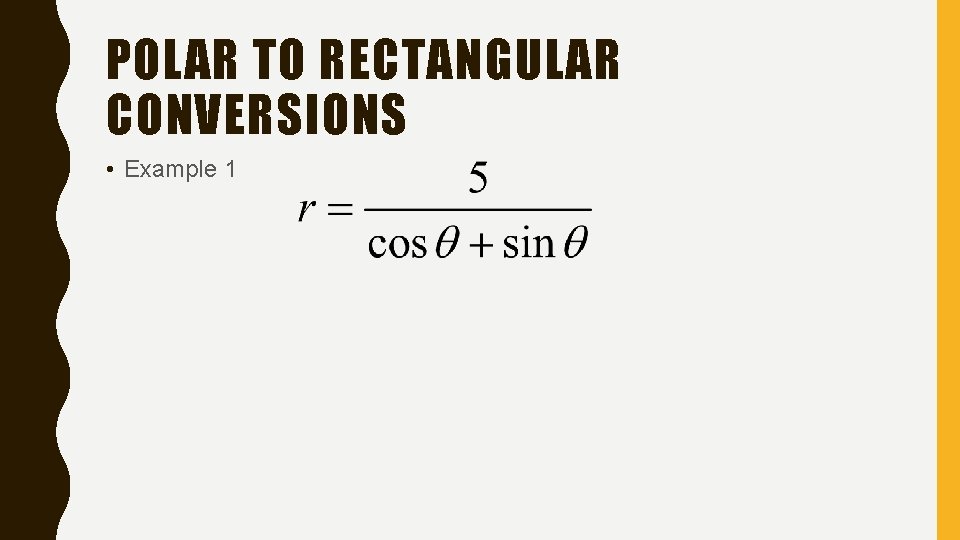
POLAR TO RECTANGULAR CONVERSIONS • Example 1

ASSIGNMENT 1 • Handout Textbook Page • #3, 9, 19, 21 , 23, 25, 31, 47, 51, 53, 55, 61, 73, 75, 77 -80 all