Poisson Surface Reconstruction Michael Kazhdan Matthew Bolitho Hugues

Poisson Surface Reconstruction Michael Kazhdan Matthew Bolitho Hugues Hoppe Johns Hopkins University Microsoft Research Presenter：Zhijie Wu

Outline Introduction Method Poisson Surface Reconstruction Result Conclusion Visual Computing Research Center (VCC)

Outline Introduction Poisson Surface Reconstruction Method Result Conclusion Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Background include point position and inward-facing normal Input Poisson Surface Reconstruction Output 4 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Related Work work 02 Global fitting methods work 01 [Greg Turk et. al 2002] Combinatorial structures [Ravikrishna Kolluri et. al 2004] work 04 work 03 Use a Poisson system to fit a 2. 5 D height field Local fitting methods [Diego Nehab et. al 05] [Brian Curless et. al 96] Poisson Surface Reconstruction 5 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Key concepts Indicator function An indicator function is a function defined on a set X that indicates membership of an element in a subset A of X, having the value 1 for all elements of A and the value 0 for all elements of X not in A. Poisson Surface Reconstruction 6 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Motivation and Key observation Intuitive illustration of Poisson reconstruction in 2 D Poisson Surface Reconstruction 7 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Motivation and Key observation Intuitive illustration of Poisson reconstruction in 2 D Poisson Surface Reconstruction 8 Visual Computing Research Center (VCC)

Outline Introduction Poisson Surface Reconstruction Method Results Conclusion Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Relationship A lemma about the gradient of the smoothed indicator function and the surface normal field indicator function of model M a smoothing filter Poisson Surface Reconstruction boundary of model M 10 the inward surface normal at p Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Relationship indicator function is equal to zero outside of Model and one inside it Divergence Theorem A similar argument shows that the y-, and z-components of the two sides are equal Poisson Surface Reconstruction 11 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Relationship approximate the integral exhibited in the front page with a discrete summation The area of the patch Poisson Surface Reconstruction 12 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Pipeline of Poisson Reconstruction step 02 ● Construct an octree step 04 ● express the vector field as a linear sum of node functions ● set up and solve the Poisson equation step 01 Poisson Surface Reconstruction ● extract an isosurface of the indicator function step 03 13 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Construct an octree • Motivation: – an accurate representation of the implicit function is only necessary near the reconstructed surface the use of an adaptive octree represent the implicit function Poisson Surface Reconstruction solve the Poisson system 14 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Construct an octree Finer nodes are associated with higher-frequency functions, and the function representation becomes more precise as we near the surface. Poisson Surface Reconstruction 15 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Define a space of functions For every node of octree o, set Fo to be the unit-integral “node function” centered about the node o and stretched by the size of o the center of node o Poisson Surface Reconstruction the width of node o 16 Visual Computing Research Center (VCC)

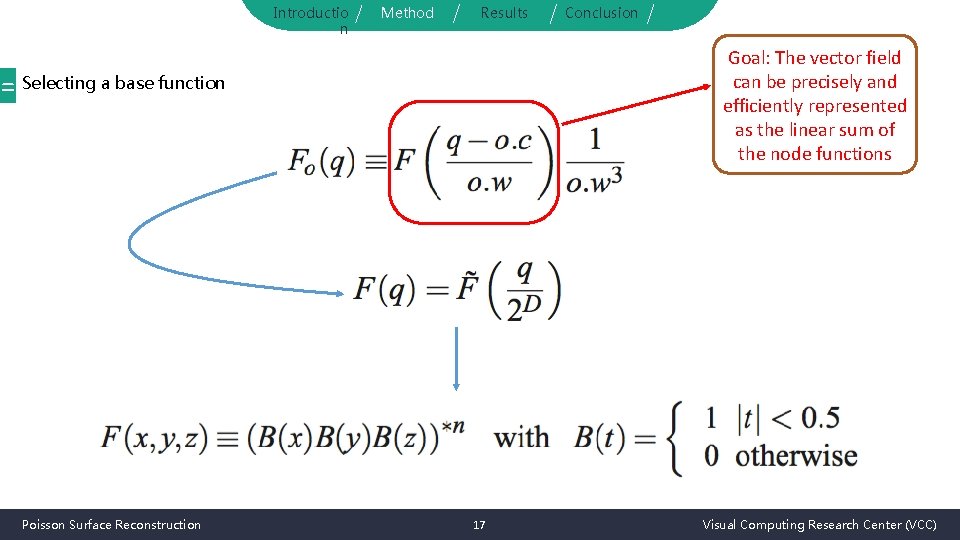
Introductio n Method Results Goal: The vector field can be precisely and efficiently represented as the linear sum of the node functions = Selecting a base function Poisson Surface Reconstruction Conclusion 17 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Vector Field Definition For higher precision, we use trilinear interpolation to distribute the sample across the eight nearest nodes the eight depth-D nodes closest to s. p Poisson Surface Reconstruction the trilinear interpolation weights 18 the inward surface normal at p Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Solve the Poisson Solution Since solving for and may not be in the space which and are in amounts to finding x satisfying such constraint Poisson Surface Reconstruction 19 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Isosurface Extraction • Operation Step: – first select an isovalue – then extract the corresponding isosurface from the computed indicator function using Marching Cubes Algorithms Poisson Surface Reconstruction 20 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Isosurface Extraction The output scalar function X, represented in an adaptive octree, is then isocontoured using an adaptive marching cubes to obtain the mesh. Poisson Surface Reconstruction 21 Visual Computing Research Center (VCC)

Outline Introduction Poisson Surface Reconstruction Method Results Conclusion Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Results Power Crust Robust Cocone Fast RBF MPU Poisson Surface Reconstruction 23 Visual Computing Research Center (VCC)

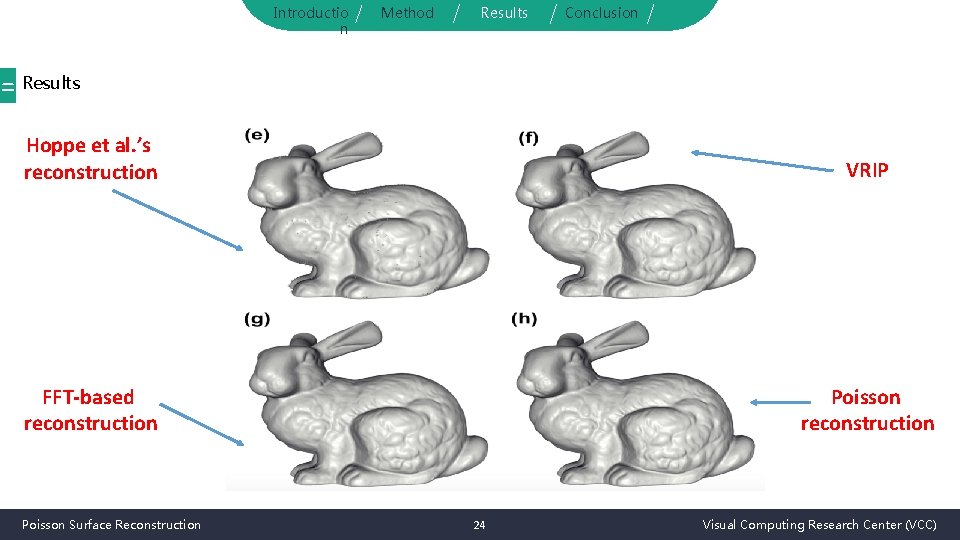
Introductio n Method Results Conclusion = Results Hoppe et al. ’s reconstruction VRIP FFT-based reconstruction Poisson Surface Reconstruction 24 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Results Reconstructions of a fragment of the Forma Urbis Romae tablet using VRIP and the Poisson solution VRIP Poisson Surface Reconstruction 25 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Results Reconstructions of the “Happy Buddha”model using VRIP and Poisson reconstruction Poisson solution VRIP Poisson Surface Reconstruction 26 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Results Reconstructions of the left eye of the David model using FFT and Poisson reconstruction Points from scans of the left eye of the David model Poisson Surface Reconstruction using the fixedresolution FFT approach 27 Poisson reconstruction Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Results Several images of the reconstruction of the head of Michelangelo’s David, obtained running our algorithm with a maximum tree depth of 11. Poisson Surface Reconstruction 28 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Results Several images of the reconstruction of the head of Michelangelo’s David, obtained running our algorithm with a maximum tree depth of 11. Poisson Surface Reconstruction 29 Visual Computing Research Center (VCC)

Introductio n = Comparison Method Results Conclusion in megabytes in seconds The running time, the peak memory usage, and the number of triangles in the reconstructed surface of the Stanford Bunny generated by the different methods Poisson Surface Reconstruction 30 Visual Computing Research Center (VCC)

Outline Introduction Poisson Surface Reconstruction Method Results Conclusion Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Conclusion The key challenge of Reconstruction How to accurately compute the indicator function from the samples 1 2 The goal of this method The goal is to reconstruct a watertight, triangulated approximation to the surface The key idea The key insight is that there is an integral relationship between oriented points sampled from the surface of a model and the indicator function of the model Poisson Surface Reconstruction 3 32 Visual Computing Research Center (VCC)

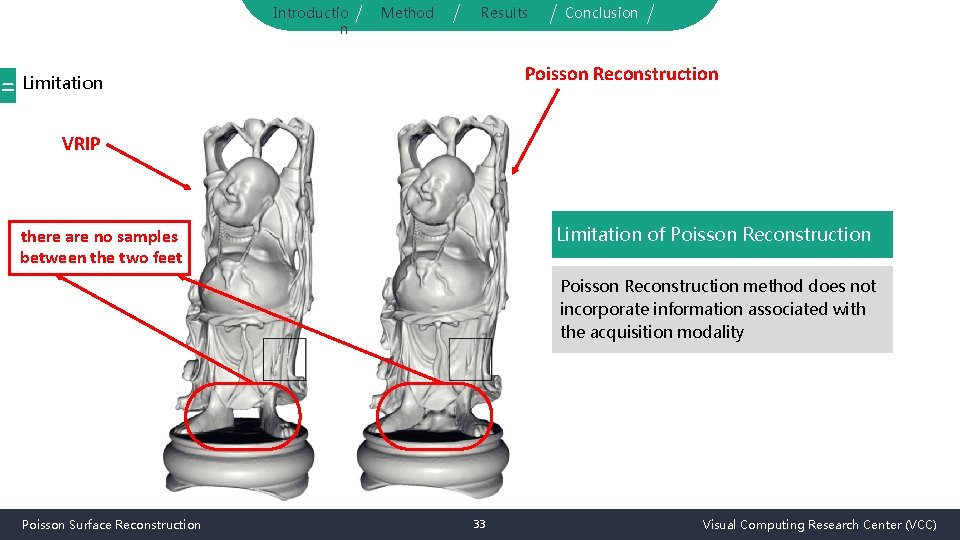
Introductio n Method Results Conclusion Poisson Reconstruction = Limitation VRIP Limitation of Poisson Reconstruction there are no samples between the two feet Poisson Reconstruction method does not incorporate information associated with the acquisition modality Poisson Surface Reconstruction 33 Visual Computing Research Center (VCC)

Introductio n Method Results Conclusion = Advantages of Poisson Reconstruction Advantage 01 Advantage 02 Advantage 03 Advantage 04 Be able to create very smooth surfaces that robustly approximate noisy data The solution of it can reduce to a wellconditioned sparse linear system Spurious surface sheets away from implicit function samples may seldom arise Poisson Reconstruction has strong resilience in the presence of imperfect data Poisson Surface Reconstruction 34 Visual Computing Research Center (VCC)

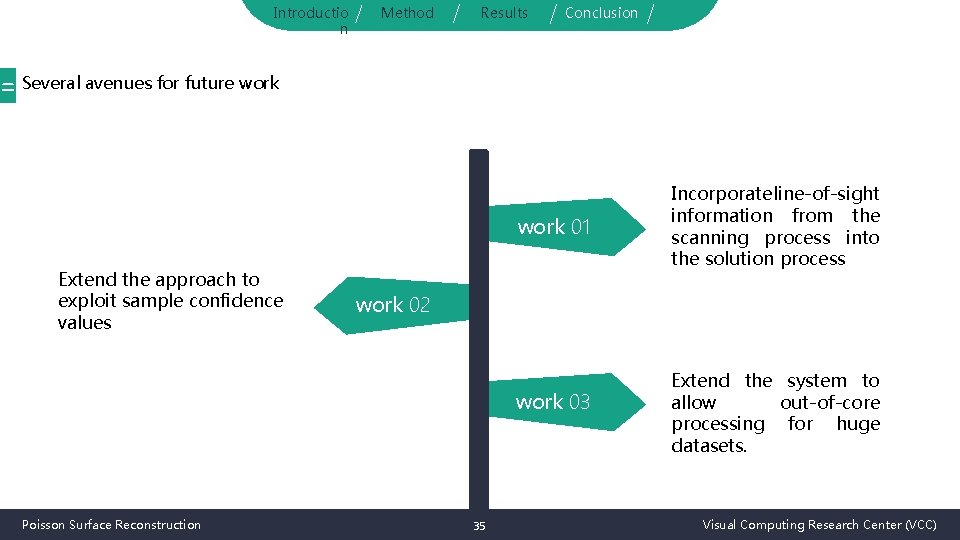
Introductio n Method Results Conclusion = Several avenues for future work 01 Extend the approach to exploit sample confidence values work 02 work 03 Poisson Surface Reconstruction Incorporate line-of-sight information from the scanning process into the solution process 35 Extend the system to allow out-of-core processing for huge datasets. Visual Computing Research Center (VCC)

Thank you! Presenter：Zhijie Wu Instructor：Ruizhen Hu

Q/A Question: There are so many data structures, such as K-D tree why do we use the Octree? Does Octree have some special advantages? Answer: Of course, there are some data structures used widely in computer graphics and computer vision and they have their own advantages in some specific fields. For example, we often use k-d tree to do something like searching neighbours in k-dimensions. But the octree is often used to discretize space, data partition storage and data search in 3 D space. And in this paper, we only want to discretize the 3 D space for further processing with an octree. So for efficiency, it’s better to use octree than k-d tree. Poisson Surface Reconstruction 37 Visual Computing Research Center (VCC)

Q/A Question: There is a smoothing filter in page 10, so why we use a Gaussian as the target filter? Answer: Well, in my opinion, when we choose the filter, we want the filter to satisfy two conditions. On the one hand, it should be sufficiently narrow so that we do not over-smooth the data. And on the other hand, it should be wide enough so that the integral over the patch can be well approximated by the value at the sample point and scaled by the patch area. And a good choice of filter that strike these two requirements is a Gaussian and its variance is on the order of the sampling resolution. Poisson Surface Reconstruction 38 Visual Computing Research Center (VCC)

Q/A Question: When we try to express the vector field as a linear sum of functions, why not just use basis function at the finest level but represent it as linear combinations of nodal basis functions across all levels? Answer: Uh, because the space is adaptive, not all coarse functions can be represented as a linear combination of finer functions. Thus, the functions we consider will be represented as linear combinations of nodal basis functions across all levels, not just the basis functions at the finest level. Poisson Surface Reconstruction 39 Visual Computing Research Center (VCC)

Q/A Question: Is the vector field or gradients appearing in this work a tensor? Answer: Yes, of course, a first rank tensor they are. Question: Can Poisson System reconstruct a sharp edge? Answer: Uh, it depends on how you define the sharp edges. In general, we say that the Poisson System create a mesh of model with a watertight and smooth surface. But in fact, the Poisson reconstruction method is independent of view direction, so it sometimes can accurately reconstructs some sharp creases in some models. Poisson Surface Reconstruction 40 Visual Computing Research Center (VCC)

Q/A Question: Can you explain in detail how the maximum octree depth influence the reconstruction result? As we can see in the paper, Poisson Reconstruction Method can create a higher-quality mesh with a larger octree depth. Answer: In this work, the author use the octree data structure to discretize the 3 D space. If given a larger octree depth, we get a finer partition of the space. So the maximum octree depth corresponds to the sampling width. We get a smaller sampling width with a larger maximum tree depth. When constructing the octree, we put the point sample into a leaf node at the maximum tree depth. So we can capture more detail of the model with a larger octree maximum depth. Poisson Surface Reconstruction 41 Visual Computing Research Center (VCC)

Q/A Question: In page 16, why should we select the base function and do this carefully? Answer: Well, as the content showed in page 17, we want to achieve a goal that the vector field can be precisely and efficiently represented as the linear sum of the node functions. And the formula in page 12 display the requirement we must meet if we want to meet the goal. So we must choose a right base function. Poisson Surface Reconstruction 42 Visual Computing Research Center (VCC)

Q/A Question: In page 3 of the paper, the author says that the vector field is generally not integrable, so why it is not integrable? Answer: As you can see, you must be clear about the conditions why a function can be integrable over certain domains. And one of the conditions is that the definition domain must be continuous. But the vector field here is discrete so it is not integrable. Poisson Surface Reconstruction 43 Visual Computing Research Center (VCC)

Q/A Question: In page 10, can you explain how to establish the relationship between the gradients and the inward-facing normal with more detail again? Answer: Well, the key idea of this paper is that there is a relationship between the gradients of the indicator function and the inward-facing normal. And the lemma I showed before explains the relationship exactly. And as the derivation of this lemma shows, the last equality, which follows from the Divergence Theorem associate the gradients of the indicator function to the inward-facing normal. Although it is only proofed with the x-components, but we can get the similar equality with y-components and z-components. So with the help of Divergence Theorem, the gradients of indicator function are linked with the inward-facing normal. Poisson Surface Reconstruction 44 Visual Computing Research Center (VCC)

Q/A Question: In page 10, why should the indicator function convolve with the smoothing filter? Can you explain it more clearly? Answer: In fact, I think there are two purposes to do so. The first one is that there are maybe a lot of noise data among all the input data. So we must filter the noise and then try to get a clean output. And the second purpose is that the indicator function is piecewise constant function, so explicit computation of its gradient field would result in a vector field with unbounded values at the surface boundary. So to avoid this, we must convolve the indicator function with a smoothing function and consider the gradient field of the smoothed function. Poisson Surface Reconstruction 45 Visual Computing Research Center (VCC)