Poisson Process Review Session 2 EE 384 X

Poisson Process Review Session 2 EE 384 X Winter 2006 EE 384 x 1

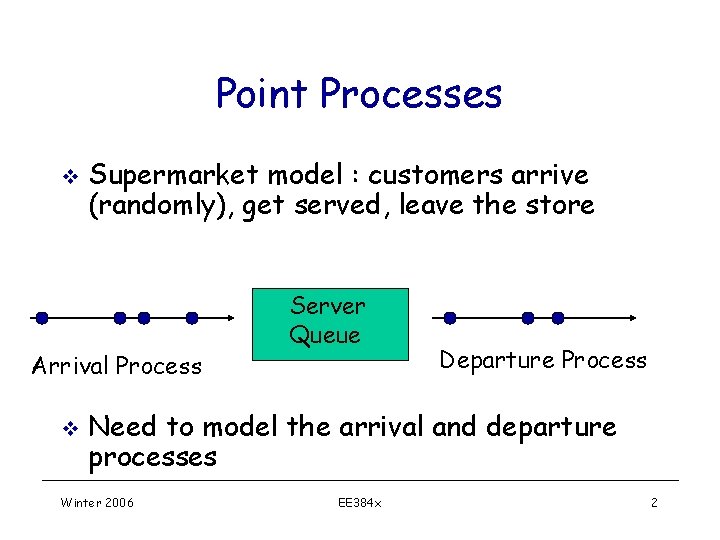
Point Processes v Supermarket model : customers arrive (randomly), get served, leave the store Arrival Process v Server Queue Departure Process Need to model the arrival and departure processes Winter 2006 EE 384 x 2

What does Poisson Process model? Start time of Phone calls in Palo Alto v Session initiation times (ftp/web servers) v Number of radioactive emissions (or photons) v Fusing of light bulbs, number of accidents v Historically, used to model packets (massages) arriving at a network switch v Ø (In Kleinrock’s Ph. D thesis, MIT 1964) Winter 2006 EE 384 x 3

Properties Say there has been 100 calls in an hour in Palo Alto v We expect that : v Ø Ø Ø v The start time of each call is independent of the others The start time of each call is uniformly distributed over the one hour The probability of getting two calls at exactly the same time is zero Poisson Process has the above properties Winter 2006 EE 384 x 4

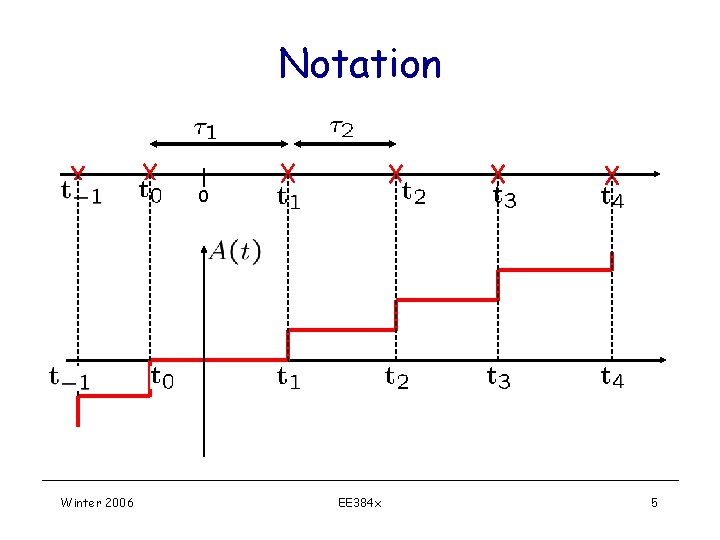
Notation 0 Winter 2006 EE 384 x 5

Notation v v A(t) : Number of points in (0, t] A(s, t) : Number of points in (s, t] v Arrival points : v Inter-arrival times: Winter 2006 EE 384 x 6

Poisson Process- Definition v A(0)=0 and each jump is of unit magnitude v Number of arrivals in disjoint intervals are independent Ø v For any the random variables independent. are Number of arrivals in any interval of length t is distributed Poisson(lt) Winter 2006 EE 384 x 7

Basic Properties Winter 2006 EE 384 x 8

Stationary Increments v The number of arrivals in (t, t+t] does not depend on t Winter 2006 EE 384 x 9

Orderliness v v The probability of two or more arrivals in an interval of length t gets small as Arrivals occur “one at a time” Winter 2006 EE 384 x 10

Poisson Rate v v Probability of one arrival in a short interval is (approx) proportional to interval length Poisson process is like a continuous version of Bernoulli IID Winter 2006 EE 384 x 11

Additional Properties Winter 2006 EE 384 x 12

Inter-arrival times v Inter-arrival times are Exponential(l) and independent of each other 0 Winter 2006 EE 384 x 13

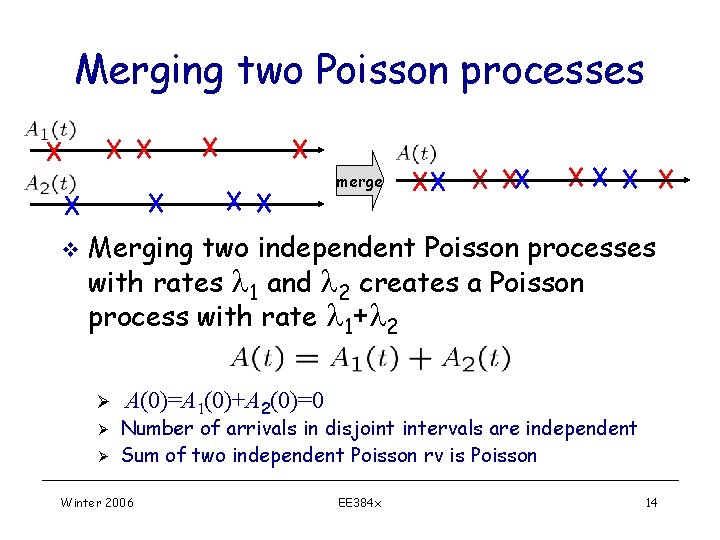
Merging two Poisson processes merge v Merging two independent Poisson processes with rates l 1 and l 2 creates a Poisson process with rate l 1+l 2 Ø Ø Ø A(0)=A 1(0)+A 2(0)=0 Number of arrivals in disjoint intervals are independent Sum of two independent Poisson rv is Poisson Winter 2006 EE 384 x 14

Sum of two Poisson rv v Characteristic function: v So Winter 2006 EE 384 x 15

Splitting a Poisson process : Poisson process with rate l Split v For each point toss a coin (with bias p): Ø Ø With probability p the point goes to A 1(t) With probability 1 -p the point goes to A 2(t) v A 1(t) and A 2(t) are two independent Poisson processes with rates Winter 2006 EE 384 x 16

proof v Define A 1(t) and A 2(t) such that: Ø v A 1(0)=0 A 2(0)=0 Number of points in disjoint intervals are independent for A 1(t) and A 2(t) Ø They depend on number of points in disjoint intervals of A(t) v Need to show that number of points of A 1 and A 2 in an interval of size t are independent Poisson(l 1 t) and Poisson(l 2 t) Winter 2006 EE 384 x 17

Dividing a Poisson rv Winter 2006 EE 384 x 18

Dividing a Poisson rv (cont) v So Winter 2006 EE 384 x 19

Uniformity of arrival times v Given that there are n points in [0, t], the unordered arrival times are uniformly distributed and independent of each other. Unordered variables 0 Ordered variables Winter 2006 EE 384 x 20

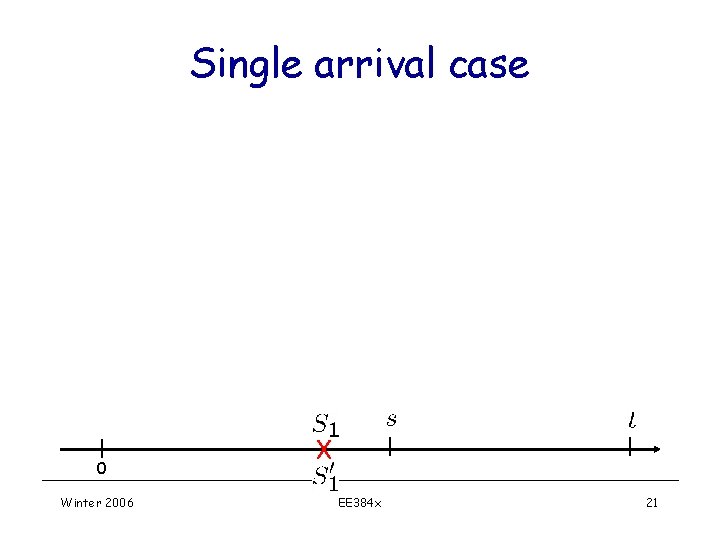
Single arrival case 0 Winter 2006 EE 384 x 21

General case v It is the n order statistics of uniform distribution. Winter 2006 EE 384 x 22