Poisson distribution as an approximation to the Example

Poisson distribution as an approximation to the Example Binomial distribution 10000 eggs are placed in a box. On the average, 0. 6% of the eggs break when they arrive at a supermarket. Find the probability that in a box exactly 50 eggs were broken. Let X = Number of eggs were broken. X ~ B ( 10, 000 , 0. 006 ) = 10000 (0. 006) = 60 X ~ Po ( 60 ) P ( X = 50 ) = 0. 0233 Example 2 : The probability that an individual in a country owns a motorbike is 0. 5. If 1000 individuals choose at a random, find the probability that exactly 500 of them own a motorbike. Let X = Number of individuals own a motorbike. X ~ B ( 1000 , 0. 5 ) 1. n is 2. p is big ( n ≥ 50 ) small ( p < 0. 1 ) Poisson approximation NOT suitable

Normal distribution as an approximation to the Binomial distribution 1. n is big ( n > 30 ) As a guide, np ≥ 5 and nq ≥ 5 2. p ≈ 0. 5 np = X~B(n, p) ( Discrete ) = 2 = nnp pq X ~ Po ( ) ( Discrete ) ( p < 0. 1 ) X ~ N ( , 2 ) ( p ≈ 0. 5 ) ( Continuous ) Normal Distribution ( Continuous random variable ) used as an approximation for Binomial Distribution (Discrete random variable) Continuity Correction

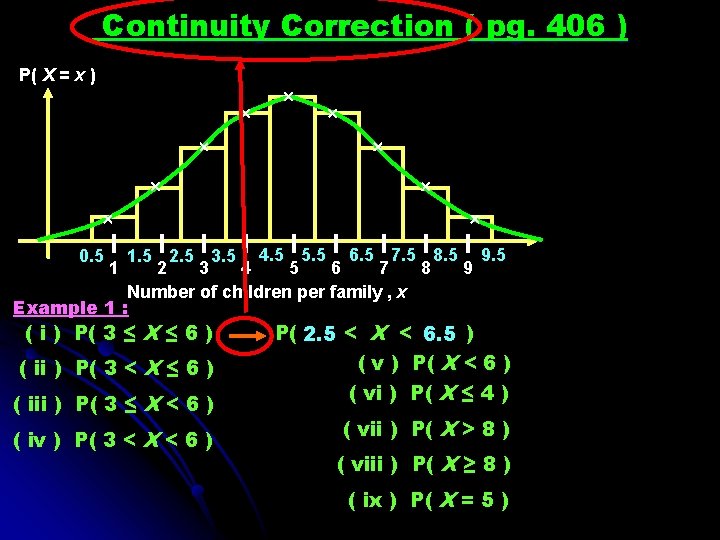
Continuity Correction ( pg. 406 ) P( X = x ) 1. 5 2. 5 3. 5 4. 5 5. 5 6. 5 7. 5 8. 5 9. 5 2 3 4 5 6 7 8 9 Number of children per family , x Example 1 : 0. 5 1 ( i ) P( 3 ≤ X ≤ 6 ) ( ii ) P( 3 < X ≤ 6 ) ( iii ) P( 3 ≤ X < 6 ) ( iv ) P( 3 < X < 6 ) P( 2. 5 < X < 6. 5 ) ( v ) P( X < 6 ) ( vi ) P( X ≤ 4 ) ( vii ) P( X > 8 ) ( viii ) P( X ≥ 8 ) ( ix ) P( X = 5 )

Example 2 : The probability that an individual in a country owns a motorbike is 0. 5. If 1000 individuals choose at a random, find the probability that exactly 500 of them own a motorbike. Let X = Number of individuals own a motorbike. X ~ B ( 1000 , 0. 5 ) = np = 1000 x 0. 5 = 500 2 = npq = 1000 x 0. 5 = 250 X ~ N ( 500 , 250 ) P ( X = 500 ) P( 499. 5 < X < 500. 5 ) = P( - 0. 0316 < Z < 0. 0316 ) = 0. 0252 Standardizing

Example 3 : Find the probability of obtaining between 4 to 6 ‘heads’ inclusive when a fair coin is tossed 16 times using the (a) binomial distribution , (b) normal distribution. Let X = Number of ‘heads’ obtained. X ~ B ( 16 , 0. 5 ) ( a ) P( 4 ≤ X ≤ 6 ) = P ( X = 4 ) +P ( X = 5 ) + P ( X = 6 ) = 16 C 4 (0. 5)12 + 16 C 5 (0. 5)11 + = 0. 2166 16 C 6 (0. 5)10 = np = 16 x 0. 5 = 8 2 = npq = 16 x 0. 5 = 4 (b) X~N(8, 4) ( a ) P( 4 ≤ X ≤ 6 ) P( 3. 5 < X < 6. 5 ) = P( - 2. 25 < Z < - 0. 75 ) = 0. 2144

STPM 2005 QUESTION 7 The mass of a small loaf of bread produced in a bakery may be modelled by a normal random variable with mean 303 g and standard deviation 4 g. Find the probability that a randomly chosen loaf has a mass between 295 g and 305 g. Answer (i) [3 marks] 0. 6687 STPM 2006 QUESTION 10 The probability that a heart patient survives after surgery in a country is 0. 85. (i) Find the probability that, out of five randomly chosen heart patient undergoing surgery, four survive. [3 marks] (ii) Using a suitable approximate distribution, find the probability that more than 160 survive after surgery in a random sample of 200 heart patients. [6 marks] Answer (i) 0. 3915 (ii) 0. 97

Exercise 8. 11 pg. 408 Q. 1 – 11 Revision Exercise pg. 412 Q. 14 – 38