Points to Remember The graphs of all functions

Points to Remember The graphs of all functions cut the x-axis where y = 0 The graphs of all functions cut the y-axis where x = 0

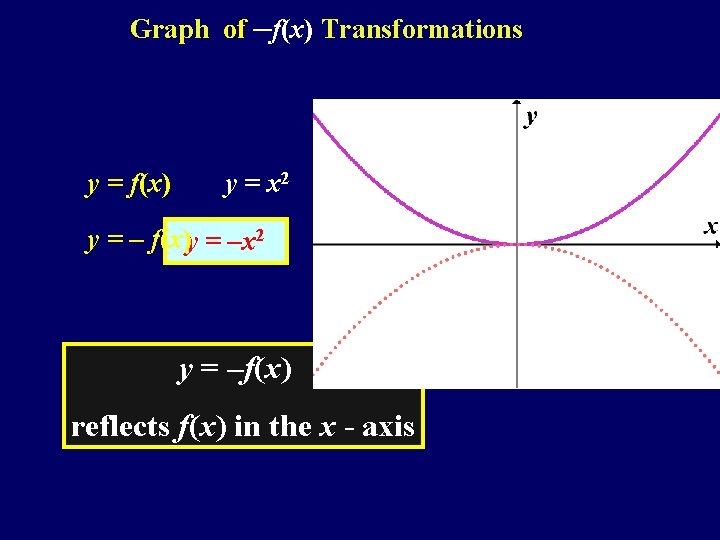
Graph of –f(x) Transformations y = f(x) y = x 2 y = – f(x)y = –x 2 y = –f(x) reflects f(x) in the x - axis

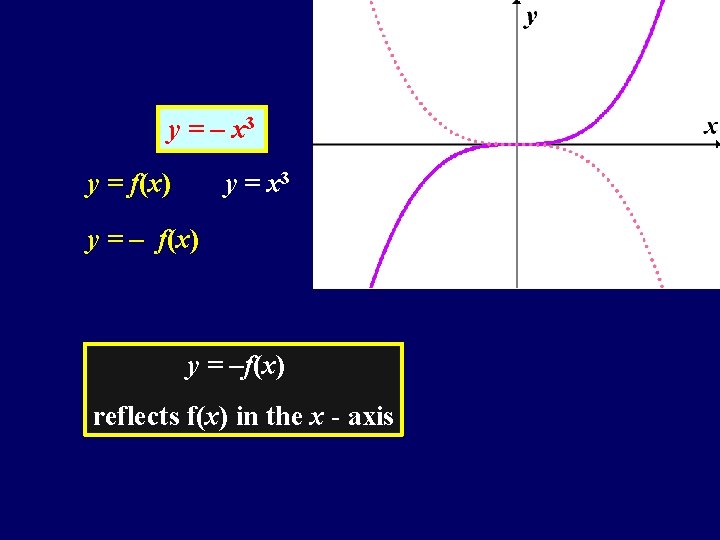
y = – x 3 y = f(x) y = x 3 y = – f(x) y = –f(x) reflects f(x) in the x - axis

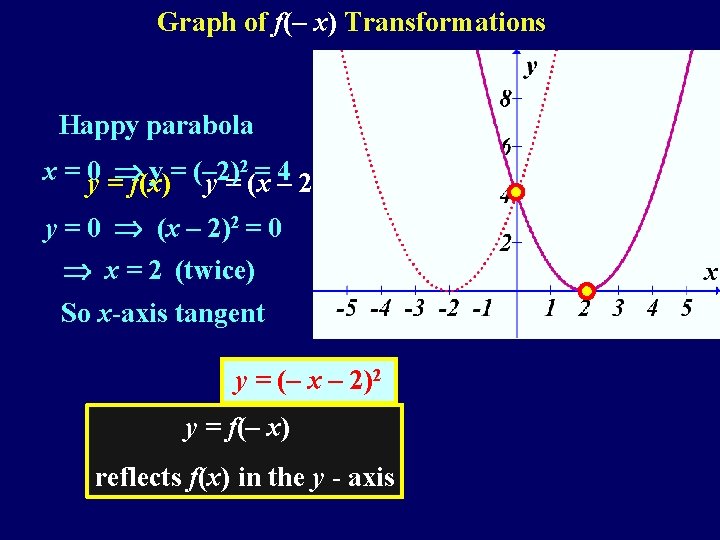
Graph of f(– x) Transformations Happy parabola 2= 4 x = 0 y = f(x) y = (– 2) y = (x – 2)2 y = f(– x ) y = 0 (x – 2)2 = 0 x = 2 (twice) So x-axis tangent y = (– x – 2)2 y = f(– x) reflects f(x) in the y - axis

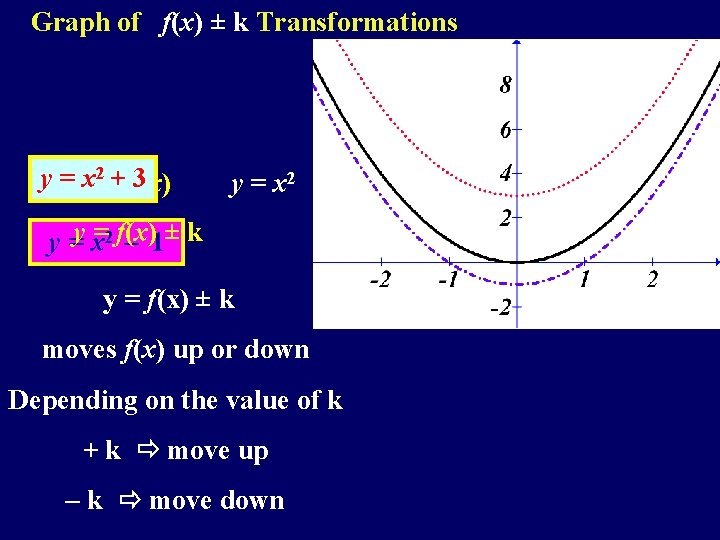
Graph of f(x) ± k Transformations y = xy 2 =+ f(x) 3 y = x 2 y =y x=2 f(x) – 1± k y = f(x) ± k moves f(x) up or down Depending on the value of k + k move up – k move down

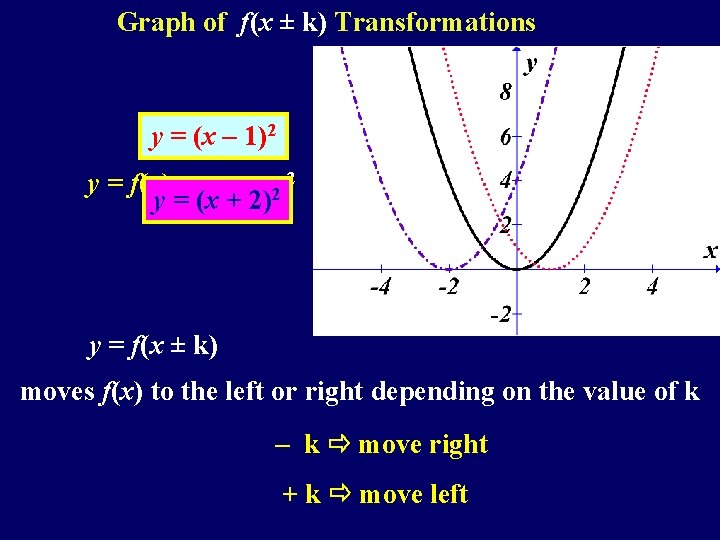
Graph of f(x ± k) Transformations y = (x – 1)2 y = f(x) y = 2 x 2 y = (x + 2) y = f(x ± k) moves f(x) to the left or right depending on the value of k – k move right + k move left

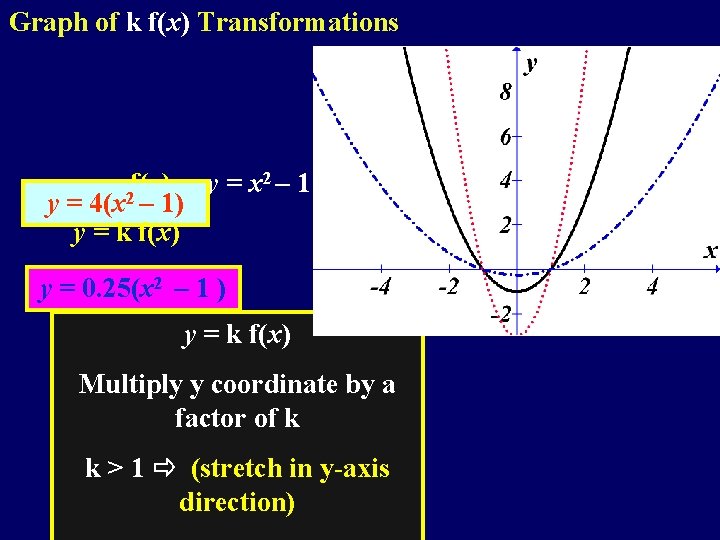
Graph of k f(x) Transformations y = 2 f(x) y = x 2 – 1 y = 4(x – 1) y = k f(x) y = 0. 25(x 2 – 1 ) y = k f(x) Multiply y coordinate by a factor of k k > 1 (stretch in y-axis direction)

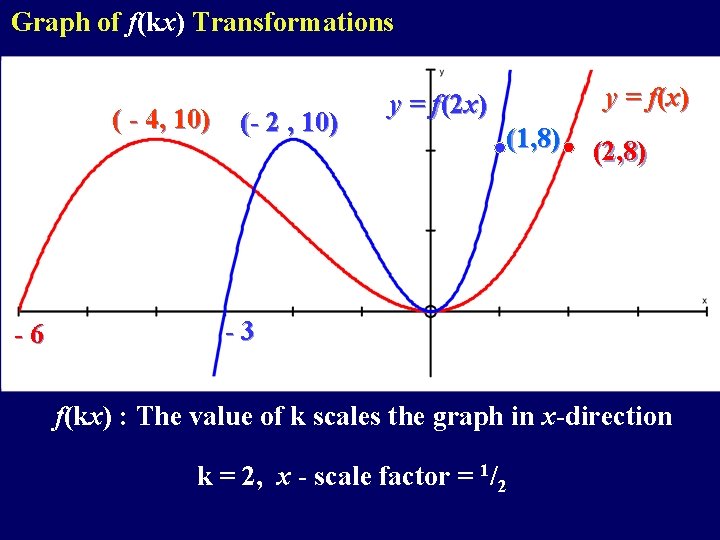
Graph of f(kx) Transformations (( -- 4, 4, 10) (- 2 , 10) -6 yy == ff((xx)) y = f(2 x) (1, 8) (2, 8) -3 f(kx) : The value of k scales the graph in x-direction k = 2, x - scale factor = 1/2

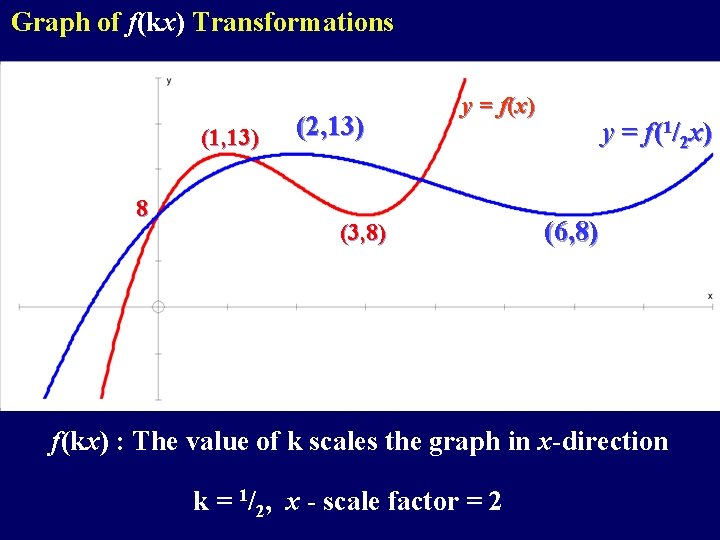
Graph of f(kx) Transformations (1, 13) (2, 13) (1, 13) 88 y =y f= (x)f(x) (3, 8) y = f(1/2 x) (6, 8) f(kx) : The value of k scales the graph in x-direction k = 1/2, x - scale factor = 2

y = logax (a , 1) (a + 2 , 1) (1 , 0) (3 , 0) y = loga(x – 2) Graph moves 2 units to the right

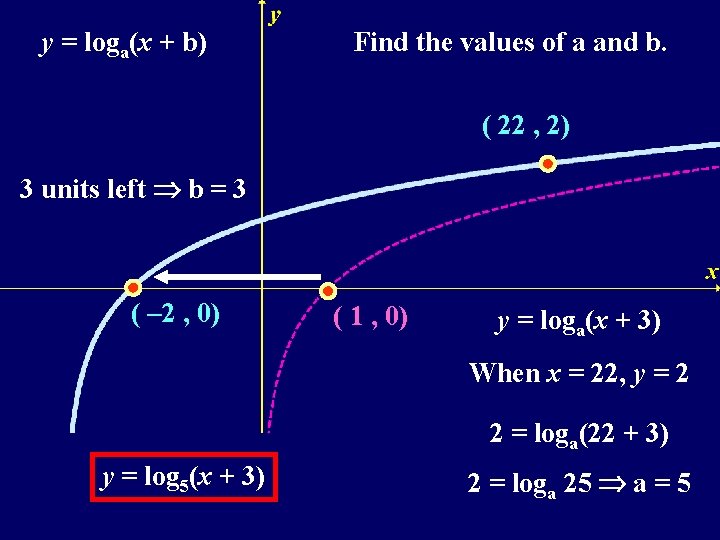
y = loga(x + b) Find the values of a and b. ( 22 , 2) 3 units left b = 3 ( – 2 , 0) ( 1 , 0) y = loga(x + 3) When x = 22, y = 2 2 = loga(22 + 3) y = log 5(x + 3) 2 = loga 25 a = 5

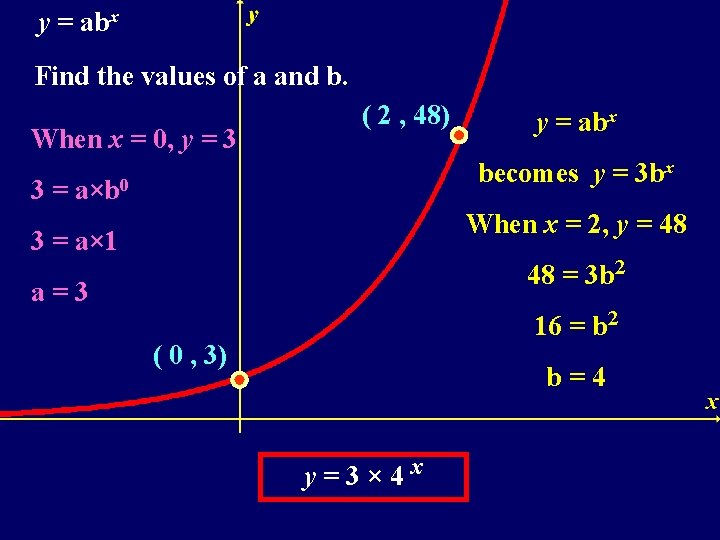
y = abx Find the values of a and b. When x = 0, y = 3 ( 2 , 48) y = abx becomes y = 3 bx 3 = a×b 0 When x = 2, y = 48 3 = a× 1 48 = 3 b 2 a=3 16 = b 2 ( 0 , 3) b=4 y=3× 4 x

The following questions are on Graphs & Functons Non-calculator questions will be indicated

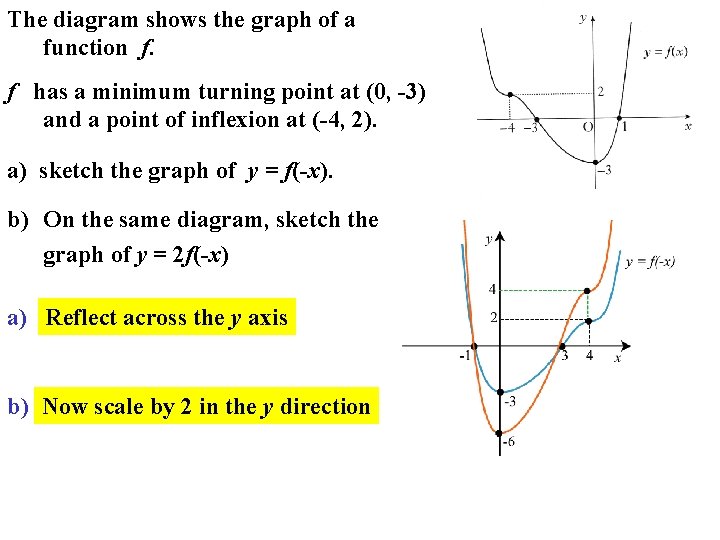
The diagram shows the graph of a function f. f has a minimum turning point at (0, -3) and a point of inflexion at (-4, 2). a) sketch the graph of y = f(-x). b) On the same diagram, sketch the graph of y = 2 f(-x) a) Reflect across the y axis b) Now scale by 2 in the y direction

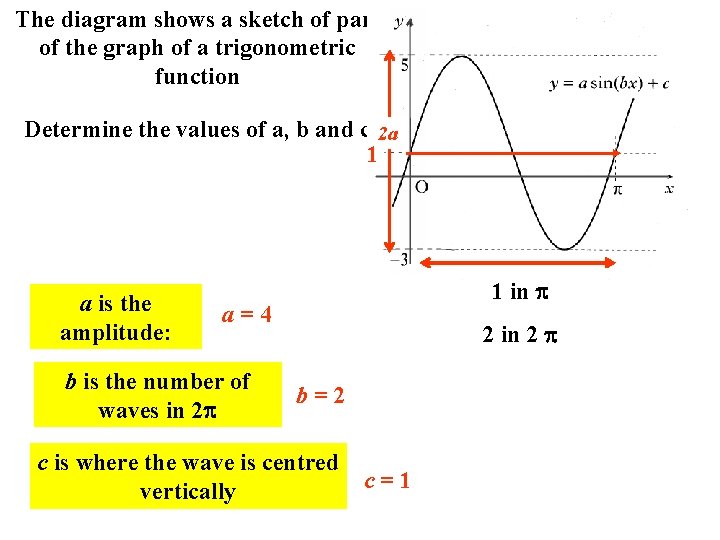
The diagram shows a sketch of part of the graph of a trigonometric function Determine the values of a, b and c 2 a 1 a is the amplitude: 1 in a=4 b is the number of waves in 2 2 in 2 b=2 c is where the wave is centred vertically c=1

a) Express f(x) = x 2 – 4 x + 5 in the form (x – a)2 + b b) On the same diagram sketch (2, 9) i) the graph of y = f(x) ii) the graph of y = 10 - f(x) c) Find the range of values of x for which 10 - f(x) is positive a) c) Solve: 10 - f(x) is positive for -1 < x < 5 b)

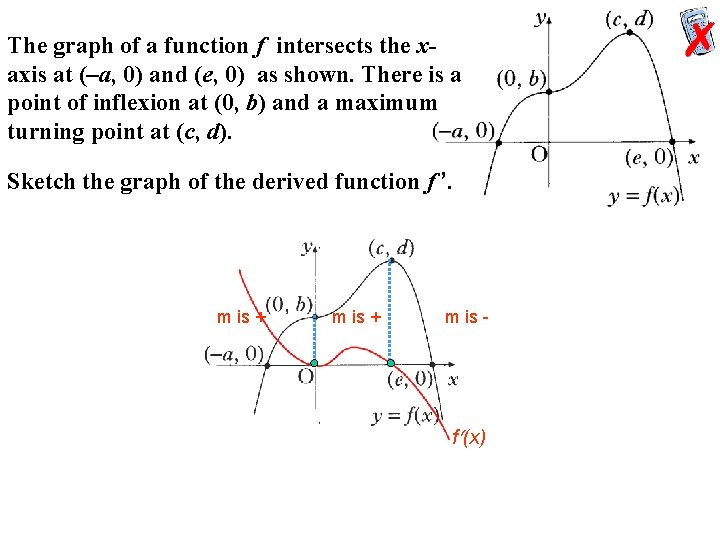
The graph of a function f intersects the xaxis at (–a, 0) and (e, 0) as shown. There is a point of inflexion at (0, b) and a maximum turning point at (c, d). Sketch the graph of the derived function f ’. m is + m is - f (x)

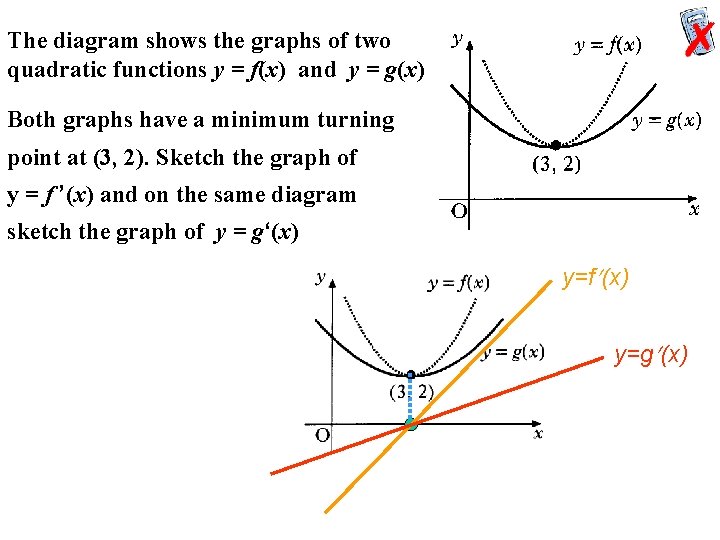
The diagram shows the graphs of two quadratic functions y = f(x) and y = g(x) Both graphs have a minimum turning point at (3, 2). Sketch the graph of y = f ’(x) and on the same diagram sketch the graph of y = g‘(x) y=f (x) y=g (x)

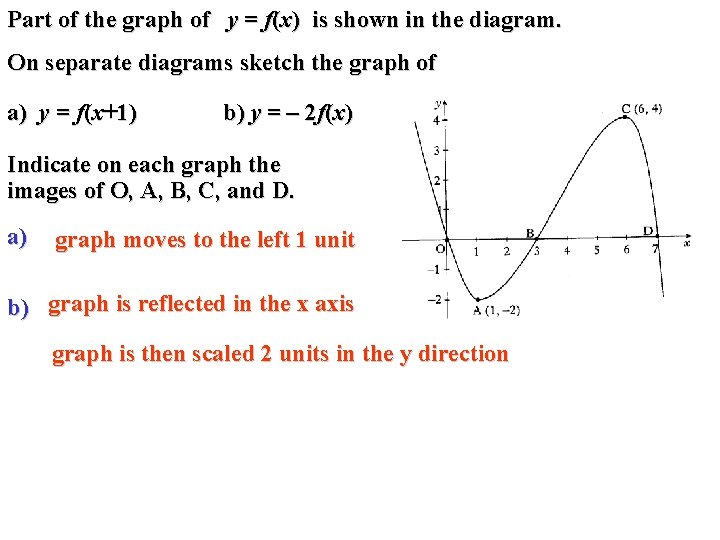
Part of the graph of y = f(x) is shown in the diagram. On separate diagrams sketch the graph of a) y = f(x+1) b) y = – 2 f(x) Indicate on each graph the images of O, A, B, C, and D. a) graph moves to the left 1 unit b) graph is reflected in the x axis graph is then scaled 2 units in the y direction

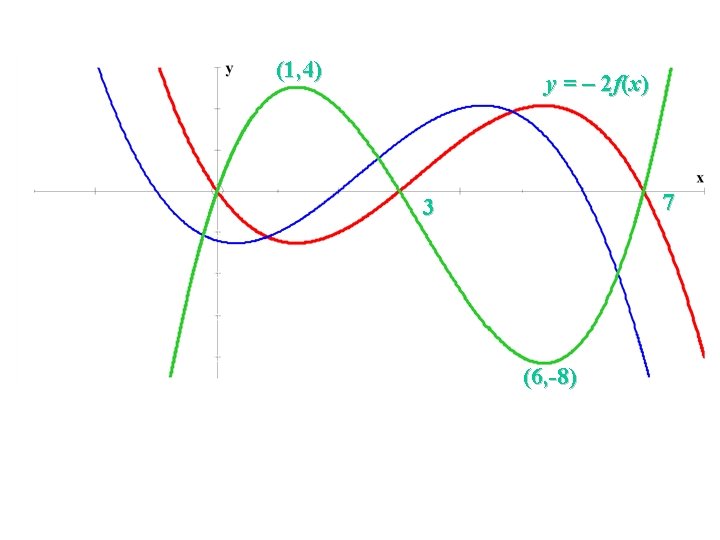
(1, 4) C(5, 4) C(6, 4)y = – 2 f(x) y = f(x+1) 7 3 2 -1 -2 A(-1, 2) 3 7 (6, -8) 7