Pointer analysis Flow insensitive loss of precision S

Pointer analysis

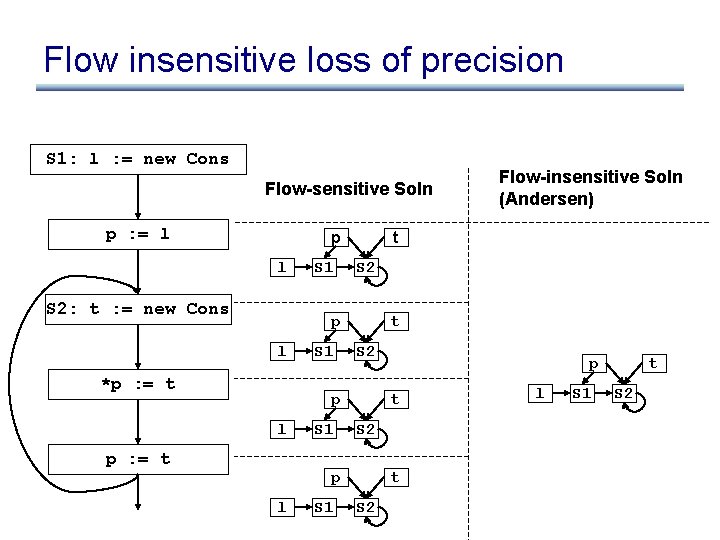
Flow insensitive loss of precision S 1: l : = new Cons Flow-sensitive Soln p : = l p l S 2: t : = new Cons S 1 t S 2 p l *p : = t S 1 t S 2 p l p : = t S 1 p t S 2 p l Flow-insensitive Soln (Andersen) t S 2 l S 1 t S 2

Flow insensitive loss of precision • Flow insensitive analysis leads to loss of precision! main() { x : = &y; . . . Flow insensitive analysis tells us that x may point to z here! x : = &z; } • However: – uses less memory (memory can be a big bottleneck to running on large programs) – runs faster

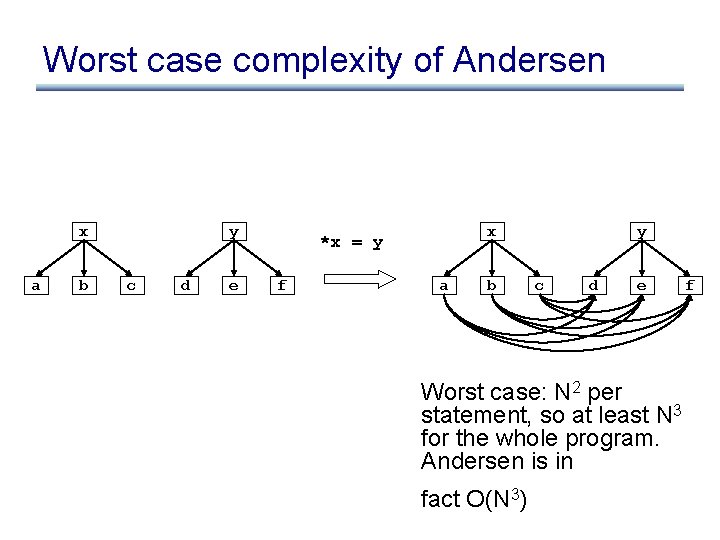
Worst case complexity of Andersen x a b y c d e x *x = y f a b y c d e Worst case: N 2 per statement, so at least N 3 for the whole program. Andersen is in fact O(N 3) f

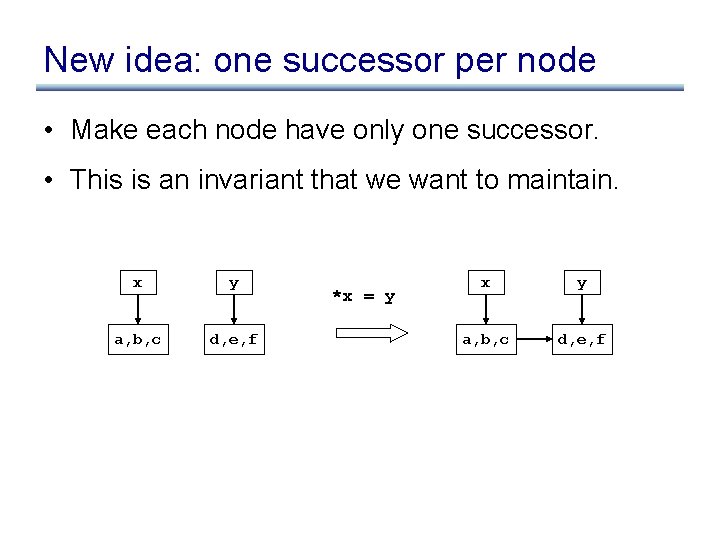
New idea: one successor per node • Make each node have only one successor. • This is an invariant that we want to maintain. x y a, b, c d, e, f *x = y x y a, b, c d, e, f

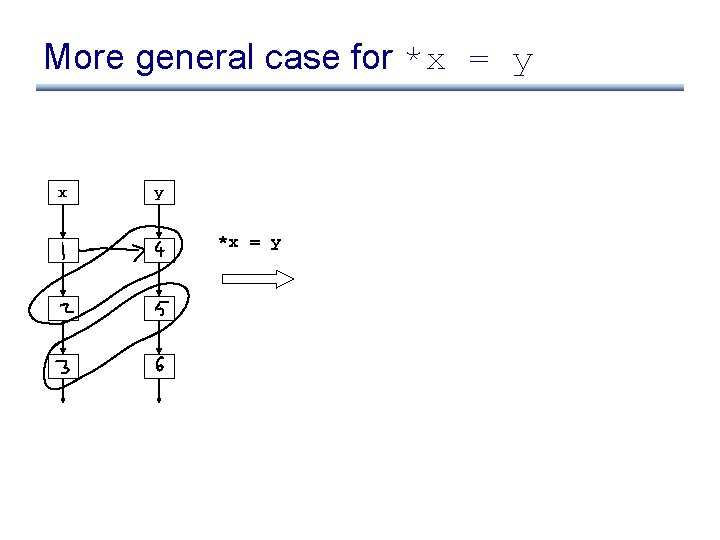
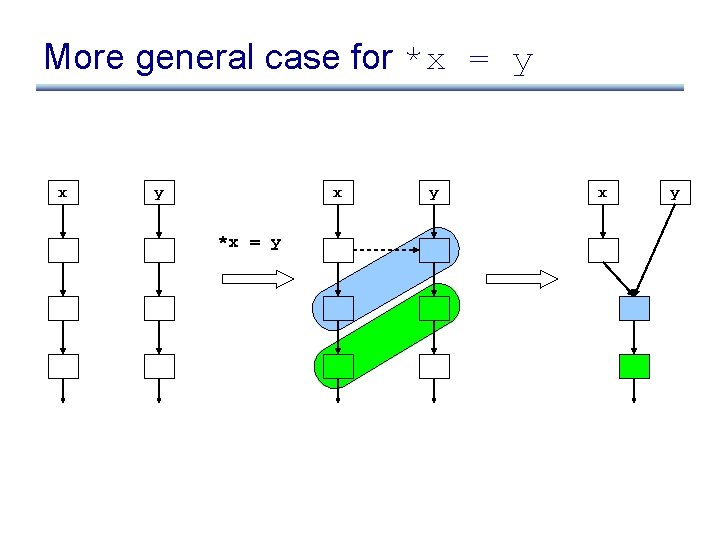
More general case for *x = y x y *x = y

More general case for *x = y x *x = y y x y

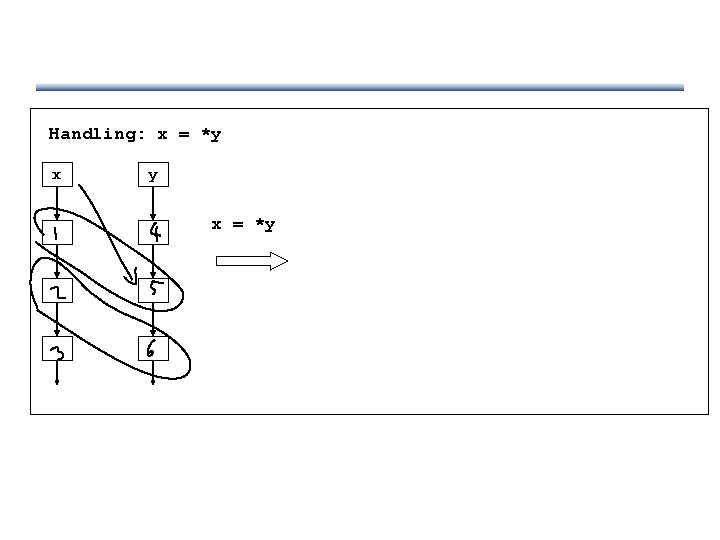
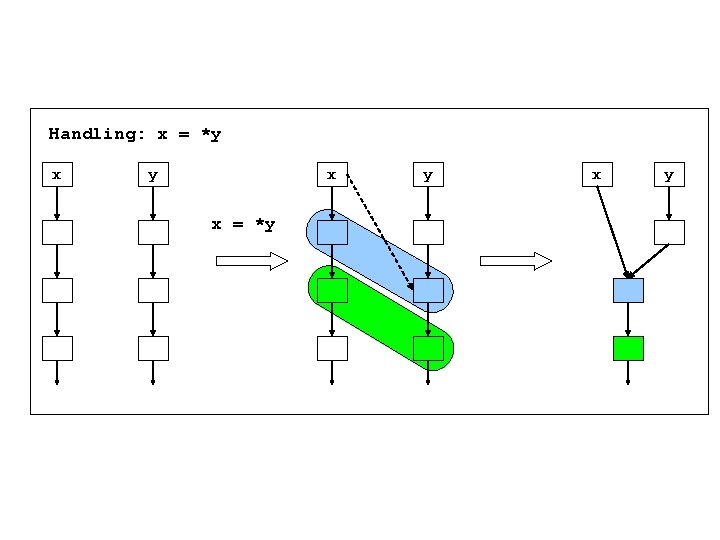
Handling: x = *y

Handling: x = *y x x = *y y x y

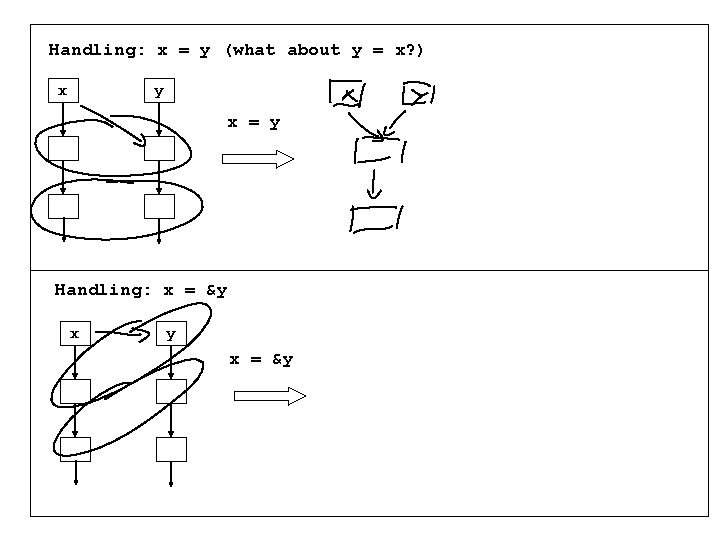
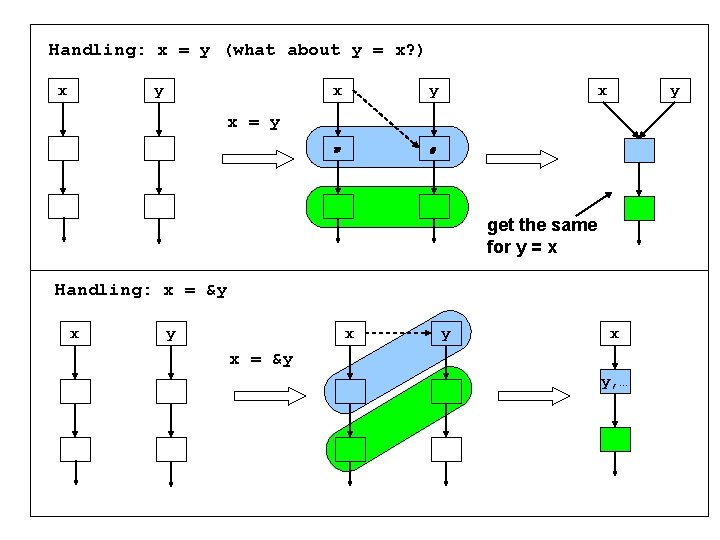
Handling: x = y (what about y = x? ) x y x = y Handling: x = &y

Handling: x = y (what about y = x? ) x y x y x = y get the same for y = x Handling: x = &y x y x x = &y y, …

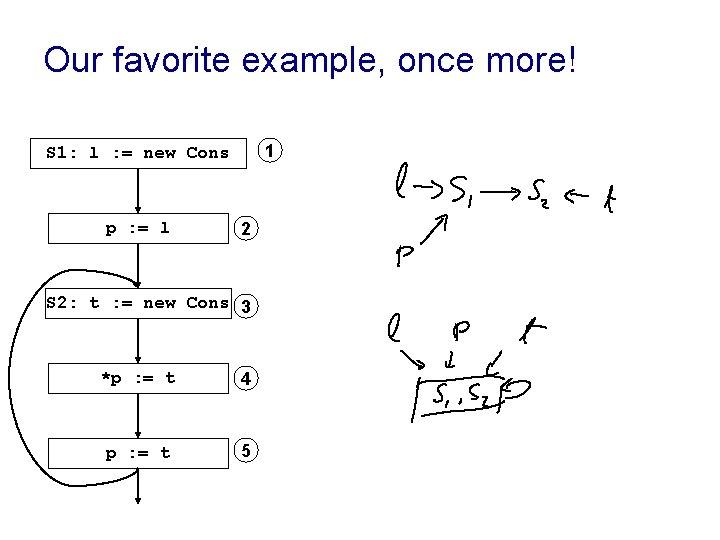
Our favorite example, once more! 1 S 1: l : = new Cons p : = l 2 S 2: t : = new Cons 3 *p : = t 4 p : = t 5

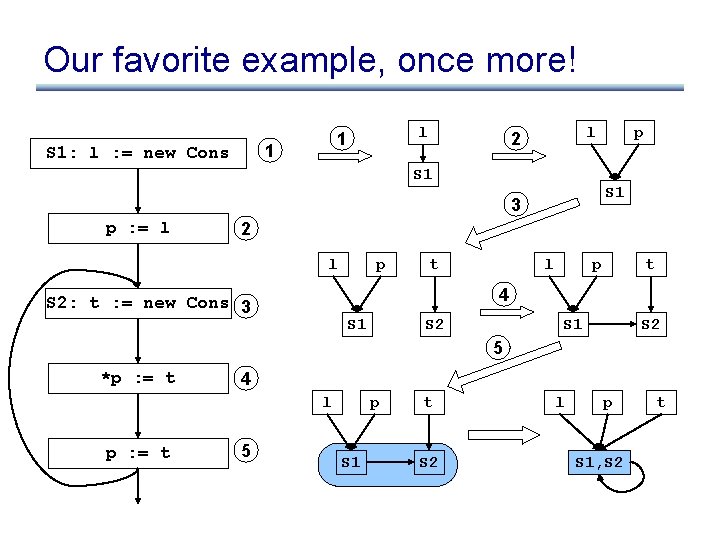
Our favorite example, once more! 1 S 1: l : = new Cons l 1 l 2 S 1 3 p : = l p 2 l p t 4 S 2: t : = new Cons 3 S 1 S 2 5 *p : = t 4 l p : = t 5 p S 1 t S 2 l p S 1, S 2 t

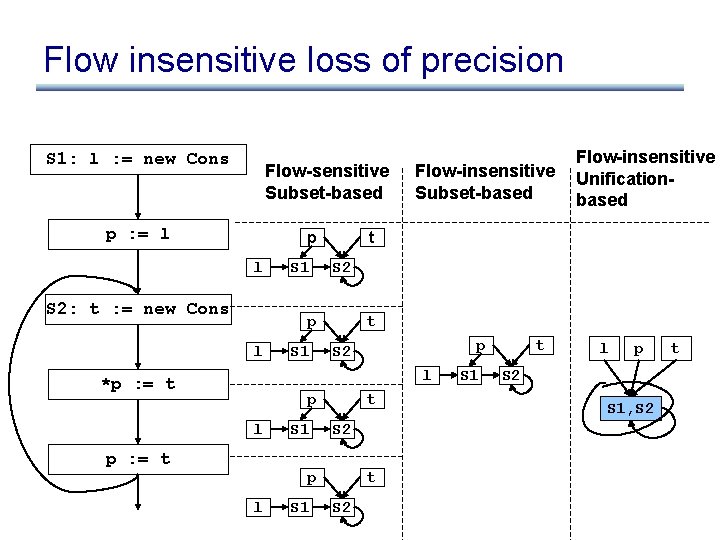
Flow insensitive loss of precision S 1: l : = new Cons Flow-sensitive Subset-based p : = l p l S 2: t : = new Cons S 1 t S 2 p l S 1 Flow-insensitive Subset-based t p S 2 l *p : = t p l p : = t S 1 t S 2 p l S 1 Flow-insensitive Unificationbased t S 2 S 1 t l p S 2 S 1, S 2 t

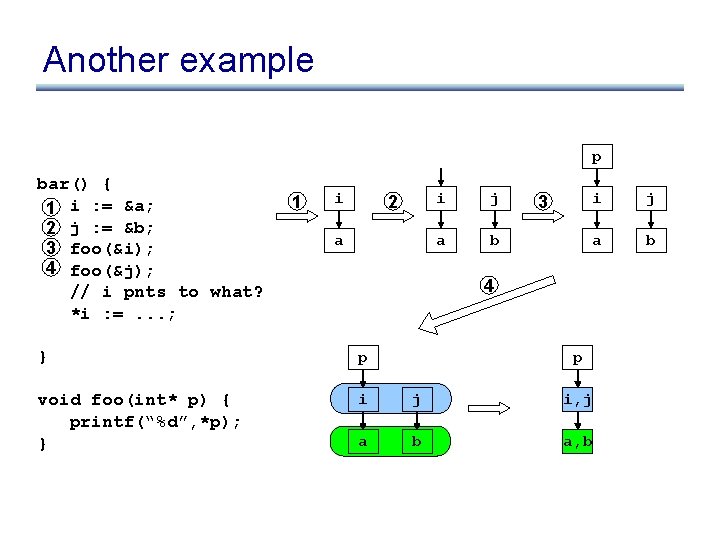
Another example bar() { 1 i : = &a; 2 j : = &b; 3 foo(&i); 4 foo(&j); // i pnts to what? *i : =. . . ; } void foo(int* p) { printf(“%d”, *p); }

Another example p bar() { 1 i : = &a; 2 j : = &b; 3 foo(&i); 4 foo(&j); // i pnts to what? *i : =. . . ; 1 i 2 a i j a b 3 i j a b 4 } p void foo(int* p) { printf(“%d”, *p); } i j i, j a b a, b p

Steensgaard & beyond • A well engineered implementation of Steensgaard ran on Word 97 (2. 1 MLOC) in 1 minute. • One Level Flow (Das PLDI 00) is an extension to Steensgaard that gets more precision and runs in 2 minutes on Word 97.

Correctness

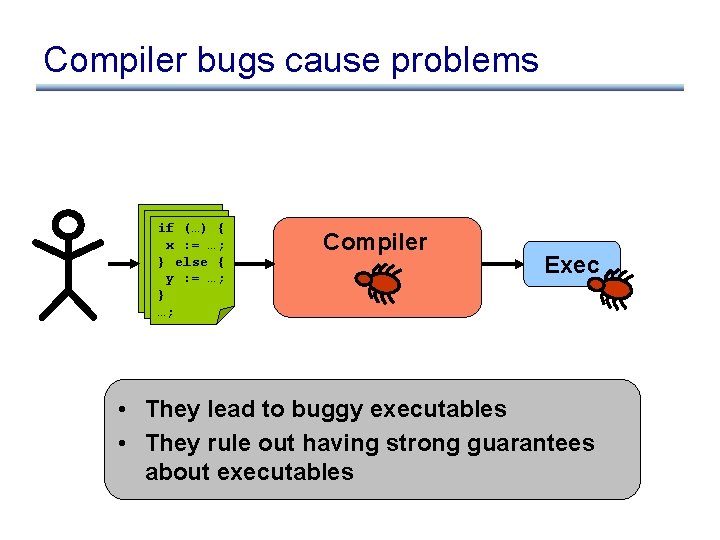
Compilers have many bugs Searched for “incorrect” and “wrong” in the gccbugs mailing list. Some of the results: • • • [Bug middle-end/19650] New: miscompilation of correct code [Bug c++/19731] arguments incorrectly named in static member specialization [Bug rtl-optimization/13300] Variable incorrectly identified as a biv [Bug rtl-optimization/16052] strength reduction produces wrong code [Bug tree-optimization/19633] local address incorrectly thought to escape [Bug target/19683] New: MIPS wrong-code for 64 -bit multiply [Bug c++/19605] Wrong member offset in inherited classes Bug java/19295] [4. 0 regression] Incorrect bytecode produced for bitwise AND … Total of 545 matches… And this is only for one month! On a mature compiler!

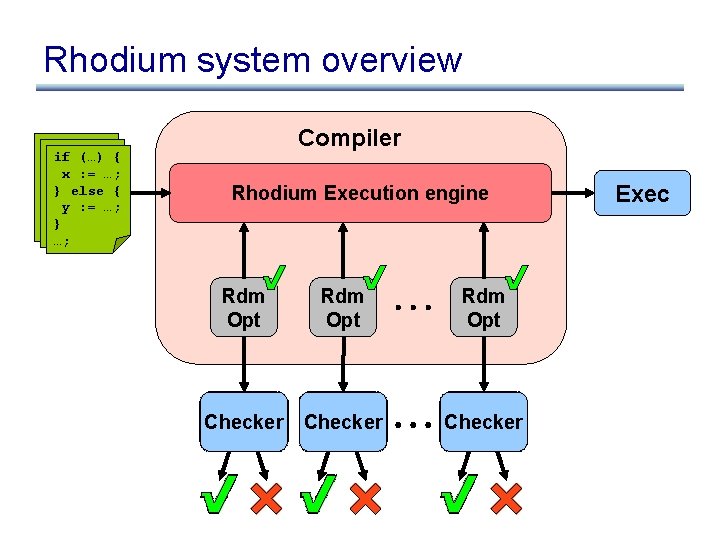
Compiler bugs cause problems if (…) { x : = …; } else { y : = …; } …; Compiler Exec • They lead to buggy executables • They rule out having strong guarantees about executables

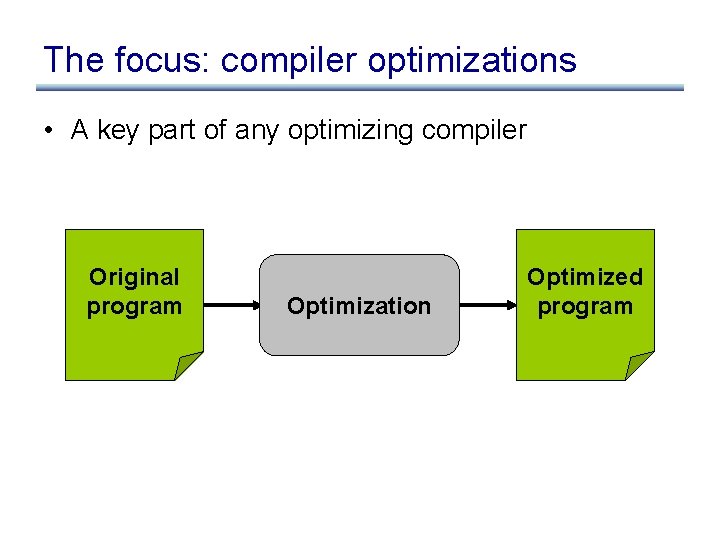
The focus: compiler optimizations • A key part of any optimizing compiler Original program Optimization Optimized program

The focus: compiler optimizations • A key part of any optimizing compiler • Hard to get optimizations right – Lots of infrastructure-dependent details – There are many corner cases in each optimization – There are many optimizations and they interact in unexpected ways – It is hard to test all these corner cases and all these interactions

Goals • Make it easier to write compiler optimizations – student in an undergrad compiler course should be able to write optimizations • Provide strong guarantees about the correctness of optimizations – automatically (no user intervention at all) – statically (before the opts are even run once) • Expressive enough for realistic optimizations

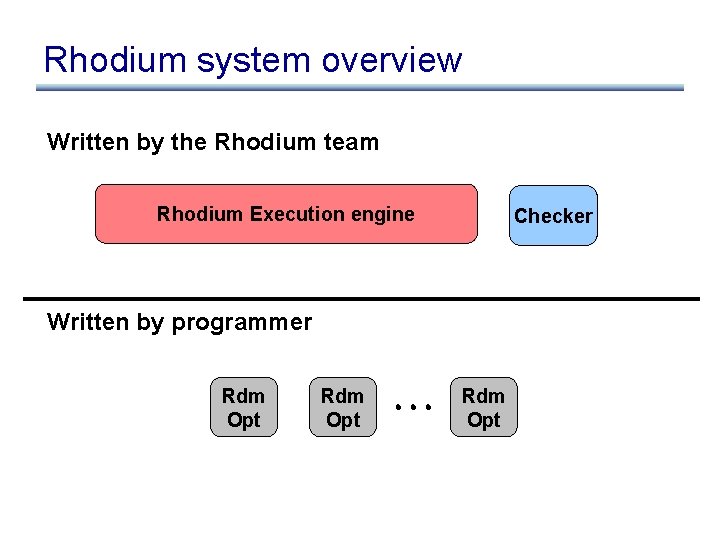
The Rhodium work • A domain-specific language for writing optimizations: Rhodium • A correctness checker for Rhodium optimizations • An execution engine for Rhodium optimizations • Implemented and checked the correctness of a variety of realistic optimizations

Broader implications • Many other kinds of program manipulators: code refactoring tools, static checkers – Rhodium work is about program analyses and transformations, the core of any program manipulator • Enables safe extensible program manipulators – Allow end programmers to easily and safely extend program manipulators – Improve programmer productivity

Outline • Introduction • Overview of the Rhodium system • Writing Rhodium optimizations • Checking Rhodium optimizations • Discussion

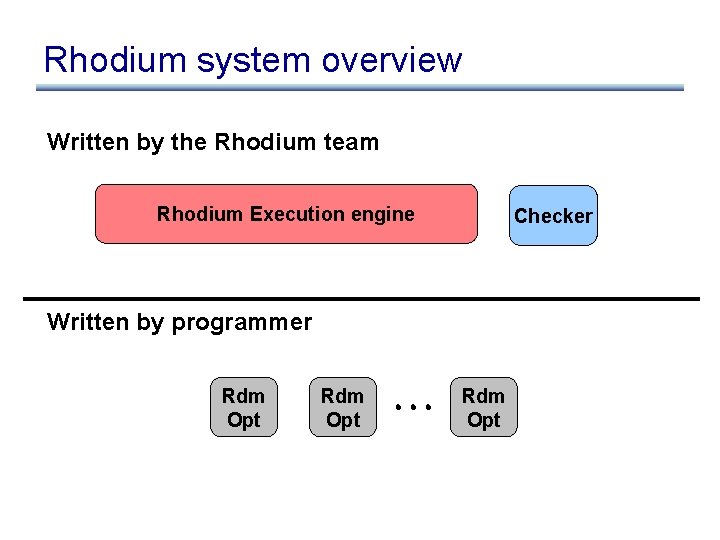
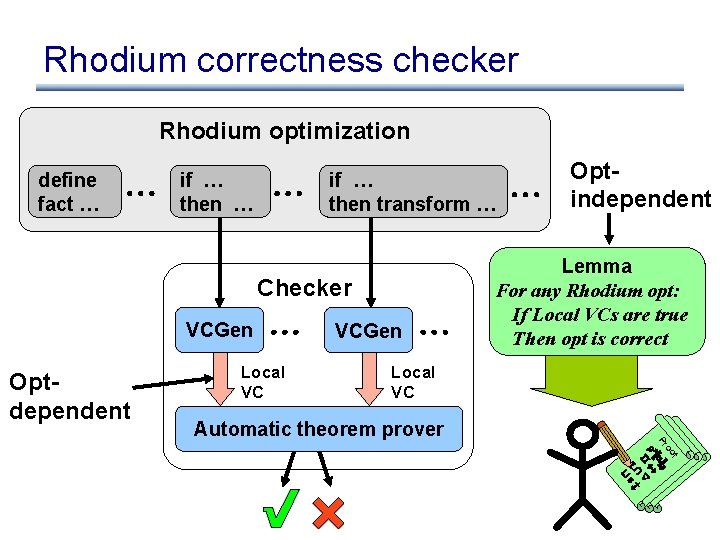
Rhodium system overview Written by the Rhodium team Rhodium Execution engine Checker Written by programmer Rdm Opt

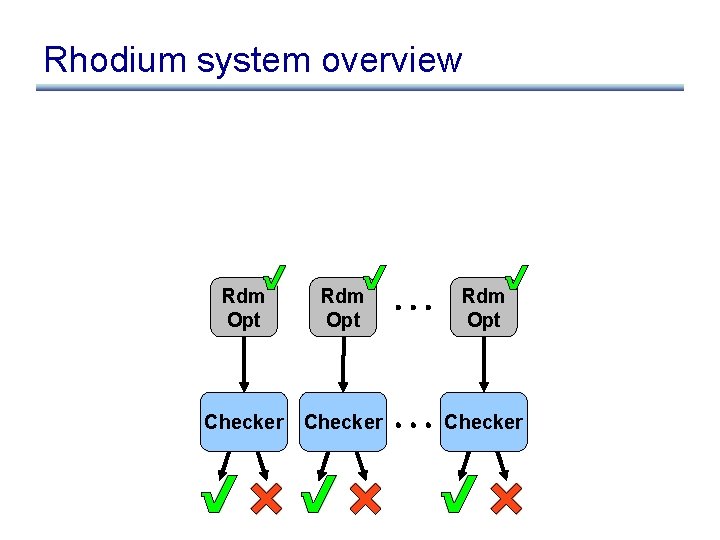
Rhodium system overview Written by the Rhodium team Rhodium Execution engine Checker Written by programmer Rdm Opt

Rhodium system overview Rdm Opt Checker

Rhodium system overview if (…) { x : = …; } else { y : = …; } …; Compiler Rhodium Execution engine Rdm Opt Checker Exec

The technical problem • Tension between: – Expressiveness – Automated correctness checking • Challenge: develop techniques – that will go a long way in terms of expressiveness – that allow correctness to be checked

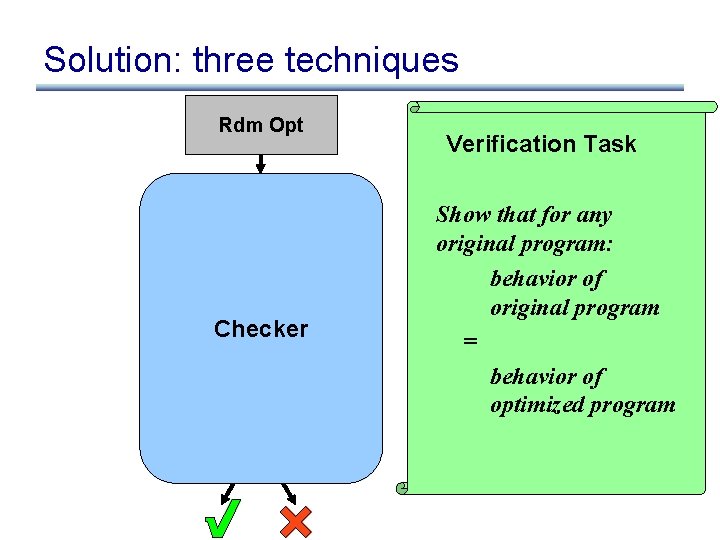
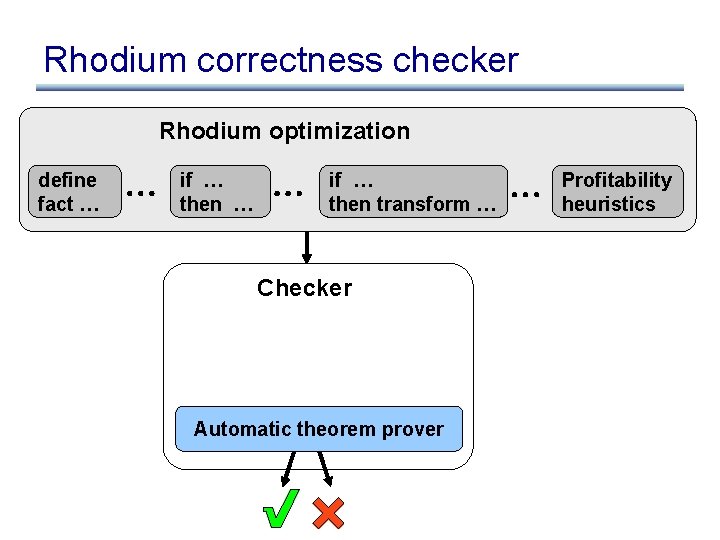
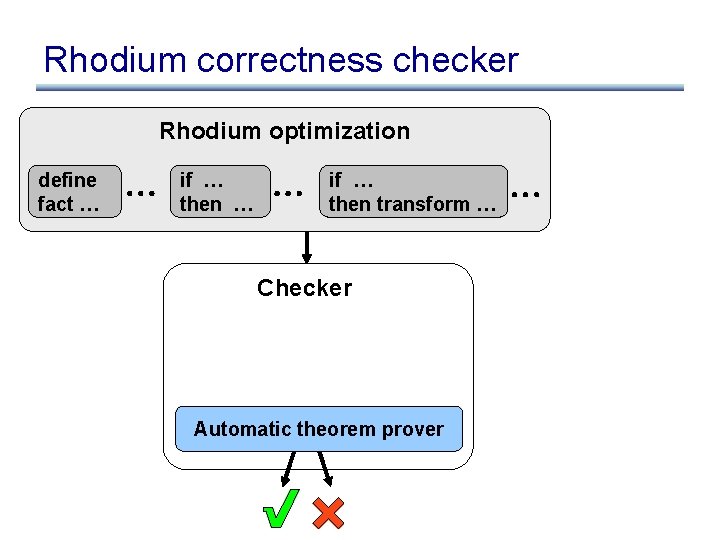
Solution: three techniques Rdm Opt Verification Task Checker Automatic Theorem Prover Verification Task Show that for any original program: behavior of original program = behavior of optimized program

Solution: three techniques Rdm Opt Verification Task Automatic Theorem Prover Verification Task

Solution: three techniques Rdm Opt Verification Task Automatic Theorem Prover Verification Task

Solution: three techniques Rdm Opt 1. Rhodium is declarative – declare intent using rules – execution engine takes care of the rest Automatic Theorem Prover

Solution: three techniques Rdm Opt 1. Rhodium is declarative – declare intent using rules – execution engine takes care of the rest Automatic Theorem Prover

Solution: three techniques Part that must be reasoned about Rdm Opt Heuristics not affecting correctness 1. Rhodium is declarative 2. Factor out heuristics – legal transformations – vs. profitable transformations Automatic Theorem Prover

Solution: three techniques Heuristics not affecting correctness Part that must be reasoned about 1. Rhodium is declarative 2. Factor out heuristics – legal transformations – vs. profitable transformations Automatic Theorem Prover

Solution: three techniques optdependent 1. Rhodium is declarative optindependent 2. Factor out heuristics Automatic Theorem Prover 3. Split verification task – opt-dependent – vs. opt-independent

Solution: three techniques 1. Rhodium is declarative 2. Factor out heuristics Automatic Theorem Prover 3. Split verification task – opt-dependent – vs. opt-independent

Solution: three techniques 1. Rhodium is declarative 2. Factor out heuristics Automatic Theorem Prover 3. Split verification task – opt-dependent – vs. opt-independent

Solution: three techniques 1. Rhodium is declarative 2. Factor out heuristics 3. Split verification task Automatic Theorem Prover Result: • Expressive language • Automated correctness checking

Outline • Introduction • Overview of the Rhodium system • Writing Rhodium optimizations • Checking Rhodium optimizations • Discussion

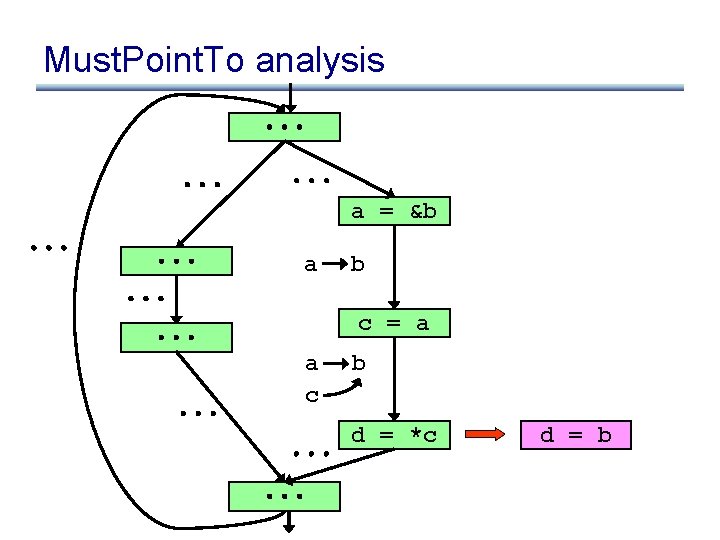
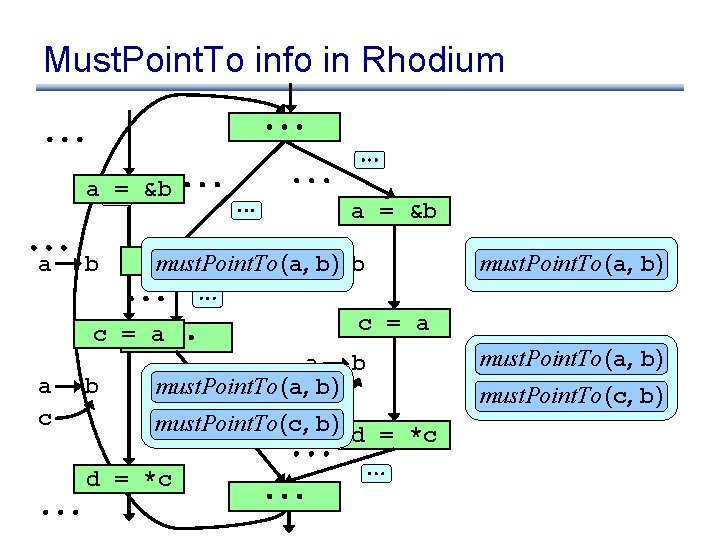
Must. Point. To analysis a = &b a b c = a a c b d = *c d = b

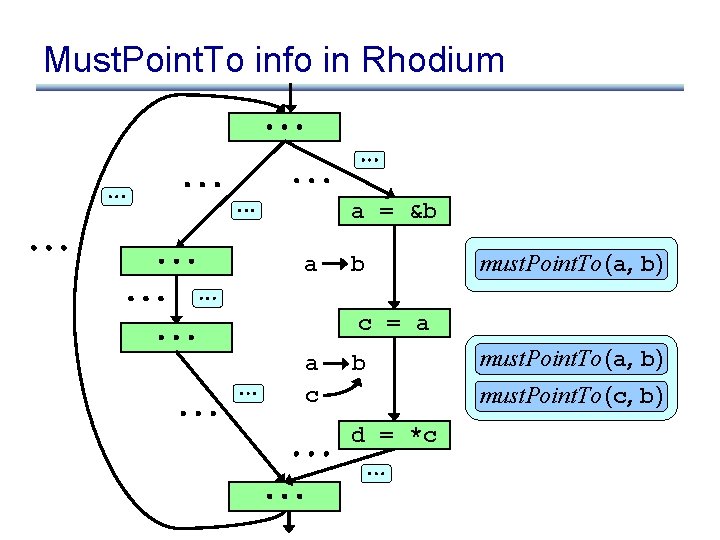
Must. Point. To info in Rhodium a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c

Must. Point. To info in Rhodium a = &b a b must. Point. To (a, ab) b c = a a c b a = &b c = a a b must. Point. To (a, cb) must. Point. To (c, b) d = *c must. Point. To (a, b) must. Point. To (c, b)

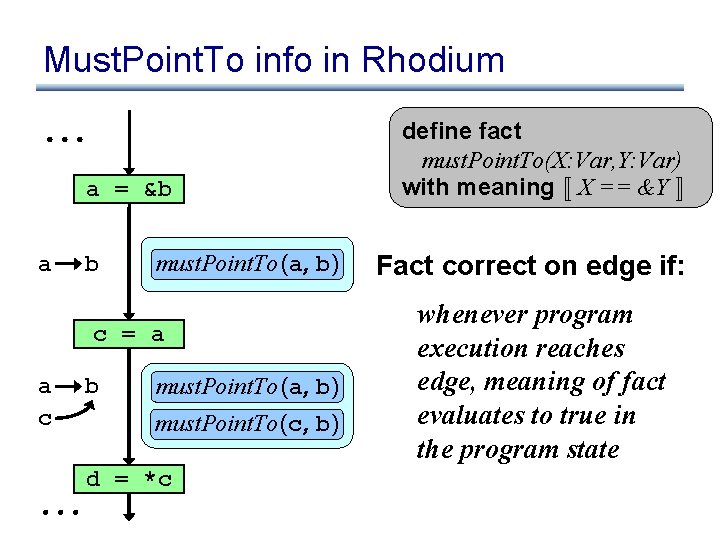
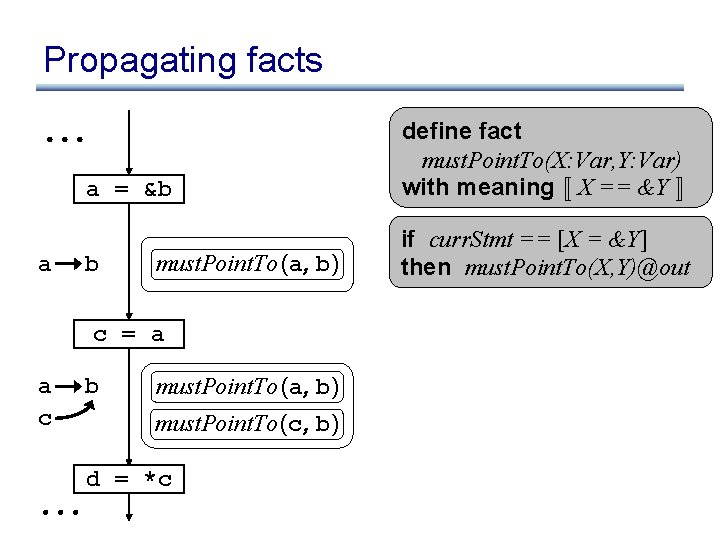
Must. Point. To info in Rhodium a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ Fact correct on edge if: whenever program execution reaches edge, meaning of fact evaluates to true in the program state

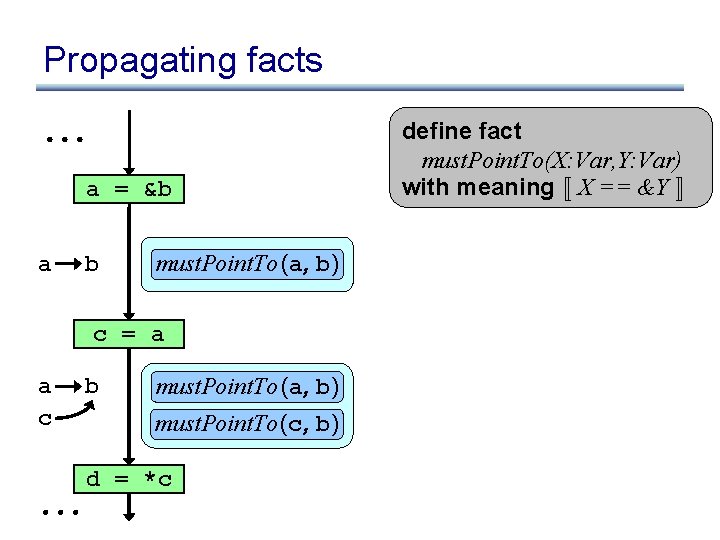
Propagating facts a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬

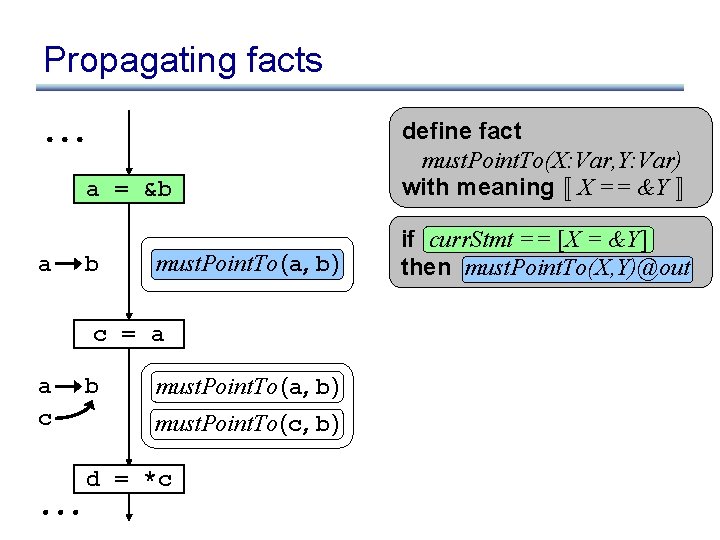
Propagating facts a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ if curr. Stmt == [X = &Y] then must. Point. To(X, Y)@out

Propagating facts a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ if curr. Stmt == [X = &Y] then must. Point. To(X, Y)@out

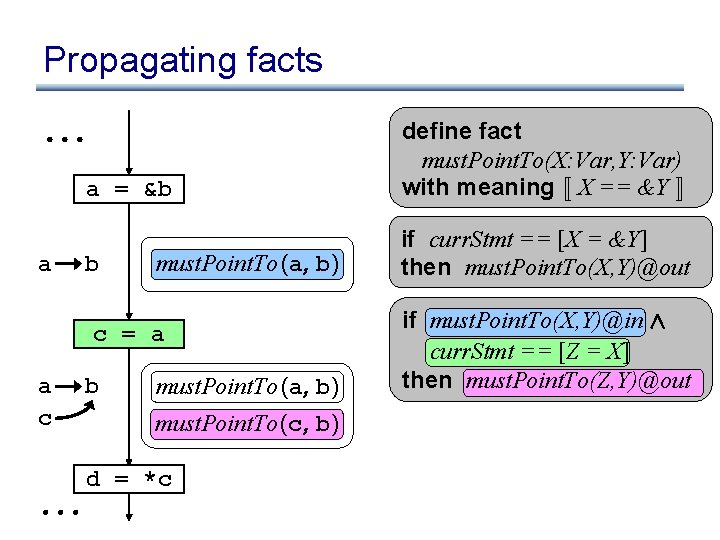
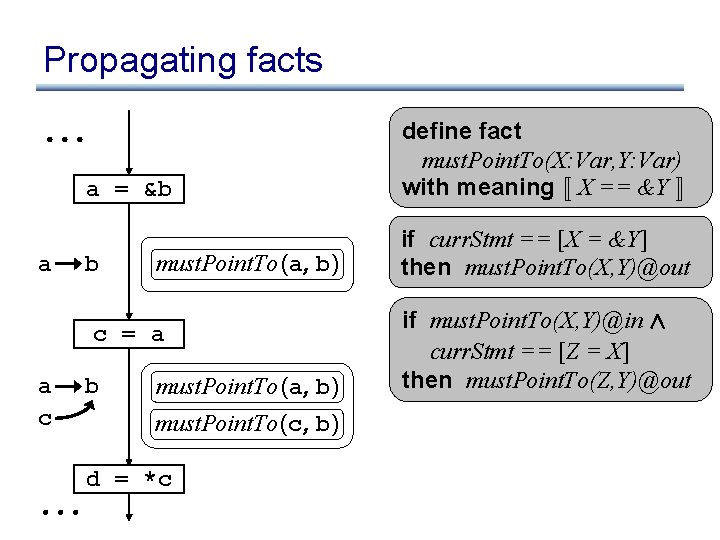
Propagating facts a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ if curr. Stmt == [X = &Y] then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = X] then must. Point. To(Z, Y)@out

Propagating facts a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ if curr. Stmt == [X = &Y] then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = X] then must. Point. To(Z, Y)@out

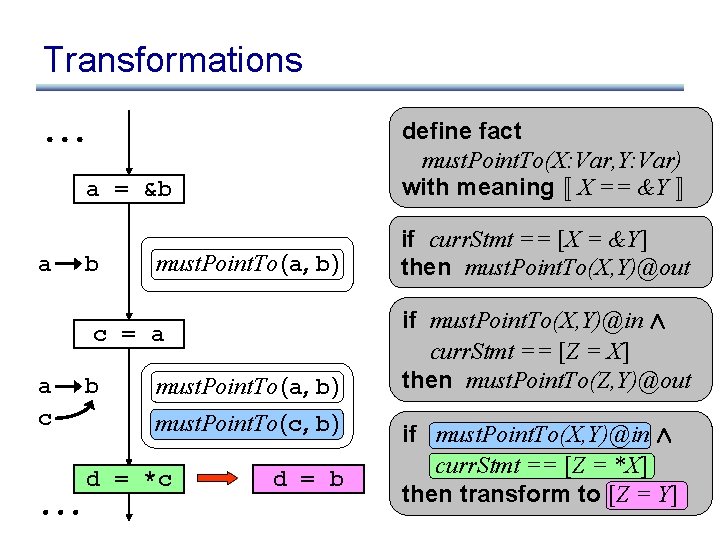
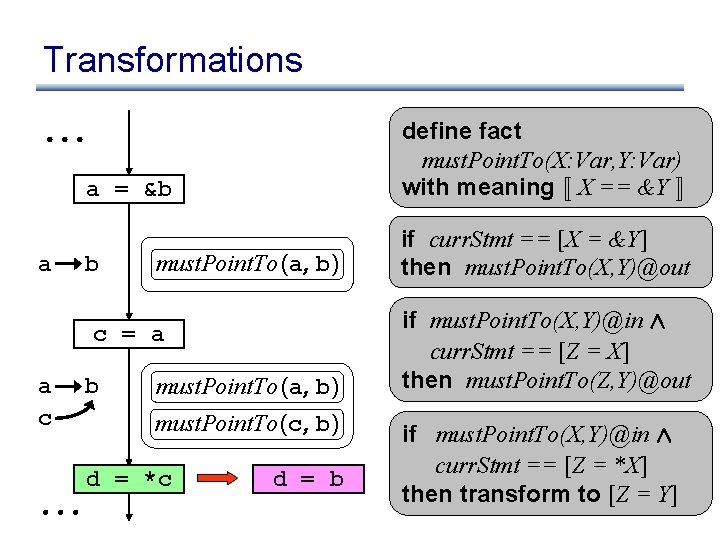
Transformations define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c d = b if curr. Stmt == [X = &Y] then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = X] then must. Point. To(Z, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = *X] then transform to [Z = Y]

Transformations define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ a = &b a b must. Point. To (a, b) c = a a c b must. Point. To (a, b) must. Point. To (c, b) d = *c d = b if curr. Stmt == [X = &Y] then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = X] then must. Point. To(Z, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = *X] then transform to [Z = Y]

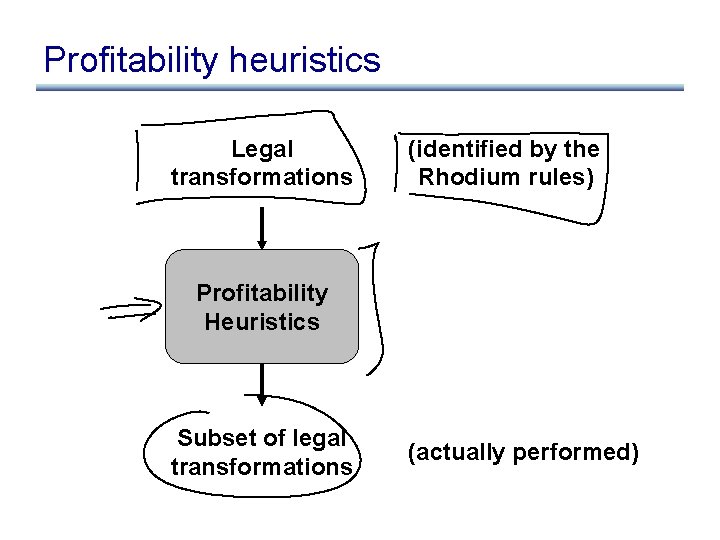
Profitability heuristics Legal transformations (identified by the Rhodium rules) Profitability Heuristics Subset of legal transformations (actually performed)

Profitability heuristic example 1 • Inlining • Many heuristics to determine when to inline a function – compute function sizes, estimate code-size increase, estimate performance benefit – maybe even use AI techniques to make the decision • However, these heuristics do not affect the correctness of inlining • They are just used to choose which of the correct set of transformations to perform

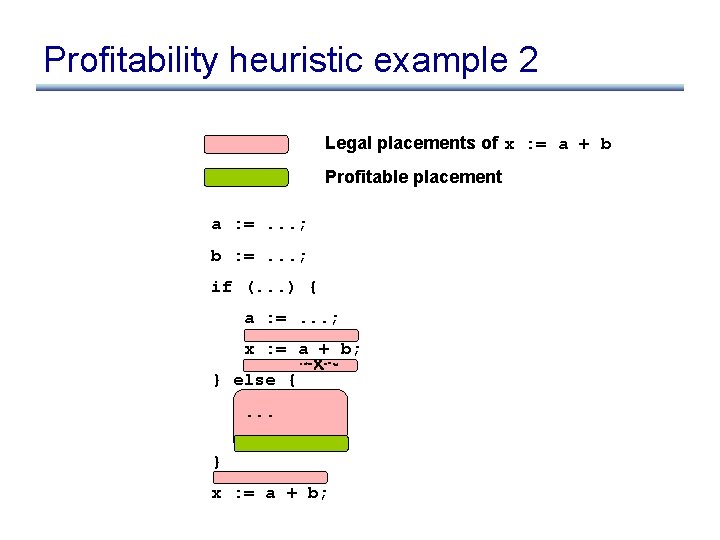
Profitability heuristic example 2 • Partial redundancy elimination (PRE) a : =. . . ; b : =. . . ; if (. . . ) { a : =. . . ; x : = a + b; } else {. . . } x : = a + b;

Profitability heuristic example 2 • PRE as code duplication followed by CSE a : =. . . ; b : =. . . ; if (. . . ) { a : =. . . ; x : = a + b; } else {. . . } x : = a + b; • Code duplication

Profitability heuristic example 2 • PRE as code duplication followed by CSE a : =. . . ; b : =. . . ; if (. . . ) { a : =. . . ; x : = a + b; } else {. . . x : = a + b; } x : = a x; + b; • Code duplication • CSE

Profitability heuristic example 2 • PRE as code duplication followed by CSE a : =. . . ; b : =. . . ; if (. . . ) { a : =. . . ; x : = a + b; } else {. . . x : = a + b; } x : = x; • Code duplication • CSE • self-assignment removal

Profitability heuristic example 2 Legal placements of x : = a + b Profitable placement a : =. . . ; b : =. . . ; if (. . . ) { a : =. . . ; x : = a + b; } else {. . . } x : = a + b;

Semantics of a Rhodium opt • Run propagation rules in a loop until there are no more changes (optimistic iterative analysis) • Then run transformation rules to identify the set of legal transformations • Then run profitability heuristics to determine set of transformations to perform

More facts define fact must. Not. Point. To(X: Var, Y: Var) with meaning « X &Y ¬ define fact does. Not. Point. Into. Heap(X: Var) with meaning « X == null Ç 9 Y: Var. X == &Y ¬ define fact has. Constant. Value(X: Var, C: Const) with meaning « X == C ¬

More rules if curr. Stmt == [X = *A] Æ must. Not. Point. To. Heap(A)@in Æ 8 B: Var. may. Point. To(A, B)@in ) must. Not. Point. To(B, Y) then must. Not. Point. To(X, Y)@out if curr. Stmt == [Y = I + BE ] Æ var. Equal. Array(X, A, J)@in Æ equals. Plus(J, I, BE)@in Æ : may. Def(X) Æ : may. Def. Array(A) Æ unchanged(BE) then var. Equal. Array(X, A, Y)@out

More in Rhodium • More powerful pointer analyses – Heap summaries • Analyses across procedures – Interprocedural analyses • Analyses that don’t care about the order of statements – Flow-insensitive analyses

Outline • Introduction • Overview of the Rhodium system • Writing Rhodium optimizations • Checking Rhodium optimizations • Discussion

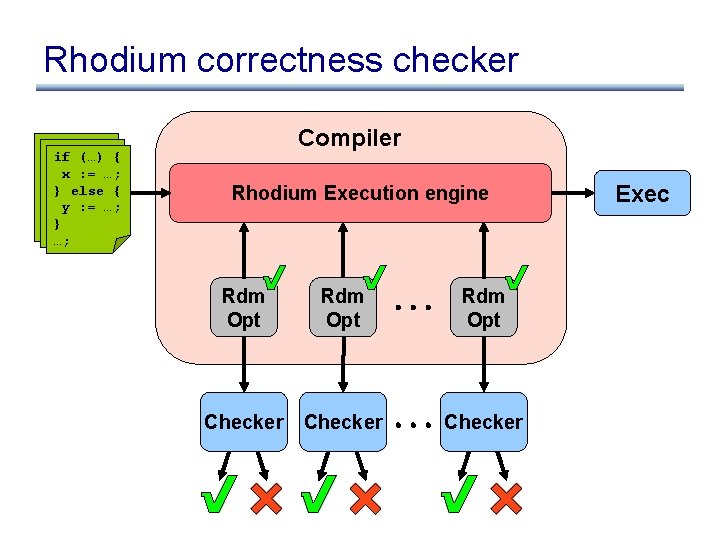
Rhodium correctness checker if (…) { x : = …; } else { y : = …; } …; Compiler Rhodium Execution engine Rdm Opt Checker Exec

Rhodium correctness checker Checker Rdm Opt Checker

Rhodium correctness checker Rdm Opt Checker Automatic theorem prover

Rhodium correctness checker Rhodium optimization define fact … if … then transform … Checker Automatic theorem prover Profitability heuristics

Rhodium correctness checker Rhodium optimization define fact … if … then transform … Checker Automatic theorem prover

Rhodium correctness checker Rhodium optimization define fact … if … then transform … Checker VCGen Optdependent Local VC VCGen Optindependent Lemma For any Rhodium opt: If Local VCs are true Then opt is correct Local VC f oo ¬ Pr « $ r l t Automatic theorem prover

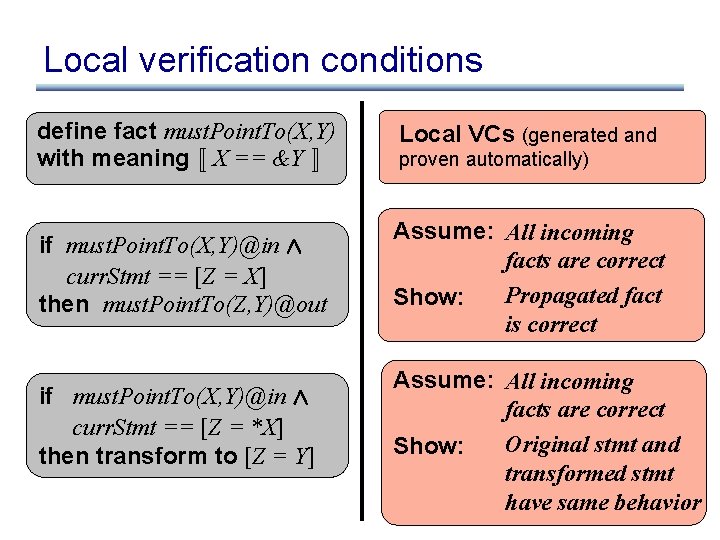
Local verification conditions define fact must. Point. To(X, Y) with meaning « X == &Y ¬ if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = X] then must. Point. To(Z, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = *X] then transform to [Z = Y] Local VCs (generated and proven automatically) Assume: All incoming facts are correct Propagated fact Show: is correct Assume: All incoming facts are correct Original stmt and Show: transformed stmt have same behavior

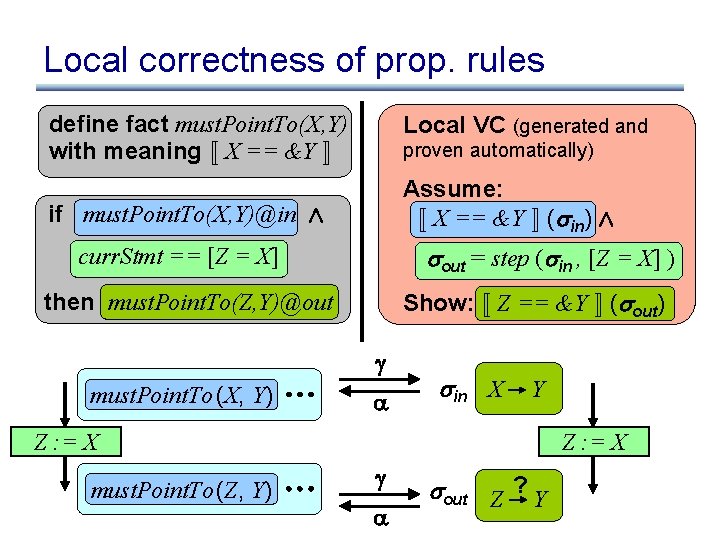
Local correctness of prop. rules define fact must. Point. To(X, Y) with meaning « X == &Y ¬ if must. Point. To(X, Y)@in Æ curr. Stmt == [Z = X] then must. Point. To(Z, Y)@out must. Point. To (X, Y) Z : = X must. Point. To (Z, Y) Local VC (generated and proven automatically) Assume: All incoming « X == &Y ¬ ( are facts correct in) Æ out = step ( in , [Z =fact X] ) Propagated Show: correct Show: « Zis== &Y ¬ ( ) out

Local correctness of prop. rules define fact must. Point. To(X, Y) with meaning « X == &Y ¬ Local VC (generated and proven automatically) Assume: « X == &Y ¬ ( in) Æ if must. Point. To(X, Y)@in Æ out = step ( in , [Z = X] ) curr. Stmt == [Z = X] Show: « Z == &Y ¬ ( out) then must. Point. To(Z, Y)@out must. Point. To (X, Y) in X Y Z : = X must. Point. To (Z, Y) Z : = X out Z ? Y

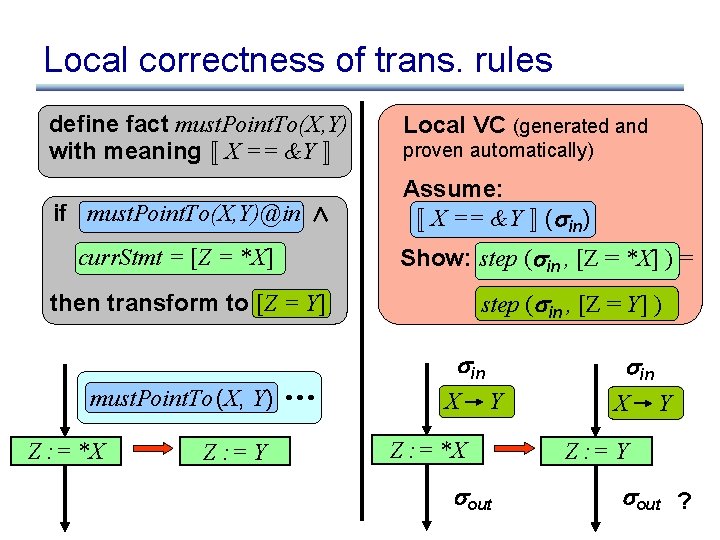
Local correctness of trans. rules define fact must. Point. To(X, Y) with meaning « X == &Y ¬ if must. Point. To(X, Y)@in Æ curr. Stmt = [Z = *X] then transform to [Z = Y] must. Point. To (X, Y) Z : = *X Z : = Y Local VC (generated and proven automatically) Assume: All incoming facts « X == &Y ¬ (are in)correct Original stmt and Show: step ( in , [Z = *X] ) = transformed stmt have step ( insame , [Z behavior = Y] )

Local correctness of trans. rules define fact must. Point. To(X, Y) with meaning « X == &Y ¬ if must. Point. To(X, Y)@in Æ curr. Stmt = [Z = *X] Local VC (generated and proven automatically) Assume: « X == &Y ¬ ( in) Show: step ( in , [Z = *X] ) = step ( in , [Z = Y] ) then transform to [Z = Y] in must. Point. To (X, Y) Z : = *X Z : = Y X in Y Z : = *X out X Y Z : = Y out ?

Outline • Introduction • Overview of the Rhodium system • Writing Rhodium optimizations • Checking Rhodium optimizations • Discussion

Topics of Discussion • Correctness guarantees • Usefulness of the checker • Expressiveness

• Guarantees Correctness guarantees • Usefulness • Expressiveness • Once checked, optimizations are guaranteed to be correct • Caveat: trusted computing base – execution engine – checker implementation – proofs done by hand once • Adding a new optimization does not increase the size of the trusted computing base

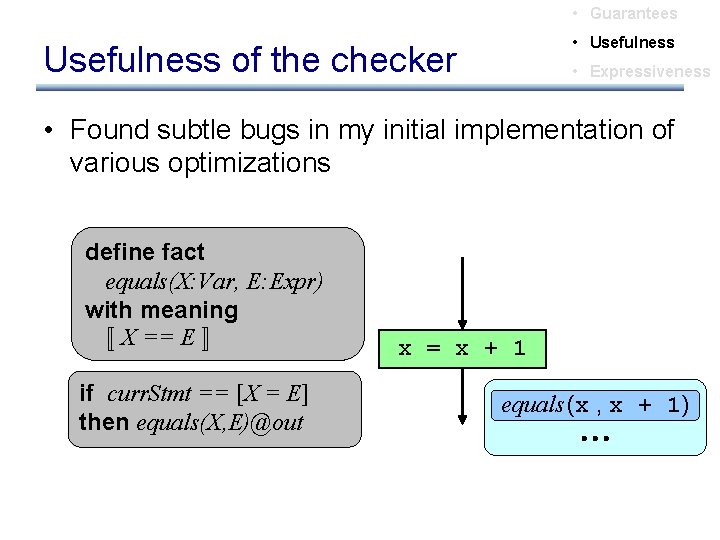
• Guarantees • Usefulness of the checker • Expressiveness • Found subtle bugs in my initial implementation of various optimizations define fact equals(X: Var, E: Expr) with meaning « X == E ¬ if curr. Stmt == [X = E] then equals(X, E)@out xx : = = xx ++ 11 equals (x , x + 1)

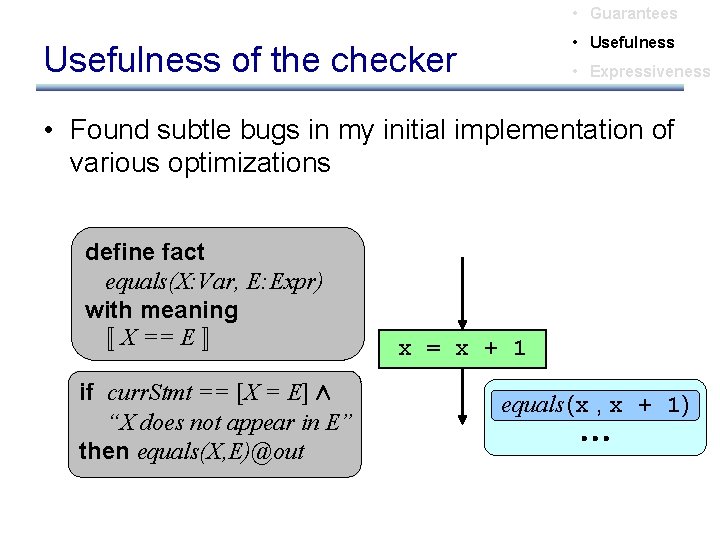
• Guarantees • Usefulness of the checker • Expressiveness • Found subtle bugs in my initial implementation of various optimizations define fact equals(X: Var, E: Expr) with meaning « X == E ¬ if curr. Stmt == [X = E] Æ then “X equals(X, E)@out does not appear in E” then equals(X, E)@out xx : = = xx ++ 11 equals (x , x + 1)

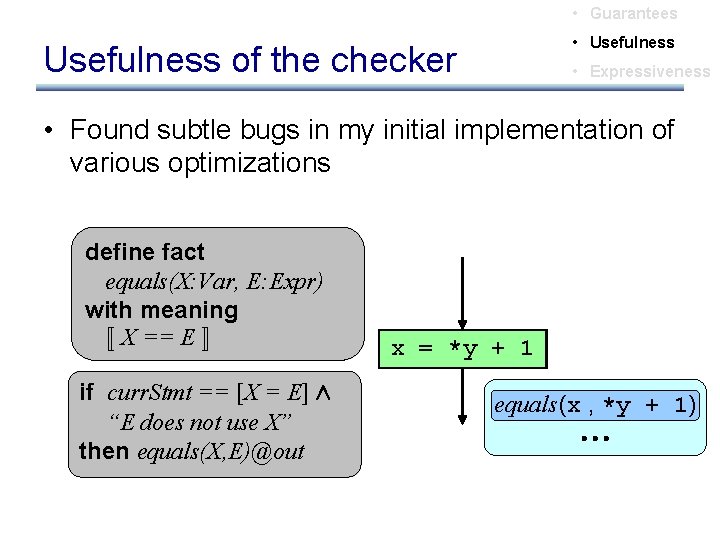
• Guarantees • Usefulness of the checker • Expressiveness • Found subtle bugs in my initial implementation of various optimizations define fact equals(X: Var, E: Expr) with meaning « X == E ¬ if curr. Stmt == [X = E] Æ “X does not use “E appear X” in E” then equals(X, E)@out xx == *y x ++ 11 equals(x (x, , *y x ++ 1) 1)

• Guarantees Rhodium expressiveness • Usefulness • Expressiveness • Traditional optimizations: – const prop and folding, branch folding, dead assignment elim, common sub-expression elim, partial redundancy elim, partial dead assignment elim, arithmetic invariant detection, and integer range analysis. • Pointer analyses – must-point-to analysis, Andersen's may-point-to analysis with heap summaries • Loop opts – loop-induction-variable strength reduction, code hoisting, code sinking • Array opts – constant propagation through array elements, redundant array load elimination

• Guarantees Expressiveness limitations • Usefulness • Expressiveness • May not be able to express your optimization in Rhodium – opts that build complicated data structures – opts that perform complicated many-to-many transformations (e. g. : loop fusion, loop unrolling) • A correct Rhodium optimization may be rejected by the correctness checker – limitations of theorem prover – limitations of first-order logic

Lessons learned (discussion)

Lessons learned (my answers) • Capture structure of problem – Rhodium: flow functions, rewrite rules, prof. heuristics – Restricts the programmer, but can lead to better reasoning abilities – Split correctness-critical code from rest • Split verification task – meta-level vs. per-verification – between analysis tool and theorem prover – between human and theorem prover

Lessons learned (my answers) • DSL design is an iterative process – Hard to see best design without trying something first • Previous version of Rhodium was called Cobalt – Cobalt was based on temporal logic – Stepping stone towards Rhodium

Lessons learned (my answers) • One of the gotchas is efficient execution – easier to reason about automatically does not always mean easier to execute efficiently – can possibly recover efficiency with hints from users – how can you trust a complex execution engine? • Rely on annotations? – meanings in Rhodium – May be ok, especially if annotations simply state what the programmer is already thinking

Conclusion • Rhodium system – makes it easier to write optimizations – provides correctness guarantees – is expressive enough for realistic optimizations • Rhodium is an example of using a DSL to allow more precise reasoning