Pohyby v centrlnm poli Uvaujme pohyby v centrlnm

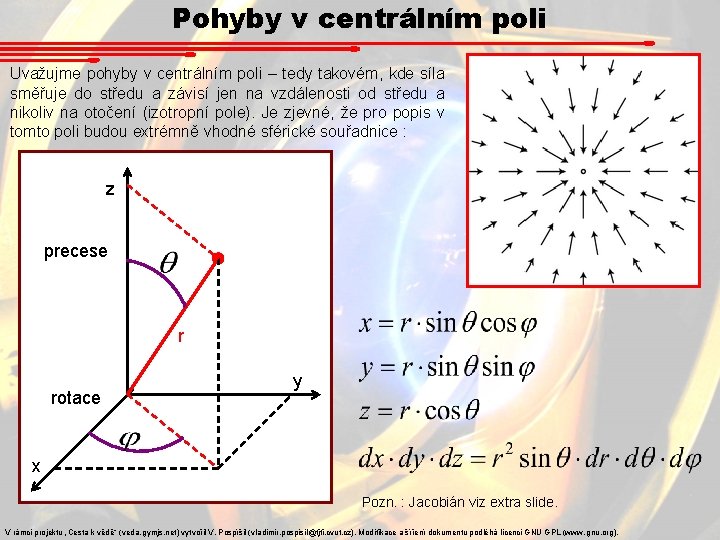
Pohyby v centrálním poli Uvažujme pohyby v centrálním poli – tedy takovém, kde síla směřuje do středu a závisí jen na vzdálenosti od středu a nikoliv na otočení (izotropní pole). Je zjevné, že pro popis v tomto poli budou extrémně vhodné sférické souřadnice : z precese r rotace y x Pozn. : Jacobián viz extra slide. V rámci projektu „Cesta k vědě“ (veda. gymjs. net) vytvořil V. Pospíšil (vladimir. pospisil@fjfi. cvut. cz). Modifikace a šíření dokumentu podléhá licenci GNU GPL (www. gnu. org).

Pohyby v centrálním poli Síla míří vždy směrem do centra (se kterým spojíme počátek vztažné soustavy), je tedy rovnoběžná s polohovým vektorem. Zaveďme dvě nové veličiny, které popisují rotační pohyb kolem nějakého středu. Jsou to z p Moment síly F Moment hybnosti r rotace x y Tyto veličiny jsou samozřejmě definované obecně, nejen pro centrální pole. Udávají, jak moc se síla resp. hybnost podílí na rotačním pohybu. Je zjevné, že moment síly je pro centrální pole nulový – vektorový součin dvou rovnoběžných vektorů je nula. Působící síla tedy neudílí hmotnému bodu rotaci kolem středu.

Pohyby v centrálním poli Oproti tomu moment hybnosti je obecně nenulový, ale pro jeho derivaci platí : z p F r rotace x y a tedy Fakt, že moment hybnosti se zachovává (je konstantní v čase) má závažné důsledky : je-li směr vektoru l konstantní, pak r i p jsou stále kolmé na jeden pevně daný směr a to znamená, že se pohybují v rovině. Částice v izotropním centrálním poli tedy vykonává vždy rovinný pohyb. Pozn. : pro planety této rovině říkáme rovina ekliptiky.

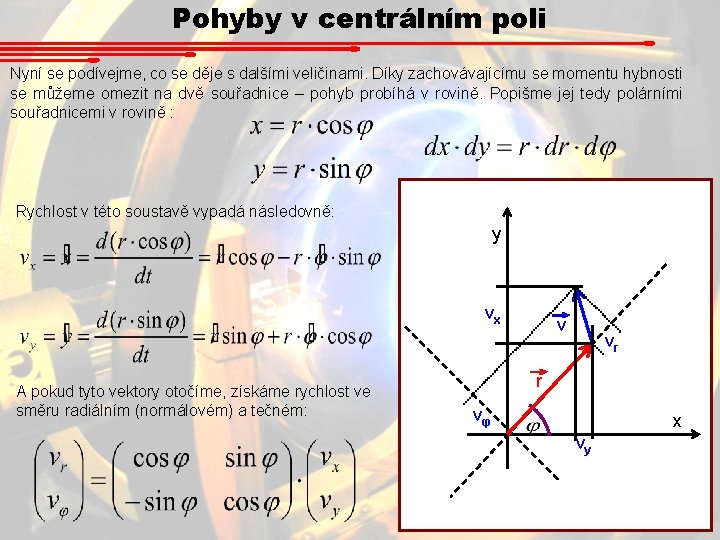
Pohyby v centrálním poli Nyní se podívejme, co se děje s dalšími veličinami. Díky zachovávajícímu se momentu hybnosti se můžeme omezit na dvě souřadnice – pohyb probíhá v rovině. Popišme jej tedy polárními souřadnicemi v rovině : Rychlost v této soustavě vypadá následovně: y vx A pokud tyto vektory otočíme, získáme rychlost ve směru radiálním (normálovém) a tečném: v vr r vφ x vy

Pohyby v centrálním poli Dosadíme : Tedy Rychlost vzdalování/přibližování HB od středu Rychlost pohybu HB po kružnici s poloměrem r (ω je úhlová rychlost). Kvadrát velikosti vektoru rychlosti Pozn. : Na rozdíl od jednoduchého pohybu po kružnici zde jak r, tak ω jsou funkcemi času!

Pohyby v centrálním poli Zrychlení se spočítá obdobně: Normálové (radiální) zrychlení Tečné zrychlení

Pohyby v centrálním poli Pohyb je vykonáván v rovině kolmé na moment hybnosti. Velikost momentu hybnosti je ale také konstantní a musí platit Nuly na z-tových souřadnicích vyjadřují, že HB se drží v jedné rovině, kterou jsme si pro tento výpočet představili jako rovinu XY. Pozor, tato rovnice by neplatila bez absolutních hodnot, směr momentu hybnosti je jinak zcela obecný! Dopočítejme: Veličina se tedy zachovává. Absolutní hodnotu můžeme pominout – veličina se zachovává při pohybu jak po směru, tak proti směru hodinových ručiček a znaménka nemění (pohyb nemůže jen tak změnit směr). Po kratším zamyšlení zjistíme, že toto je vlastně Keplerův zákon o stálé plošné rychlosti planety.

Pohyby v centrálním poli Johannes Kepler 1571 - 1630 Planety se pohybují po elipsách a platí, že za stejný čas T urazí planeta takovou dráhu, že obsah plochy uzavřené elipsou a spojnicemi se sluncem je konstantní.

Pohyby v centrálním poli Víme, že velikost vektorového součinu je číselně rovna velikosti plochy rovnoběžníku, určenému vektory v součinu. Vezmeme-li tedy infinitezimální úhel dφ, určující posun dr (který můžeme považovat za úsečku), dostáváme Časová derivace plochy je potom Plocha se tedy vyvíjí v čase lineárně, což je jen trochu přeformulované tvrzení, že za stejnou dobu je plocha opsaná planetou vždy stejná :

Pohyby v centrálním poli Prozkoumejme nyní, jak vypadá potenciální energie v izotropním centrálním poli. Síla směřuje vždy do středu a její velikost závisí pouze na vzdálenosti r. Potom ale musí platit, že Síla je tedy potenciální a existuje pro ni potenciální energie ve formě funkce jedné proměnné: Pohybové rovnice pak vypadají takto: Už na první pohled působí dojmem neřešitelnosti . Na druhou stranu si můžeme pomoct tím, že známe dvě zachovávající se veličiny : energii a moment hybnosti.

Pohyby v centrálním poli Povšimněme si blíže výrazu pro energii. Druhý výraz v závorce lze upravit na což je ale funkce závislá výhradně na r a lze ji spojit s potenciální energií : Nyní je do efektivní potenciální energie Uef zahrnuta i energie rotačního pohybu a kinetická se redukuje na energii vzdalování resp. přibližování k centru.

Pohyby v centrálním poli Místo složitých pohybových rovnic tak můžeme vyjít s výrazu pro energii Provést separaci proměnných (což pro naše praktické účely znamená formálně „vynásobit“ výraz diferenciálem dt a upravit: a obě strany zvlášť zintegrovat – levou podle t a pravou podle r : Tak získáme čas jako funkci vzdálenosti od centra a dopočítáme inverzní funkci r(t). Obdobný integrál bychom dostali pro φ. Pro konkrétní případ je samozřejmě nutné znát konkrétní podobu funkce Uef a hodnotu celkové energie E.

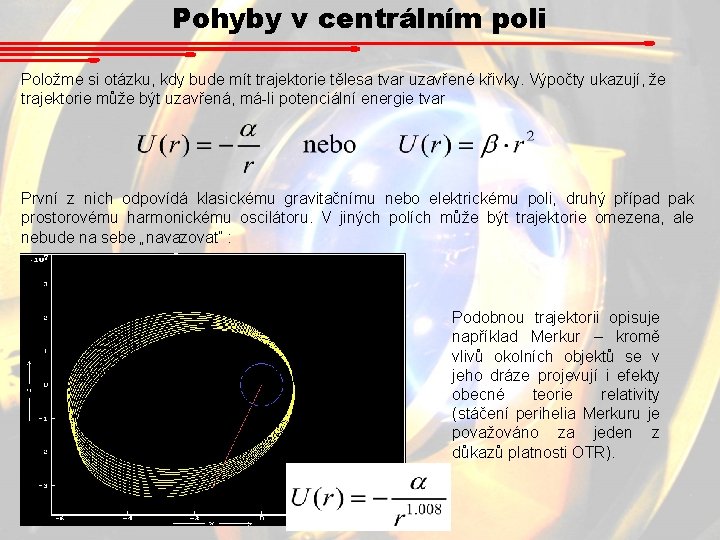
Pohyby v centrálním poli Položme si otázku, kdy bude mít trajektorie tělesa tvar uzavřené křivky. Výpočty ukazují, že trajektorie může být uzavřená, má-li potenciální energie tvar První z nich odpovídá klasickému gravitačnímu nebo elektrickému poli, druhý případ pak prostorovému harmonickému oscilátoru. V jiných polích může být trajektorie omezena, ale nebude na sebe „navazovat“ : Podobnou trajektorii opisuje například Merkur – kromě vlivů okolních objektů se v jeho dráze projevují i efekty obecné teorie relativity (stáčení perihelia Merkuru je považováno za jeden z důkazů platnosti OTR).

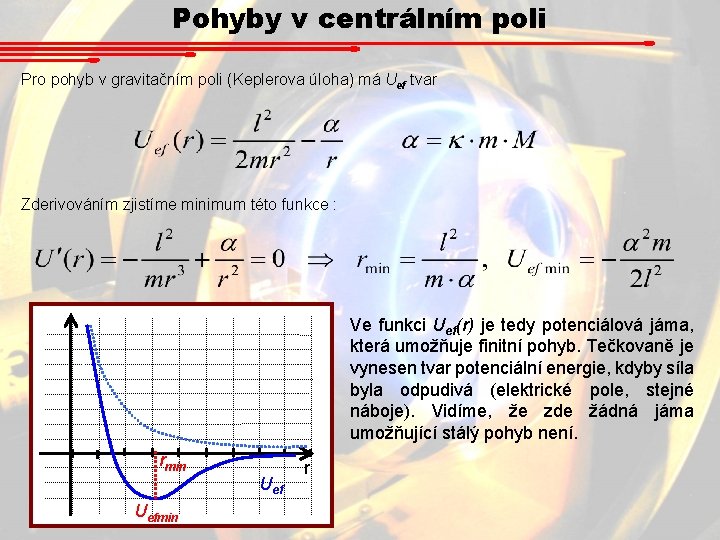
Pohyby v centrálním poli Pro pohyb v gravitačním poli (Keplerova úloha) má Uef tvar Zderivováním zjistíme minimum této funkce : Ve funkci Uef(r) je tedy potenciálová jáma, která umožňuje finitní pohyb. Tečkovaně je vynesen tvar potenciální energie, kdyby síla byla odpudivá (elektrické pole, stejné náboje). Vidíme, že zde žádná jáma umožňující stálý pohyb není. rmin Uef r

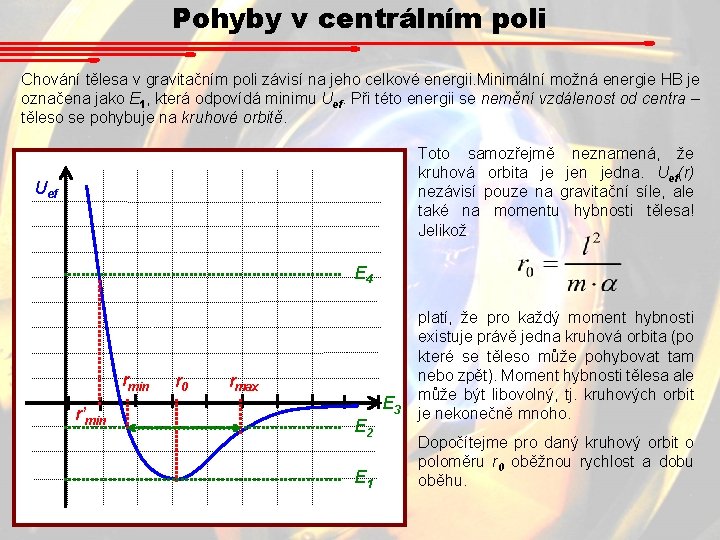
Pohyby v centrálním poli Chování tělesa v gravitačním poli závisí na jeho celkové energii. Minimální možná energie HB je označena jako E 1, která odpovídá minimu Uef. Při této energii se nemění vzdálenost od centra – těleso se pohybuje na kruhové orbitě. Toto samozřejmě neznamená, že kruhová orbita je jen jedna. Uef(r) nezávisí pouze na gravitační síle, ale také na momentu hybnosti tělesa! Jelikož Uef E 4 rmin r’min r 0 rmax E 2 E 1 E 3 platí, že pro každý moment hybnosti existuje právě jedna kruhová orbita (po které se těleso může pohybovat tam nebo zpět). Moment hybnosti tělesa ale může být libovolný, tj. kruhových orbit je nekonečně mnoho. Dopočítejme pro daný kruhový orbit o poloměru r 0 oběžnou rychlost a dobu oběhu.

Pohyby v centrálním poli Gravitační konstanta je součástí Newtonova gravitačního zákona a její hodnota je dopočítána z pozorovaných pohybů planet. Dosaďme do kruhového orbitu za moment hybnosti a vyjádřeme rychlost: tj. pro rychlost platí Jednotky sedí, vzorec vypadá O. K. A jelikož délka kruhového orbitu o poloměru r 0 je 2πr 0, potom Rozměrovou analýzu proveďte sami. Vidíme, že jak oběžná rychlost, tak doba oběhu nezávisí na hmotnosti tělesa, což je v souladu s pozorováním i se „zdravým selským rozumem“ (ZSR). Příklad Spočítejte výšku geostacionární oběžné dráhy nad povrchem země. Mz = 5, 9736× 1024 kg

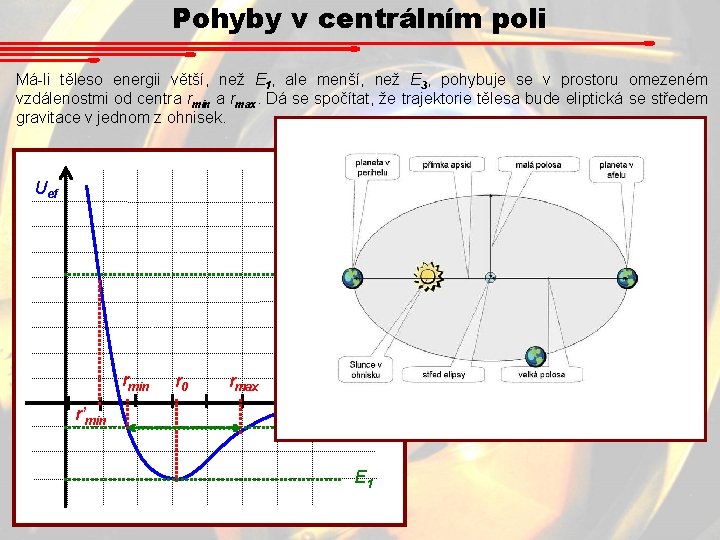
Pohyby v centrálním poli Má-li těleso energii větší, než E 1, ale menší, než E 3, pohybuje se v prostoru omezeném vzdálenostmi od centra rmin a rmax. Dá se spočítat, že trajektorie tělesa bude eliptická se středem gravitace v jednom z ohnisek. Uef E 4 rmin r’min r 0 rmax E 2 E 1 E 3

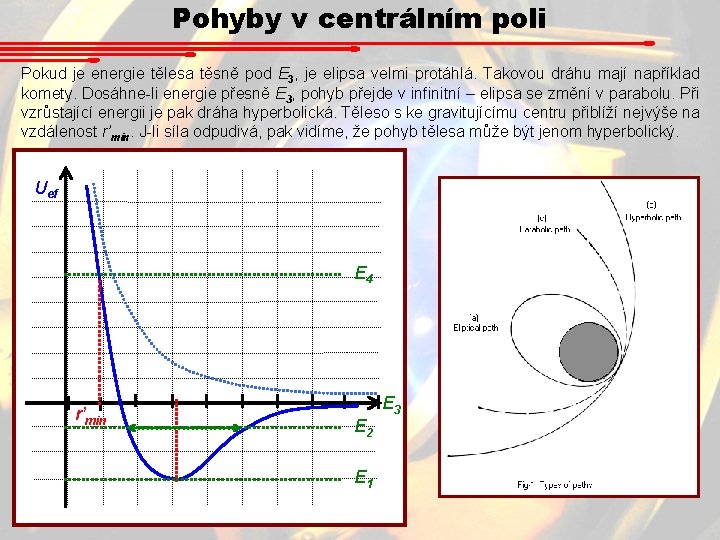
Pohyby v centrálním poli Pokud je energie tělesa těsně pod E 3, je elipsa velmi protáhlá. Takovou dráhu mají například komety. Dosáhne-li energie přesně E 3, pohyb přejde v infinitní – elipsa se změní v parabolu. Při vzrůstající energii je pak dráha hyperbolická. Těleso s ke gravitujícímu centru přiblíží nejvýše na vzdálenost r’min. J-li síla odpudivá, pak vidíme, že pohyb tělesa může být jenom hyperbolický. Uef E 4 r’min E 2 E 1 E 3

Kosmické rychlosti Udělíme-li tělesu v nějaké výšce nad povrchem Země (kterou aproximujeme gravitujícím bodem) počáteční rychlost, může nastat několik možností: a) Rychlost je nízká, těleso se pohybuje po elipse tak, že dopadá na povrch. Pro nás nezajímavé. b) Rychlost je taková, že se těleso pohybuje po kruhové dráze a vrátí se do původního bodu. Pokud je výška nad povrchem zanedbatelná, dosáhli jsme 1. kosmické rychlosti 7, 912 km. s-1. Jedná se vlastně o kruhovou rychlost kolem Země ve výšce r 0 = 6378 m 1). c) Při vzrůstající rychlosti se těleso stále vrací do původního bodu, pohybuje se ale po více a více protáhlejších elipsách. d) Těleso se již nevrátí – dosáhlo rychlosti potřebné pro parabolickou dráhu. Této rychlosti, která má pro Zemi hodnotu 11, 18 kms-1 a pro Slunce 42, 1 kms-1 říkáme 2. kosmická rychlost nebo také úniková. e) Rychlosti, kterou je tělesu třeba udělit, aby opustilo nejen Zemi, ale i Sluneční soustavu, se říká 3. kosmická a má velikost 16. 6 kms-1. Takto nízká je díky rychlosti Země kolem Slunce. 1) Abychom si vybavili toto číslo, stačí si v duchu říct „Šetři se, osle!“

Pohyby v neinerciální soustavě Neinerciální soustavu lze popsat jako inerciální, pokud do ní vneseme vnější, setrvačné síly. Takové síly působí na všechna tělesa v soustavě a nelze jim přisoudit žádného původce. Pokud jedoucí autobus prudce zabrzdí nebo do něčeho narazí, začne na pasažéry působit značně velká síla, která je vrhne vpřed po směru jízdy. Z hlediska vztažné soustavy autobusu ji nelze nijak vysvětlit. Rakouský fyzik E. Mach se pokusil existenci setrvačných sil vysvětlit celkovým rozložením hmoty ve vesmíru (tzv. Machův princip). V denní praxi však tuto sílu přisuzujeme spíše neobratnosti řidiče než působení vzdálených galaxií. Ernst Mach 1838 - 1916

Pohyby v neinerciální soustavě Pokud se soustava S 2 pohybuje vůči soustavě S 1 se zrychlením, souřadné osy však zůstávají ve svém směru (žádná ze soustav nerotuje), je snadné systém popsat. Do pohybových rovnic v soustavě S 2 zaneseme zrychlení transformací : z 1 S 1 y 1 z 2 y 2 A S 2 x 1 x 2 V neinerciální soustavě S 2 se tak v pohybové rovnici objeví další síla, odpovídající Fs = -m. A :

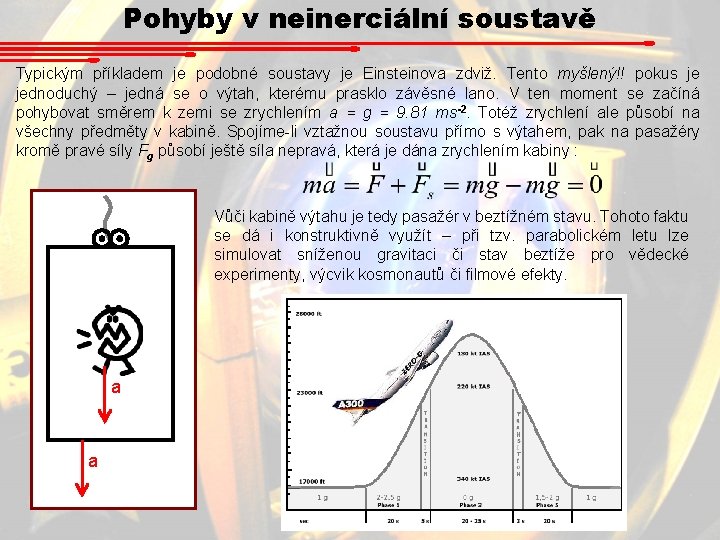
Pohyby v neinerciální soustavě Typickým příkladem je podobné soustavy je Einsteinova zdviž. Tento myšlený!! pokus je jednoduchý – jedná se o výtah, kterému prasklo závěsné lano. V ten moment se začíná pohybovat směrem k zemi se zrychlením a = g = 9. 81 ms-2. Totéž zrychlení ale působí na všechny předměty v kabině. Spojíme-li vztažnou soustavu přímo s výtahem, pak na pasažéry kromě pravé síly Fg působí ještě síla nepravá, která je dána zrychlením kabiny : Vůči kabině výtahu je tedy pasažér v beztížném stavu. Tohoto faktu se dá i konstruktivně využít – při tzv. parabolickém letu lze simulovat sníženou gravitaci či stav beztíže pro vědecké experimenty, výcvik kosmonautů či filmové efekty. a a

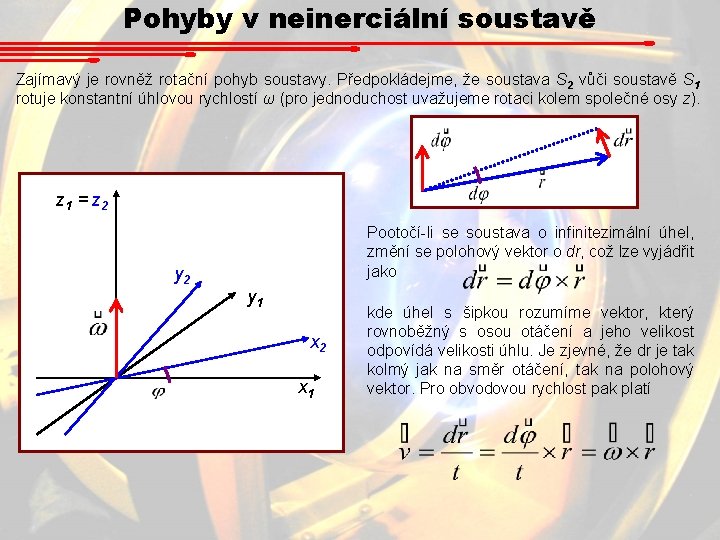
Pohyby v neinerciální soustavě Zajímavý je rovněž rotační pohyb soustavy. Předpokládejme, že soustava S 2 vůči soustavě S 1 rotuje konstantní úhlovou rychlostí ω (pro jednoduchost uvažujeme rotaci kolem společné osy z). z 1 = z 2 y 2 Pootočí-li se soustava o infinitezimální úhel, změní se polohový vektor o dr, což lze vyjádřit jako y 1 x 2 x 1 kde úhel s šipkou rozumíme vektor, který rovnoběžný s osou otáčení a jeho velikost odpovídá velikosti úhlu. Je zjevné, že dr je tak kolmý jak na směr otáčení, tak na polohový vektor. Pro obvodovou rychlost pak platí

Pohyby v neinerciální soustavě Nyní předpokládejme, že se těleso v rotující soustavě pohybuje (běžíme na kolotoči, pohybujeme se po povrchu rotující Země). Pohrajeme-li si s vektory a vektorovými součiny, zjistíme, že v rotující soustavě působí dvě setrvačné síly : odstředivá síla Coriolisova síla Známý příklad – házení míčů Lochneské dráze. Zasáhnout koš velmi obtížné, neboť na pohybující míč působí Coriolisova síla, která vychyluje z dráhy. na je se jej Nad touto silou se lze zamyslet i jinak. Při pohybu od okraje kotouče do středu se mění obvodová rychlost – tj. na těleso působí zrychlení a tedy síla.

Mechanika soustavy těles Sledujme nyní soustavu hmotných bodů. Mějme celkem n částic, z nichž každá má svůj polohový vektor, hmotnost, hybnost a rychlost : Předpokládejme, že soustava, v níž částice studujeme, je inerciální, tedy v ní působí jen pravé síly. Ty mohou mít původ v nějakém poli (externí síly) a nebo částice mohou působit silově mezi sebou navzájem (interní síly). Pokud vnější síly na částice nepůsobí, je soustava izolovaná. Pro pravé síly platí Newtonovy zákony. Celkovou sílu, která působí na jednotlivou i-tou částici, lze rozepsat jako kde Fij je síla působící mezi částicemi i a j a kde zřejmě platí, že Fii = 0. Pohybovou rovnici pro částici i pak lze zapsat jako

Mechanika soustavy těles Těchto rovnic je celkem n : Udělejme s nimi teď „špinavý trik“ – všechny tyto rovnice sečteme : Nyní lze provést několik elementárních úprav : kde P je celková hybnost soustavy a F vnejsi celková vnější síla. Nyní si uvědomme, že díky zákonu akce a reakce se všechny vnitřní síly v součtu vykompenzují, neboť Fij = -Fji. Dvojitá suma je tedy vlastně nulová a zůstává nám zákon o změně celkové hybnosti: Změna celkové hybnosti je rovna výslednici vnějších sil 1. věta impulzová

Mechanika soustavy těles Změna celkové hybnosti je rovna výslednici vnějších sil 1. věta impulzová Pokud na soustavu nepůsobí žádné vnější síly, je derivace P nulová a celková hybnost je tedy konstantní – zachovává se v čase. Zkoumejme nyní, jak se změní celková hybnost systému částic, přejdeme-li k jiné inerciální soustavě, která se vzhledem k té původní pohybuje s rychlostí V : kde M je celková hmotnost všech částic v systému. Položíme-li P’ = 0, tj. přejdeme do soustavy, ve které je celková hybnost nulová, získáme rovnost

Mechanika soustavy těles Podíváme-li se na zlomek se sumami pozorně, zjistíme, že se vlastně jedná o vážený průměr – průměrná poloha vážená hmotností částice. To a předchozí výpočty nás opravňují k tvrzení, že v každé soustavě částic existuje význačný bod, ve kterém je jakoby soustředěna celá hmotnost systému. Vnější síly pak mění rychlost a tudíž hybnost tohoto bodu. Také je zjevné, že nepůsobí -li na částice žádné vnější síly, rychlost tohoto bodu se zachovává. Bod nazýváme těžištěm. Těžiště systému částic Vztažné soustavě, ve které platí, že celková hybnost je nulová a která je tedy pevně spojena s těžištěm systému částic, se říká těžišťová soustava. Matematické výpočty jsou v ní obvykle jednodušší, než v jiných.

Mechanika soustavy těles Prozkoumejme další aspekt. Každou jednotlivou pohybovou rovnici vynásobme vektorově zleva polohovým vektorem a opět je všechny sečtěme : Levou stranu upravíme podle věty o součinu derivace : Výsledek je povědomý, a pokud označíme li = ri x pi, pak nula, vektory jsou rovnoběžné pak levá strana je zjevně rovna časové derivaci celkového momentu hybnosti systému částic.

Mechanika soustavy těles Na pravé straně sečtených rovnic je nula, síla působí podél spojnice obou částic, a to je právě ri-rj Vyšlo nám tedy Změna celkového momentu hybnosti je rovna výslednici momentů vnějších sil 2. věta impulzová Jsou-li vnější síly nebo jejich celkový moment nulový, celkový moment hybnosti se zachovává.

Mechanika soustavy těles Zabývejme se nyní energií systému částic. Vynásobme každou z pohybových rovnic skalárně rychlostí a opět je sečtěme : Levou stranu upravme pomocí vztahu pro derivaci složené funkce: a vidíme, že celá levá strana je vlastně derivace celkové kinetické energie podle času.

Mechanika soustavy těles Pravou stranu upravíme následovně : zde nás zajímá jen celková síla působící na částici kde Q jsme označili celkový výkon vnějších sil. Předpokládejme dále, že všechny vnitřní síly jsou potenciální (pokud ne, tak jsme s výpočty skončili). Potenciální energie soustavy je ale funkcí všech souřadnic všech částic : a platí, že Po dosazení

Mechanika soustavy těles Získali jsme tedy rovnost kterou upravíme na tedy celkový výkon vnějších sil je roven změně celkové energie systému částic. Je-li systém izolovaný a Q = 0, pak se celková energie soustavy zachovává a platí Přejděme nyní k jiné vztažné soustavě : V těžišťové soustavě (P’=0) je pak , tj. kinetická energie lze rozložit do energie pohybu částic vůči sobě a energie pohybu systému jako celku.

Mechanika soustavy těles Odvodili jsme si tedy zákony zachování pro celkem deset veličin : • 3 souřadnice celkové hybnosti • 3 souřadnice celkového momentu hybnosti • 3 souřadnice celkové rychlosti těžiště • 1 skalární veličina celkové energie Lze ukázat, že tyto zákony souvisejí s vlastnosti prostoru a času, a to z. z. hybnosti souvisí s homogenitou prostoru (symetrie vůči posunu – vlastnosti prostoru se při posunu nemění ) z. z. momentu hybnosti souvisí s izotropií prostoru (symetrie vůči rotaci – vlastnosti prostoru se při rotaci nemění ) z. z. momentu hybnosti souvisí se symetrií prostoru vůči přechodu mezi vztažnými soustavami (Galileiho transformace) z. z. energie souvisí s homogenitou času (symetrie vůči posunu v čase – fyzikální zákony se nemění, pokud je pozorujeme dříve či později )

Mechanika soustav - Raketová rovnice Země je kolébka lidstva, člověk ale nemůže v kolébce zůstat věčně. Konstantin Eduardovč Ciolkovskij 1857 -1935 Ruský vědec, teoretik kosmických letů. Propočítal mnohé aspekty kosmické mechaniky s ohledem na možnost cestování vesmírem. Jako první navrhl myšlenku kosmického výtahu. Vydal přes 500 prací včetněvědeckofantas-tickýchnovel. Na jeho práci navázal jak Německý raketový program, tak později i Ruský a Americký.

Mechanika soustav - Raketová rovnice Na pohyb rakety je třeba se dívat jako na pohyb systému částic. Jednou z částic (těles) je samotná raketa, další pak částice žhavých plynů, které opouštějí trysku. Celková hybnost soustavy se v daný okamžik musí zachovat a tedy hybnost, se kterou plyny opouští motor získá i samotná raketa – jen v opačném směru. Předpokládejme, že motor kosmické lodi vystřeluje žhavé plyny relativní rychlostí u (rychlost vůči trysce). Spočítejme, jak se raketa chová. Vyjděme nejprve z Newtonova zákona síly a spočítejme změnu hybnosti systému raketa-plyn : změna hmotnosti rakety – palivo ubývá raketa zvýšila rychlost Rovnici upravme A dosaďme do 2. Newtonova zákona : é en l ře st livo y v pa rychlost vystřeleného paliva í dn t o v os pů bn hy

Mechanika soustav - Raketová rovnice Rovnici lze přepsat i do jiného tvaru : Odtud lze vycházet i pro jiné úlohy, například pro pohyb náklaďáku, ze kterého se sype písek. Pak je rychlost u = 0, další výpočet je ale stejný. Předpokládejme nyní, že výslednice vnějších sil je nulová (F = 0) a rychlost výtoku plynů je opačná ke směru letu rakety (raketa je urychlována), tj. . Potom je problém jednorozměrný a Opět díky principu separace proměnných můžeme s diferenciály zacházet jako s čísly a tedy upravíme na tvar Ciolkovského raketová rovnice

Mechanika soustav - Raketová rovnice Provedeme integraci : Za počátečních podmínek v = 0, m = m 0 (startovací hmotnost) získáme a tedy To má pro konstruktéry raket důležitý dopad – maximální rychlost rakety je dána rychlostí výtoku plynů a tedy teplotou spalování (maximum rychlost světla u fotonových pohonů) a poměrem startovací a konečné hmotnosti. Tento poměr má také meze, vždy musí v raketě zůstat alespoň posádka.

Mechanika soustav – Úloha dvou těles Řešit pohybové rovnice dvou těles, které na sebe vzájemně působí, znamená poprat se s řešením soustavy šesti diferenciálních rovnic druhého řádu, kde konkrétní řešení bude záviset na dvanácti integračních konstantách. To zní špatně – naštěstí ale deset z nich máme daných zákony zachování (P, L, V, E). Na obrázku jsou dvě gravitující tělesa. jejich celkovou energii můžeme zapsat jako Dále využijeme zákon zachování celkové hybnosti a těžiště a přesuneme se do těžišťové soustavy :

Mechanika soustav – Úloha dvou těles Označme dále vektor spojující polohy částic a jejich vzájemnou rychlost jako : Potom lze vyjádřit pro polohy a pro rychlosti Energie pak bude

Mechanika soustav – Úloha dvou těles Problém jsme tak převedli na pohyb jednoho tělesa v centrálním poli U(r) s parametry : poloha fiktivního tělesa rychlost fiktivního tělesa hmotnost fiktivního tělesa, tzv. redukovaná hmotnost Úlohu pro jedno těleso už známe a umíme řešit. Polohy a rychlosti v původní soustavě získáme prostým přičtením polohy a rychlosti těžiště: Pozn. : je-li jedno těleso významně těžší, je redukovaná hmotnost skoro rovna jeho hmotnosti a lehčí obíhá kolem něj. Jsou-li tělesa stejně těžká, obíhají kolem společného těžiště. Viz simulace.

Mechanika soustav – Úloha dvou těles Problém jsme tak převedli na pohyb jednoho tělesa v centrálním poli U(r) s parametry : poloha fiktivního tělesa rychlost fiktivního tělesa hmotnost fiktivního tělesa, tzv. redukovaná hmotnost Úlohu pro jedno těleso už známe a umíme řešit. Polohy a rychlosti v původní soustavě získáme prostým přičtením polohy a rychlosti těžiště: Pozn. : je-li jedno těleso významně těžší, je redukovaná hmotnost skoro rovna jeho hmotnosti a lehčí obíhá kolem něj. Jsou-li tělesa stejně těžká, obíhají kolem společného těžiště. Viz simulace.

Mechanika soustav – Úloha tří těles Důležitější úloha pro praktické využití je pohyb tří těles, například Země-Měsíc-raketa. Tento problém je ale analyticky neřešitelný – závislosti poloh na čase pro jednotlivá tělesa nelze vyjádřit jako elementární funkce. Je nutné používat přibližné výpočty – což v reálném čase zvládnou jen počítače. Proto se bez nich kosmické lodi neobejdou – na rychlých výpočtech závisí veškerá kosmická navigace.

Mechanika soustav – Srážky těles Důležitá úloha mechaniky je určit chování dvou částic či těles při časově omezené interakci – srážce. Výpočty srážek se využívají nejenom pro popis dějů v makrosvětě (kulečník), ale zejména v jaderné a subjaderné fyzice, kde jsou srážky částic v podstatě jedinou možností, jak provádět výzkum.

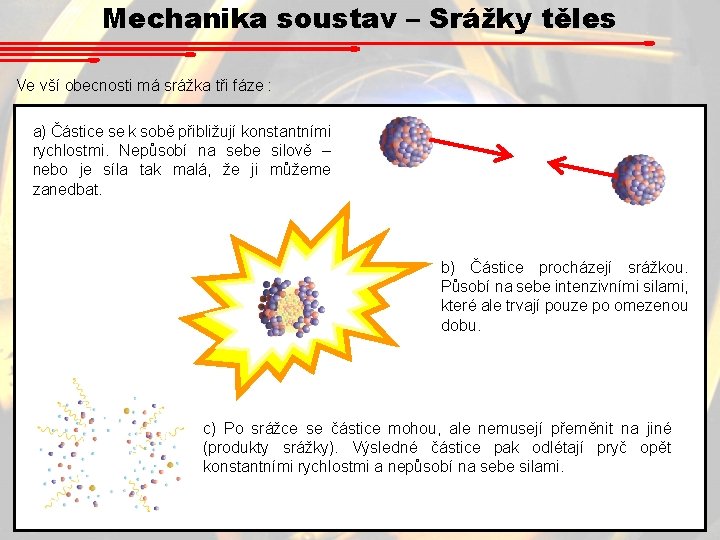
Mechanika soustav – Srážky těles Ve vší obecnosti má srážka tři fáze : a) Částice se k sobě přibližují konstantními rychlostmi. Nepůsobí na sebe silově – nebo je síla tak malá, že ji můžeme zanedbat. b) Částice procházejí srážkou. Působí na sebe intenzivními silami, které ale trvají pouze po omezenou dobu. c) Po srážce se částice mohou, ale nemusejí přeměnit na jiné (produkty srážky). Výsledné částice pak odlétají pryč opět konstantními rychlostmi a nepůsobí na sebe silami.

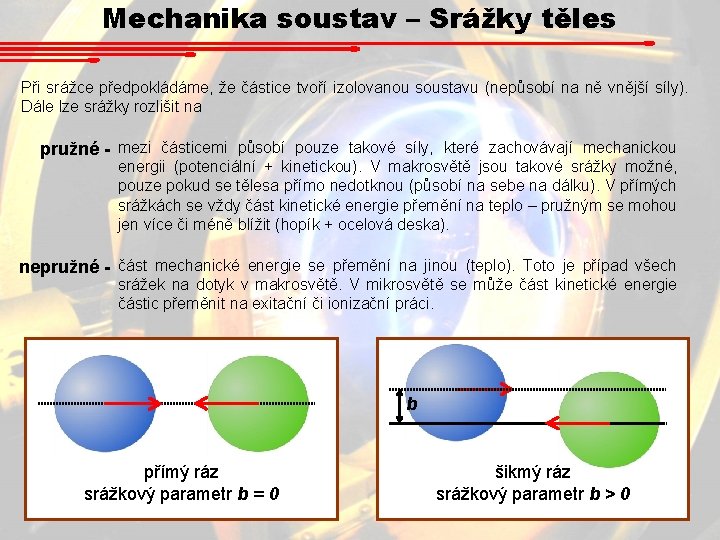
Mechanika soustav – Srážky těles Při srážce předpokládáme, že částice tvoří izolovanou soustavu (nepůsobí na ně vnější síly). Dále lze srážky rozlišit na pružné - mezi částicemi působí pouze takové síly, které zachovávají mechanickou energii (potenciální + kinetickou). V makrosvětě jsou takové srážky možné, pouze pokud se tělesa přímo nedotknou (působí na sebe na dálku). V přímých srážkách se vždy část kinetické energie přemění na teplo – pružným se mohou jen více či méně blížit (hopík + ocelová deska). nepružné - část mechanické energie se přemění na jinou (teplo). Toto je případ všech srážek na dotyk v makrosvětě. V mikrosvětě se může část kinetické energie částic přeměnit na exitační či ionizační práci. b přímý ráz srážkový parametr b = 0 šikmý ráz srážkový parametr b > 0

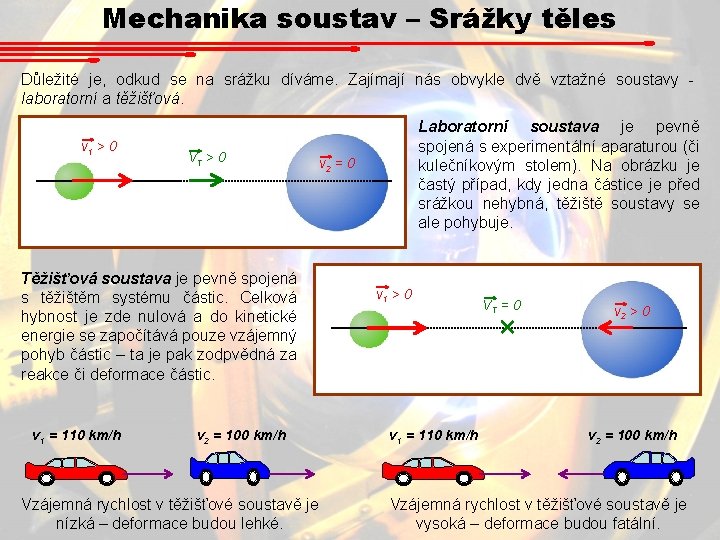
Mechanika soustav – Srážky těles Důležité je, odkud se na srážku díváme. Zajímají nás obvykle dvě vztažné soustavy laboratorní a těžišťová. v 1 > 0 VT > 0 Těžišťová soustava je pevně spojená s těžištěm systému částic. Celková hybnost je zde nulová a do kinetické energie se započítává pouze vzájemný pohyb částic – ta je pak zodpvědná za reakce či deformace částic. v 1 = 110 km/h v 2 = 100 km/h Vzájemná rychlost v těžišťové soustavě je nízká – deformace budou lehké. Laboratorní soustava je pevně spojená s experimentální aparaturou (či kulečníkovým stolem). Na obrázku je častý případ, kdy jedna částice je před srážkou nehybná, těžiště soustavy se ale pohybuje. v 2 = 0 v 1 > 0 v 1 = 110 km/h VT = 0 v 2 > 0 v 2 = 100 km/h Vzájemná rychlost v těžišťové soustavě je vysoká – deformace budou fatální.

Mechanika soustav – Srážky těles Co se děje při během srážky většinou nevíme – při srážkách elementárních částic většinou ani neznáme tvar potenciálu U(r) – ten je obvykle předmětem našeho zkoumání. Z rozdělení kinematických veličin před a po srážce lze do jisté míry odvodit, jaké síly na částice působily. Příklad Na obrázcích máte nakreslené dráhy tvrdých kuliček, které se odrážejí od různých geometrických útvarů. Určete, jaké útvary to jsou. Interakční oblast Toto je v nejhrubších obrysech princip všech experimentů částicové fyziky .

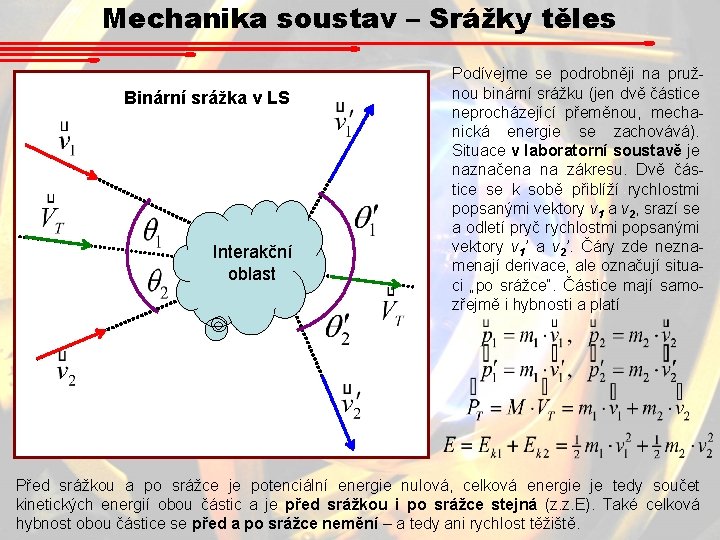
Mechanika soustav – Srážky těles Binární srážka v LS Interakční oblast Podívejme se podrobněji na pružnou binární srážku (jen dvě částice neprocházející přeměnou, mechanická energie se zachovává). Situace v laboratorní soustavě je naznačena na zákresu. Dvě částice se k sobě přiblíží rychlostmi popsanými vektory v 1 a v 2, srazí se a odletí pryč rychlostmi popsanými vektory v 1’ a v 2’. Čáry zde neznamenají derivace, ale označují situaci „po srážce“. Částice mají samozřejmě i hybnosti a platí Před srážkou a po srážce je potenciální energie nulová, celková energie je tedy součet kinetických energií obou částic a je před srážkou i po srážce stejná (z. z. E). Také celková hybnost obou částice se před a po srážce nemění – a tedy ani rychlost těžiště.

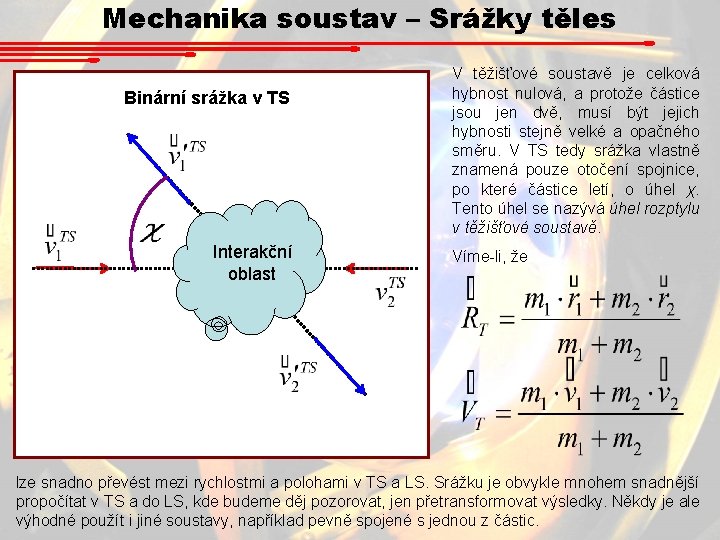
Mechanika soustav – Srážky těles Binární srážka v TS Interakční oblast V těžišťové soustavě je celková hybnost nulová, a protože částice jsou jen dvě, musí být jejich hybnosti stejně velké a opačného směru. V TS tedy srážka vlastně znamená pouze otočení spojnice, po které částice letí, o úhel χ. Tento úhel se nazývá úhel rozptylu v těžišťové soustavě. Víme-li, že lze snadno převést mezi rychlostmi a polohami v TS a LS. Srážku je obvykle mnohem snadnější propočítat v TS a do LS, kde budeme děj pozorovat, jen přetransformovat výsledky. Někdy je ale výhodné použít i jiné soustavy, například pevně spojené s jednou z částic.

Mechanika soustav – Srážky těles Příklad Spočítejte, kolik energie předá jedna částice druhé při pružné binární srážce, je-li jedna z částic před srážkou v klidu. Zkonkrétněte pro případ stejně těžkých částic a ukažte, že probíhá-li srážka po přímce, je předání energie 100%. Ověřte srážením mincí stejné hodnoty. chceme poměr

Mechanika soustav – Srážky těles kde θ je úhel, který spolu svírají vektory v 1 a v’ 2. Podíváme-li se na tuto rovnici pozorně, zjistíme, že z ní plyne rovnost a tedy Pomocí rozměrové analýzy ověřte, že tento výraz má opravdu rozměr energie.

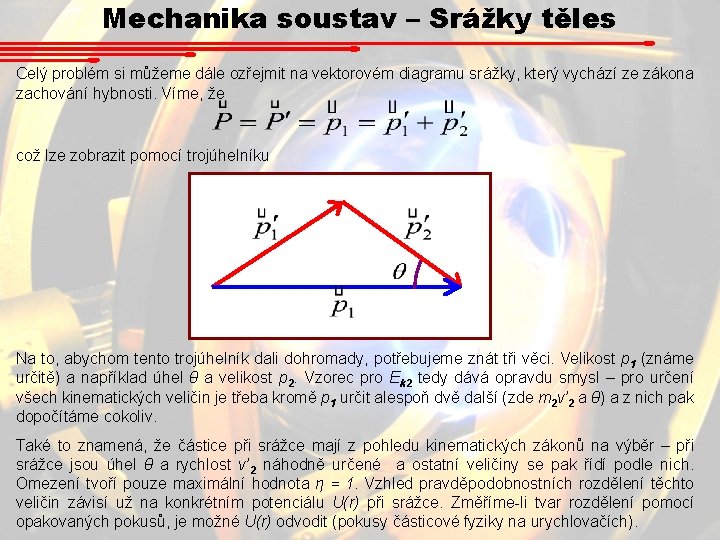
Mechanika soustav – Srážky těles Celý problém si můžeme dále ozřejmit na vektorovém diagramu srážky, který vychází ze zákona zachování hybnosti. Víme, že což lze zobrazit pomocí trojúhelníku Na to, abychom tento trojúhelník dali dohromady, potřebujeme znát tři věci. Velikost p 1 (známe určitě) a například úhel θ a velikost p 2. Vzorec pro Ek 2 tedy dává opravdu smysl – pro určení všech kinematických veličin je třeba kromě p 1 určit alespoň dvě další (zde m 2 v’ 2 a θ) a z nich pak dopočítáme cokoliv. Také to znamená, že částice při srážce mají z pohledu kinematických zákonů na výběr – při srážce jsou úhel θ a rychlost v’ 2 náhodně určené a ostatní veličiny se pak řídí podle nich. Omezení tvoří pouze maximální hodnota η = 1. Vzhled pravděpodobnostních rozdělení těchto veličin závisí už na konkrétním potenciálu U(r) při srážce. Změříme-li tvar rozdělení pomocí opakovaných pokusů, je možné U(r) odvodit (pokusy částicové fyziky na urychlovačích).

Mechanika soustav – Srážky těles Poměr předané energie je tedy a speciálně pro stejně těžké koule Pohybují-li se po přímce, je zjevně θ = 0, ale rychlost v’ 2 už také nebude libovolná. Ze z. z. hybnosti a z. z. energie získáme soustavu rovnic se dvěmi řešeními z nichž první je fyzikálně nezajímavé (ke srážce nedošlo), a druhé znamená, že se první z částic zcela zastavila a celou svou energii (a hybnost) předala druhé.

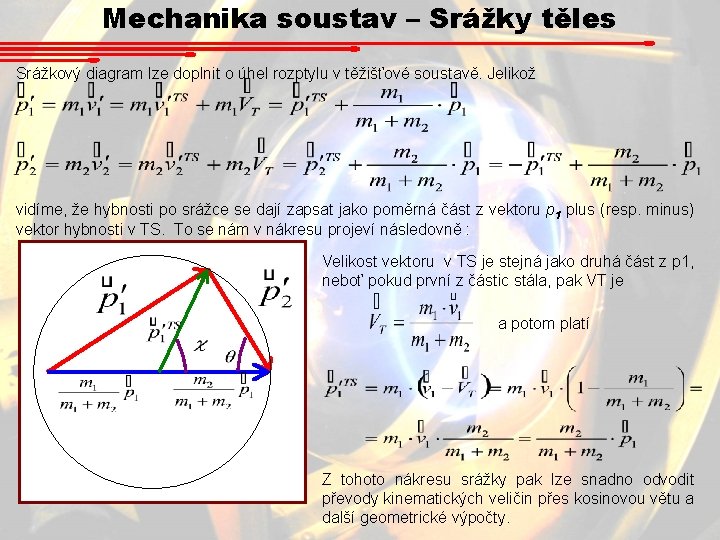
Mechanika soustav – Srážky těles Srážkový diagram lze doplnit o úhel rozptylu v těžišťové soustavě. Jelikož vidíme, že hybnosti po srážce se dají zapsat jako poměrná část z vektoru p 1 plus (resp. minus) vektor hybnosti v TS. To se nám v nákresu projeví následovně : Velikost vektoru v TS je stejná jako druhá část z p 1, neboť pokud první z částic stála, pak VT je a potom platí Z tohoto nákresu srážky pak lze snadno odvodit převody kinematických veličin přes kosinovou větu a další geometrické výpočty.

Mechanika soustav – Srážky těles Příklad Rozeberte případy, kdy těžší částice nalétává na lehčí, lehčí na těžší a kdy jsou částice obě stejné. Nakreslete srážkové diagramy a odvoďte omezení kinematických veličin. Odvoďte vztah mezi rozptylem v těžišťové soustavě a úhly částic v laboratorní soustavě po srážce.

Shrnutí • Pohyby v centrálním poli, obecné řešení v kvadraturách • Pohyby v centrálním gravitačním poli, Keplerovy zákony • Keplerova úloha, trajektorie v gravitačním poli • Kosmické rychlosti • Pohyby v neinerciální soustavě • Mechanika soustavy těles, zákony zachování • Raketová rovnice • Úloha dvou těles • Pružné binární srážky • Srážkový diagram

Jacobián sférické transformace