Podcast Ch 17 c Title Euler Tree Traversal

Podcast Ch 17 c • Title: Euler Tree Traversal • Description: Euler traversal; program 17. 3 • Participants: Barry Kurtz (instructor); John Helfert and Tobie Williams (students) • Textbook: Data Structures for Java; William H. Ford and William R. Topp

Euler Tree Traversal • Up to this point, all of our tree traversal algorithms visit each node exactly once. For instance, the inorder traversal visits the node between visiting the left subtree and the right subtree. • We need a more general tree traversal algorithm for some applications, one that will visit each node more than once. The Euler tour traversal provides a solution.

Euler Tree Traversal (continued) • The Euler tour is a walk around T, encountering each node three times: – On the left, before the Euler tour of the node's left subtree. – From below, as we finish the tour of the left subtree. – On the right, after we finish the Euler tour of the right subtree. – If the node is a leaf, we consider the visits to all occur at once.

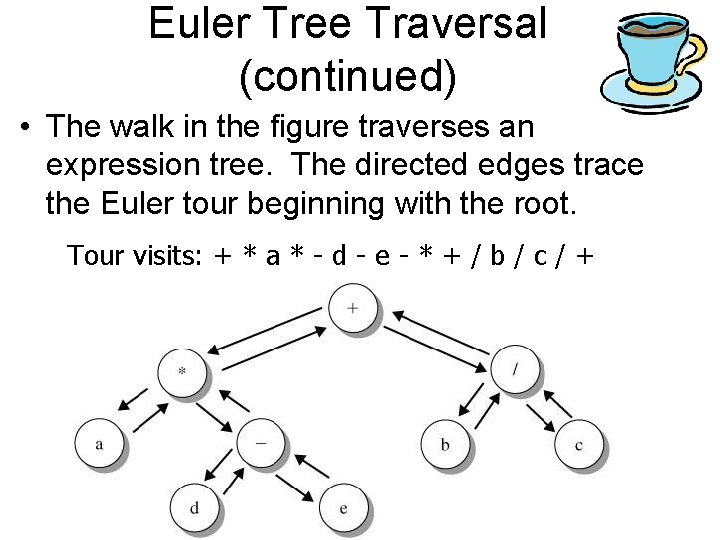
Euler Tree Traversal (continued) • The walk in the figure traverses an expression tree. The directed edges trace the Euler tour beginning with the root. Tour visits: + * a * - d - e - * + / b / c / +

Euler Tree Traversal (continued) Algorithm euler. Tour(TNode t): if t ≠ null if t is a leaf node visit t else visit t // on the left euler. Tour(t. left); visit t; // from below euler. Tour(t. right); visit t; // on the right

Euler Tree Traversal (continued) • Use an Euler tour to generate a fully parenthesized expression from an expression tree. – A visit to an operand inserts the operand in the string. – For an operator, output a "(" for the visit on the left, output the operator for the visit from below, and output a ")" for the visit on the right.

Euler Tree Traversal (concluded) // traverse an expression tree and display the // equivalent fully parenthesized expression public static <T> String full. Paren(TNode<Character> t) { String s = ""; if (t != null) { if (t. left == null && t. right == null) s += t. node. Value; // visit a leaf node else { s += "("; // visit on left s += full. Paren(t. left); s += t. node. Value; // visit from below s += full. Paren(t. right); s += ")"; // visit on right } } return s; }

Program 17. 3 import java. util. Scanner; import ds. util. TNode; import ds. util. Binary. Tree; public class Program 17_3 { public static void main(String[] args) { // prompt for the RPN expression Scanner key. In = new Scanner(System. in); String postfix. Exp; // root of the expression tree TNode<Character> root; System. out. print ("Enter a postfix expresssion: "); postfix. Exp = key. In. next. Line();

Program 17. 3 (concluded) // build the expression tree root = Binary. Tree. build. Exp. Tree(postfix. Exp); // display the tree System. out. println("Expression tree"); System. out. println(Binary. Tree. display. Tree(root, 1)); // output the full parenthesized expression System. out. print("Fully parenthesized expression: "); System. out. println(Binary. Tree. full. Paren(root)); } } Enter a postfix expresssion: a d e - * b c / + Expression tree + * / a b c d e Fully parenthesized expression: ((a*(d-e))+(b/c))

Student Question • Can you think of another application that would benefit from an Euler traversal?