PODATKOVNE STRUKTURE IN ALGORITMI Kaj je algoritem navodilo

PODATKOVNE STRUKTURE IN ALGORITMI

Kaj je algoritem • navodilo, kako opraviti določen postopek • KAJ storiti, KAKO to storiti • točna definicija odvisna od tega, komu je algoritem namenjen • Končno zaporedje ukazov, ki, če jih ubgamo, opravijo neko nalogo

Značilnosti algoritma • • • ima podatke vrne rezultat je natančno določen se vedno konča mogoče ga je opraviti

Vprašanja • Kako zasnovati algoritem metode, strategije • Kako preveriti algoritem dokaz pravilnosti • Kako analizirati algoritem prostorska in časovna zahtevnost • Kako izraziti algoritem enoličnost, komu je namenjen, kaj so osnovna navodila, komentarji

Skupine algoritmov • • • Deli in vladaj Požrešna metoda Sestopanje Dinamično programiranje Razveji in omeji

Skupine algoritmov • • • Sortiranje Algoritmi nad grafi Numerični algoritmi Iskalni algoritmi …

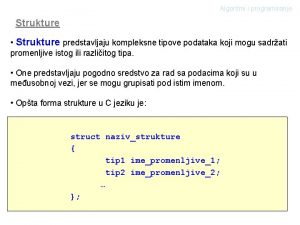
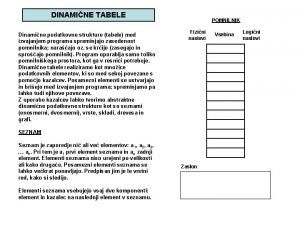
Podatkovne strukture • v programskih jezikih • zaloga vrednosti • operacije • lastnosti operacij • neodvisnost od dejanske predstavitve KAJ je struktura in ne KAKO jo predstaviti

Opis strukture structure ime strukture begin declare opis funkcij where opis aksiomov end

Pomembnejše strukture • • • sklad vrsta drevo tabela graf. . .

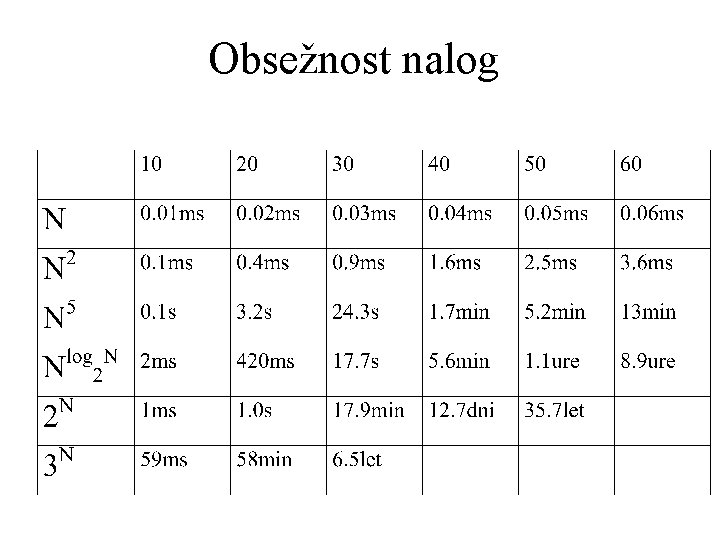
Prostorska in časovna zahtevnost • količina sredstev, ki jih potrebujemo za rešitev problema • odvisnost od obsežnosti (velikosti) problema • kaj meriti • pogosto le ocenimo zahtevnost • red velikosti

Prostorska in časovna zahtevnost • najslabša možnost zgornja meja zahtevnosti • najboljša možnost spodnja meja zahtevnosti • pričakovana zahtevnost • meritve

Časovna zahtevnost • O notacija O(n 2), O(n log(n)), O(2 n) • polinomski algoritmi (P) • razred NP nedeterministični algoritem v polinomskem času • P <> NP ? ? ?

Zakaj je časovna zahtevnost pomembna • • • Urejanje z mehurčki: (n 2 - n)/2 primerjav Vsaka primerjava: 0. 001 sekunde 10 stevil: 0. 05 sek 100 stevil: 5 sek 1000 stevil: 500 sek 100000 stevil (urejamo tel. imenik) 5000000 sek = 1400 ur = slaba dva meseca

Primeri s : = a[1]; for i : = 2 to n do s : = x*s + a[i]; podatki: ai, n, x prostorska zahtevnost časovna zahtevnost po posameznih operacijah

časovna zahtevnost prostorska zahtevnost

dol : = length(niz); je_pali : = true; i : = 1; while (je_pali and (i < dol div 2)) do begin je_pali : = (niz[dol-i+1] = niz[i]); i : = i + 1; } časovna zahtevnost najslabša najboljša pričakovana

Trije algoritmi za isti problem • Dano je zaporedje celih števil a 1, a 2, …, an. Naj bo Si, j = vsota ak, k = i, …, j • Poišči Sopt = maksimalna vsota • 8, -6, 10, -14, 13, -5, 7, -9, 18, -3, 2 rešitev 13, -5, 7, -9, 18 (24)

A- vse vsote! opt : = 0; for i : =1 to n do { i - kje zacnem } for j : = i to n do begin { j - kje neham } s : = a[i]; for k : = i + 1 to j do s : = s + a[k]; if (s > opt) then opt : = s; end;

B - upoštevaj prejšnje vsote Si, j = Si, j-1 + aj opt : = 0; for i : = 1 to n do begin s : = a[i]; if (s > opt) then opt : = s; for j : = i + 1 to n do begin s : = s + a[j]; if (s > opt) then opt : = s; end

C - ali vzamemo zraven j-tega Sj = Sj-1 + aj ali 0 opt : = 0; s : = 0; for i : = 1 to n do begin { i - kje se konca! } t : = s + a[i]; if (t > 0) then { ce je vsota "se > 0, se i-tega splaca vzeti } s : = t else { drugace raje zacnemo na novo } s : = 0; if (s > opt) then opt : = s; end;

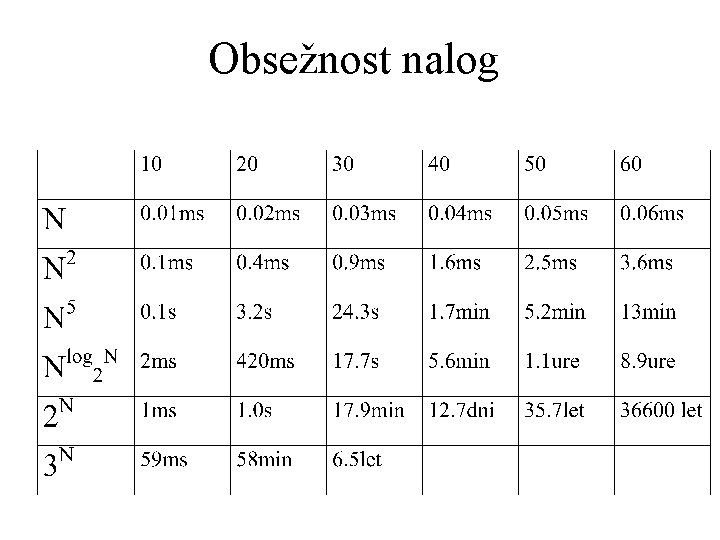
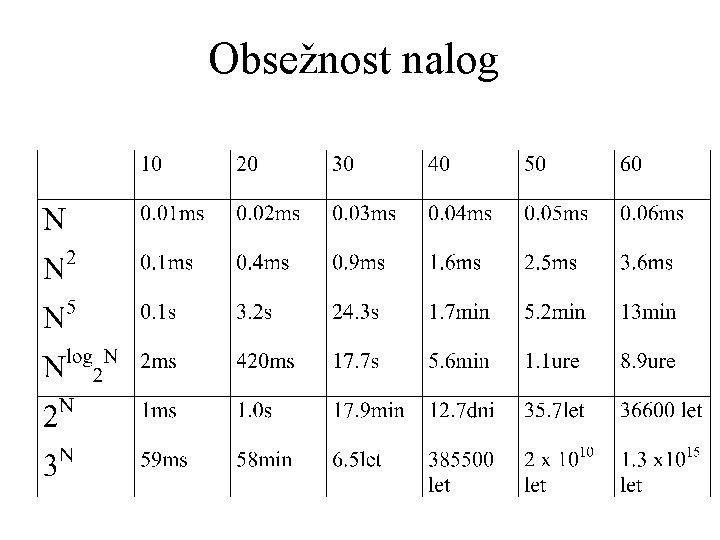
Obsežnost nalog

Obsežnost nalog

Obsežnost nalog

Obsežnost nalog

Obsežnost nalog

Obsežnost nalog

Obsežnost nalog

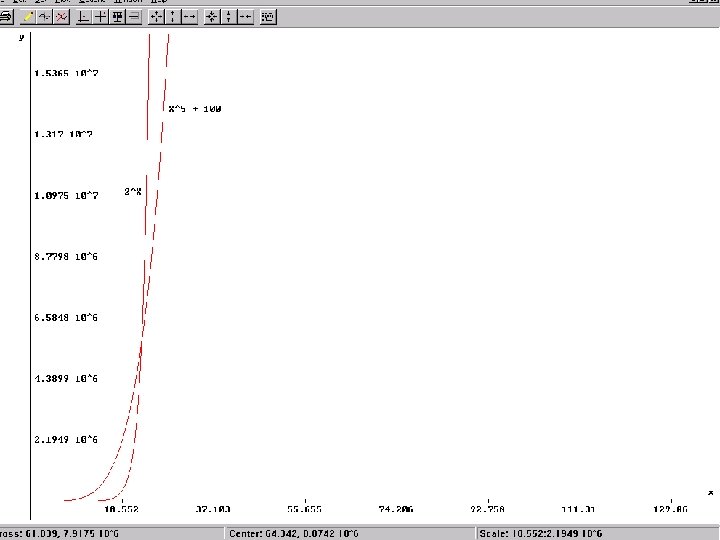
Hitrost računalnika

Hitrost računalnika

Hitrost računalnika

Hitrost računalnika

Hitrost računalnika

Hitrost računalnika

Algoritmi za sortiranje

O sortiranju • Kaj urejamo • Kje so podatki – datoteke – notranji pomnilnik • Različne metode – če vemo za maksimalni podatek: urejanje s koši – vstavljanje, izbiranje, urejanje z mehurčki, urejanje s kopicami, hitro urejanje, zlivanje, . . .

Časovna in prostorska zahtevnost • Kaj štejemo • Pogosto odločilni faktor primerjave: – števila – zapisi/strukture/objekti – slike • Včasih zahtevna zamenjava – zapisi/strukture/objekti – slike

Lastnosti dobrega algoritma za urejanje • pravilnost • hitrost • stabilnost - urejenih elementov ne zamenjuje – več ključev • naravnost - urejene elemente naj uredi hitro – morda predpriprava

5, 2, 11, 7, 9, 36, 45, 1, 24

Urejanje z vstavljanjem • • urejeni del / neurejeni del 2 5 11 : 7 * * * 2 5 7 11 : 9 * * * … • vzemi naslednji element in ga vstavi na pravo mesto

Urejanje z vstavljanjem na vrsti je a-ti elt. pogledamo a-1 tega če je ta manjši od njega, ta-1 prestavimo za eno mesto nazaj pogledamo a-2 ega … mmm_vvvv t : = tabela[a]; b : = a - 1; while (b >= 1 and t < tabela[b]) do begin tabela[b + 1] : = tabela[b]; b : = b - 1; end; tabela[b + 1] : = t;

Urejanje z vstavljanjem procedure vstavljanje(var tabela: tabl; koliko: integer) { { urejanje z vstavljanjem } { urejamo cela stevila } var a, b, t: integer; begin for a : = 2 to koliko do begin t : = tabela[a]; b : = a - 1; { do kam so ze urejeni } while (b >= 1 and t < tabela[b]) do begin { kam spada a-ti } tabela[b + 1] : = tabela[b]; b : = b - 1; end; tabela[b + 1] : = t; end; vstavi. c

Lastnosti • • pravilnost naravnost stabilnost hitrost

Zahtevnost • število primerjav – najboljše • urejeno zaporedje • n - 1 x, na vsakem prehodu: 1 primerjanje • n - 1, Tb = O(n) – najslabše: (n 2+n)/2 - 1 • obratno urejeno • 1 korak: 1 primerjava, 2 korak: 2, …, n-1 (zadnji): n 1 • n(n-1)/2, Tw = O(n 2)

Zahtevnost – povprečno • • zahtevnejša analiza vse možne razporeditve (n 2+n-2)/4 Ta = O(n 2) • število zamenjav – najboljše: 2(n-1) – povprečno: (n 2 + 9 n - 10)/4 – najslabše: (n 2 + 3 n - 4)/2 O(n 2)

Prostorska zahtevnost • O(1) dodatnega prostora

Urejanje z izbiranjem • • • poišči najmanjšega zamenjaj s prvim od 2 do n poišči najmanjšega zamenjaj z drugim. . .

Poišči najmanjšega function poisci_najmanjsega (tab: tabela; od_kje, do_kam: integer): integer; (* poisce najmanjsega v tabeli tab od od_kje dalje *) var i_najm: integer; /* indeks trenutno najmanjsega */ i: integer; begin i_najm : = od_kje; for i : = od_kje + 1 to do_kam do if (tab[i] < tab[i_najm]) then i_najm : = i; poisci_najmanjsega : = i_najm; end;

Končni program procedure izbiranje(var tabela: tab; koliko: integer); (* urejanje z izbiranjem *) (* urejamo cela stevila *) var a, : integer; kje_najm: integer; (* indeks najmanjsega *) for a : = 1 to koliko - 1 do begin kje_najm : = poisci_najmanjsega(tabela, a, koliko); (* zamenjamo *) t : = tabela[a]; tabela[a] : = tabela[kje_najm]; tabela[kje_najm] : = t; end;

Lastnosti • • pravilnost naravnost stabilnost hitrost

Zahtevnost • število primerjav – vedno enako – 1 korak: n - 1 – 2 korak: n - 2 – n - 1 korak: 1 – n*(n-1)/2 primerjav

Zahtevnost • število zamenjav – najboljše • urejeno zaporedje • n -1 elementov premaknemo: 3 • 3 n - 3 – najslabše • n 2/4 + 3(n-1) – povprečno • n(ln n + 0. 577216…) O(n 2)

Urejanje z mehurčki • najlažji element splava na površje • plavanje - zamenjave • 34215 – 34125 – 31425 • 13425 – 13245 • 12345 – 12345 • 12345

Urejanje z mehurčki procedure mehurcki(var tabela: tab; koliko: integer); (* urejanje z mehurcki *) (* urejamo cela stevila *) var a, b: integer; t: integer; begin for a : = 1 to koliko - 1 do for b : = koliko - 1 downto a do if (tabela[b-1] > tabela[b]) then begin (* zamenjamo *) t : = tabela[b-1]; tabela[b-1] : = tabela[b]; tabela[b] : = t; end

Lastnosti • • pravilnost naravnost stabilnost hitrost

Zahtevnost • število primerjav – vedno enako – 1 korak: n - 1 – 2 korak: n - 2 – n - 1 korak: 1 – n*(n-1)/2 primerjav O(n 2)

Zahtevnost • število zamenjav – najboljše • urejeno zaporedje • nobenega ne premaknemo: 0 – najslabše • 3(n 2 -n)/2 – povprečno • 3(n 2 -n)/4 O(n 2)

Urejanje 10000 elementov

Hitro urejanje • Izberi si delilni element • razdeli na dva dela – <=x – >=x • z istim postopkom uredi oba dela

procedure qs_r(var t: tabela; l, d: integer) { (* hitro uredi t od l do d *) (* urejamo cela stevila *) var i, j, x: integer; el: integer; i : = l; j : = d; (* iskalca *) x = t[l]; (* delilni element *) while (i <= j) do begin while (t[i]<x and i<d) do i : = i + 1; (* poisci prvega, ki ni manjsi *) while (t[j]>x and j>l) do j : = j - 1; (* poisci prvega, ki ni vecji *) if (i<=j) then begin (* zamenjaj *) el : = t[i]; t[i] : = t[j]; t[j] : = el; i : = i - 1; j : = j - 1; end; if (l<j) qs_r(t, l, j); (* uredimo levo polovico *) if (i<d) qs_r(t, i, d); (* uredimo desno polovico *) end;

Analiza • zahtevno • pričakovana zahtevnost: O(n log n) • na majhnih zaporedjih običajno nehamo in uporabimo kaj drugega • metoda lahko tudi O(n 2) časa - če delilni element vedno največji • ena najbolj uporabljanih metod