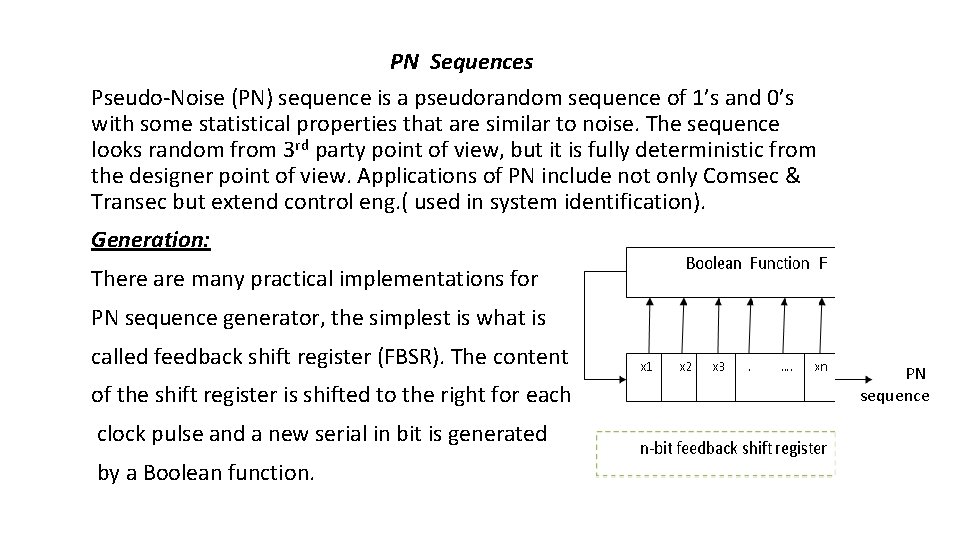
PN Sequences PseudoNoise PN sequence is a pseudorandom

PN Sequences Pseudo-Noise (PN) sequence is a pseudorandom sequence of 1’s and 0’s with some statistical properties that are similar to noise. The sequence looks random from 3 rd party point of view, but it is fully deterministic from the designer point of view. Applications of PN include not only Comsec & Transec but extend control eng. ( used in system identification). Generation: There are many practical implementations for PN sequence generator, the simplest is what is called feedback shift register (FBSR). The content of the shift register is shifted to the right for each clock pulse and a new serial in bit is generated by a Boolean function. PN sequence

Depending on this function, Shift register sequences are Classified into linear and nonlinear FBSR. Linear FBSR: In this case, the Boolean function is the Ex-OR only of some selected taps of the shift register: F(x 1, x 2, x 3, …. . xn)=a 1 x 1+a 2 x 2+x 3 a 3+………. . +anxn Where the +is the mod-2 addition and ai is a binary variable that specifies the taps to be selected. It should be noted, however, that the key K here is the initial content of the register and the feedback taps (a 1, a 2, a 3, …………an). The PN sequence output can be taken from the final stage or any previous stage since the only difference is a time shift. Also, parallel outputs can also be used for other applications. This will give a pseudorandom nonbinary sequence. For linear FBSR, the initial content cannot be all zero state since this will lock the register to the zero state. Depending on the taps (a 1, a 2, a 3, …………an) all statistical properties of the output sequence are determined. Note that there are 2 n different ways to choose the taps but not all of these are useful. Before studying the ways to choose the taps, we will study the statistical properties of the output PN sequence:

N Pmax Taps 3 4 5 6 7 7 15 31 63 127 [1, 3] [3, 4] [2, 5], [2, 3, 4, 5], [1, 2, 4, 5] [1, 6], [1, 2, 5, 6], [2, 3, 5, 6] 8 255 9 10 511 1023 11 2047 [1, 11], [2, 5, 8, 11], ………………. 12 4095 [1, 4, 6, 12], [2, 3, 9, 12], ………………… [1, 7], [3, 7], [1, 2, 3, 7], [2, 3, 4, 7], [2, 4, 6, 7], [1, 3, 6, 7], [2, 5, 6, 7], [1, 2, 4, 5, 6, 7], [1, 2, 3, 4, 5, 7] [2, 3, 4, 8], [3, 5, 6, 8], [2, 5, 6, 8], [1, 3, 5, 8], [1, 5, 6, 8], [1, 6, 7, 8], [1, 2, 5, 6, 7, 8], [1, 2, 3, 4, 6, 8] [4, 9], [3, 4, 6, 9], [4, 5, 8, 9], [1, 4, 8, 9], [2, 3, 5, 9], [5, 6, 8, 9], [2, 7, 8, 9]……. [3, 10], [2, 3, 8, 10], [1, 5, 8, 10]………… In above table, only half of the true taps are given. The 2 nd half can be obtained by subtracting other than an taps from n to obtain the new taps. For example, for n=4, table above gives only [3, 4], the 2 nd set is [4 -3, 4]=[1, 4] and so on. It should be noted, however, that the two PN sequences obtained from the [4, 3] or [4, 1] taps are the same except for a time shift between them.

Example: Generate the linear maximal length PN sequence obtained from the taps[1, 4]. Then find its properties. Q 1 Q 2 Q 3 Q 4 1 1 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 Here F(x)=1+x+x 4 and: Starting with any 4 -bit state ( except zero state), following the sequential generation of each bit in the register, then we notice that the register will repeat itself after 15 clock pulses. Hence, yes, the period is 24 -1=15, and the output sequence is: S(i)=11110101100100011110…… Full period Q 1 Q 2 Q 3 Q 4

To test other properties, then: 0. 5. b-p(00)=3/15, p(01)=4/15, p(10)=4/15, p(11)=4/15≈ 0. 25 almost equal, and so on for run of 3 bits c-Autocorrelation: To find Rss(k) for k=0 to P-1, then cyclically shift S(i) to the right by k and find the no of bits that agrees and no of bits that disagrees, then: Rss(k)=(no of bits that agrees)-(no of bits that disagrees) For k=0, then: 111101011001000 Agree bits=15, disagree bits=0, Rss(0)=15 -0=15 For k=1, then: 111101011001000 011110101100100 Agree bits=7, disagree bits=8, Rss(1)=7 -8=-1 For k=2, then: 111101011001000 001111010110010 Agree bits=7, disagree bits=8, Rss(2)=7 -8=-1, and so on Rss(3)=Rss(4)=……. Rss(14)=-1

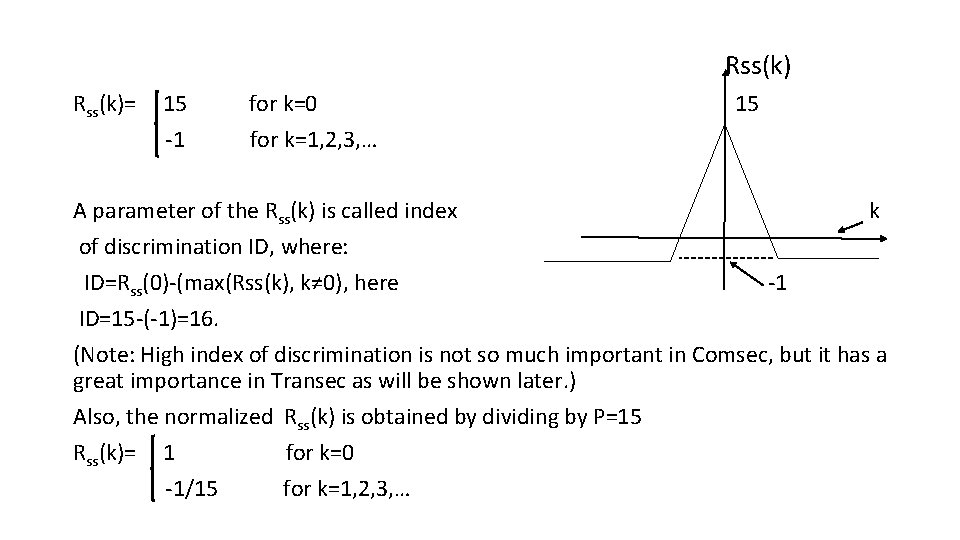
Rss(k)= 15 -1 for k=0 for k=1, 2, 3, … 15 A parameter of the Rss(k) is called index k of discrimination ID, where: ID=Rss(0)-(max(Rss(k), k≠ 0), here -1 ID=15 -(-1)=16. (Note: High index of discrimination is not so much important in Comsec, but it has a great importance in Transec as will be shown later. ) Also, the normalized Rss(k) is obtained by dividing by P=15 Rss(k)= 1 for k=0 -1/15 for k=1, 2, 3, …

Homework 1: For previous example, find Rss(k) if: a-partial period (say half of the period) is used in correlation(partial correlation). b- one error occurred and correlation is carried out over full period. Homework 2: Repeat previous example for non-maximal length sequence obtained using the taps [4, 5]. Linear FBSR as a state machine Let v(i) be a column vector representing the state of the shift register at time i, then: v(i+1)=[A] v(i) mod-2, where [A] is a binary nxn transition matrix representing the taps. The [A] matrix is always of the form with taps written in the 1 st row, 1's just below the main diagonal and 0's elsewhere. For example, if the taps are [1, 4], then:

• MLFBSR period P 1 Non Linear Boolean MLFBSR period P 2 MLFBSR period Pn Function

2 -Complexity: This depends on the choice of the nonlinear Boolean function. It was shown that higher complexity can be obtained if long product terms exist in this function. However, this will produce unbalance in the number of 1's & 0's in the truth table of the nonlinear function resulting in moderate statistical properties of the output sequence. A good compromise can be obtained by computer simulation. 3 -Randomness Properties: This depends on the choice of the nonlinear fn. Sequences with good statistical properties are obtained if the truth table of the fn has a good balance between 0's & 1's. Note: A well-known sequences were suggested and belong to this type, such as Gold codes, JPL codes, Geffe codes and so on. Homework: Prepare simple notes or lecture on Gold codes.

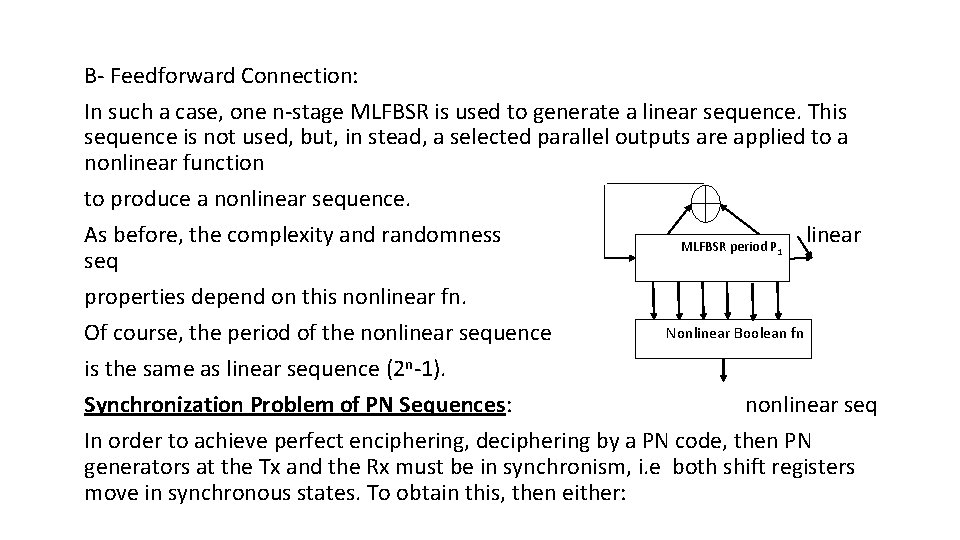
B- Feedforward Connection: In such a case, one n-stage MLFBSR is used to generate a linear sequence. This sequence is not used, but, in stead, a selected parallel outputs are applied to a nonlinear function to produce a nonlinear sequence. As before, the complexity and randomness linear MLFBSR period P seq properties depend on this nonlinear fn. Nonlinear Boolean fn Of course, the period of the nonlinear sequence is the same as linear sequence (2 n-1). Synchronization Problem of PN Sequences: nonlinear seq In order to achieve perfect enciphering, deciphering by a PN code, then PN generators at the Tx and the Rx must be in synchronism, i. e both shift registers move in synchronous states. To obtain this, then either: 1

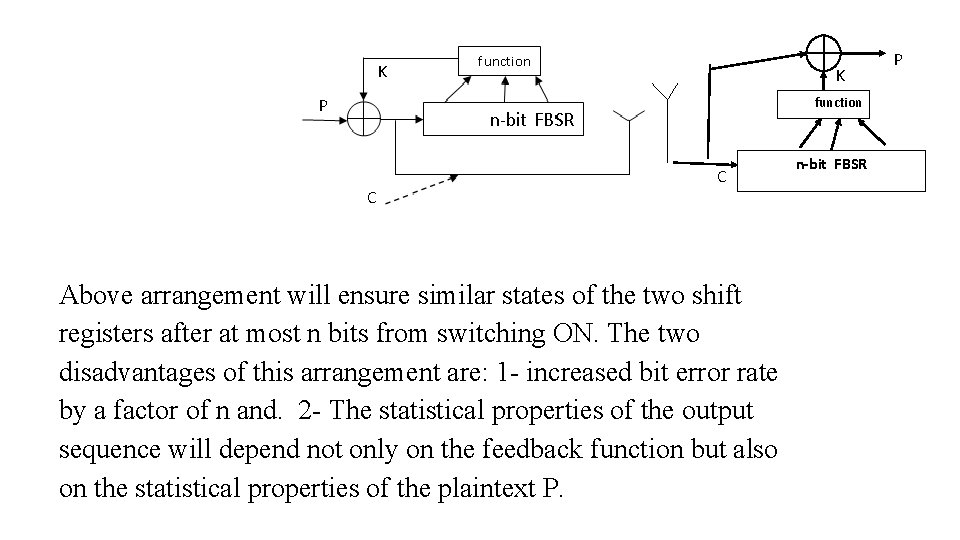
K K function P C C Above arrangement will ensure similar states of the two shift registers after at most n bits from switching ON. The two disadvantages of this arrangement are: 1 - increased bit error rate by a factor of n and. 2 - The statistical properties of the output sequence will depend not only on the feedback function but also on the statistical properties of the plaintext P. n-bit FBSR P