PLUTO a modular code for computational astrophysics Developers

PLUTO: a modular code for computational astrophysics Developers: A. Mignone 1, 2, G. Bodo 2 C. Zanni 3, T. Laverne 2 , F. Rubini 4, S. Massaglia 3, A. Rogava 3, A. Ferrari 3 1 The University of Chicago, ASC FLASH Center 2 INAF Osseratorio Astronomico di Torino 3 Universita’ degli studi di Torino 4 Universita’ degli studi di Firenze

OUTLINE • Written in C ( ~ 33, 000 lines) • Explicit, compressible code (FV): – Shock capturing – High-mach number flows • Works in 1, 2, 3 -D • Modular structure: – – Physics Time stepping Interpolations Riemann Solvers • No AMR • Geometry support (Cart, Cyl, Spher) • Serial/Parallel Implementation (MPI)

Requirements • (ANSI) C compiler • Python (v. > 1. 6) • GNU Make Optional • MPI (arraylib by A. Malagoli) • GD graphics library

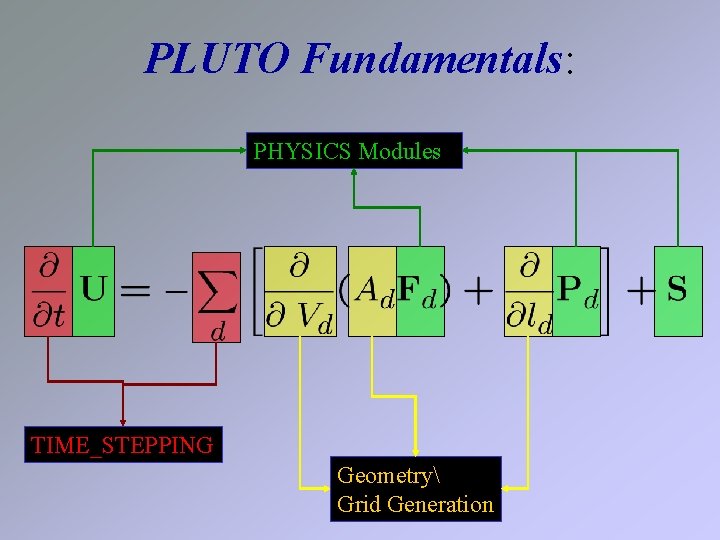
PLUTO Fundamentals: PHYSICS Modules TIME_STEPPING Geometry Grid Generation

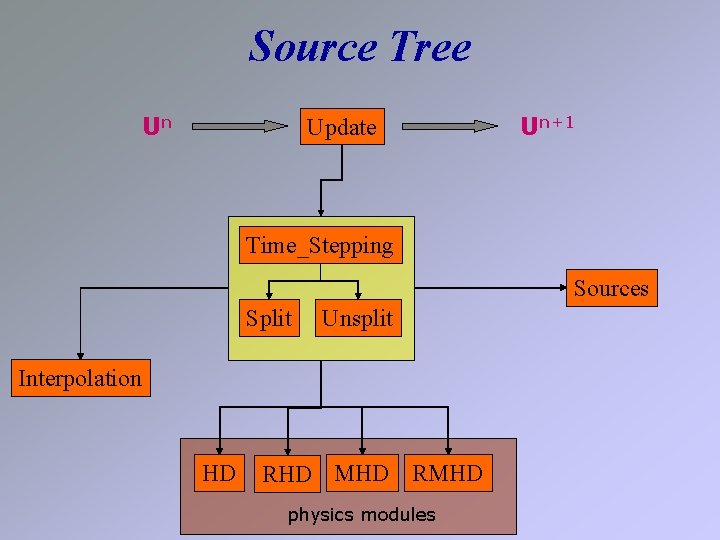
Source Tree Un Update Un+1 Time_Stepping Sources Split Unsplit Interpolation HD RHD MHD RMHD physics modules

Hydrodynamics (HD) Module Eos:

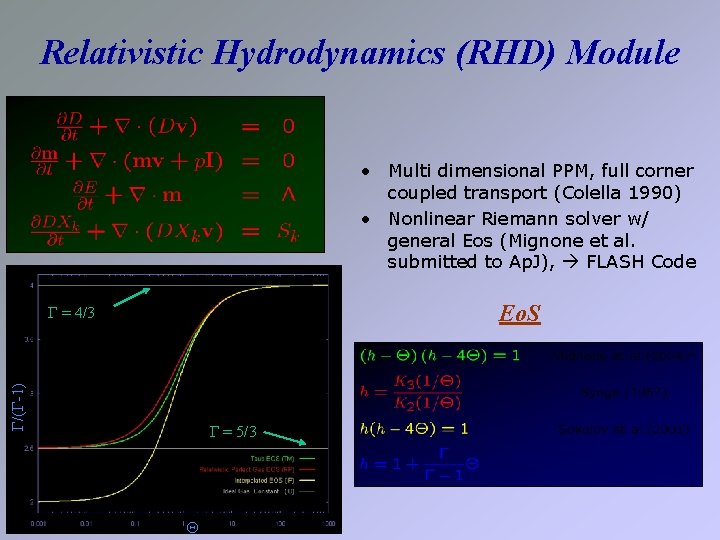
Relativistic Hydrodynamics (RHD) Module • Multi dimensional PPM, full corner coupled transport (Colella 1990) • Nonlinear Riemann solver w/ general Eos (Mignone et al. submitted to Ap. J), FLASH Code Eo. S /( -1) = 4/3 = 5/3

Magnetohydrodynamics (MHD) Module • Monopole Control – Powell (Powell 94) – Monopole Diffusion (Marder 87) – Flux CT (Balsara 2004) • Splitting of Magnetic Field, B = B 0(x) + B 1(x, t) suitable for low- plasma.

Relativistic Magnetohydrodynamics (RMHD) Module • Shares Features w/ MHD and RHD

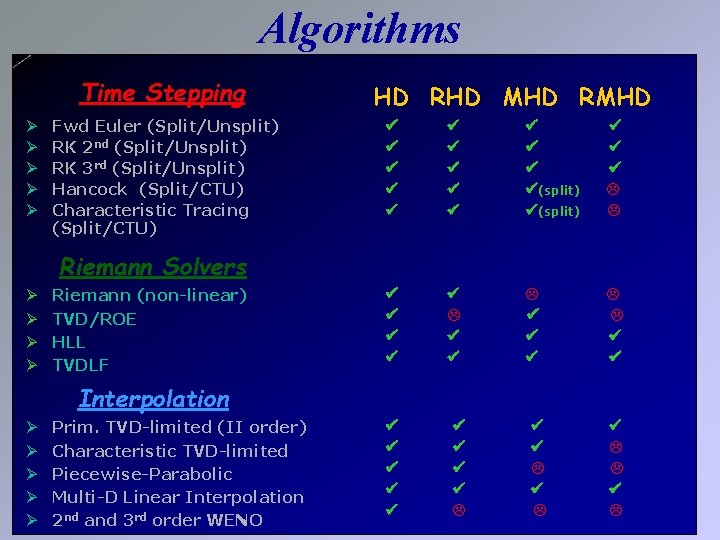
Algorithms Time Stepping Ø Ø Ø Fwd Euler (Split/Unsplit) RK 2 nd (Split/Unsplit) RK 3 rd (Split/Unsplit) Hancock (Split/CTU) Characteristic Tracing (Split/CTU) HD RHD MHD RMHD (split) Riemann Solvers Ø Ø Riemann (non-linear) TVD/ROE HLL TVDLF Interpolation Ø Ø Ø Prim. TVD-limited (II order) Characteristic TVD-limited Piecewise-Parabolic Multi-D Linear Interpolation 2 nd and 3 rd order WENO

Additional Features • Particles (T. Laverne): • Optically thin radiative losses Ø power-law 2 T (Analytic integrator) Ø “Interstellar” cooling function: § T > 104 K, Dalgarno & Mc. Cray Cooling (1972) § T < 104 K, NEQ (H + H 2) (Oliva, 1992) Ø NEQ cooling function for shocks < 80 Km/s (Raymond 1987) • Implicit Thermal Conduction (1 -D only) Explicit /Implicit 2 nd order integrators

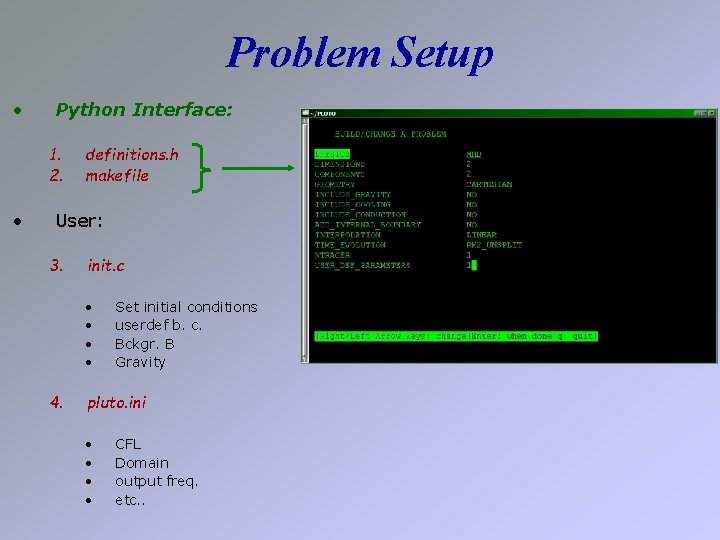
Problem Setup • Python Interface: 1. 2. • definitions. h makefile User: 3. init. c • • 4. Set initial conditions userdef b. c. Bckgr. B Gravity pluto. ini • • CFL Domain output freq. etc. .

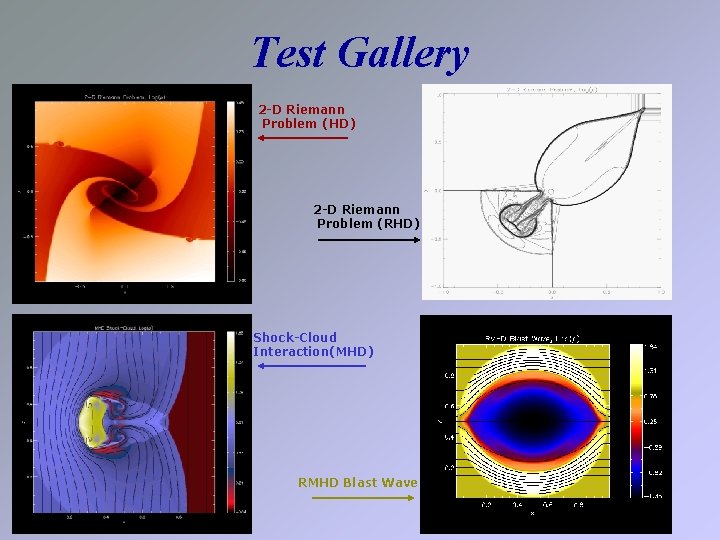
Test Gallery 2 -D Riemann Problem (HD) 2 -D Riemann Problem (RHD) Shock-Cloud Interaction(MHD) RMHD Blast Wave

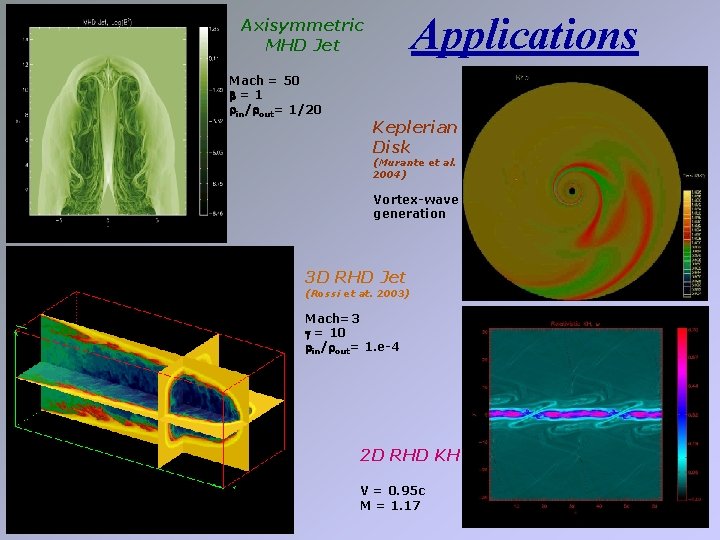
Applications Axisymmetric MHD Jet Mach = 50 =1 in/ out= 1/20 Keplerian Disk (Murante et al. 2004) Vortex-wave generation 3 D RHD Jet (Rossi et at. 2003) Mach=3 = 10 in/ out= 1. e-4 2 D RHD KH V = 0. 95 c M = 1. 17

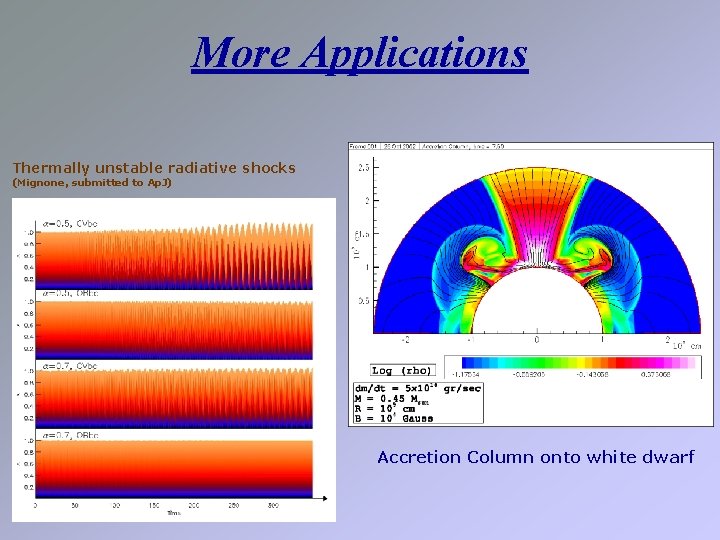
More Applications Thermally unstable radiative shocks (Mignone, submitted to Ap. J) Accretion Column onto white dwarf

Summary • • • Simple, fast code for single/multi proc. User-friendly versatile suitable for algorithm comparison (fairly) well documented >> Official release: Feb 2005 << mignone@oddjob. uchicago. edu, bodo@to. astro. it