PLT 328 ROBOTIC CONTROL CHAPTER 3 NONLINEAR CONTROL

PLT 328 ROBOTIC CONTROL CHAPTER 3: NON-LINEAR CONTROL

Objectives �To understand the importance of nonlinear system in robotic �To investigate the process linearization for nonlinear problem �To stabilize the nonlinear problem by using lyapunov stability

Introduction �Importance of nonlinear system in robotic control : 1. Able to deal with uncertainty parameter, mainly due to lack of knowledge of the system. 2. exhibits characteristics of both continuous-time and discrete-time dynamical systems 3. Useful in designing of complex robot with multiple isolated equilibrium points.

Equilibrium point �equilibrium is stable if all solutions close to it at the initial moment will not depart too far from it later on.

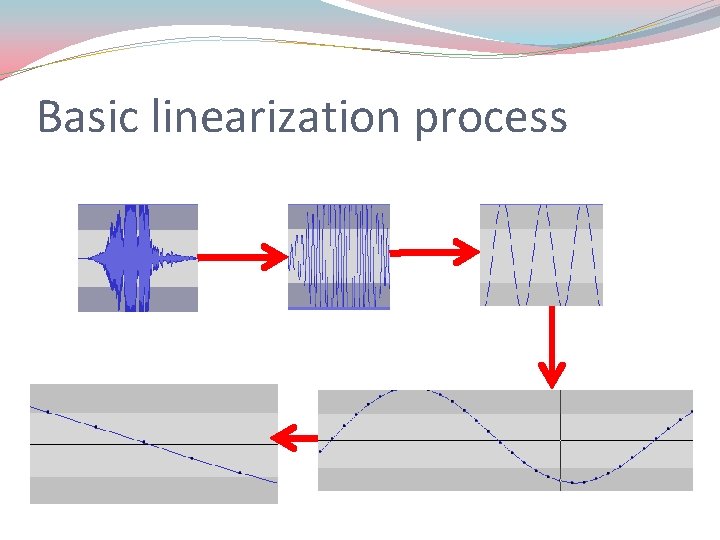
Basic linearization process

Linearization Technique �Consider the autonomous system �and assume that (x 0, y 0) is an equilibrium point. Step 1 �to find the closest linear system when (x, y) is close to (x 0, y 0), the Jacobian matrix is applied

Step 2 �Find the Eigen values of jacobian matrix Step 3 �Determine the stability of system from Eigen values

Step 1: Jacobian matrix

Example �Find the jacobian matrix for the following system when (x 0, y 0) is (2, 1)

Step 2: Eigen values Let x be an eigenvector of the matrix A. Then there must exist an eigenvalue λ such that Ax = λx or, equivalently, Ax - λx = 0 or (A – λI)x = 0 det(A – λI) = 0 This is called the characteristic equation of A. Its roots determine the eigenvalues of A.

Example 1: Find the eigenvalues of two eigenvalues: 1, 2 Note: The roots of the characteristic equation can be repeated. That is, λ 1 = λ 2 =…= λk. If that happens, the eigenvalue is said to be of multiplicity k. Example 2: Find the eigenvalues of λ = 2 is an eigenvector of multiplicity 3.

Example �Find the eigenvalues and eigenvectors of the matrix

�Solution

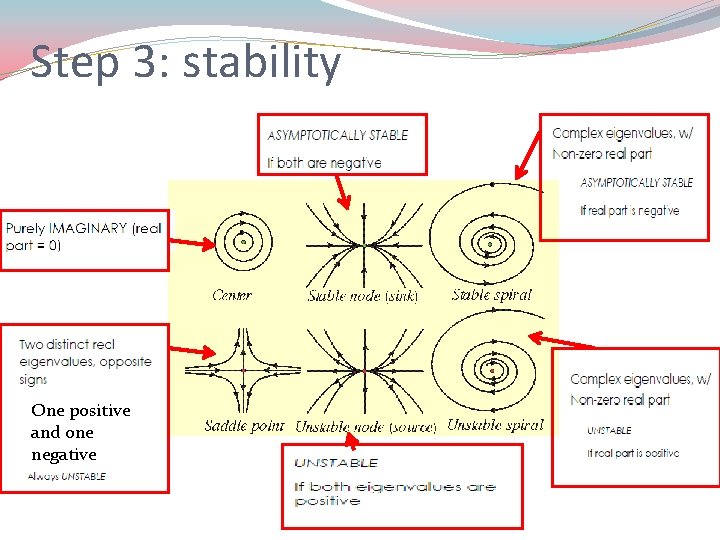
Step 3: stability One positive and one negative

Example �Linearise the system around its equlibrium point of (x, y)=(3, 2).

Final 2018

Lyapunov stability �Lyapunov stability of an equilibrium means that solutions starting "close enough" to the equilibrium �The rate of change of V is given as

Definiteness of Lyapunov Positive definite Unstable Positive semi definite Negative semi definite Stable

Example The equilibrium point for this system is x = 0. Determine the stability of the system by using the Lyapunov function.

Exercise Consider the nonlinear system The candidate lyapunov function is The equilibrium point for this system is x = 1. Determine the stability of the system by using the Lyapunov function.