PLT 121 Chapter 3 Three Phase System INTRODUCTION

PLT 121 Chapter 3 Three Phase System

INTRODUCTION TO THREE PHASE SYSTEM In general, three phase systems are preferred over single phase systems for the transmission of the power system for many reasons, including the following: • Thinner conductors can be used to transmit the same k. VA at the same voltage, which reduces the amount of copper required (typically about 25% less) and turn reduces construction and maintenance costs.

• The lighter lines are easier to install, and the supporting structures can be less massive and farther apart. • In general, most larger motors are three phase because they are essentially self starting and do not require a special design or additional starting circuitry.

Three phase voltages A 3 -phase generator basically consists of a rotating magnet (called the rotor) surrounded by a stationary winding (called the stator). Three separate windings or coils with terminals a-a’, b-b’ and c-c’ are physically placed 120 o apart around the stator.

Generated Voltages The three phase generator can supply power to both single phase and three phase loads

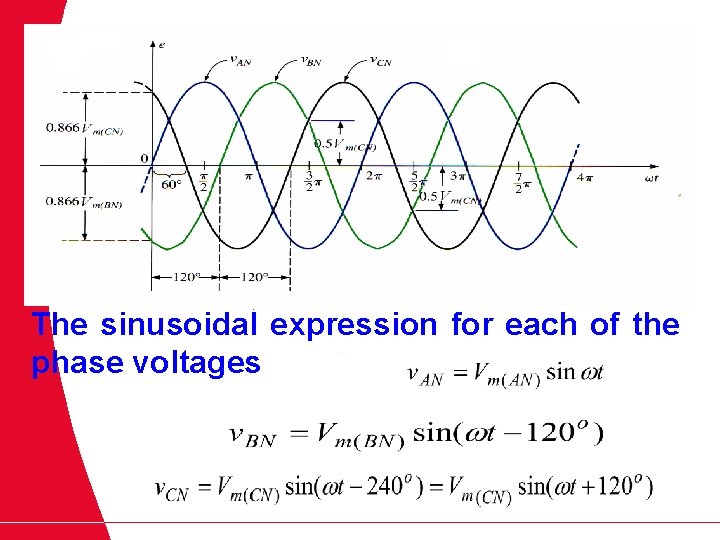
The sinusoidal expression for each of the phase voltages

The phasor diagram of the phase voltages The effective value of each is determined by

If the voltage sources have the same amplitude and frequency ω and are out of the phase with each other by 120 o, the voltages are said to be balanced. By rearranging the phasors as shown in figure below, so Where

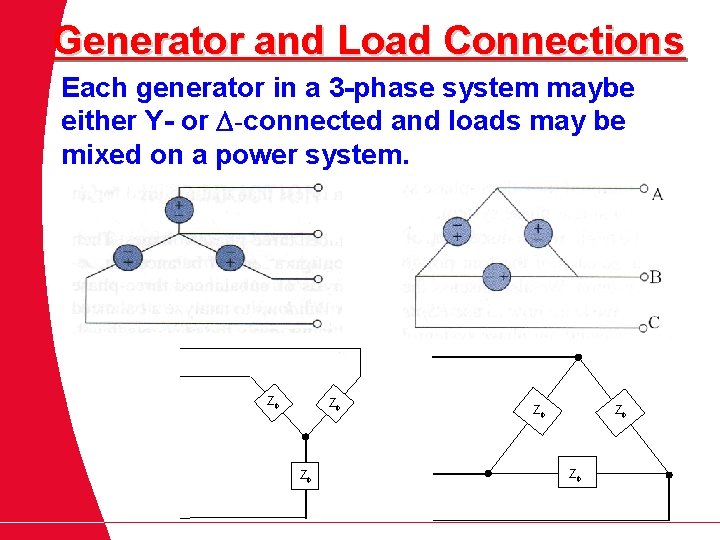
Generator and Load Connections Each generator in a 3 -phase system maybe either Y- or -connected and loads may be mixed on a power system. Z Z Z

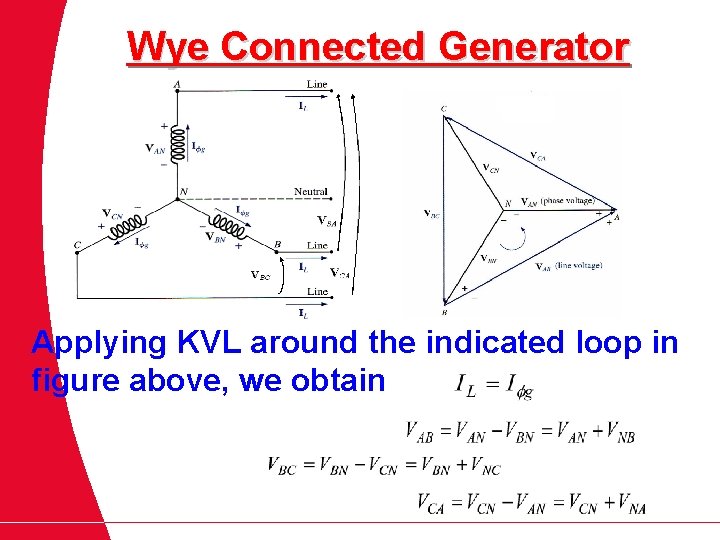
Wye Connected Generator Applying KVL around the indicated loop in figure above, we obtain

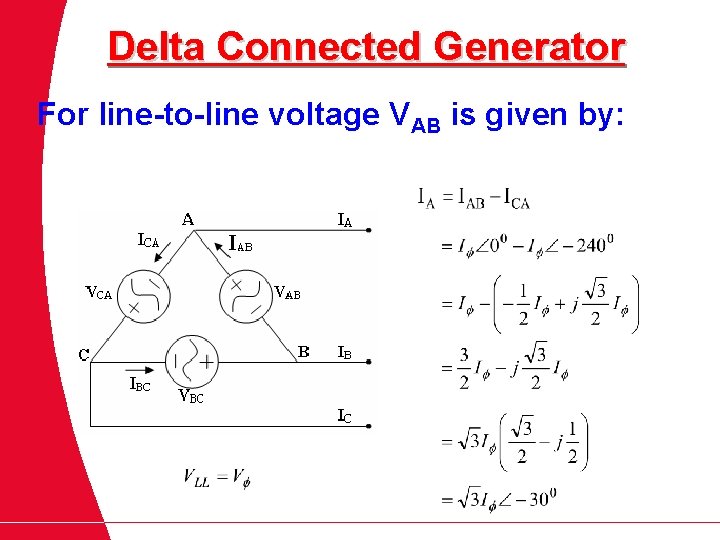
For line-to-line voltage VAB is given by:

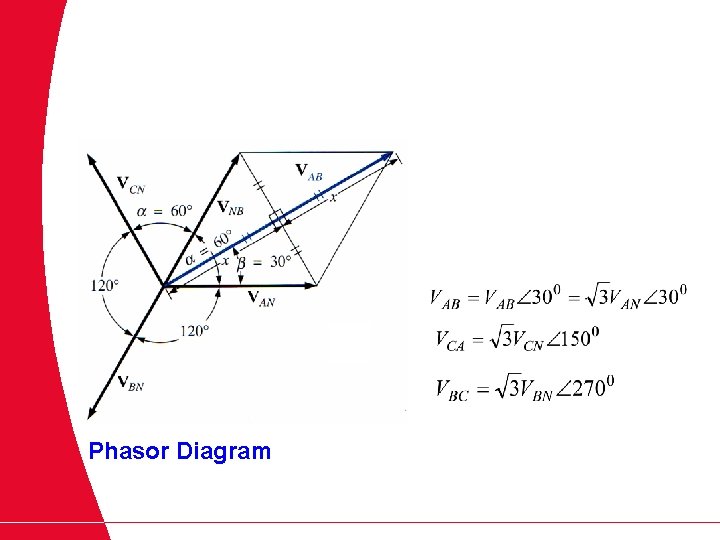
Phasor Diagram

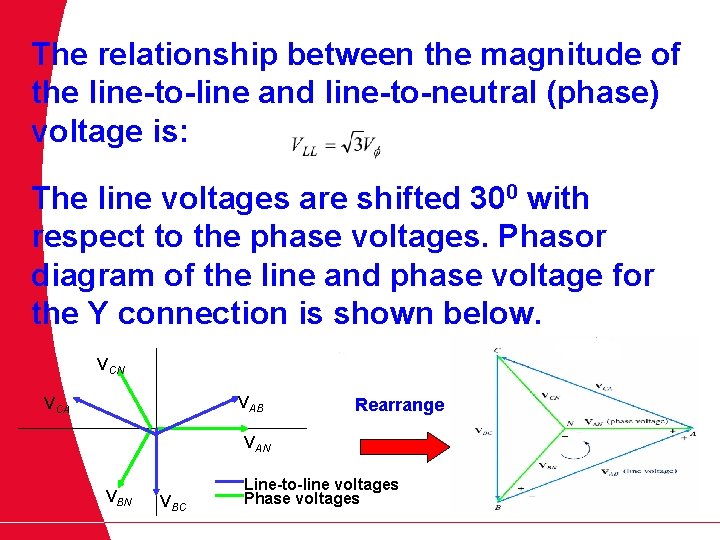
The relationship between the magnitude of the line-to-line and line-to-neutral (phase) voltage is: The line voltages are shifted 300 with respect to the phase voltages. Phasor diagram of the line and phase voltage for the Y connection is shown below. VCN VAB VCA Rearrange VAN VBC Line-to-line voltages Phase voltages

Delta Connected Generator For line-to-line voltage VAB is given by:

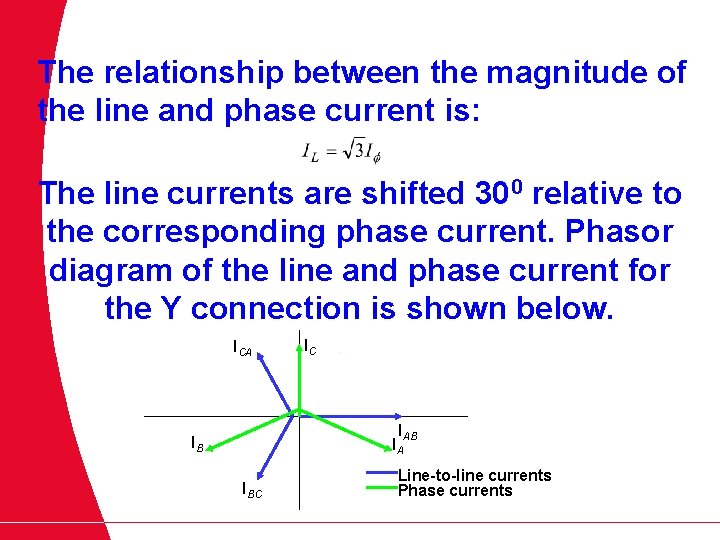
The relationship between the magnitude of the line and phase current is: The line currents are shifted 300 relative to the corresponding phase current. Phasor diagram of the line and phase current for the Y connection is shown below. ICA IC IAB IB IA IBC Line-to-line currents Phase currents

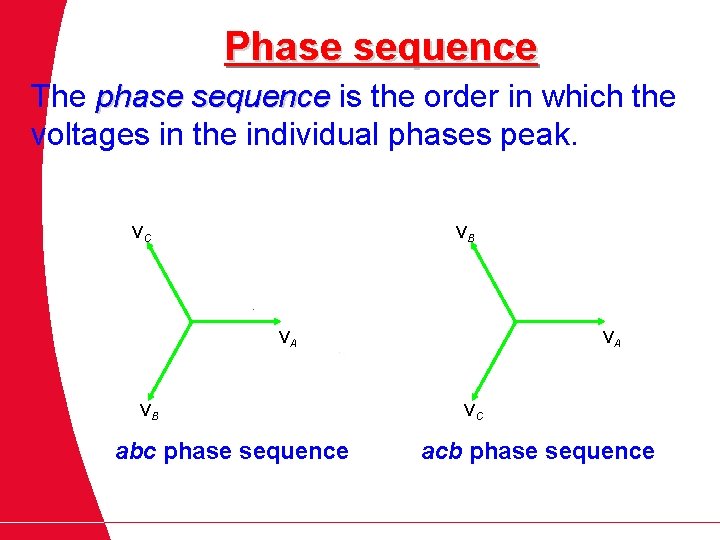
Phase sequence The phase sequence is the order in which the voltages in the individual phases peak. VC VB VA VB abc phase sequence VA VC acb phase sequence

Power relationship - Phase quantities The power equations applied to Y-or load in a balanced 3 -phase system are: Real power Unit=Watts(W) Reactive power Unit=Volt-Amps-Reactive (VAR) Apparent power Unit=Volt-Amps (VA) - angle between voltage and current in any phase of the load

Power relationship - Line quantities The power equations applied to Y-or load in a balanced 3 -phase system are: Real power Reactive power Apparent power - angle between phase voltage and phase current in any phase of the load

Since both the three-phase source and the three-phase load can be either Y- or connected, we have 4 possible connections: i) Y-Y connections (i. e: Y-connected source with a Y-connected load). ii)Y- connection. iii) - connection iv) -Y connection

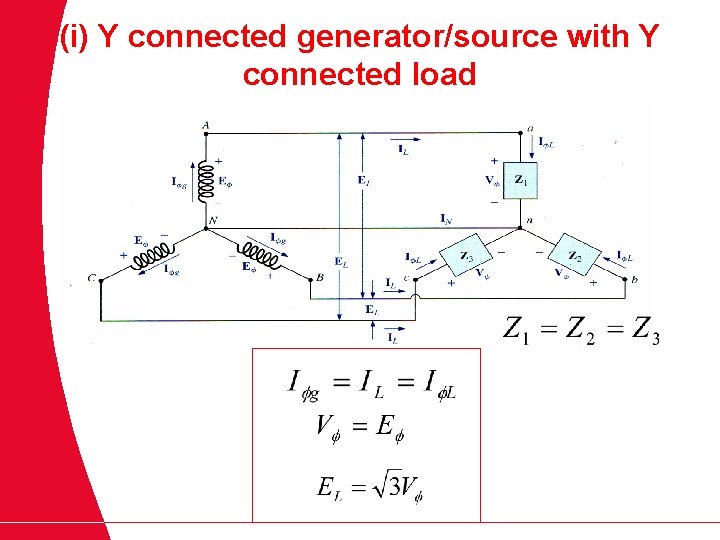
(i) Y connected generator/source with Y connected load

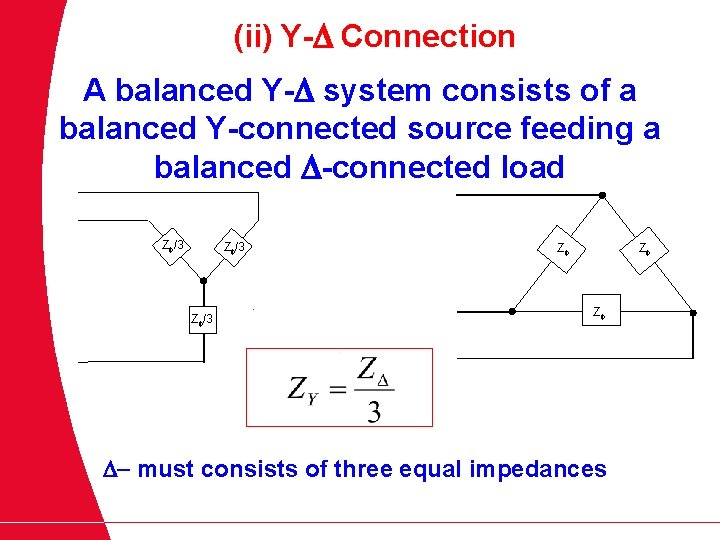
(ii) Y- Connection A balanced Y- system consists of a balanced Y-connected source feeding a balanced -connected load Z /3 Z Z Z - must consists of three equal impedances

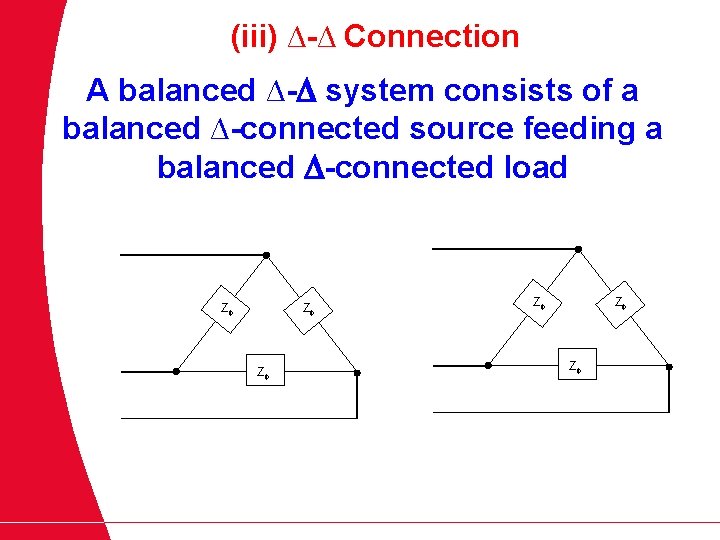
(iii) ∆-∆ Connection A balanced ∆- system consists of a balanced ∆-connected source feeding a balanced -connected load Z Z Z

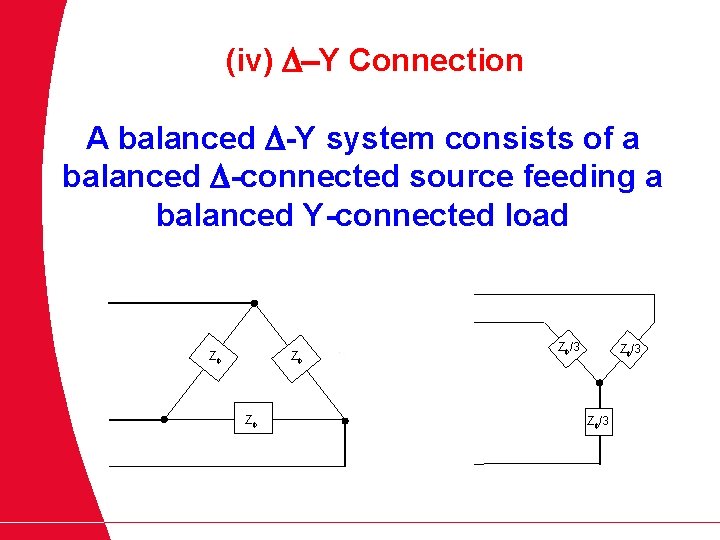
(iv) -Y Connection A balanced -Y system consists of a balanced -connected source feeding a balanced Y-connected load Z Z /3

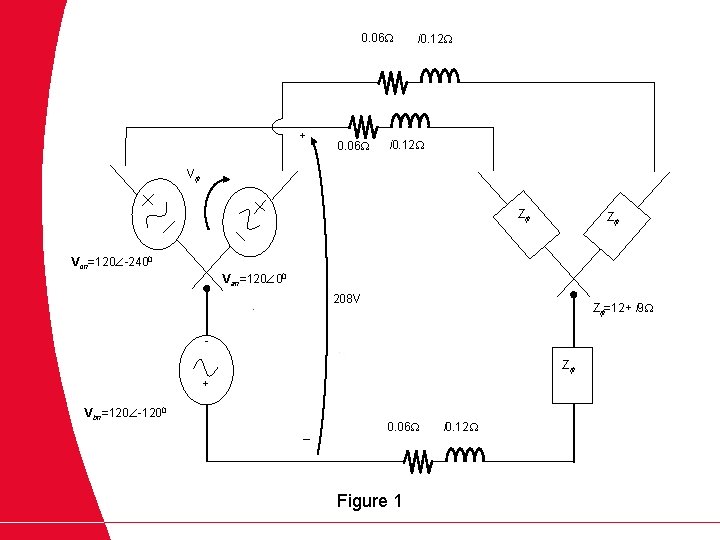
Example 1 A 208 V three-phase power system is shown in Figure 1. It consists of an ideal 208 V Y-connected three-phase generator connected to a three-phase transmission line to a Y-connected load. The transmission line has an impedance of 0. 06+j 0. 12 W per phase, and the load has an impedance of 12+j 9 W per phase. For this simple system, find (a) The magnitude of the line current IL (b) The magnitude of the load’s line and phase voltages VLL and Vf. L (c) The real, reactive and apparent powers consumed by the load (d) The power factor of the load (e) The real, reactive and apparent powers consumed by the transmission line (f) The real, reactive and apparent powers supplied by the generator (g) The generator’s power factor

0. 06 + 0. 06 i 0. 12 V Z Z Vcn=120 -2400 Van=120 00 208 V Z =12+ i 9 Z + Vbn=120 -1200 _ 0. 06 Figure 1 i 0. 12

Solution Example 1 (a)The magnitude of the line current IL So, the magnitude of the line current is thus 7. 94 A

(b) The magnitude of the load’s line and phase voltages VLL and Vf. L The phase voltage on the load is the voltage across one phase of the load. This voltage is the product of the phase impedance and the phase current of the load: Therefore, the magnitude of the load’s phase voltage is and the magnitude of the load’s line voltage is

(c) The real power consumed by the load is The reactive power consumed by the load is The apparent power consumed by the load is

(d) The load power factor is (e) The current in the transmission line is and the impedance of the line is or per phase. Therefore, the real, reactive and apparent powers consumed in the line are:

(f) The real and reactive powers supplied by the generator are the sum of the powers consumed by the line and the load: The apparent power of the generator is the square root of the sum of the squares of the real and reactive powers:

(g) From the power triangle, the power factor angle is Therefore, the generator’s power factor is

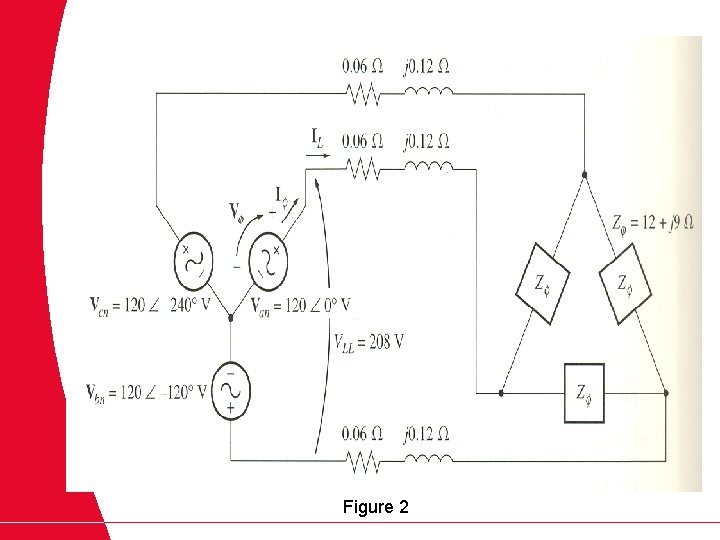
Assignment 2 A 208 V three-phase power system is shown in Figure 2. It consists of an ideal 208 V Y-connected three-phase generator connected to a three -phase transmission line to a -connected load. The transmission line has an impedance of 0. 06+j 0. 12 W per phase, and the load has an impedance of 12+j 9 W per phase. For this simple system, find (a) The magnitude of the line current IL (b) The magnitude of the load’s line and phase voltages VLL and V f. L (c) The real, reactive and apparent powers consumed by the load (d) The power factor of the load (e) The real, reactive and apparent powers consumed by the transmission line (f) The real, reactive and apparent powers supplied by the generator (g) The generator’s power factor

Figure 2