Plotting complex numbers on the complex plane Lesson

Plotting complex numbers on the complex plane

Lesson Objective: Upon the completion of this lesson, you should be able to -plot complex numbers on complex plane. - Convert polar form of complex numbers to their rectangular form and vice versa. - Apply De Moivre’s theorem to compute powers of complex numbers.
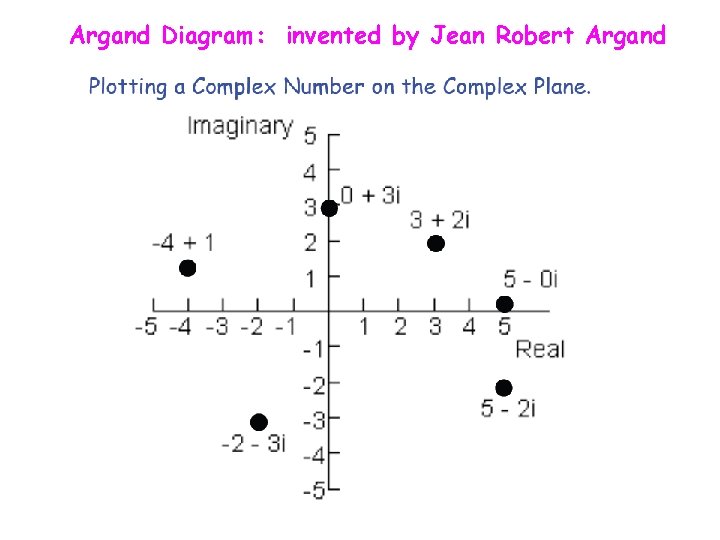
Argand Diagram: invented by Jean Robert Argand

Modulus of a complex number A complex number can be represented by the position vector. Im y The Modulus of a complex number is the distance from the origin to the point. x Re

Example Find a) |3 + 4 i| = 5 b) |5 – 12 i| = 13
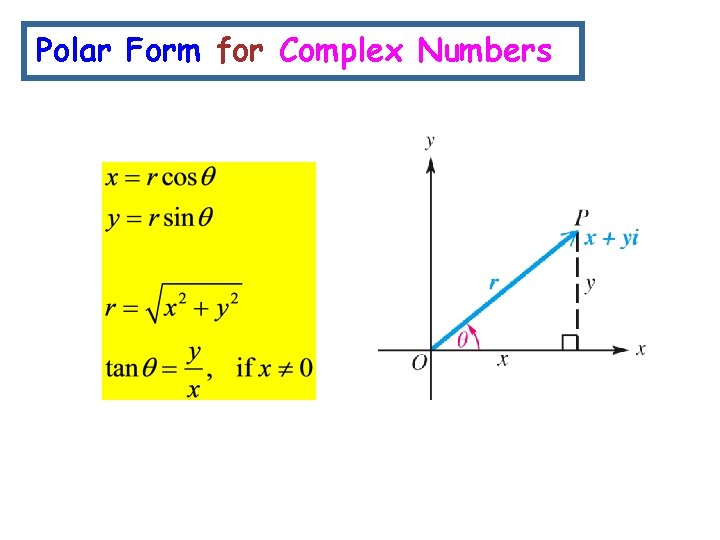
Polar Form for Complex Numbers

Polar Form of a Complex Number The expression is called the polar form of the complex number x + yi. * r is called the modulus and is known as the argument The expression cos + i sin is sometimes abbreviated cis .

Example-1: Convert the following into their rectangular (cartesian) form. a) 4 (cos 300+isin 300) b) 2 Cis 1200

Example-2: Rewrite the following complex numbers in their polar form. a) b) 4 i

De Moivre’s Theorem -French Mathematician -A friend of Isaac Newton

Abraham De Moivre is also famed for predicting the day of his own death. He noted that each night he was sleeping 15 minutes longer and by treating this an arithmetic progression and summing it, he calculated that he would die on the day that he slept for 24 hours. This was 27 November 1754 and he was right!

Let’s discover his findings: Aim: To simplify
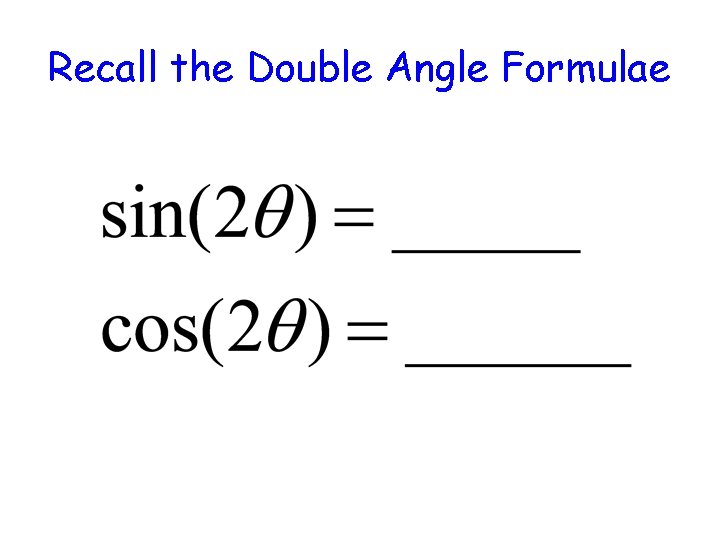
Recall the Double Angle Formulae
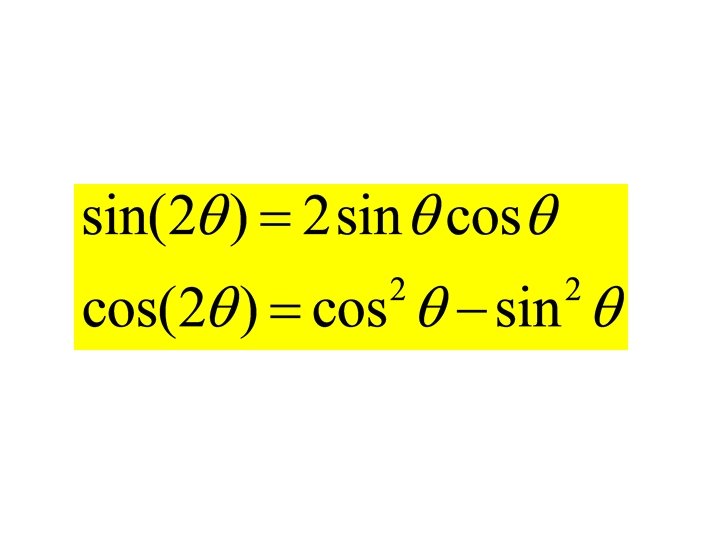
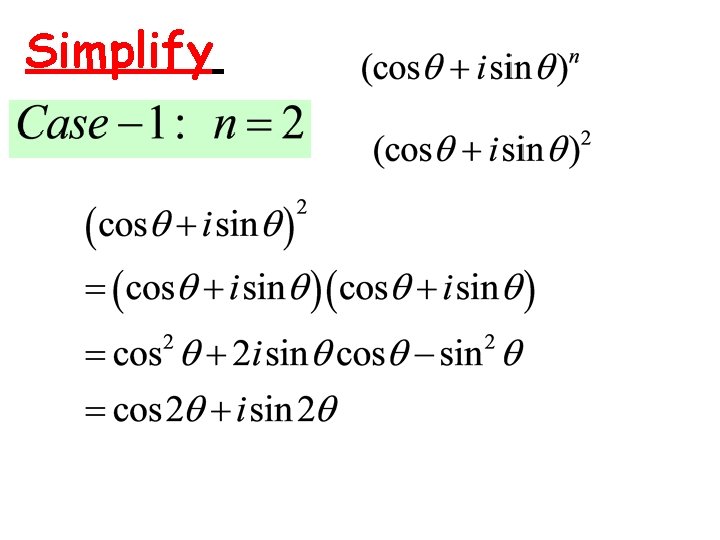
Simplify



Continuing this process, when n is a positive integer,

Case -4 : if n is a negative integer Let n=-m where m is positive integer
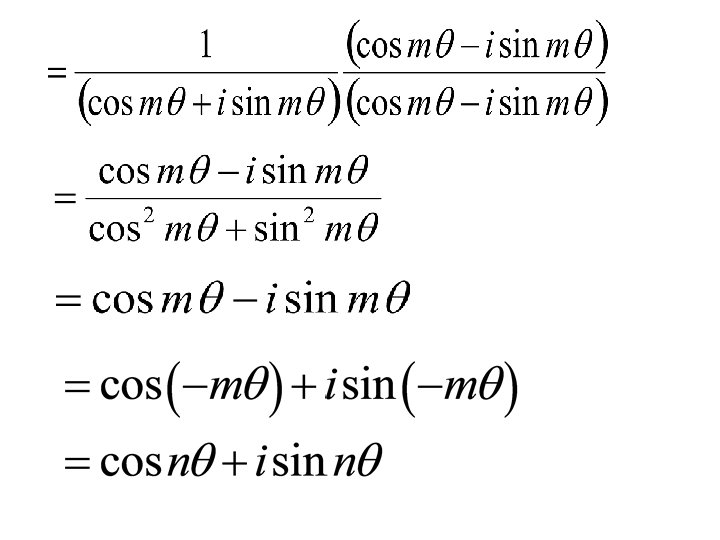

De Moivre’s theorem For all integers n, is
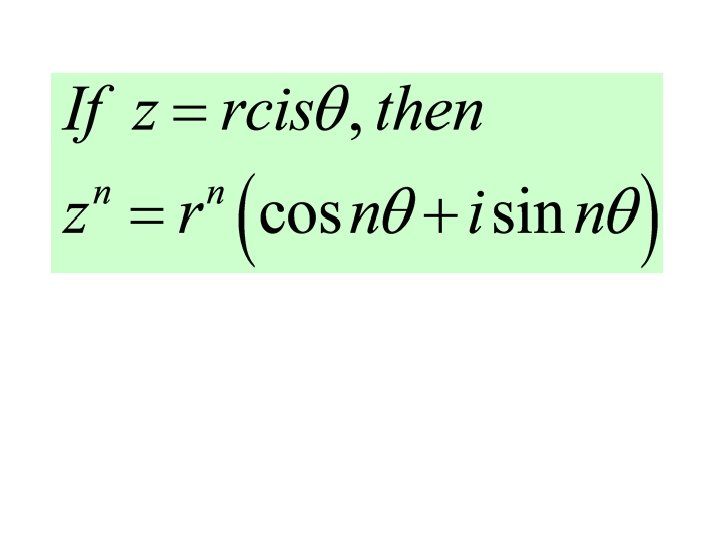

Ex A Let z = 1 − i. m p L E : Find

Pair-work Worksheet

Homework Page-535 7, 11, 14, 15, 17, 19, 21, 23, 36, 37

Classwork Rewrite the following in the form of a+bi:
- Slides: 27