Playing Game with Algorithms Algorithmic Combinatorial Game Theory

Playing Game with Algorithms: Algorithmic Combinatorial Game Theory OUTLINE 1. Introduction 2. Combinatorial Game Theory 3. Algorithms for Two-Player Games 4. Algorithms for Puzzles

Introduction o One-player puuzzles Often NP-complete Ex: Minesweeper (踩地雷) o Two-player gaems Often PSPACE-complete Othello (黑白棋) or EXPTIME-complete Chess , Go o 對人類而言的難易度. . 對電腦而言並不一定 完全相等

PSPACE-complete o o PSPACE: The set of decision problems that can be solved by a Turing machine using a polynomial amount of memory, and unlimited time. PSPACE-complete: if it is in PSPACE , and every problem in PSPACE can be reduced to it in polynomial time. The problems in PSPACEcomplete can be thought of as the hardest problems in PSPACE

EXPTIME-complete o o EXPSPACE: The set of all decision problems solvable by a deterministic Turing machine in O (2 p(n)) time, where p(n) is a polynomial function of n EXPTIME-complete is also a set of decision problems. A decision problem is in EXPTIMEcomplete if it is in EXPTIME, and every problem in EXPTIME has a polynomial-time many-one reduction to it. . EXPTIME-complete might be thought of as the hardest problems in EXPTIME.

Combinatorial Game Theory o o o Combinatorial Game Theory is typically involves two players, called Left and Right. Left wins; Right wins; first wins; second wins. Two player games can be described by a rooted tree

Conway’s Surreal Numbers o {L|R} n n o Game: {L|R} n n o L <= R Ex: {|}=0; {0|}=1 No constraints L and R All games equal to 0 is second player to move win Other outcome?

Sprague- Grundy Theory Nim is a game played with several heaps. o Nim game with a single heap of size n (*n) called nimber o K piles of sizes n 1, n 2, n 3, …. nk 1 pile of size n XOR (n 1, n 2, n 3, . . nk) <==> n o

Every impartial two-player perfectinformation game has the same calue as a single-pile Nim game, *n. n called G-value, ……. etc o Strategy Stealing n Using contradiction

Algorithms for Two-Player Games o Many nonloopy two-player games are PSPACE-complete and also EXPTIMEcomplete

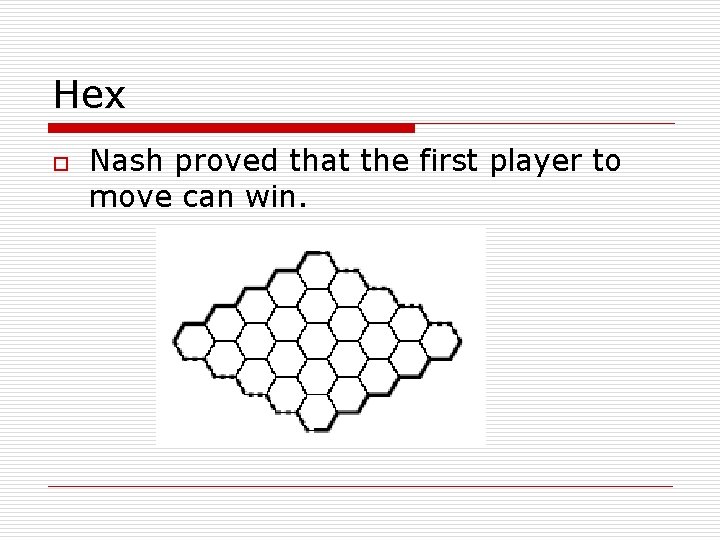
Hex o Nash proved that the first player to move can win.

Checkers o o o 子僅能向斜前方前進，或是跳過對方的子並 取走該子 PSPACE-HARD And EXPTIME-complete