Platonische Krper Polyeder Die 5 platonischen Krper inspirieren

Platonische Körper

Polyeder Die 5 platonischen Körper inspirieren sowohl Wissenschaftler wie auch Mystiker seit Jahrtausenden. Aber wieso gibt es eigentlich nur 5 regelmässige Polyeder? Nach dieser Lektion haben Sie den Beweis in der Tasche!

Inhalt des Vortrags 1. 2. 3. 4. 5. Platonische Körper in der Philosophie Platonische Körper in der Natur Platonische Körper in der Chemie Begriffsklärung Beweis, dass es nur 5 Platonische Körper geben kann

Platonische Körper in • Philosophie • Natur • Chemie

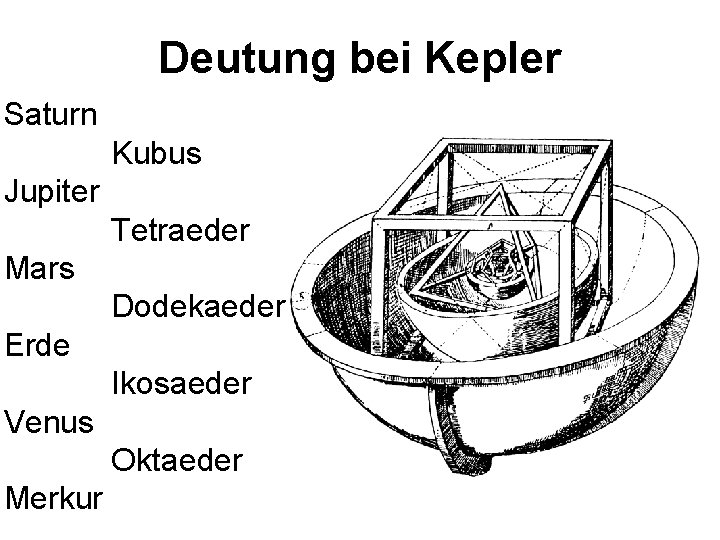
In Platons Timaios-Dialog Platon setzt die 5 regelmässigen Körper in Beziehung zu den Begriffen Erde, Wasser, Luft und Feuer und zum Weltganzen. Diese Darstellung stammt aus dem Buch „Mysterium cosmographicum“ des Astronomen Johannes Kepler.

Deutung bei Kepler Saturn Kubus Jupiter Tetraeder Mars Dodekaeder Erde Ikosaeder Venus Oktaeder Merkur

Kristalle Fluorit Salz Pyrit

Coccosphäre der Alge Braarudosphaera bigelowi

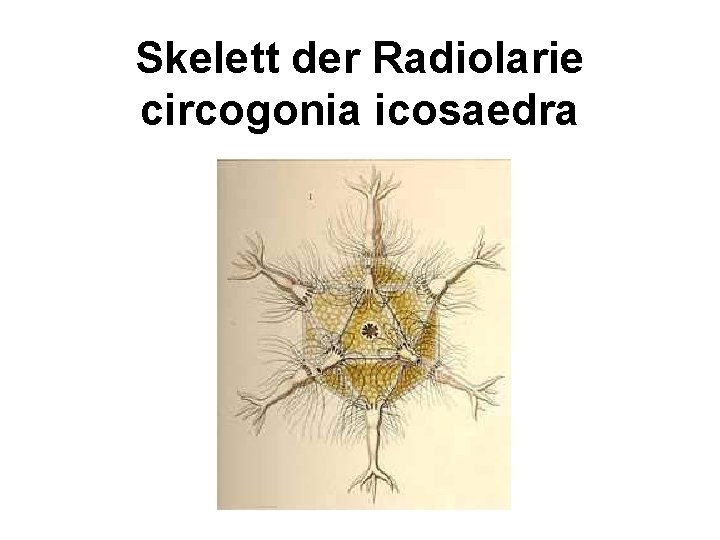
Skelett der Radiolarie circogonia icosaedra

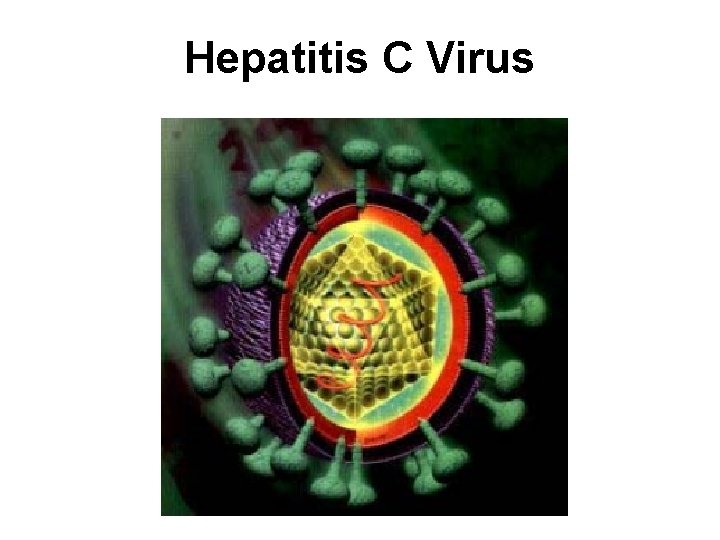
Hepatitis C Virus

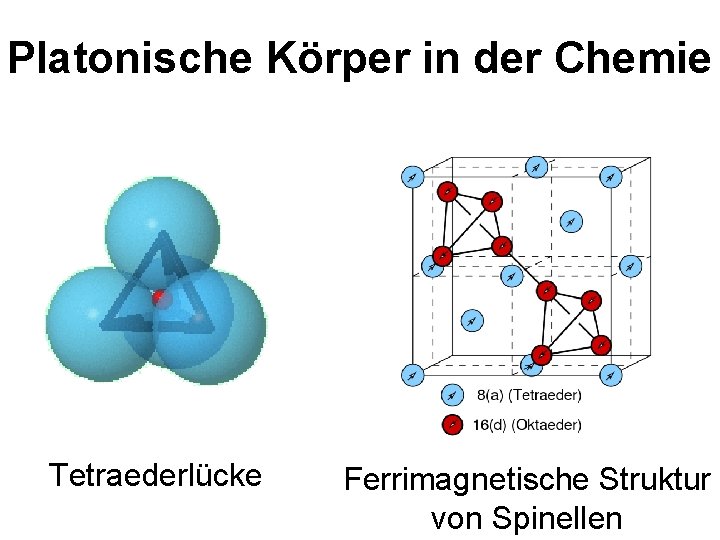
Platonische Körper in der Chemie Tetraederlücke Ferrimagnetische Struktur von Spinellen

Begriffsklärung • • Polyeder Einfache Polyeder Konvexe Polyeder Platonische Polyeder

Polyeder-Begriff Ein Polyeder (Vielflächner) ist ein Teil des dreidimensionalen Raumes, der von Polygonen (Vielecken) begrenzt wird.

Polyeder-Begriff Polyeder können Löcher und innere Hohlräume haben, die dann ebenfalls von geraden Flächen und Kanten begrenzt sein müssen. Sie müssen keinerlei Symmetrie aufweisen.

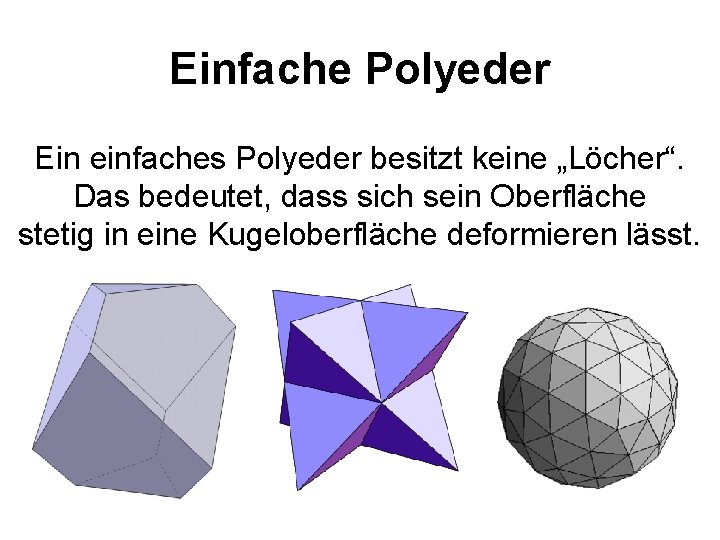
Einfache Polyeder Ein einfaches Polyeder besitzt keine „Löcher“. Das bedeutet, dass sich sein Oberfläche stetig in eine Kugeloberfläche deformieren lässt.

Konvexe Polyeder Ein Polyeder ist konvex, wenn zu je zwei Punkten aus dem Inneren des Polyeders die Verbindungsstrecke zwischen diesen im Innern des Polyeders verläuft.

Nicht-konvexe Polyeder

Definition der Platonischen Körper 1. Platonische Körper sind konvex. 2. Alle Flächen sind regelmässige Vielecke. 3. Alle Flächen sind kongruent. 4. An jeder Ecke stossen gleich viele Kanten zusammen.

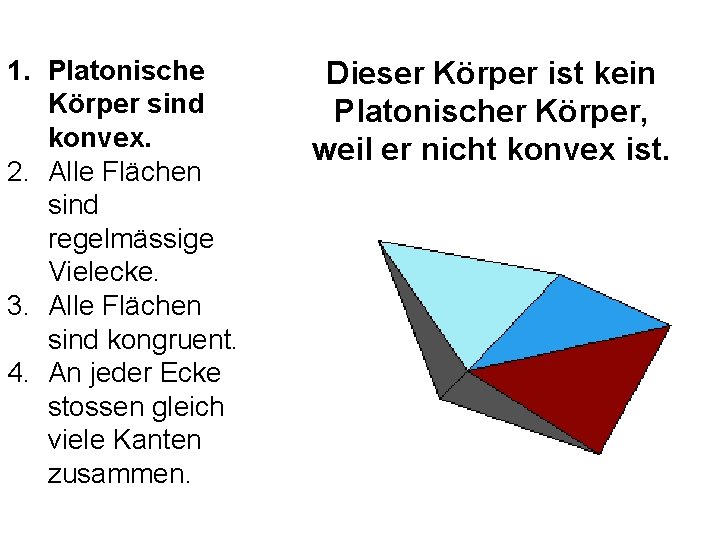
1. Platonische Körper sind konvex. 2. Alle Flächen sind regelmässige Vielecke. 3. Alle Flächen sind kongruent. 4. An jeder Ecke stossen gleich viele Kanten zusammen. Dieser Körper ist kein Platonischer Körper, weil er nicht konvex ist.

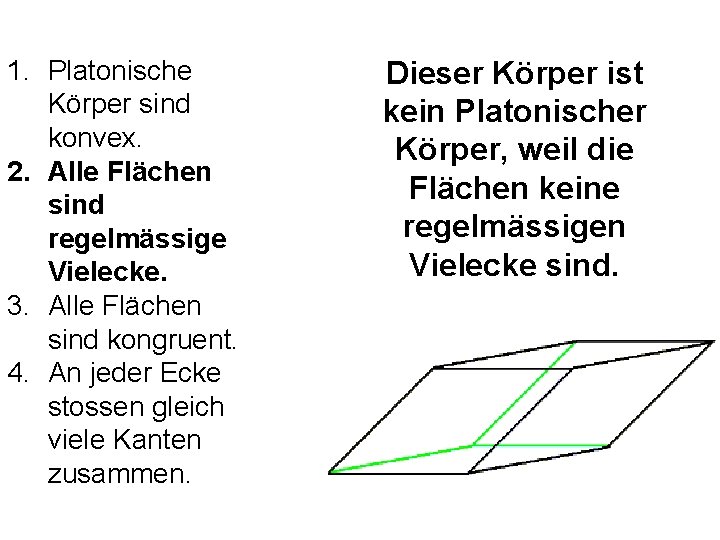
1. Platonische Körper sind konvex. 2. Alle Flächen sind regelmässige Vielecke. 3. Alle Flächen sind kongruent. 4. An jeder Ecke stossen gleich viele Kanten zusammen. Dieser Körper ist kein Platonischer Körper, weil die Flächen keine regelmässigen Vielecke sind.

1. Platonische Körper sind konvex. 2. Alle Flächen sind regelmässige Vielecke. 3. Alle Flächen sind kongruent. 4. An jeder Ecke stossen gleich viele Kanten zusammen. Dieser Körper ist kein Platonischer Körper, weil verschiedenartige Flächen vorkommen.

1. Platonische Körper sind konvex. 2. Alle Flächen sind regelmässige Vielecke. 3. Alle Flächen sind kongruent. 4. An jeder Ecke stossen gleich viele Kanten zusammen. Dieser Körper ist kein Platonischer Körper, weil nicht an jeder Ecke gleich viele Kanten zusammenstossen.

Zusammenfassung der Definition der Platonischen Körper • einfach • konvex • lauter kongruente regelmässige Vielecke • lauter kongruente Ecken

Beweis • • Euklid Polygone Eck-Konfigurationen Konstruktionen

Euklid von Alexandria (ca. 340–ca. 270) Euklid schreibt im 13. Buch seiner Elemente: „Weiter behaupte ich, dass sich ausser den fünf Körpern kein weiterer Körper errichten lässt, der von einander gleichen gleichseitigen und gleichwinkligen Figuren umfasst würde. “

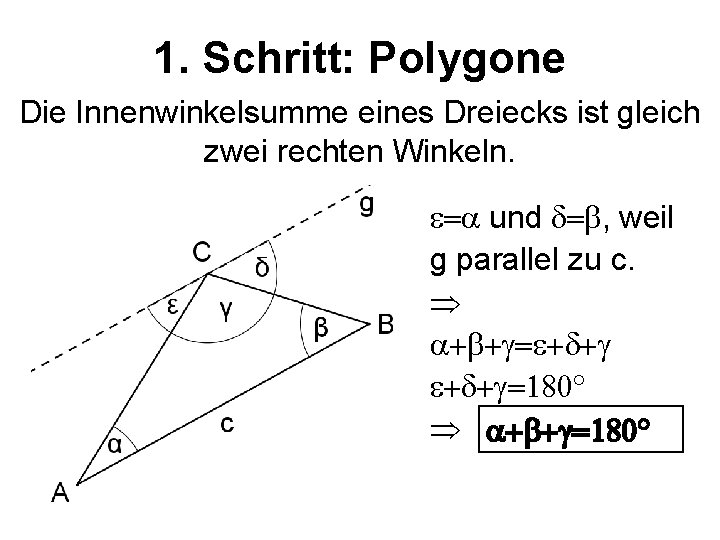
1. Schritt: Polygone Die Innenwinkelsumme eines Dreiecks ist gleich zwei rechten Winkeln. e=a und d=b, weil g parallel zu c. a+b+g=e+d+g=180° a+b+g=180°

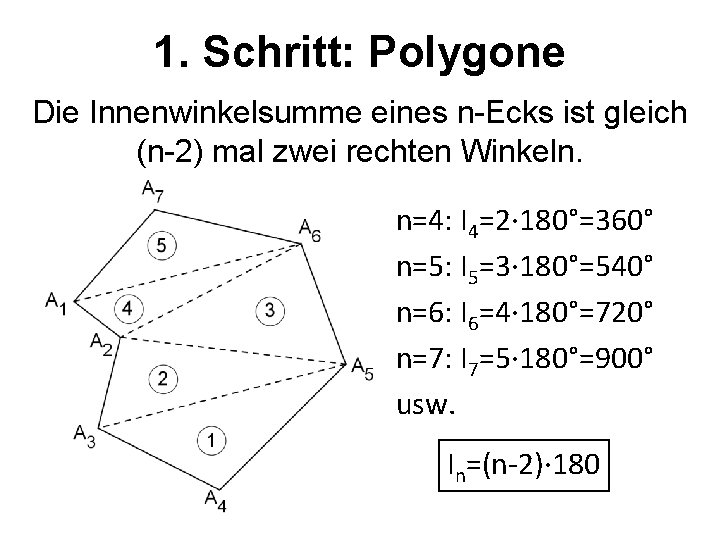
1. Schritt: Polygone Die Innenwinkelsumme eines n-Ecks ist gleich (n-2) mal zwei rechten Winkeln. n=4: I 4=2∙ 180°=360° n=5: I 5=3∙ 180°=540° n=6: I 6=4∙ 180°=720° n=7: I 7=5∙ 180°=900° usw. In=(n-2)∙ 180

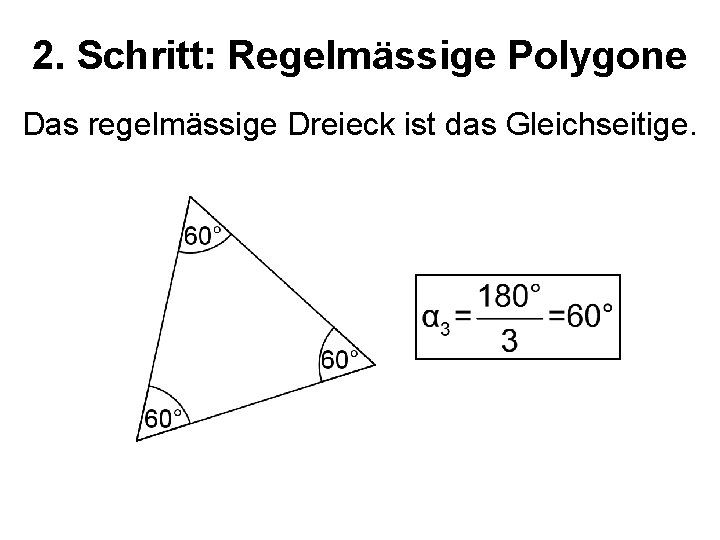
2. Schritt: Regelmässige Polygone Das regelmässige Dreieck ist das Gleichseitige.

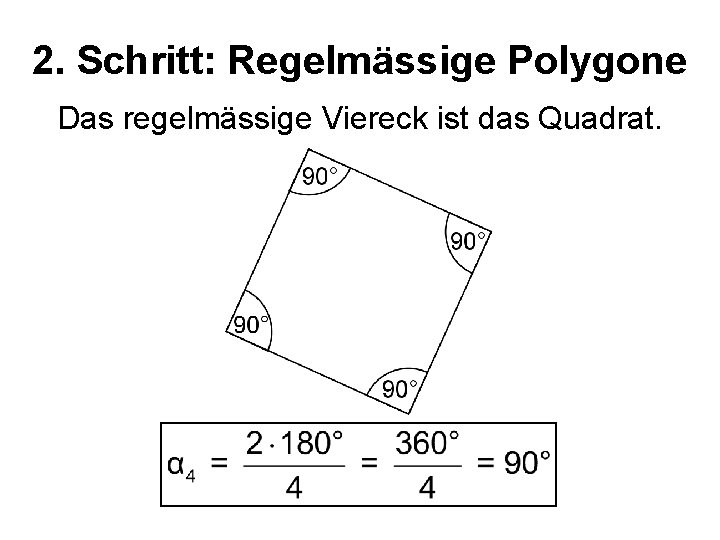
2. Schritt: Regelmässige Polygone Das regelmässige Viereck ist das Quadrat.

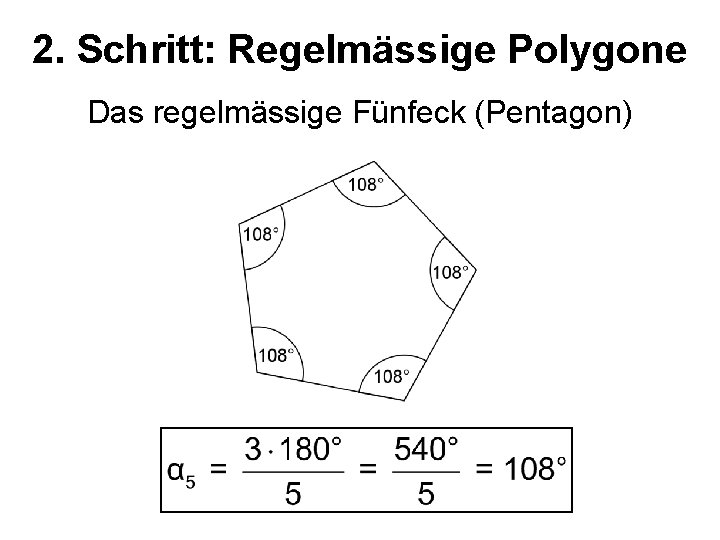
2. Schritt: Regelmässige Polygone Das regelmässige Fünfeck (Pentagon)

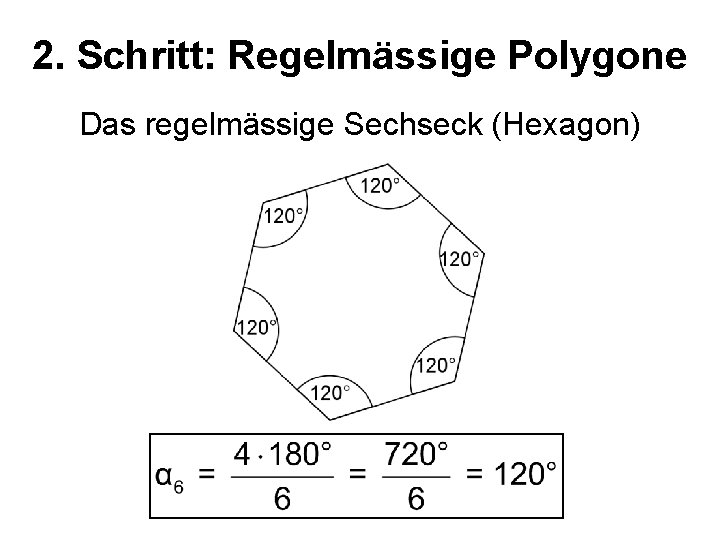
2. Schritt: Regelmässige Polygone Das regelmässige Sechseck (Hexagon)

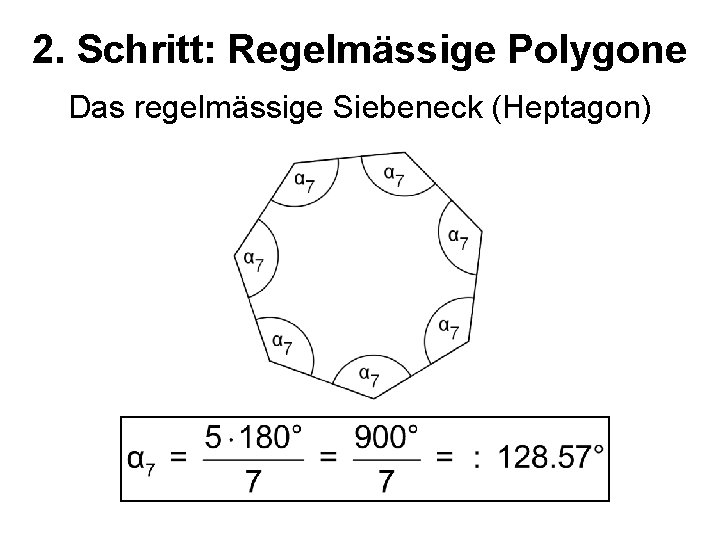
2. Schritt: Regelmässige Polygone Das regelmässige Siebeneck (Heptagon)

2. Schritt: Regelmässige Polygone Übersicht über die Peripheriewinkel n 3 4 5 6 7 8 9 10 →� 60° 90° 108° 120° 128. 57° 135° 140° 144° 180°

3. Schritt: Bedingung 1. An einer Ecke müssen mindestens drei gleiche Flächen zusammenstossen. 2. Die Summe der Peripheriewinkel der Flächen, die an einer Ecke zusammenstossen, muss kleiner als 360° sein, da sonst die Flächen keine Ecke bilden.

3. Schritt: Gleichseitige Dreiecke An einer Ecke können 3, 4 oder 5 gleichseitige Dreiecke anstossen, nicht aber 6 oder mehr. 3 Dreiecke 3∙ 60°<360° 4 Dreiecke 4∙ 60°<360° 5 Dreiecke 5∙ 60°<360° 6 Dreiecke 6∙ 60°=360° 7 Dreiecke 7∙ 60°>360° usw. – unmöglich!

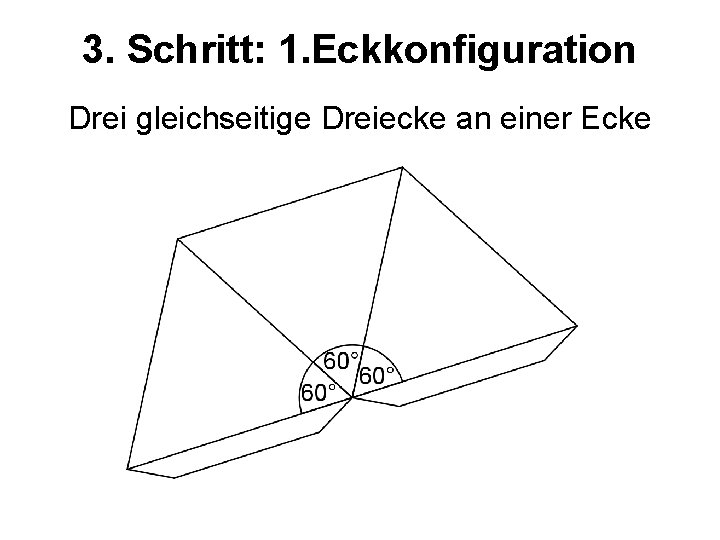
3. Schritt: 1. Eckkonfiguration Drei gleichseitige Dreiecke an einer Ecke

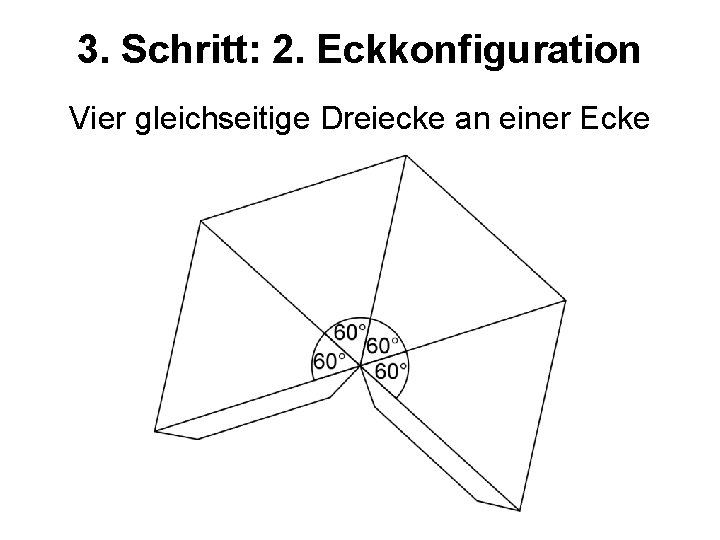
3. Schritt: 2. Eckkonfiguration Vier gleichseitige Dreiecke an einer Ecke

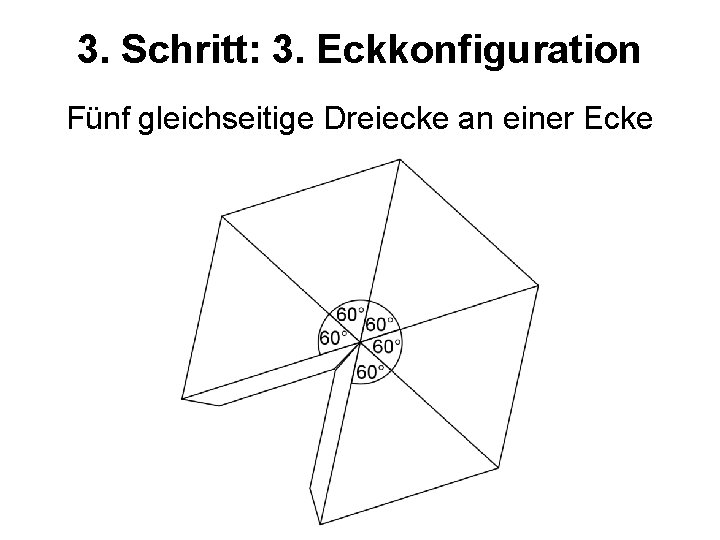
3. Schritt: 3. Eckkonfiguration Fünf gleichseitige Dreiecke an einer Ecke

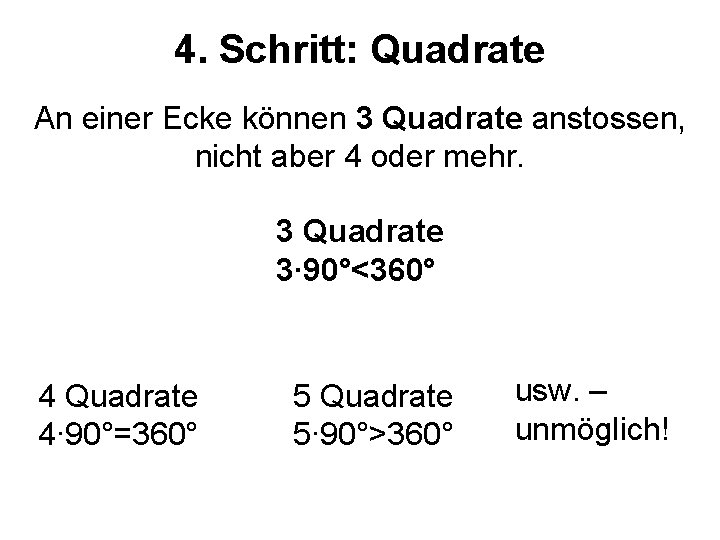
4. Schritt: Quadrate An einer Ecke können 3 Quadrate anstossen, nicht aber 4 oder mehr. 3 Quadrate 3∙ 90°<360° 4 Quadrate 4∙ 90°=360° 5 Quadrate 5∙ 90°>360° usw. – unmöglich!

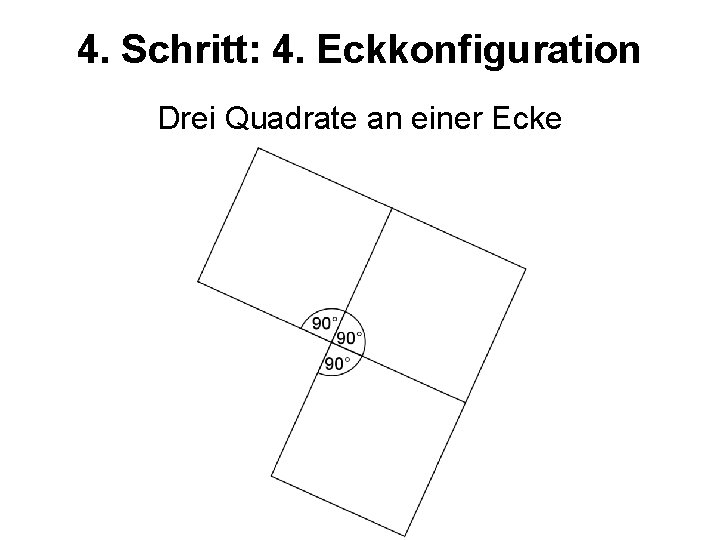
4. Schritt: 4. Eckkonfiguration Drei Quadrate an einer Ecke

5. Schritt: Regelmässige Pentagone An einer Ecke können 3 regelmässige Pentagone anstossen, nicht aber 4 oder mehr. 3 Pentagone 3∙ 108° < 360° 4 Pentagone 5 Pentagone 4∙ 108° > 360° 5∙ 108° > 360° usw. – unmöglich!

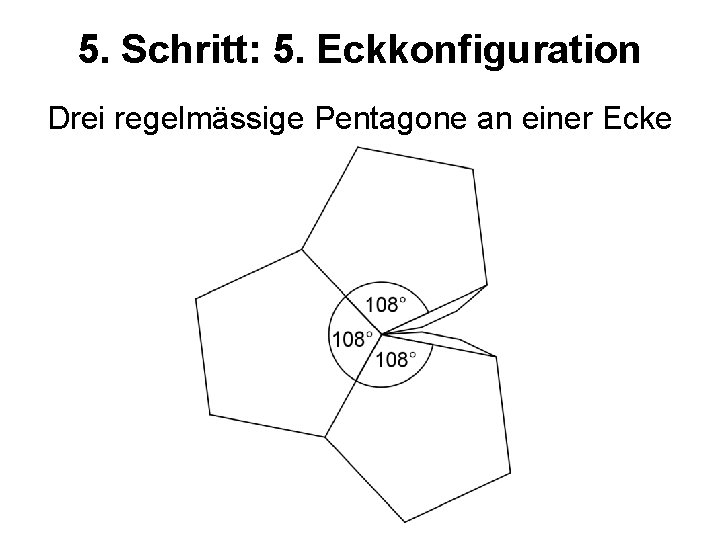
5. Schritt: 5. Eckkonfiguration Drei regelmässige Pentagone an einer Ecke

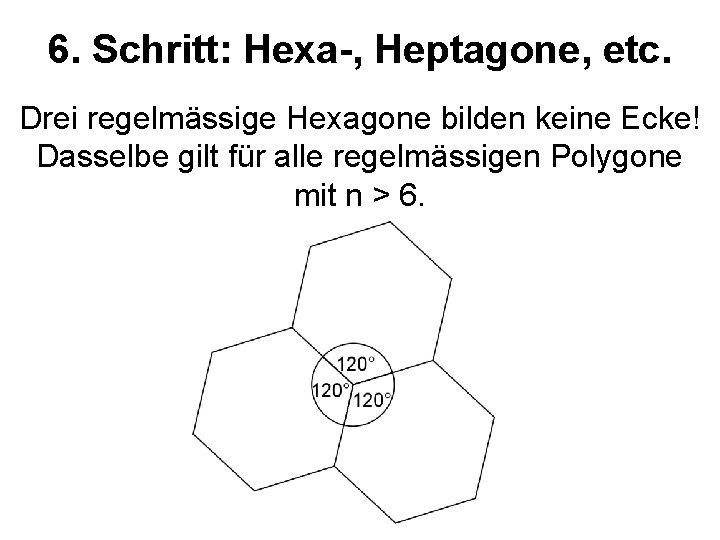
6. Schritt: Hexa-, Heptagone, etc. Drei regelmässige Hexagone bilden keine Ecke! Dasselbe gilt für alle regelmässigen Polygone mit n > 6.

7. Schritt: Konstruktion Es kann also nur gerade 5 reguläre, konvexe Polyeder geben, bei denen an jeder Ecke gleich viele reguläre Polygone anstossen. Ende des Beweises hx/wzbw/qed Die 5 Platonischen Körper ergeben sich durch Konstruktion aus den 5 erlaubten Eckkonfigurationen:

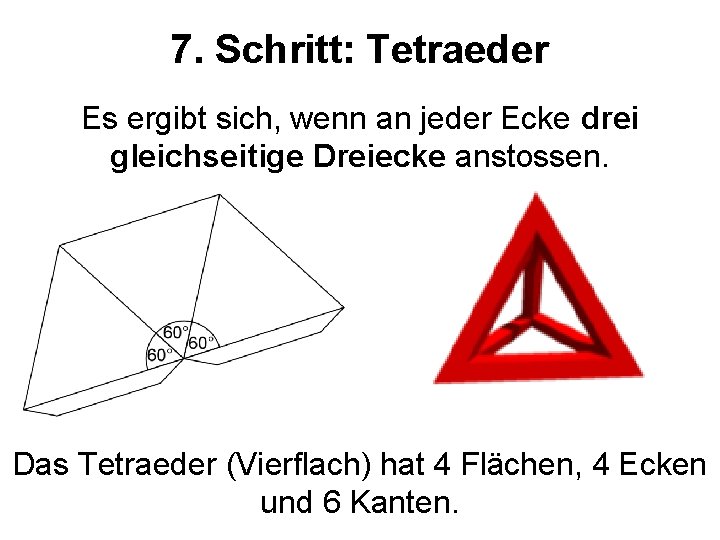
7. Schritt: Tetraeder Es ergibt sich, wenn an jeder Ecke drei gleichseitige Dreiecke anstossen. Das Tetraeder (Vierflach) hat 4 Flächen, 4 Ecken und 6 Kanten.

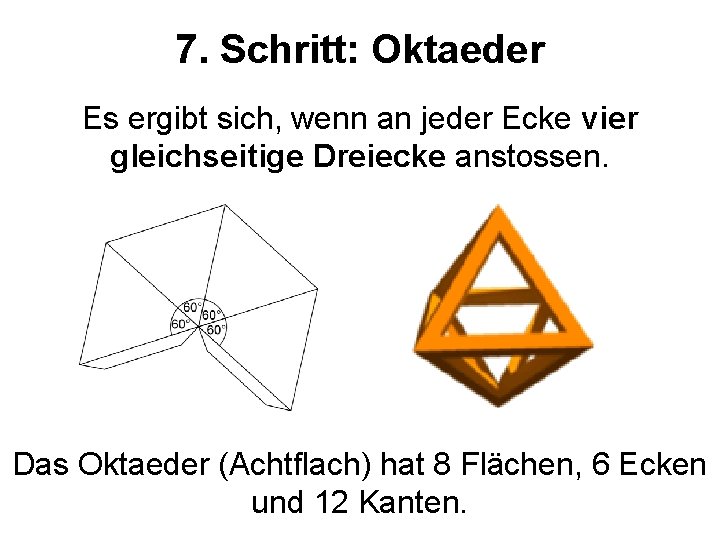
7. Schritt: Oktaeder Es ergibt sich, wenn an jeder Ecke vier gleichseitige Dreiecke anstossen. Das Oktaeder (Achtflach) hat 8 Flächen, 6 Ecken und 12 Kanten.

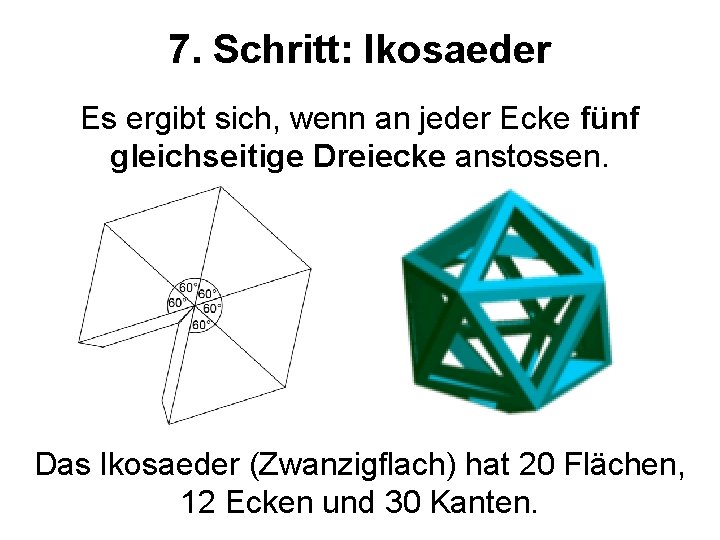
7. Schritt: Ikosaeder Es ergibt sich, wenn an jeder Ecke fünf gleichseitige Dreiecke anstossen. Das Ikosaeder (Zwanzigflach) hat 20 Flächen, 12 Ecken und 30 Kanten.

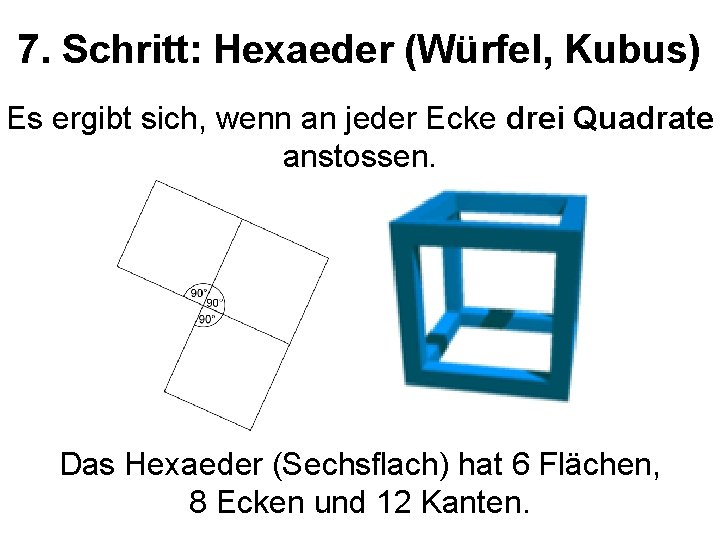
7. Schritt: Hexaeder (Würfel, Kubus) Es ergibt sich, wenn an jeder Ecke drei Quadrate anstossen. Das Hexaeder (Sechsflach) hat 6 Flächen, 8 Ecken und 12 Kanten.

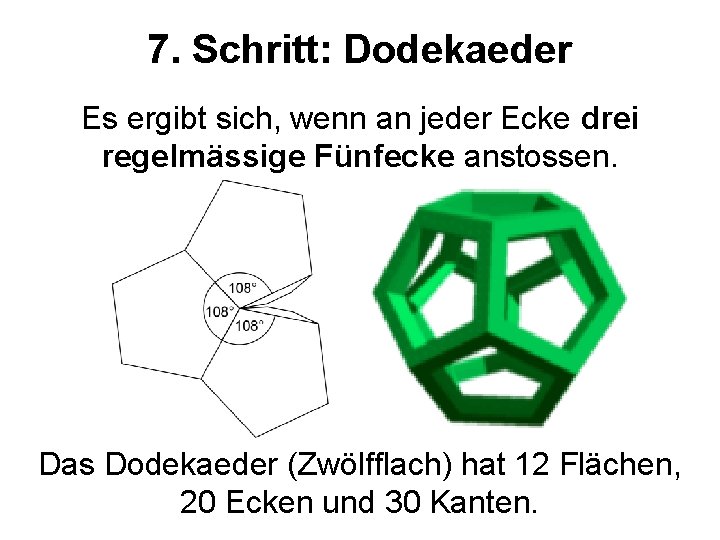
7. Schritt: Dodekaeder Es ergibt sich, wenn an jeder Ecke drei regelmässige Fünfecke anstossen. Das Dodekaeder (Zwölfflach) hat 12 Flächen, 20 Ecken und 30 Kanten.

Schlusswort Link zu diesen Folien: http: //www. gymliestal. ch/manuelerdin/Schule/Home. html Ende des Vortrags