Platonic Solids Additional Task to the multimedia book

Platonic Solids Additional Task to the multimedia book „Darstellende Geometrie/ 3 D-Geometry“, published by Veritas Educational Edition Student Edition ISBN - 978 -3 -7058 -9079 -4 ISBN - 978 -3 -7058 -9293 -4 Special edition for teachers: The print version shows handouts of theory and worked-out examples. Each handout can be printed in colour and is also suitable as a solutions handout. Through the use of animated Power. Point files it is possible to structure the lessons in a contemporary and innovative manner for students. Special edition for students: The print version consists of well prepared worksheets to start working right away. On the CD you will find colourful Power. Point presentations, including theory as well as solved examples with step-by-step explanations. This provides a highly efficient technique in developing an understanding of geometry and its concepts. for more DETAILS and ORDER 1

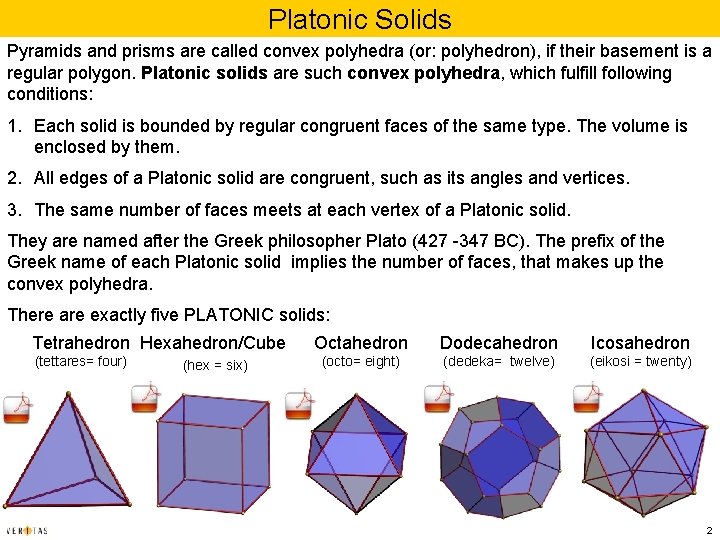
Platonic Solids Pyramids and prisms are called convex polyhedra (or: polyhedron), if their basement is a regular polygon. Platonic solids are such convex polyhedra, which fulfill following conditions: 1. Each solid is bounded by regular congruent faces of the same type. The volume is enclosed by them. 2. All edges of a Platonic solid are congruent, such as its angles and vertices. 3. The same number of faces meets at each vertex of a Platonic solid. They are named after the Greek philosopher Plato (427 -347 BC). The prefix of the Greek name of each Platonic solid implies the number of faces, that makes up the convex polyhedra. There are exactly five PLATONIC solids: Tetrahedron Hexahedron/Cube (tettares= four) (hex = six) Octahedron Dodecahedron Icosahedron (octo= eight) (dedeka= twelve) (eikosi = twenty) 2

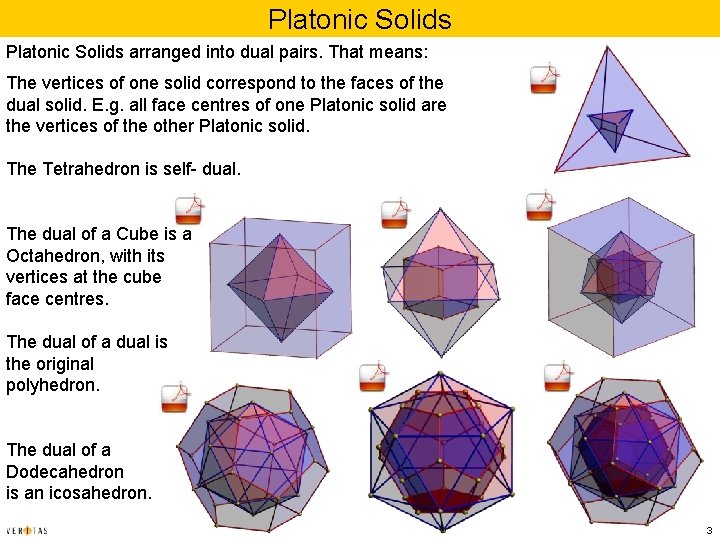
Platonic Solids arranged into dual pairs. That means: The vertices of one solid correspond to the faces of the dual solid. E. g. all face centres of one Platonic solid are the vertices of the other Platonic solid. The Tetrahedron is self- dual. The dual of a Cube is a Octahedron, with its vertices at the cube face centres. The dual of a dual is the original polyhedron. The dual of a Dodecahedron is an icosahedron. 3

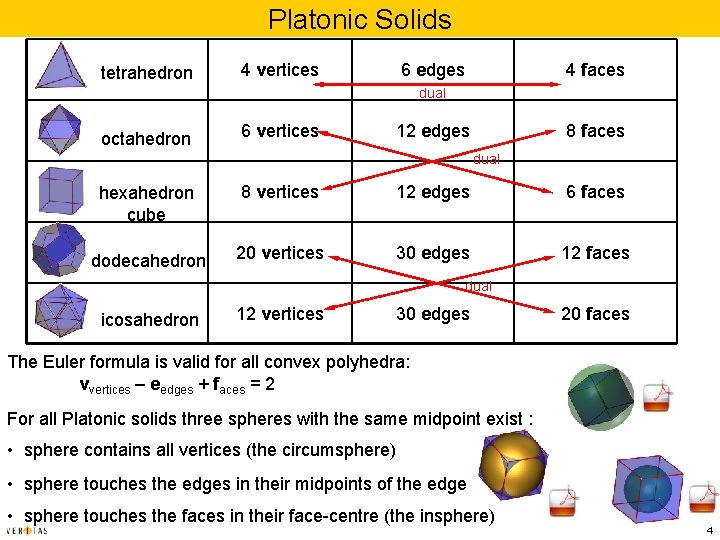
Platonic Solids tetrahedron 4 vertices 6 edges 4 faces dual octahedron 6 vertices 12 edges 8 faces dual hexahedron cube 8 vertices 12 edges 6 faces dodecahedron 20 vertices 30 edges 12 faces dual icosahedron 12 vertices 30 edges 20 faces The Euler formula is valid for all convex polyhedra: vvertices – eedges + faces = 2 For all Platonic solids three spheres with the same midpoint exist : • sphere contains all vertices (the circumsphere) • sphere touches the edges in their midpoints of the edge • sphere touches the faces in their face-centre (the insphere) 4

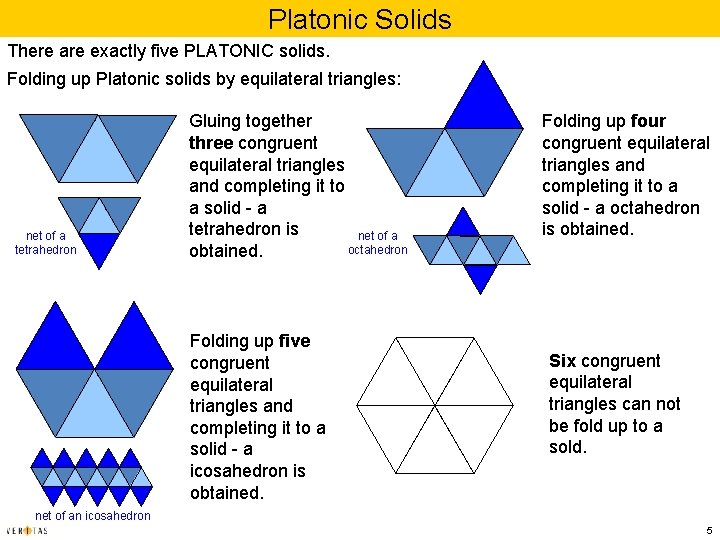
Platonic Solids There are exactly five PLATONIC solids. Folding up Platonic solids by equilateral triangles: net of a tetrahedron Gluing together three congruent equilateral triangles and completing it to a solid - a tetrahedron is net of a octahedron obtained. Folding up five congruent equilateral triangles and completing it to a solid - a icosahedron is obtained. Folding up four congruent equilateral triangles and completing it to a solid - a octahedron is obtained. Six congruent equilateral triangles can not be fold up to a sold. net of an icosahedron 5

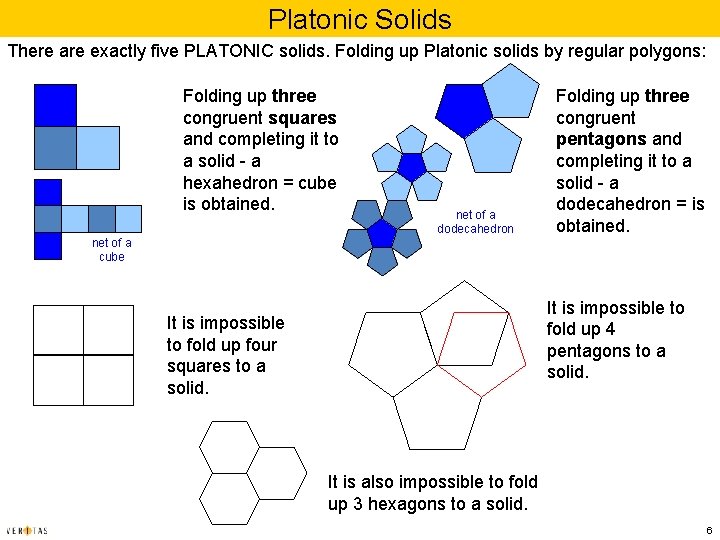
Platonic Solids There are exactly five PLATONIC solids. Folding up Platonic solids by regular polygons: Folding up three congruent squares and completing it to a solid - a hexahedron = cube is obtained. net of a dodecahedron Folding up three congruent pentagons and completing it to a solid - a dodecahedron = is obtained. net of a cube It is impossible to fold up 4 pentagons to a solid. It is impossible to fold up four squares to a solid. It is also impossible to fold up 3 hexagons to a solid. 6

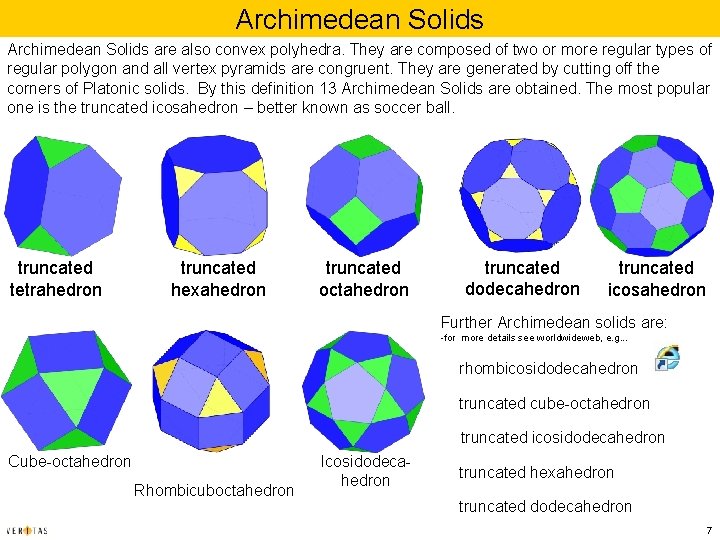
Archimedean Solids are also convex polyhedra. They are composed of two or more regular types of regular polygon and all vertex pyramids are congruent. They are generated by cutting off the corners of Platonic solids. By this definition 13 Archimedean Solids are obtained. The most popular one is the truncated icosahedron – better known as soccer ball. truncated tetrahedron truncated hexahedron truncated octahedron truncated dodecahedron truncated icosahedron Further Archimedean solids are: -for more details see worldwideweb, e. g. . . rhombicosidodecahedron truncated cube-octahedron truncated icosidodecahedron Cube-octahedron Rhombicuboctahedron Icosidodecahedron truncated hexahedron truncated dodecahedron 7