Planning operation start times for the manufacture of

Planning operation start times for the manufacture of capital products with uncertain processing times and resource constraints D. P. Song, Dr. C. Hicks & Dr. C. F. Earl Department of MMM Engineering University of Newcastle upon Tyne ISAC, Newcastle upon Tyne, on 8 -10 Sept. , 2000.

Overview 1. Introduction 2. Problem formulation 3. Perturbation Analysis (PA) method 4. Simulated Annealing (SA) method 5. Case studies 6. Conclusions

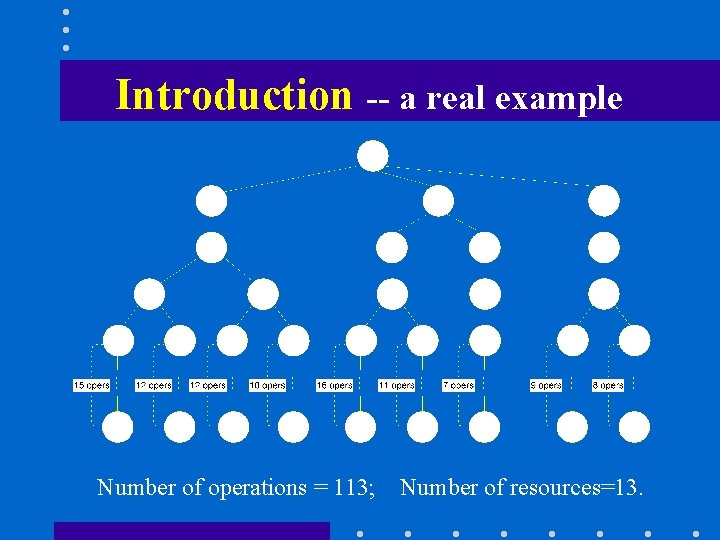
Introduction -- a real example Number of operations = 113; Number of resources=13.

Introduction -- a simple example Final assembly Subassembly Component

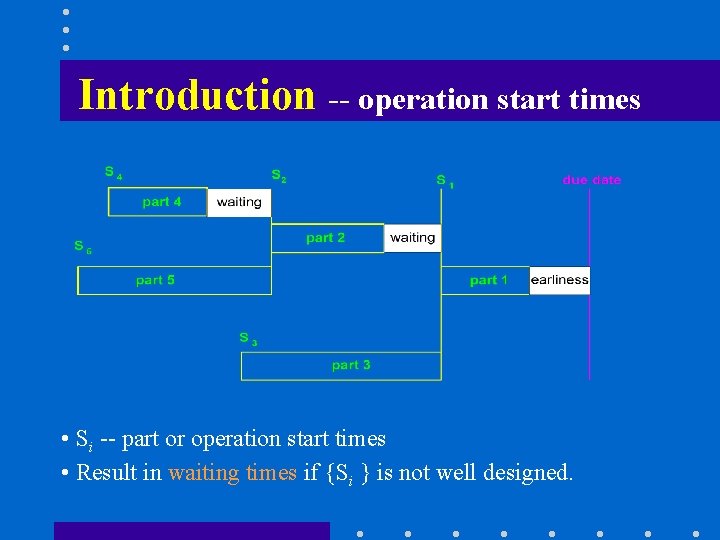
Introduction -- operation start times • Si -- part or operation start times • Result in waiting times if {Si } is not well designed.

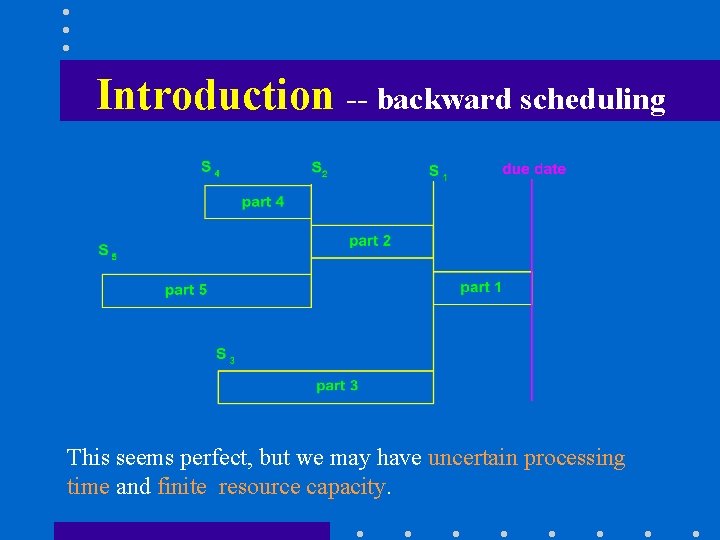
Introduction -- backward scheduling This seems perfect, but we may have uncertain processing time and finite resource capacity.

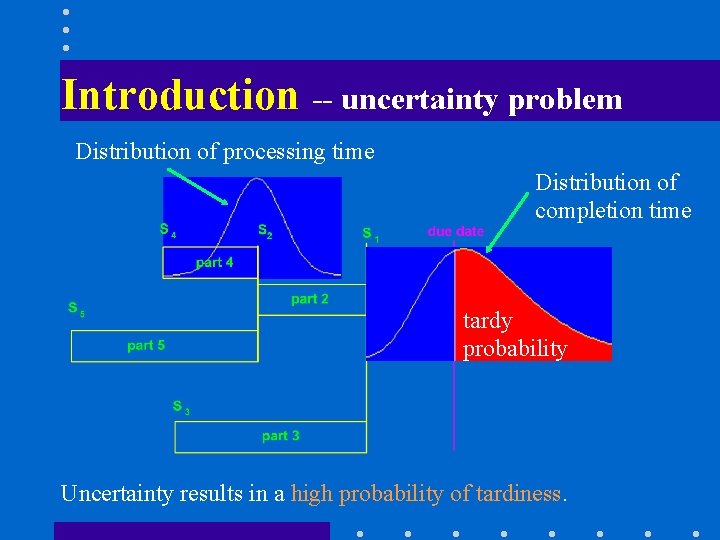
Introduction -- uncertainty problem Distribution of processing time Distribution of completion time tardy probability Uncertainty results in a high probability of tardiness.

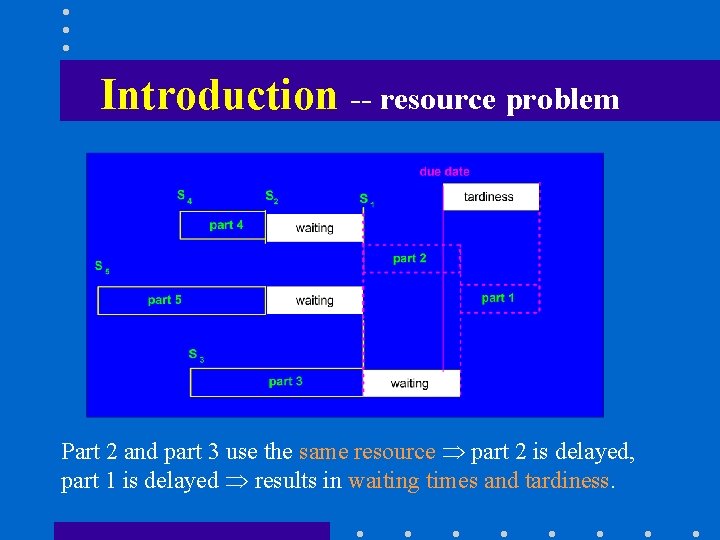
Introduction -- resource problem Part 2 and part 3 use the same resource Þ part 2 is delayed, part 1 is delayed Þ results in waiting times and tardiness.

Problem formulation • Find optimal S=(S 1, S 2, …, Sn) to minimise expected total cost: J(S) = E{S(WIP holding costs + product earliness costs + product tardiness costs)} • Assumption: operation sequences are fixed. • Key step of Stochastic Approximation is: ¶J(S)/¶Si = ?

Perturbation analysis -- general problem • Consider to minimise: J(q) = EL(q, w) J(. ) -- system performance index. L(. ) -- sample performance function. q -- a vector of n real parameters. w -- a realization of the set of random sequences. • PA aims to find an unbiased estimator of gradient -- ¶J(q)/¶qi , with as little computation as possible.

Perturbation analysis -- main idea • Based on a single sample realization • Using theoretical analysis • Calculate ¶L(q, w)/¶qi , i = 1, 2, …, n sample function gradient • Exchange E and ¶: ? E¶L(q, w)/¶qi = ¶EL(q, w)/¶qi = ¶J(q)/¶qi

PA algorithm -- concepts • Two concepts: nominal path and perturbed path • Sample realization for {Si}-- nominal path (NP) • Sample realization for {Si+D, Sj, j¹i} -- perturbed path (PP), where D is sufficiently small. • All perturbed paths are theoretically constructed from NP rather than from new experiments

PA algorithm -- Perturbation rules • Perturbation generation rule -- When PP starts to deviate from NP ? • Perturbation propagation rule -- How the perturbation of one part affects the processing of other parts? -- along the critical paths -- along the critical resources • Perturbation disappearance rule -- When PP and NP overlaps again ?

PA algorithm -- Perturbation rules • If S 2 is perturbed to be S 2+ D. perturbation generation • Cost changes due to the perturbation disappearance

PA algorithm -- Perturbation rules • If S 3 is perturbed to be S 3+ D. • Cost changes due to the perturbation generation perturbation propagation

PA algorithm -- gradient estimate • From PP and NP calculate sample function gradient : ¶L(S, w)/¶Si -- usually can be expressed by indicator functions. • Unbiasedness of gradient estimator: E¶L(S, w)/¶Si = ¶J(S)/¶Si Condition: processing times are independent continuous random variables.

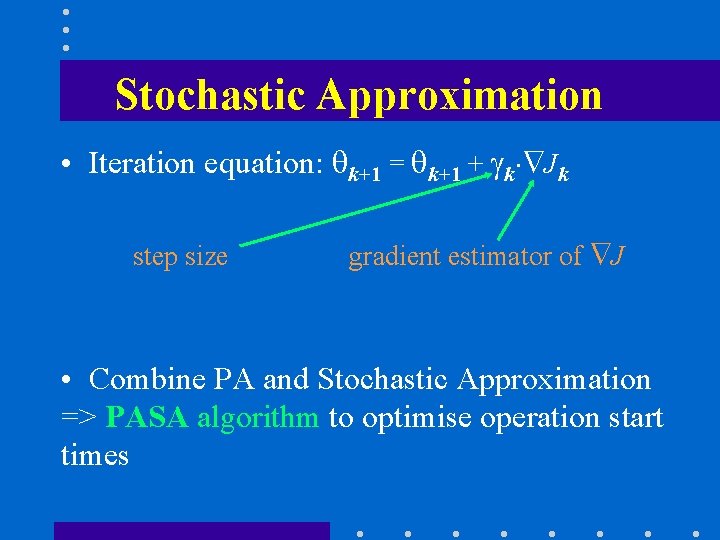
Stochastic Approximation • Iteration equation: qk+1 = qk+1 + gk× Jk step size gradient estimator of J • Combine PA and Stochastic Approximation => PASA algorithm to optimise operation start times

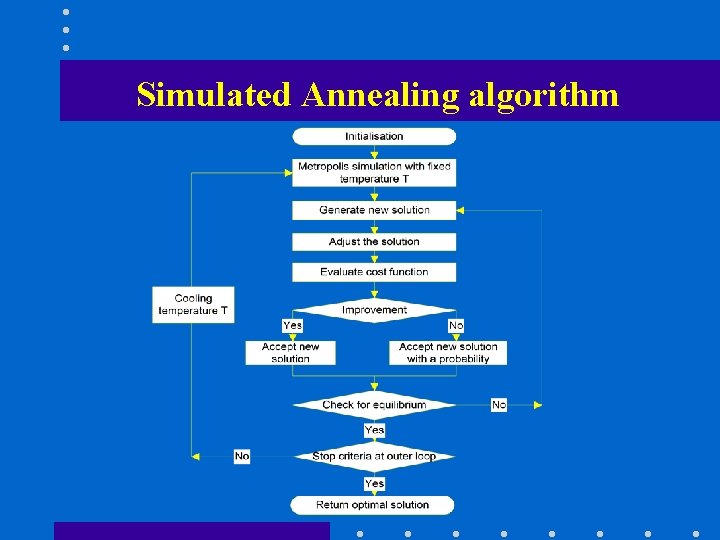
Simulated Annealing algorithm • Random local search method • Ability to approximate the global optimum • Outer loop -- cooling temperature (T) until T=0. • Inner loop -- perform Metropolis simulation with fixed T to find equilibrium state

Simulated Annealing algorithm • In our problem, a solution = (S 1, S 2, …, Sn). • A neighborhood of a solution can be obtained by making changes in Si. • New solution is adjusted to meet precedence and resource constraints; non-negative. • Cost is evaluated by averaging a set of sample processes.

Simulated Annealing algorithm

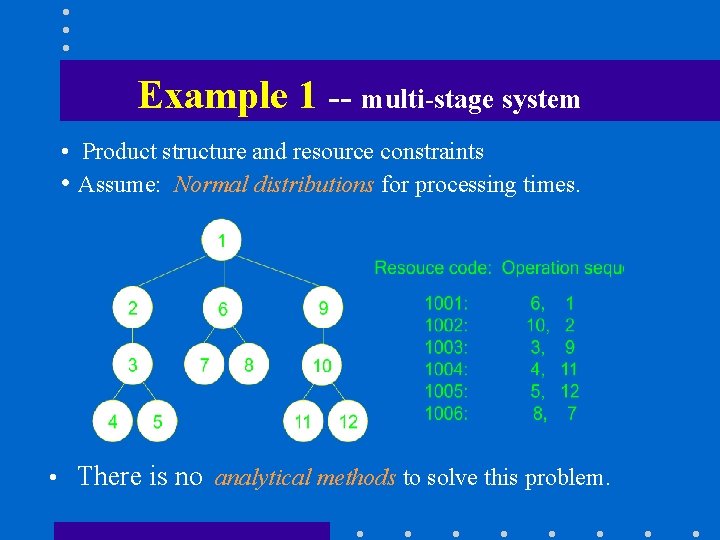
Example 1 -- multi-stage system • Product structure and resource constraints • Assume: Normal distributions for processing times. • There is no analytical methods to solve this problem.

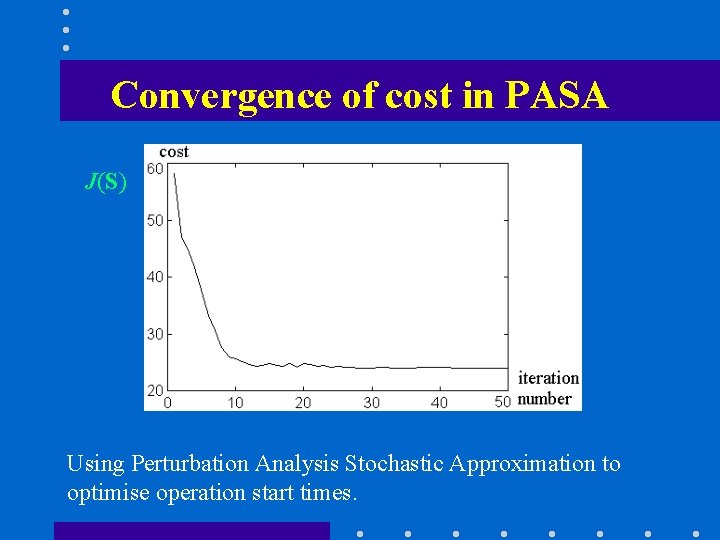
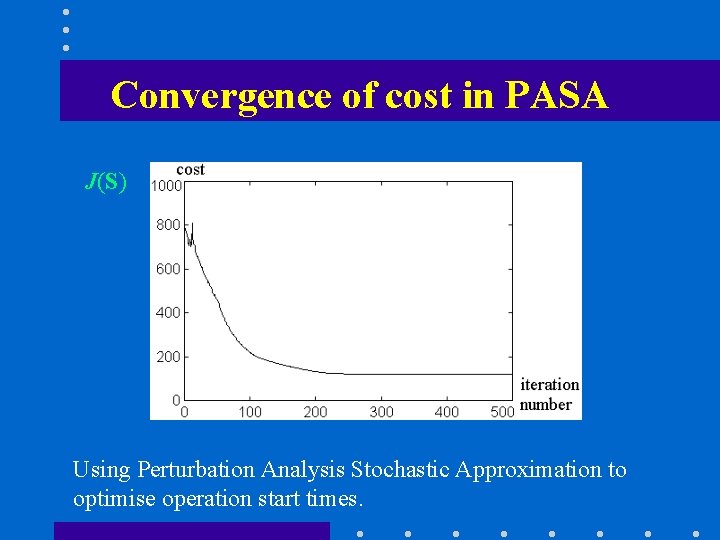
Convergence of cost in PASA J(S) Using Perturbation Analysis Stochastic Approximation to optimise operation start times.

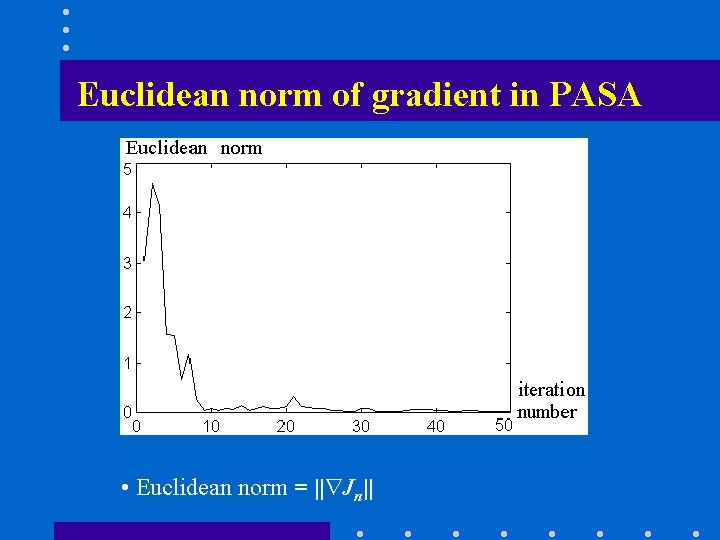
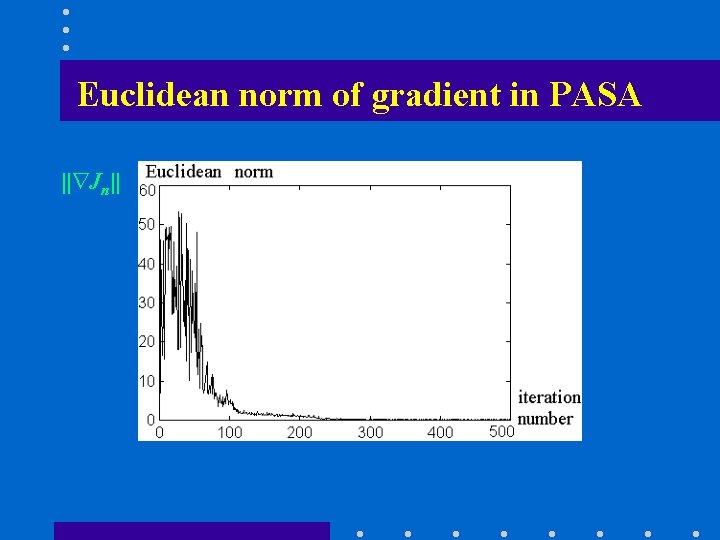
Euclidean norm of gradient in PASA • Euclidean norm = || Jn||

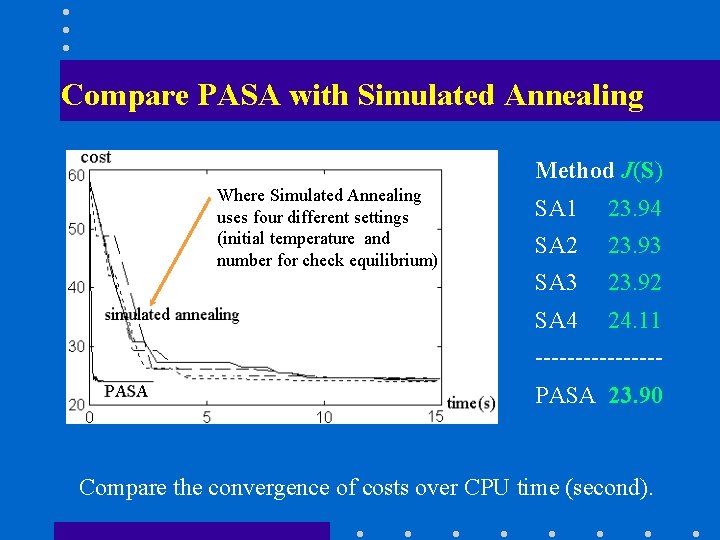
Compare PASA with Simulated Annealing Method J(S) Where Simulated Annealing uses four different settings (initial temperature and number for check equilibrium) SA 1 23. 94 SA 2 23. 93 SA 3 23. 92 SA 4 24. 11 --------PASA 23. 90 Compare the convergence of costs over CPU time (second).

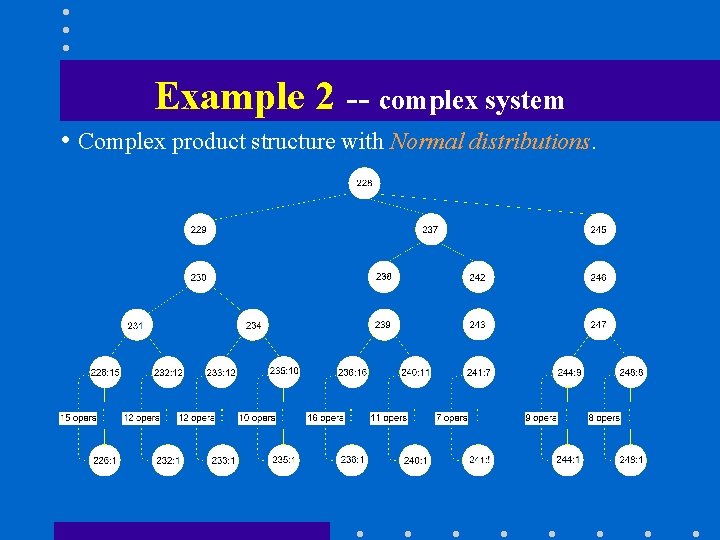
Example 2 -- complex system • Complex product structure with Normal distributions.

Resource constraints Resources Operation sequences 1000: 247, 243, 239, 234, 231, 246, 242, 238, 230, 245, 237, 229, 228. 1211: 236: 1, 236: 2, 236: 3, 236: 4, 236: 5, 236: 6, 236: 7, 226: 1, 236: 8, 226: 2, 226: 3, 226: 4, 226: 5, 226: 6, 236: 11, 226: 7, 232: 1, 226: 8, 235: 1, 232: 2, 236: 12, 235: 2, 226: 9, 232: 3, 235: 3, 240: 1, 235: 4, 240: 2, 226: 10, 232: 5, 236: 13, 233: 2, 235: 5, 240: 3, 233: 3, 235: 6, 240: 4, 232: 7, 226: 11, 233: 4, 235: 7, 240: 5, 232: 8, 233: 5, 235: 8, 240: 6, 232: 9, 233: 6, 240: 7, 226: 12, 232: 10, 235: 9, 240: 8, 233: 8, 240: 9, 233: 9, 226: 13, 235: 10, 240: 10, 236: 15, 226: 14, 240: 11, 236: 16, 226: 15. 1212: 236: 9, 236: 10, 232: 4, 232: 6, 236: 14, 232: 11, 232: 12. 1511: 233: 1, 233: 7, 233: 11.

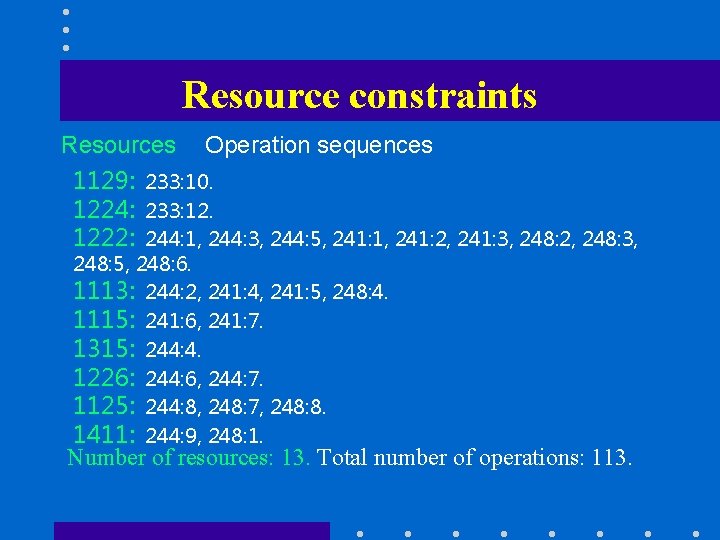
Resource constraints Resources Operation sequences 1129: 233: 10. 1224: 233: 12. 1222: 244: 1, 244: 3, 244: 5, 241: 1, 241: 2, 241: 3, 248: 2, 248: 3, 248: 5, 248: 6. 1113: 244: 2, 241: 4, 241: 5, 248: 4. 1115: 241: 6, 241: 7. 1315: 244: 4. 1226: 244: 6, 244: 7. 1125: 244: 8, 248: 7, 248: 8. 1411: 244: 9, 248: 1. Number of resources: 13. Total number of operations: 113.

Convergence of cost in PASA J(S) Using Perturbation Analysis Stochastic Approximation to optimise operation start times.

Euclidean norm of gradient in PASA || Jn||

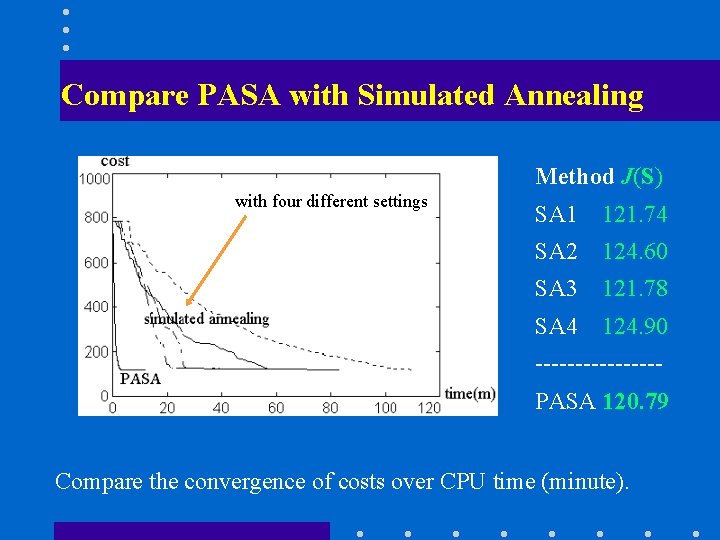
Compare PASA with Simulated Annealing Method J(S) with four different settings SA 1 121. 74 SA 2 124. 60 SA 3 121. 78 SA 4 124. 90 --------PASA 120. 79 Compare the convergence of costs over CPU time (minute).

Conclusions • Both PASA and SA can deal with complex systems beyond the ability of analytical methods. • PASA is much faster and yields better solutions than Simulated Annealing in case studies • SA is more robust and flexible, does not require any assumption on uncertainty

Further Work • Optimise both operation sequences and start times • Integrate Perturbation Analysis with SA or Evolution algorithms • Extend to dynamic planning problems such as incremental planning and re-planning