Planning Graph Based Reachability Heuristics Daniel Bryce Subbarao

Planning Graph Based Reachability Heuristics Daniel Bryce & Subbarao Kambhampati ICAPS’ 06 Tutorial 6 June 7, 2006 http: //rakaposhi. eas. asu. edu/pg-tutorial/ dan. bryce@asu. edu rao@asu. edu, June 7 th, 2006 http: //verde. eas. asu. edu http: //rakaposhi. eas. asu. edu ICAPS'06 Tutorial T 6

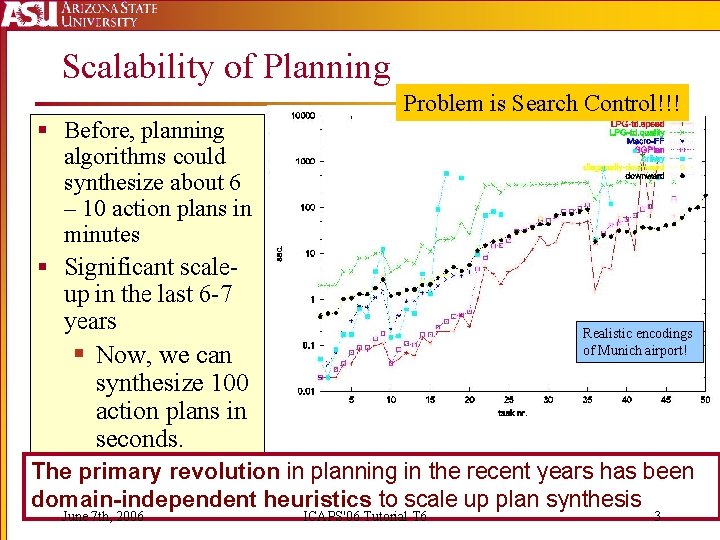
Scalability of Planning Problem is Search Control!!! § Before, planning algorithms could synthesize about 6 – 10 action plans in minutes § Significant scaleup in the last 6 -7 years Realistic encodings of Munich airport! § Now, we can synthesize 100 action plans in seconds. The primary revolution in planning in the recent years has been domain-independent heuristics to scale up plan synthesis June 7 th, 2006 ICAPS'06 Tutorial T 6 3

Motivation § Ways to improve Planner Scalability § Problem Formulation § Search Space § Reachability Heuristics § Domain (Formulation) Independent § Work for many search spaces § Flexible – work with most domain features § Overall complement other scalability techniques § Effective!! June 7 th, 2006 ICAPS'06 Tutorial T 6 4

Topics § § § § § Classical Planning Cost Based Planning Rao Partial Satisfaction Planning <Break> Non-Deterministic/Probabilistic Planning Resources (Continuous Quantities) Temporal Planning Hybrid Models Wrap-up Rao June 7 th, 2006 ICAPS'06 Tutorial T 6 Dan 5

Classical Planning June 7 th, 2006 ICAPS'06 Tutorial T 6 6

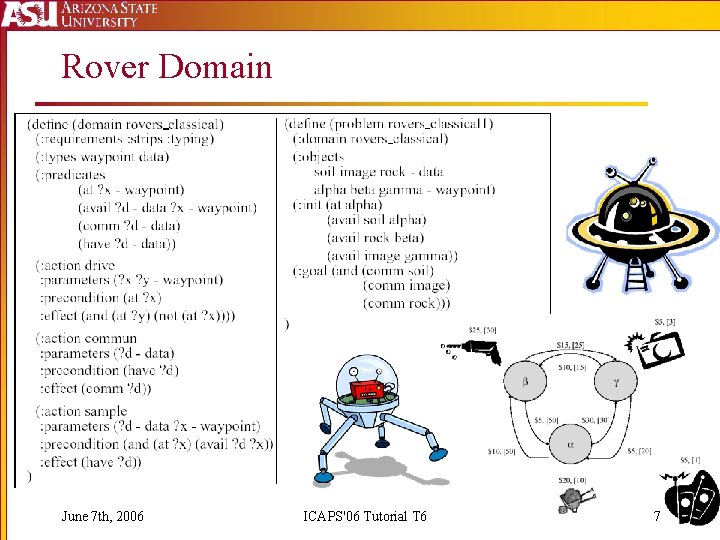
Rover Domain June 7 th, 2006 ICAPS'06 Tutorial T 6 7

Classical Planning § Relaxed Reachability Analysis § Types of Heuristics § Level-based § Relaxed Plans § Mutexes § Heuristic Search § Progression § Regression § Plan Space § Exploiting Heuristics June 7 th, 2006 ICAPS'06 Tutorial T 6 8

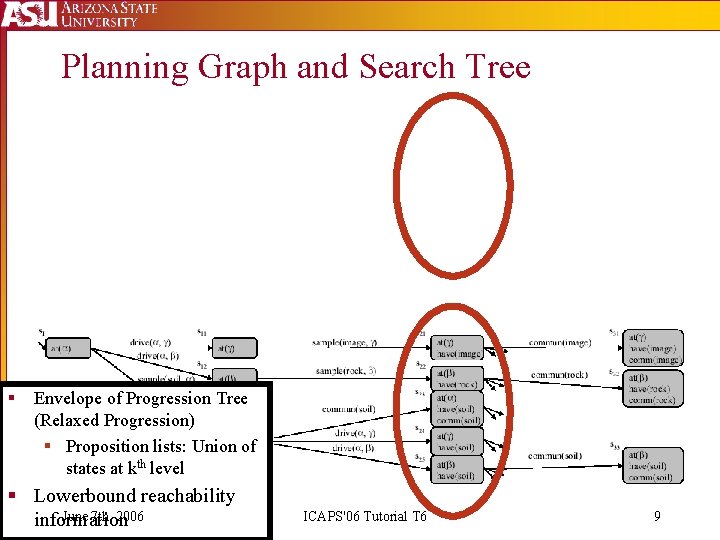
Planning Graph and Search Tree § Envelope of Progression Tree (Relaxed Progression) § Proposition lists: Union of states at kth level § Lowerbound reachability June 7 th, 2006 information ICAPS'06 Tutorial T 6 9

Level Based Heuristics § The distance of a proposition is the index of the first proposition layer in which it appears § Proposition distance changes when we propagate cost functions – described later § What is the distance of a Set of propositions? ? § Set-Level: Index of first proposition layer where all goal propositions appear § Admissible § Gets better with mutexes, otherwise same as max § Max: Maximum distance proposition § Sum: Summation of proposition distances June 7 th, 2006 ICAPS'06 Tutorial T 6 10

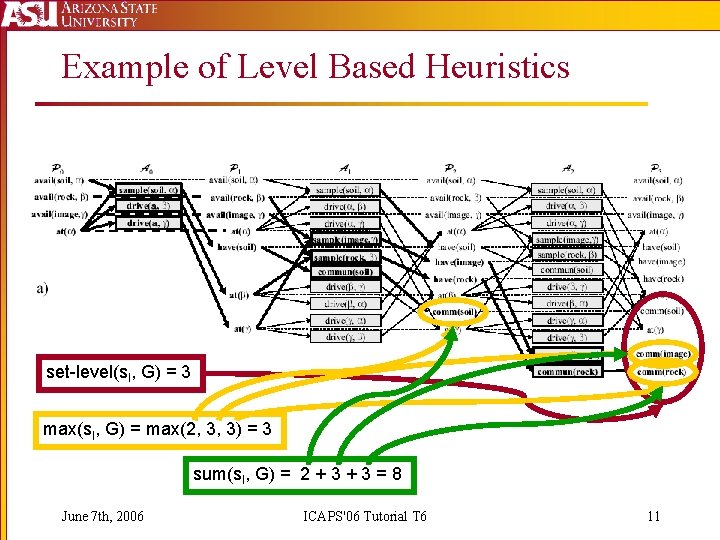
Example of Level Based Heuristics set-level(s. I, G) = 3 max(s. I, G) = max(2, 3, 3) = 3 sum(s. I, G) = 2 + 3 = 8 June 7 th, 2006 ICAPS'06 Tutorial T 6 11

Distance of a Set of Literals Admissible h(S) = p S lev({p}) Sum Partition-k § § Adjusted Sum h(S) = lev(S) Set-Level Combo Set-Level with memos lev(p) : index of the first level at which p comes into the planning graph lev(S): index of the first level where all props in S appear non-mutexed. § If there is no such level, then If the graph is grown to level off, then Else k+1 (k is the current length of the graph) June 7 th, 2006 ICAPS'06 Tutorial T 6 12

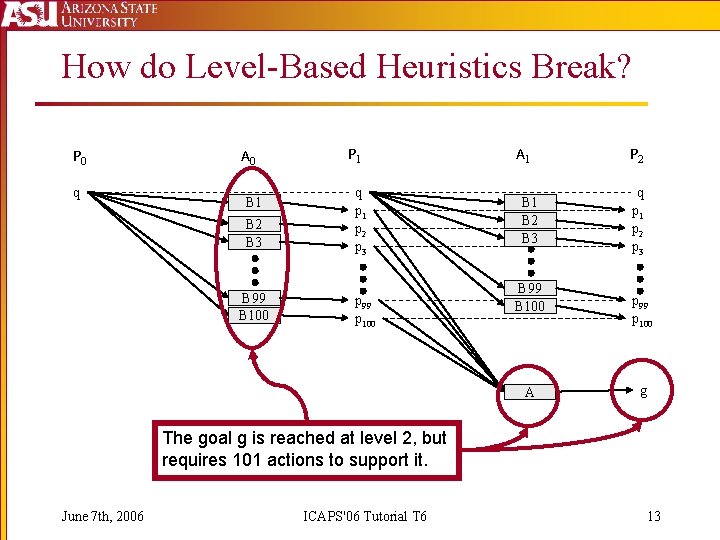
How do Level-Based Heuristics Break? P 0 q A 0 B 1 B 2 B 3 B 99 B 100 P 1 q p 1 p 2 p 3 p 99 p 100 A 1 B 2 B 3 B 99 B 100 A P 2 q p 1 p 2 p 3 p 99 p 100 g The goal g is reached at level 2, but requires 101 actions to support it. June 7 th, 2006 ICAPS'06 Tutorial T 6 13

Relaxed Plan Heuristics § When Level does not reflect distance well, we can find a relaxed plan. § A relaxed plan is subgraph of the planning graph, where: § Every goal proposition is in the relaxed plan at the level where it first appears § Every proposition in the relaxed plan has a supporting action in the relaxed plan § Every action in the relaxed plan has its preconditions supported. § Relaxed Plans are not admissible, but are generally effective. § Finding the optimal relaxed plan is NP-hard, but finding a greedy one is easy. Later we will see how “greedy” can change. June 7 th, 2006 ICAPS'06 Tutorial T 6 14

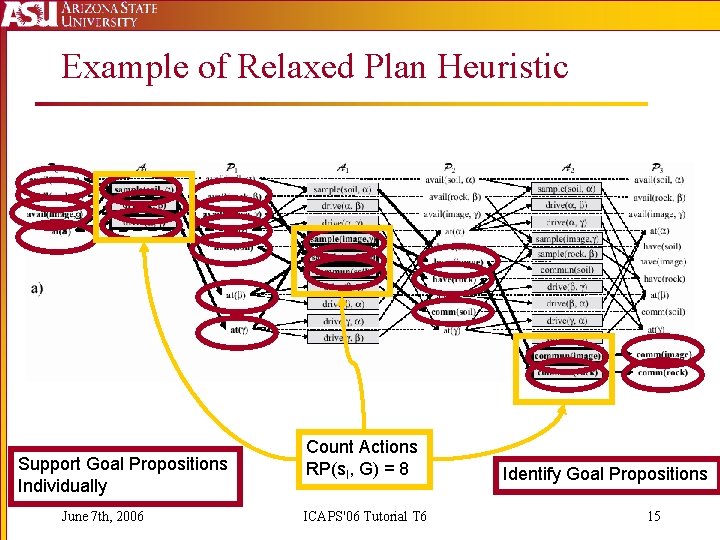
Example of Relaxed Plan Heuristic Support Goal Propositions Individually June 7 th, 2006 Count Actions RP(s. I, G) = 8 ICAPS'06 Tutorial T 6 Identify Goal Propositions 15

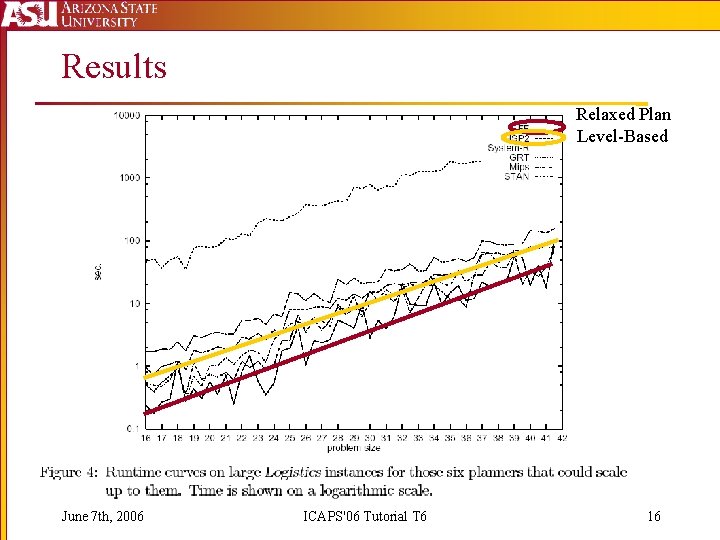
Results Relaxed Plan Level-Based June 7 th, 2006 ICAPS'06 Tutorial T 6 16

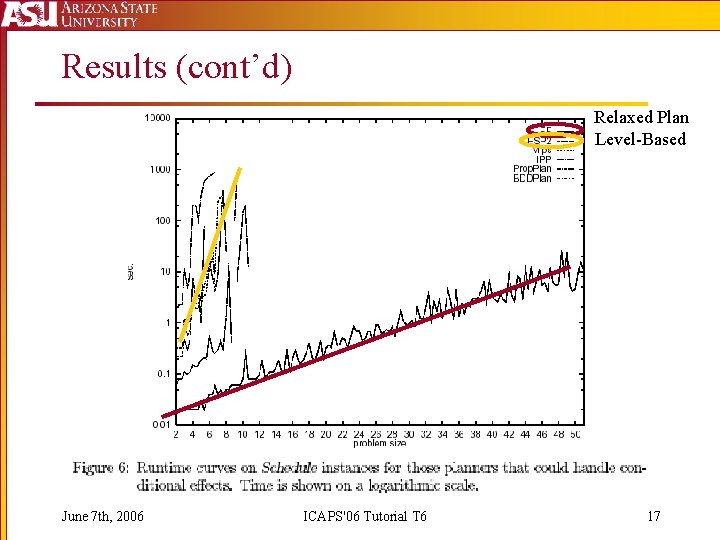
Results (cont’d) Relaxed Plan Level-Based June 7 th, 2006 ICAPS'06 Tutorial T 6 17

Optimizations in Heuristic Computation § Taming Space/Time costs § Bi-level Planning Graph representation § Partial expansion of the PG (stop before level-off) § It is FINE to cut corners when using PG for heuristics (instead of search)!! § Branching factor can still be quite high § Use actions appearing in the PG (complete) § Select actions in lev(S) vs Levels-off (incomplete) § Consider action appearing in RP June 7 th, 2006 ICAPS'06 Tutorial T 6 (incomplete) 18

Adjusting for Negative Interactions § Until now we assumed actions only positively interact. What about negative interactions? § Mutexes help us capture some negative interactions § Types § Actions: Interference/Competing Needs § Propositions: Inconsistent Support § Binary are the most common and practical § |A| + 2|P|-ary will allow us to solve the planning problem with a backtrack-free Graph. Plan search § An action layer may have |A| actions and 2|P| noops § Serial Planning Graph assumes all non-noop actions are mutex June 7 th, 2006 ICAPS'06 Tutorial T 6 19

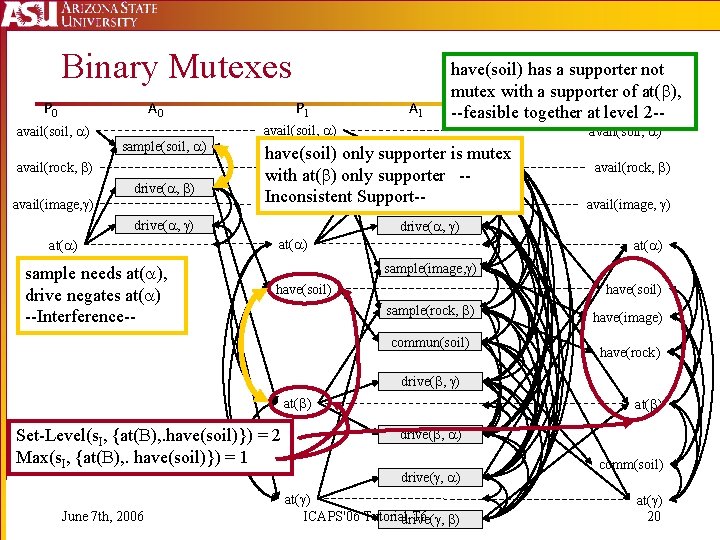
Binary Mutexes P 0 A 0 avail(soil, ) sample(soil, ) avail(rock, ) drive( , ) avail(image, ) P 1 avail(soil, ) sample(soil, ) have(soil) only supporter is mutex avail(rock, ) with at( ) only supporter -drive( , ) Inconsistent Support-avail(image, ) drive( , ) at( ) sample needs at( ), drive negates at( ) --Interference-- A 1 have(soil) has a supporter not mutex with a supporter of at( ), P 2 2 ---feasible together at level avail(soil, ) avail(rock, ) avail(image, ) drive( , ) at( ) sample(image, ) have(soil) sample(rock, ) commun(soil) have(image) have(rock) drive( , ) at( ) Set-Level(s. I, {at( ), . have(soil)}) = 2 Max(s. I, {at( ), . have(soil)}) = 1 June 7 th, 2006 at( ) drive( , ) at( ) ICAPS'06 Tutorialdrive( , T 6 ) comm(soil) at( ) 20

Adjusting the Relaxed Plans § Start with RP heuristic and adjust it to take subgoal interactions into account § Negative interactions in terms of “degree of interaction” § Positive interactions in terms of co-achievement links § Ignore negative interactions when accounting for positive interactions (and vice versa) HAdj. Sum 2 M(S) = length(Relaxed. Plan(S)) + max p, q S (p, q) Where (p, q) = lev({p, q}) - max{lev(p), lev(q)} /*Degree of –ve Interaction */ June 7 th, 2006 ICAPS'06 Tutorial T 6 [AAAI 2000] 21

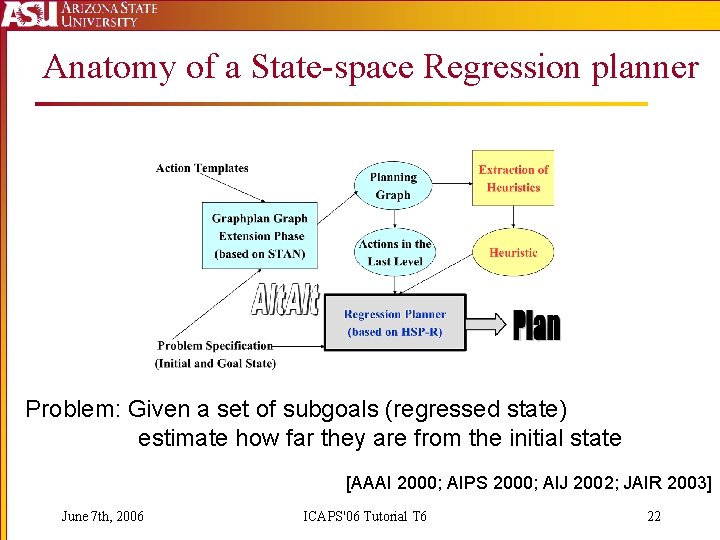
Anatomy of a State-space Regression planner Problem: Given a set of subgoals (regressed state) estimate how far they are from the initial state [AAAI 2000; AIPS 2000; AIJ 2002; JAIR 2003] June 7 th, 2006 ICAPS'06 Tutorial T 6 22

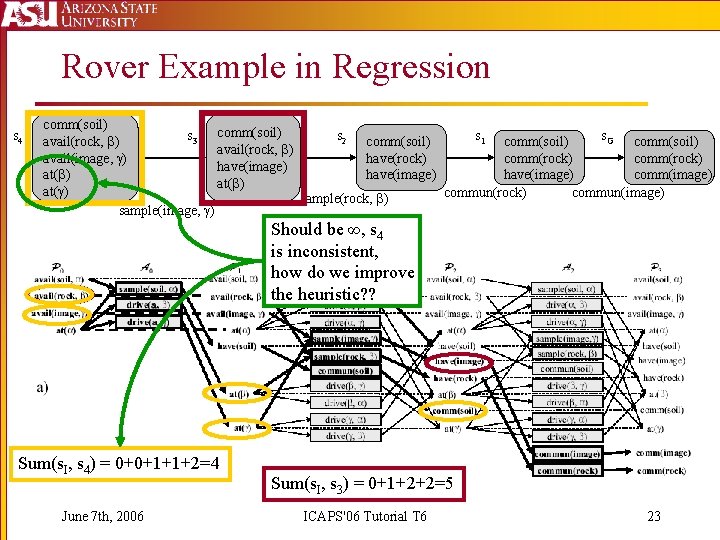
Rover Example in Regression s 4 comm(soil) s 3 comm(soil) s 2 comm(soil) s 1 comm(soil) s. G comm(soil) avail(rock, ) have(rock) avail(image, ) comm(rock) have(image) at( ) have(image) comm(image) at( ) commun(rock) commun(image) sample(rock, ) sample(image, ) Should be ∞, s 4 is inconsistent, how do we improve the heuristic? ? Sum(s. I, s 4) = 0+0+1+1+2=4 June 7 th, 2006 Sum(s. I, s 3) = 0+1+2+2=5 ICAPS'06 Tutorial T 6 23

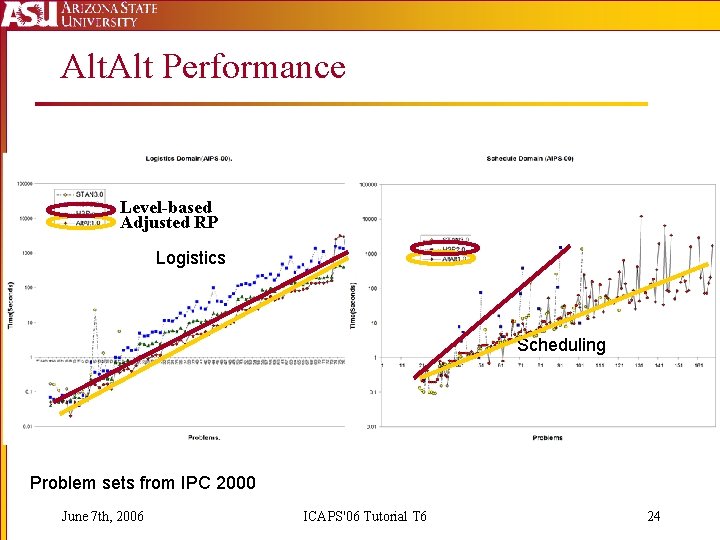
Alt. Alt Performance Level-based Adjusted RP Logistics Scheduling Problem sets from IPC 2000 June 7 th, 2006 ICAPS'06 Tutorial T 6 24

Plan Space Search Then it was cruelly Un. POPped The good times return with Re(vived)POP In the beginning it was all POP. June 7 th, 2006 ICAPS'06 Tutorial T 6 25

POP Algorithm 1. Plan Selection: Select a plan P from the search queue 2. Flaw Selection: Choose a flaw f (open cond or unsafe link) 3. Flaw resolution: If f is an open condition, choose an action S that achieves f If f is an unsafe link, choose promotion or demotion Update P Return NULL if no resolution exist 4. If there is no flaw left, return P 1. Initial plan: g 1 g 2 Sinf S 0 2. Plan refinement (flaw selection and resolution): q 1 S 0 p S 1 oc 2 S 3 g 2 g 1 Sinf g 2 ~p Choice points • Flaw selection (open condition? unsafe link? Non-backtrack choice) • Flaw resolution/Plan Selection (how to select (rank) partial plan? ) June 7 th, 2006 ICAPS'06 Tutorial T 6 26

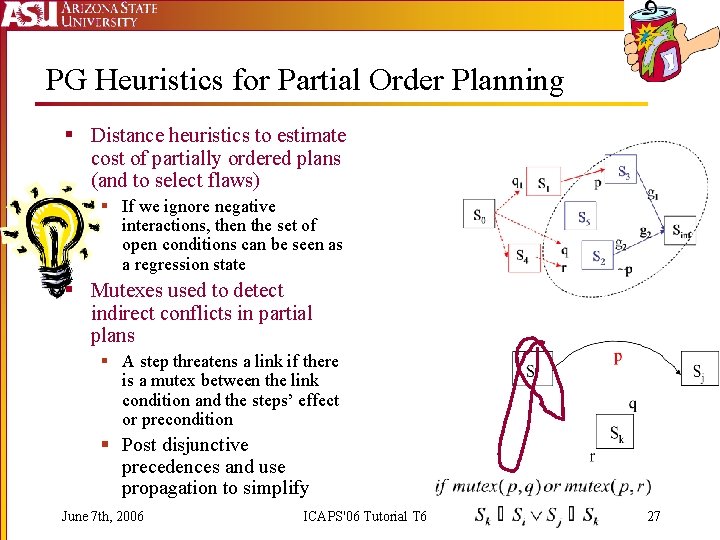
PG Heuristics for Partial Order Planning § Distance heuristics to estimate cost of partially ordered plans (and to select flaws) § If we ignore negative interactions, then the set of open conditions can be seen as a regression state § Mutexes used to detect indirect conflicts in partial plans § A step threatens a link if there is a mutex between the link condition and the steps’ effect or precondition § Post disjunctive precedences and use propagation to simplify June 7 th, 2006 ICAPS'06 Tutorial T 6 27

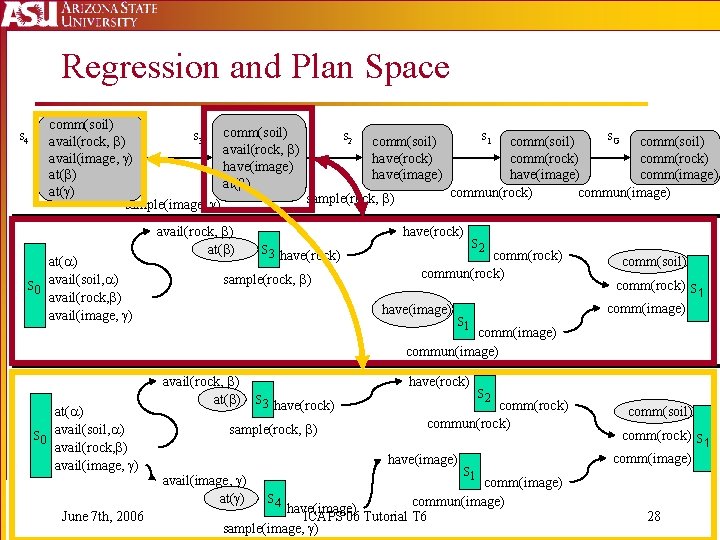
Regression and Plan Space s 4 comm(soil) s 3 comm(soil) s 2 comm(soil) s 1 comm(soil) s. G comm(soil) avail(rock, ) have(rock) avail(image, ) comm(rock) have(image) at( ) have(image) comm(image) at( ) commun(rock) commun(image) sample(rock, ) sample(image, ) at( ) S 0 avail(soil, ) avail(rock, ) avail(image, ) avail(rock, ) at( ) have(rock) S 3 have(rock) sample(rock, ) S 2 comm(rock) commun(rock) have(image) S 1 comm(soil) comm(rock) S 1 comm(image) commun(image) at( ) S 0 avail(soil, ) avail(rock, ) avail(image, ) June 7 th, 2006 avail(rock, ) at( ) have(rock) S 3 have(rock) sample(rock, ) comm(rock) commun(rock) have(image) avail(image, ) at( ) S 2 S 1 comm(image) S 4 commun(image) have(image) ICAPS'06 Tutorial T 6 sample(image, ) comm(soil) comm(rock) S 1 comm(image) 28

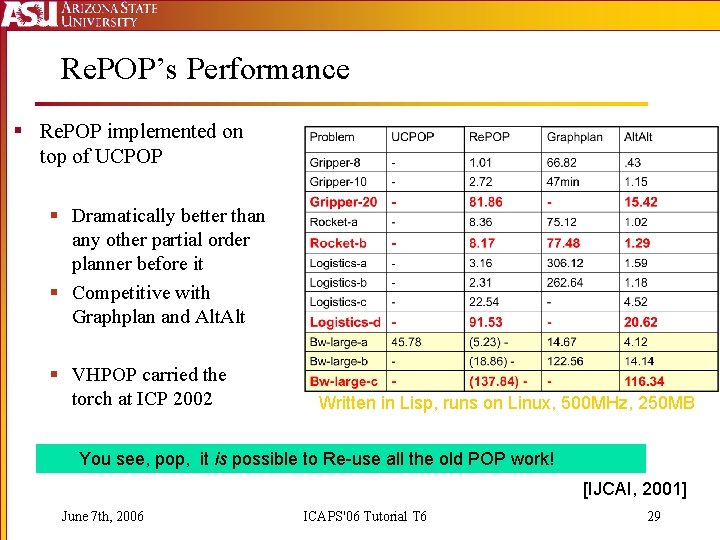
Re. POP’s Performance § Re. POP implemented on top of UCPOP § Dramatically better than any other partial order planner before it § Competitive with Graphplan and Alt § VHPOP carried the torch at ICP 2002 Written in Lisp, runs on Linux, 500 MHz, 250 MB You see, pop, it is possible to Re-use all the old POP work! [IJCAI, 2001] June 7 th, 2006 ICAPS'06 Tutorial T 6 29

Exploiting Planning Graphs § Restricting Action Choice § Use actions from: § § Last level before level off (complete) Last level before goals (incomplete) First Level of Relaxed Plan (incomplete) – FF’s helpful actions Only action sequences in the relaxed plan (incomplete) – YAHSP § Reducing State Representation § Remove static propositions. A static proposition is only ever true or false in the last proposition layer. June 7 th, 2006 ICAPS'06 Tutorial T 6 30

Classical Planning Conclusions § Many Heuristics § Set-Level, Max, Sum, Relaxed Plans § Heuristics can be improved by adjustments § Mutexes § Useful for many types of search § Progresssion, Regression, POCL June 7 th, 2006 ICAPS'06 Tutorial T 6 31

Cost-Based Planning June 7 th, 2006 ICAPS'06 Tutorial T 6 32

Cost-based Planning § Propagating Cost Functions § Cost-based Heuristics § Generalized Level-based heuristics § Relaxed Plan heuristics June 7 th, 2006 ICAPS'06 Tutorial T 6 33

Rover Cost Model June 7 th, 2006 ICAPS'06 Tutorial T 6 34

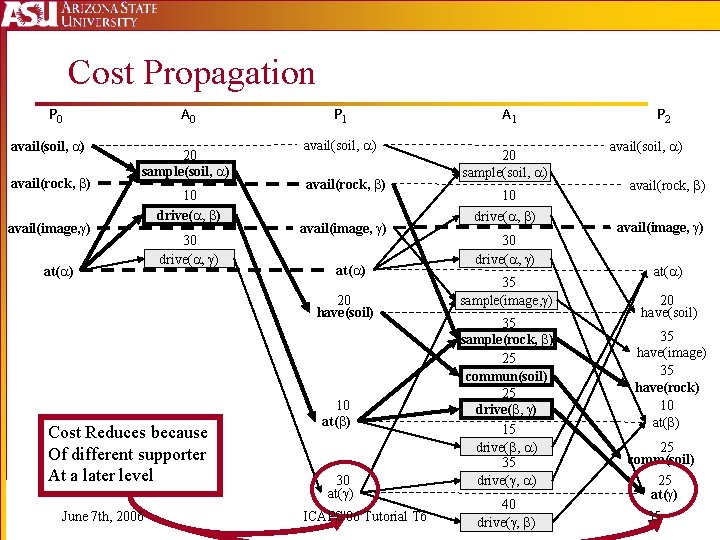
Cost Propagation P 0 avail(soil, ) avail(rock, ) A 0 20 sample(soil, ) avail(image, ) at( ) 10 drive( , ) 30 drive( , ) P 1 avail(soil, ) avail(rock, ) avail(image, ) at( ) 20 have(soil) Cost Reduces because Of different supporter At a later level June 7 th, 2006 10 at( ) 30 at( ) ICAPS'06 Tutorial T 6 A 1 20 sample(soil, ) 10 drive( , ) 35 sample(image, ) 35 sample(rock, ) 25 commun(soil) 25 drive( , ) 15 drive( , ) 35 drive( , ) 40 drive( , ) P 2 avail(soil, ) avail(rock, ) avail(image, ) at( ) 20 have(soil) 35 have(image) 35 have(rock) 10 at( ) 25 comm(soil) 25 at( ) 35

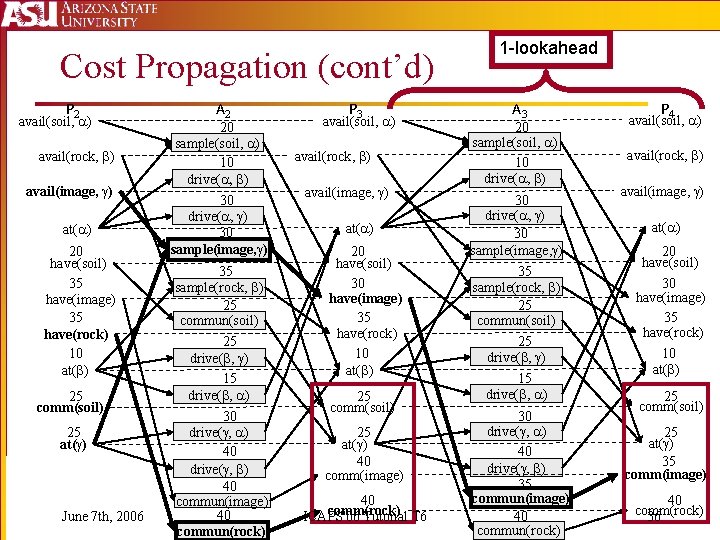
Cost Propagation (cont’d) P 2 avail(soil, ) avail(rock, ) avail(image, ) at( ) 20 have(soil) 35 have(image) 35 have(rock) 10 at( ) 25 comm(soil) 25 at( ) June 7 th, 2006 A 2 20 sample(soil, ) 10 drive( , ) 30 sample(image, ) 35 sample(rock, ) 25 commun(soil) 25 drive( , ) 15 drive( , ) 30 drive( , ) 40 commun(image) 40 commun(rock) P 3 avail(soil, ) avail(rock, ) avail(image, ) at( ) 20 have(soil) 30 have(image) 35 have(rock) 10 at( ) 25 comm(soil) 25 at( ) 40 comm(image) 40 comm(rock) ICAPS'06 Tutorial T 6 1 -lookahead A 3 20 sample(soil, ) 10 drive( , ) 30 sample(image, ) 35 sample(rock, ) 25 commun(soil) 25 drive( , ) 15 drive( , ) 30 drive( , ) 40 drive( , ) 35 commun(image) 40 commun(rock) P 4 avail(soil, ) avail(rock, ) avail(image, ) at( ) 20 have(soil) 30 have(image) 35 have(rock) 10 at( ) 25 comm(soil) 25 at( ) 35 comm(image) 40 comm(rock) 36

Terminating Cost Propagation § Stop when: § goals are reached (no-lookahead) § costs stop changing (∞-lookahead) § k levels after goals are reached (k-lookahead) June 7 th, 2006 ICAPS'06 Tutorial T 6 37

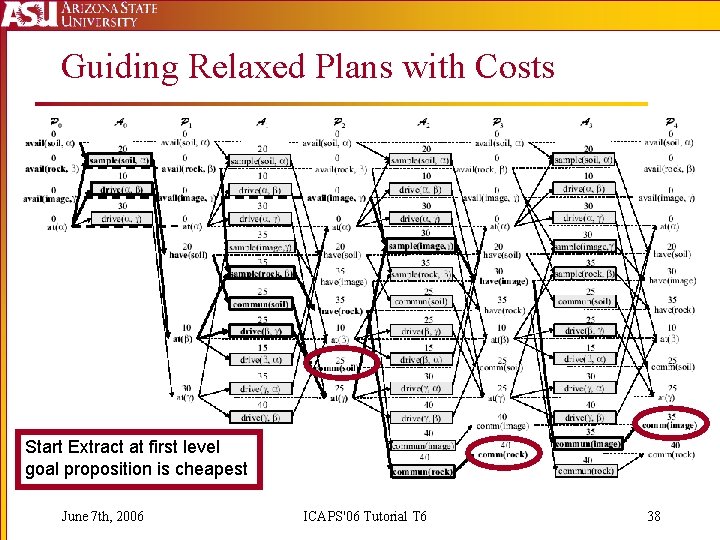
Guiding Relaxed Plans with Costs Start Extract at first level goal proposition is cheapest June 7 th, 2006 ICAPS'06 Tutorial T 6 38

Cost-Based Planning Conclusions § Cost-Functions: § Remove false assumption that level is correlated with cost § Improve planning with non-uniform cost actions § Are cheap to compute (constant overhead) June 7 th, 2006 ICAPS'06 Tutorial T 6 39

Partial Satisfaction (Over-Subscription) Planning June 7 th, 2006 ICAPS'06 Tutorial T 6 40

Partial Satisfaction Planning § Selecting Goal Sets § Estimating goal benefit § Anytime goal set selection § Adjusting for negative interactions between goals June 7 th, 2006 ICAPS'06 Tutorial T 6 41

Partial Satisfaction (Oversubscription) Planning In many real world planning tasks, the agent often has more goals than it has resources to accomplish. Example: Rover Mission Planning (MER) Need automated support for Over-subscription/Partial Satisfaction Planning Actions have execution costs, goals have utilities, and the objective is to find the plan that has the highest net benefit. June 7 th, 2006 ICAPS'06 Tutorial T 6 42

Sapa. PS: Anytime Forward Search • General idea: – Search incrementally while looking for better solutions • Return solutions as they are found… – If we reach a node with h value of 0, then we know we can stop searching (no better solutions can be found) June 7 th, 2006 ICAPS'06 Tutorial T 6 43

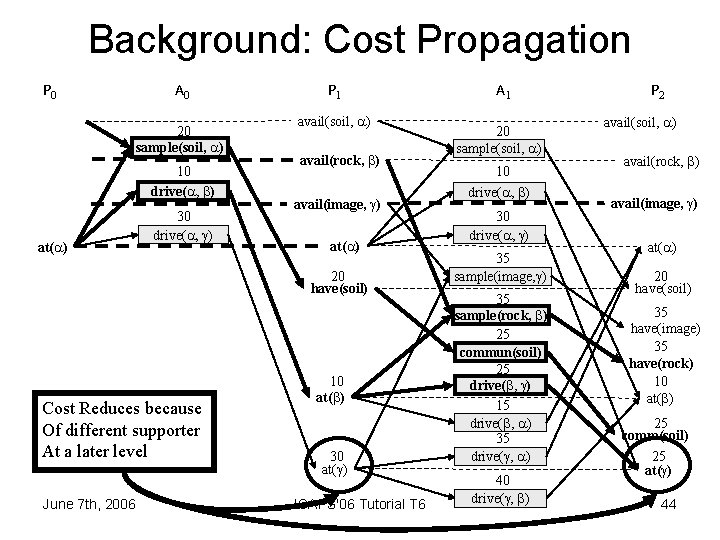
Background: Cost Propagation P 0 A 0 20 sample(soil, ) 10 drive( , ) at( ) 30 drive( , ) P 1 avail(soil, ) avail(rock, ) avail(image, ) at( ) 20 have(soil) Cost Reduces because Of different supporter At a later level June 7 th, 2006 10 at( ) 30 at( ) ICAPS'06 Tutorial T 6 A 1 20 sample(soil, ) 10 drive( , ) 35 sample(image, ) 35 sample(rock, ) 25 commun(soil) 25 drive( , ) 15 drive( , ) 35 drive( , ) 40 drive( , ) P 2 avail(soil, ) avail(rock, ) avail(image, ) at( ) 20 have(soil) 35 have(image) 35 have(rock) 10 at( ) 25 comm(soil) 25 at( ) 44

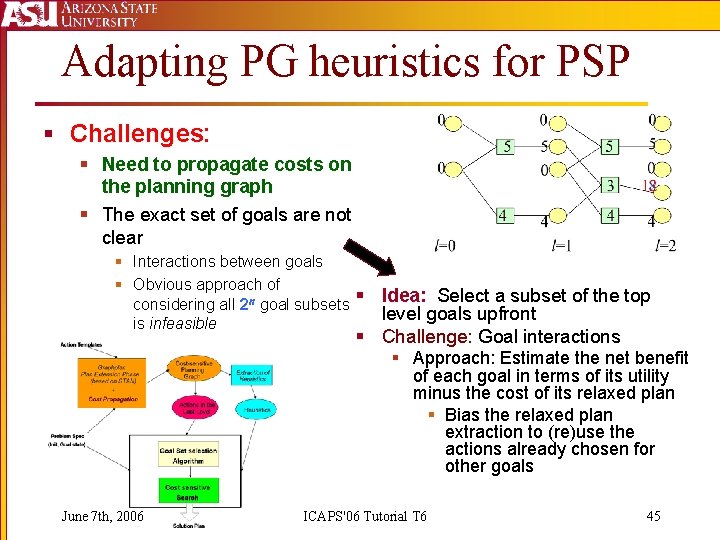
Adapting PG heuristics for PSP § Challenges: § Need to propagate costs on the planning graph § The exact set of goals are not clear § Interactions between goals § Obvious approach of considering all 2 n goal subsets § is infeasible Idea: Select a subset of the top level goals upfront § Challenge: Goal interactions § Approach: Estimate the net benefit of each goal in terms of its utility minus the cost of its relaxed plan § Bias the relaxed plan extraction to (re)use the actions already chosen for other goals June 7 th, 2006 ICAPS'06 Tutorial T 6 45

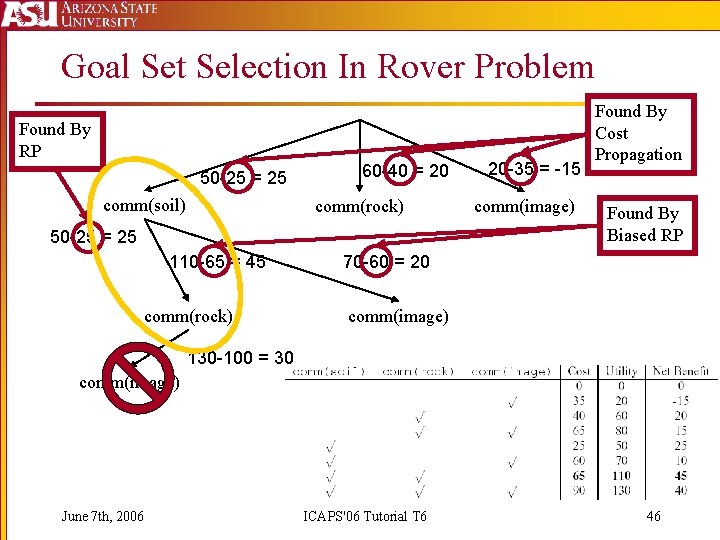
Goal Set Selection In Rover Problem Found By RP 50 -25 = 25 comm(soil) 60 -40 = 20 comm(rock) 50 -25 = 25 110 -65 = 45 comm(rock) 20 -35 = -15 comm(image) Found By Cost Propagation Found By Biased RP 70 -60 = 20 comm(image) 130 -100 = 30 comm(image) June 7 th, 2006 ICAPS'06 Tutorial T 6 46

SAPAPS (anytime goal selection) § A* Progression search § g-value: net-benefit of plan so far § h-value: relaxed plan estimate of best goal set § Relaxed plan found for all goals § Iterative goal removal, until net benefit does not increase § Returns plans with increasing g-values. June 7 th, 2006 ICAPS'06 Tutorial T 6 47

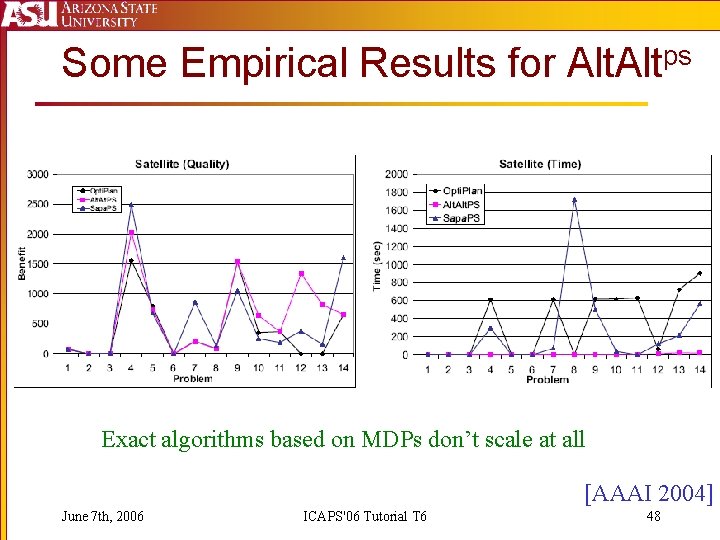
Some Empirical Results for Altps Exact algorithms based on MDPs don’t scale at all [AAAI 2004] June 7 th, 2006 ICAPS'06 Tutorial T 6 48

Adjusting for Negative Interactions (Alt. Wlt) § Problem: § What if the apriori goal set is not achievable because of negative interactions? § What if greedy algorithm gets bad local optimum? § Solution: § Do not consider mutex goals § Add penalty for goals whose relaxed plan has mutexes. § Use interaction factor to adjust cost, similar to adjusted sum heuristic § maxg 1, g 2 2 G {lev(g 1, g 2) – max(lev(g 1), lev(g 2)) } § Find Best Goal set for each goal June 7 th, 2006 ICAPS'06 Tutorial T 6 49

Goal Utility Dependencies BAD GOOD Cost: 50 Utility: 0 Cost: 100 Utility: 500 High-res photo utility: 150 Soil sample utility: 100 Low-res photo utility: 100 June 7 th, 2006 T 6 goals: Remove 80 Both goals: Additional. ICAPS'06 200 Tutorial Both 50

Partial Satisfaction Planning (PSP) Agent has more goals than it has resources to accomplish Objective: Find a plan with highest net benefit – Goals have utility – Actions have cost (i. e. maximize (utility – cost)) Challenges: Unclear as to which goals to achieve Interactions exist between goals June 7 th, 2006 ICAPS'06 Tutorial T 6 51

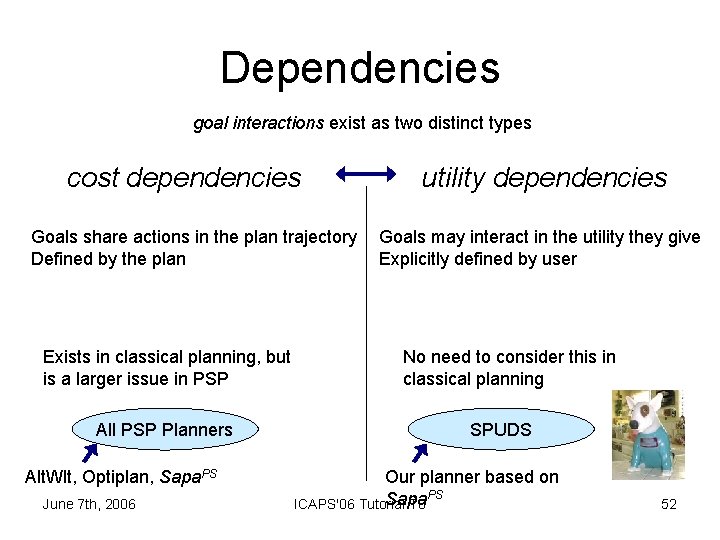
Dependencies goal interactions exist as two distinct types cost dependencies Goals share actions in the plan trajectory Defined by the plan Exists in classical planning, but is a larger issue in PSP All PSP Planners Alt. Wlt, Optiplan, Sapa. PS June 7 th, 2006 utility dependencies Goals may interact in the utility they give Explicitly defined by user No need to consider this in classical planning SPUDS Our planner based on PS Sapa ICAPS'06 Tutorial T 6 52

Defining Goal Dependencies Follow the General Additive Independence (GAI) Model (Bacchus & Grove) Goals listed with additive utility Goal set Utility over set June 7 th, 2006 ICAPS'06 Tutorial T 6 53 Bacchus, F. , and Grove, A. 1995. Graphical models for preference and utility. In Proc. of UAI-95.

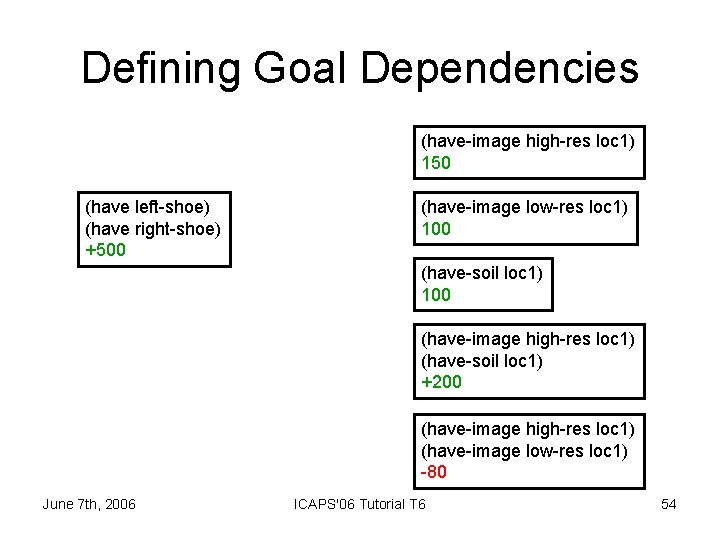
Defining Goal Dependencies (have-image high-res loc 1) 150 (have left-shoe) (have right-shoe) +500 (have-image low-res loc 1) 100 (have-soil loc 1) 100 (have-image high-res loc 1) (have-soil loc 1) +200 (have-image high-res loc 1) (have-image low-res loc 1) -80 June 7 th, 2006 ICAPS'06 Tutorial T 6 54

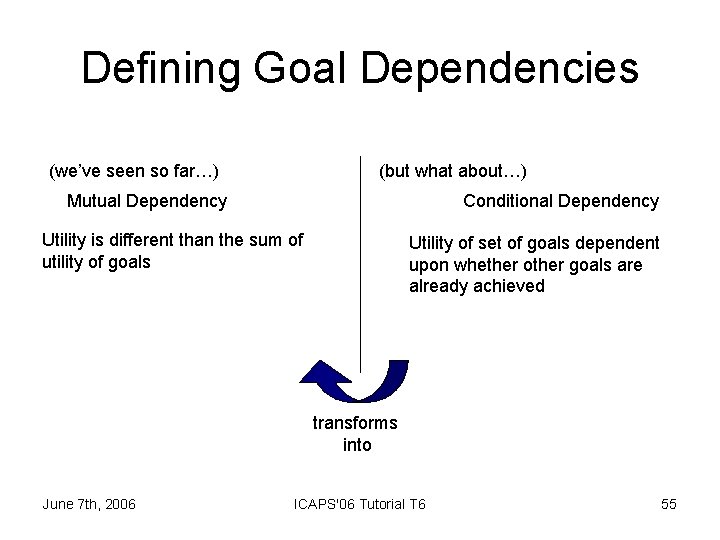
Defining Goal Dependencies (we’ve seen so far…) (but what about…) Mutual Dependency Conditional Dependency Utility is different than the sum of utility of goals Utility of set of goals dependent upon whether other goals are already achieved transforms into June 7 th, 2006 ICAPS'06 Tutorial T 6 55

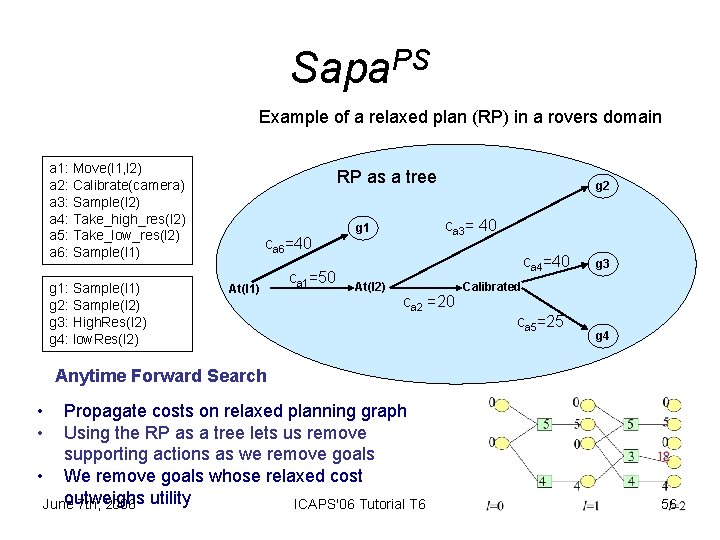
Sapa. PS Example of a relaxed plan (RP) in a rovers domain a 1: Move(l 1, l 2) a 2: Calibrate(camera) a 3: Sample(l 2) a 4: Take_high_res(l 2) a 5: Take_low_res(l 2) a 6: Sample(l 1) g 1: Sample(l 1) g 2: Sample(l 2) g 3: High. Res(l 2) g 4: low. Res(l 2) RP as a tree ca 6=40 At(l 1) ca 1=50 g 2 ca 3= 40 g 1 ca 4=40 At(l 2) ca 2 =20 g 3 Calibrated ca 5=25 g 4 Anytime Forward Search • • Propagate costs on relaxed planning graph Using the RP as a tree lets us remove supporting actions as we remove goals • We remove goals whose relaxed cost outweighs June 7 th, 2006 utility ICAPS'06 Tutorial T 6 56

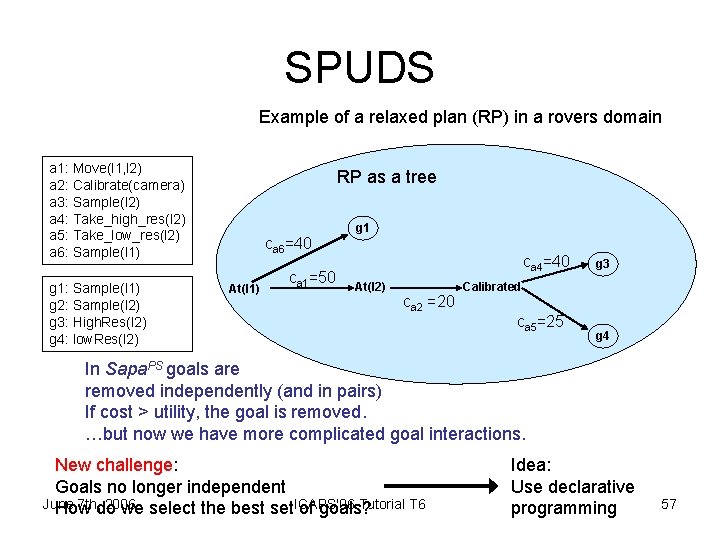
SPUDS Example of a relaxed plan (RP) in a rovers domain a 1: Move(l 1, l 2) a 2: Calibrate(camera) a 3: Sample(l 2) a 4: Take_high_res(l 2) a 5: Take_low_res(l 2) a 6: Sample(l 1) g 1: Sample(l 1) g 2: Sample(l 2) g 3: High. Res(l 2) g 4: low. Res(l 2) RP as a tree ca 6=40 At(l 1) ca 1=50 g 1 ca 4=40 At(l 2) ca 2 =20 g 3 Calibrated ca 5=25 g 4 In Sapa. PS goals are removed independently (and in pairs) If cost > utility, the goal is removed. …but now we have more complicated goal interactions. New challenge: Goals no longer independent June 7 th, do 2006 Tutorial T 6 How we select the best set. ICAPS'06 of goals? Idea: Use declarative programming 57

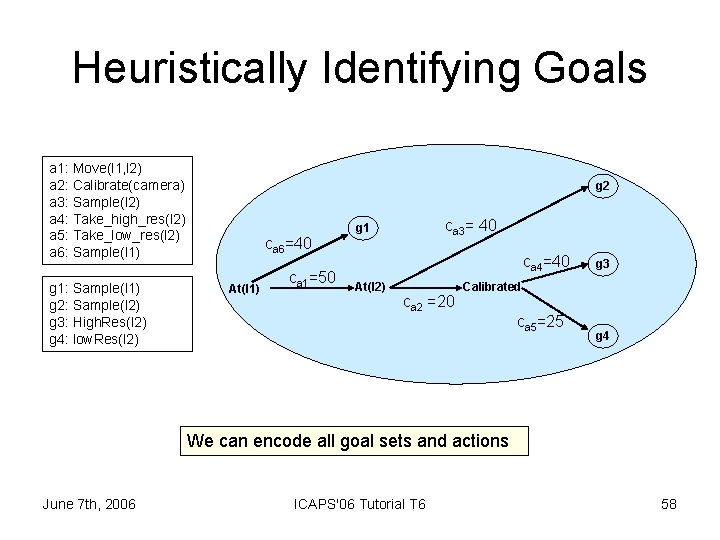
Heuristically Identifying Goals a 1: Move(l 1, l 2) a 2: Calibrate(camera) a 3: Sample(l 2) a 4: Take_high_res(l 2) a 5: Take_low_res(l 2) a 6: Sample(l 1) g 1: Sample(l 1) g 2: Sample(l 2) g 3: High. Res(l 2) g 4: low. Res(l 2) g 2 ca 6=40 At(l 1) ca 1=50 ca 3= 40 g 1 ca 4=40 At(l 2) ca 2 =20 g 3 Calibrated ca 5=25 g 4 We can encode all goal sets and actions June 7 th, 2006 ICAPS'06 Tutorial T 6 58

Heuristically Identifying Goals We encode the relaxed plan Binary Variables goal utility dependencies goals actions Constraints Select actions for goals Select goals in dependency Objective function: where June 7 th, 2006 gives the utility given by the goal set , cost of gives all goals action is involved in reaching ICAPS'06 Tutorial T 6 and 59

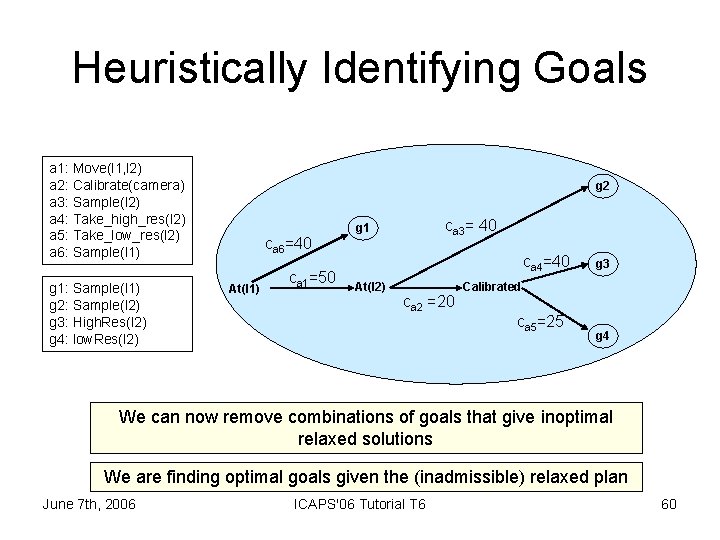
Heuristically Identifying Goals a 1: Move(l 1, l 2) a 2: Calibrate(camera) a 3: Sample(l 2) a 4: Take_high_res(l 2) a 5: Take_low_res(l 2) a 6: Sample(l 1) g 1: Sample(l 1) g 2: Sample(l 2) g 3: High. Res(l 2) g 4: low. Res(l 2) g 2 ca 6=40 At(l 1) ca 1=50 ca 3= 40 g 1 ca 4=40 At(l 2) ca 2 =20 g 3 Calibrated ca 5=25 g 4 We can now remove combinations of goals that give inoptimal relaxed solutions We are finding optimal goals given the (inadmissible) relaxed plan June 7 th, 2006 ICAPS'06 Tutorial T 6 60

Experimental Domains • Goal utilities randomly generated • Goals “hard” or “soft” • Goal dependencies randomly generated §number of dependencies §their size §the set of goals involved §their utility value • Upper bound on the number of dependencies is 3 x number of goals • Compared SPUDS to Sapa. PS §Sapa. PS modified to calculate goal utility dependencies at each state June 7 th, 2006 Domain Cost Zeno. Travel Money spent Satellite Energy spent ICAPS'06 Tutorial T 6 61

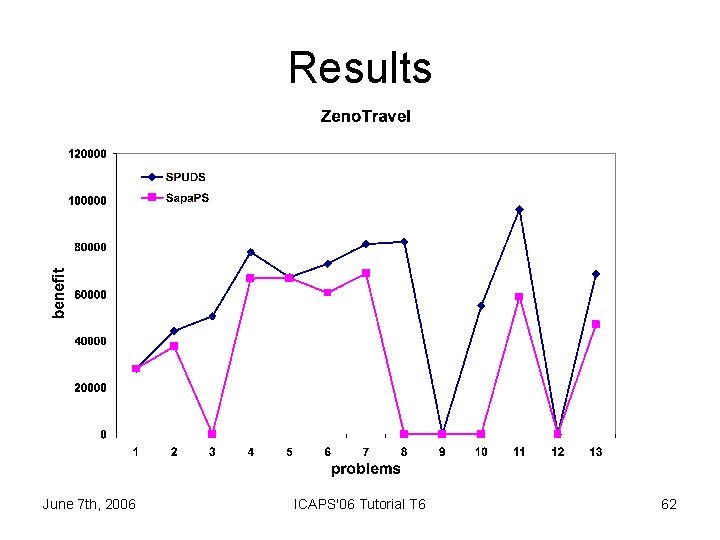
Results June 7 th, 2006 ICAPS'06 Tutorial T 6 62

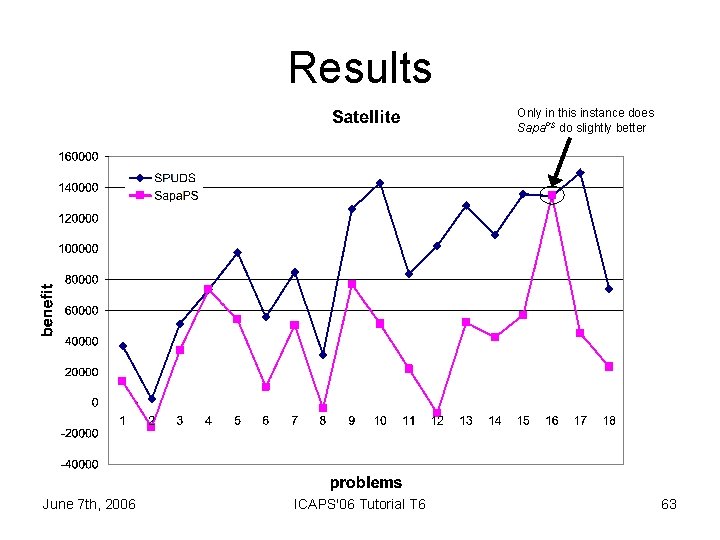
Results Only in this instance does Sapa. PS do slightly better June 7 th, 2006 ICAPS'06 Tutorial T 6 63

Results Our experiments show that the ILP encoding takes upwards of 200 x more time Sapa. PS procedure per node. is still doing better. Ourthan newthen heuristic is better informed about Yet costitdependencies PS Sapa heuristic lacks the ability to take utility dependency into account. Why? between goals. Obvious A little less obvious June 7 th, 2006 ICAPS'06 Tutorial T 6 64

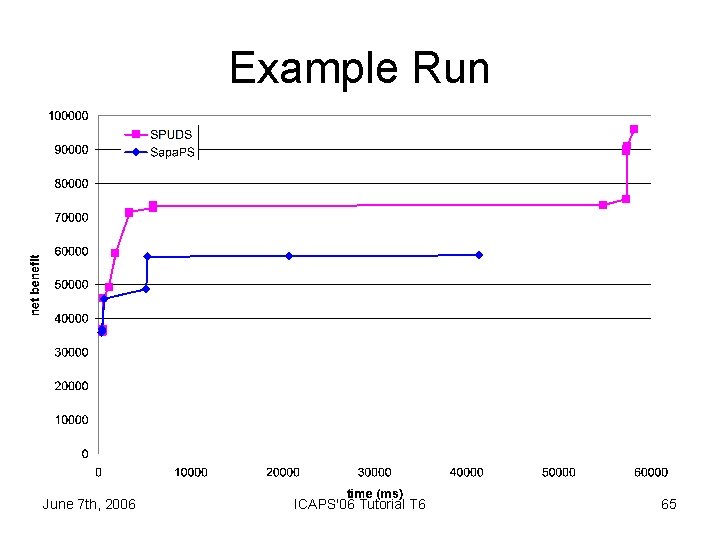
Example Run June 7 th, 2006 ICAPS'06 Tutorial T 6 65

Summary • Goal utility dependency in GAI framework • Choosing goals at each search node • ILP-based heuristic enhances search guidance – cost dependencies – utility dependencies June 7 th, 2006 ICAPS'06 Tutorial T 6 66

Future Work • Comparing with other planners (IP) – Results promising so far (better quality in less time) • Include qualitative preference model as in Pref. Plan (Brafman & Chernyavsky) • Take into account residual cost as in Alt. Wlt (Sanchez & Kambhampati) • Extend into PDDL 3 preference model June 7 th, 2006 ICAPS'06 Tutorial T 6 67

Questions June 7 th, 2006 ICAPS'06 Tutorial T 6 68

The Problem with Plangraphs [Smith, ICAPS 04] 0 0 5 1 5 0 5 1 0 2 5 2 1 7 5 3 1 7 5 0 5 2 0 3 3 1 0 Assume independence between objectives For rover: all estimates from starting location June 7 th, 2006 ICAPS'06 Tutorial T 6 69

Approach – Construct orienteering problem – Solve it – Use as search guidance June 7 th, 2006 ICAPS'06 Tutorial T 6 70

Orienteering Problem TSP variant – Given: network of cities rewards in various cities finite amount of gas – Objective: collect as much reward as possible before running out of gas June 7 th, 2006 ICAPS'06 Tutorial T 6 71

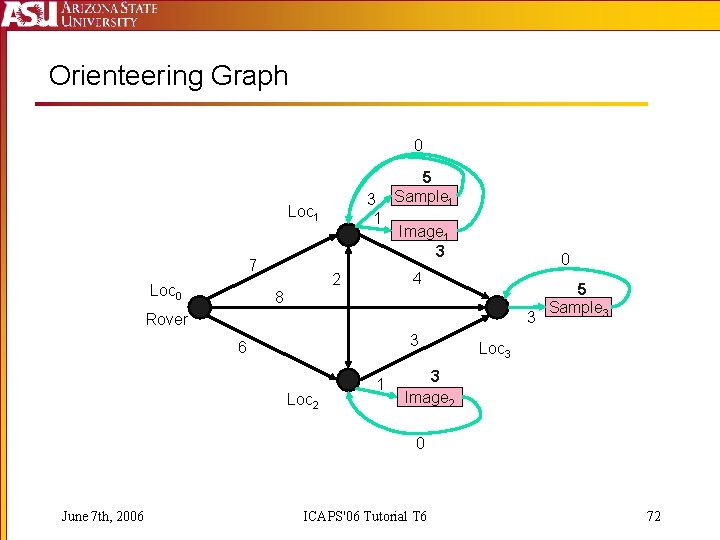
Orienteering Graph 0 3 1 Loc 1 7 Loc 0 5 Sample 1 Image 1 3 0 4 2 8 3 Rover 3 6 Loc 2 1 5 Sample 3 Loc 3 3 Image 2 0 June 7 th, 2006 ICAPS'06 Tutorial T 6 72

The Big Question: How do we determine which propositions go in the orienteering graph? Propositions that: are changed in achieving one goal impact the cost of another goal Sensitivity analysis June 7 th, 2006 ICAPS'06 Tutorial T 6 73

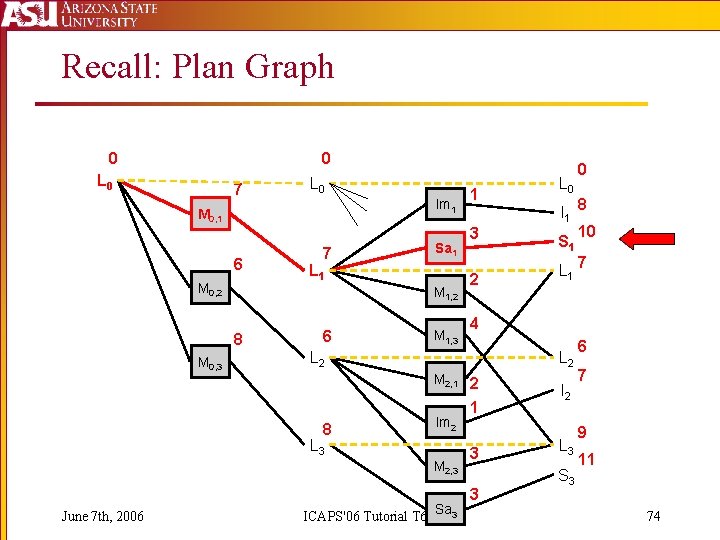
Recall: Plan Graph 0 0 L 0 7 L 0 Im 1 M 0, 1 6 M 0, 2 Sa 1 L 1 M 1, 2 8 M 0, 3 7 6 M 1, 3 3 2 L 0 I 1 S 1 L 2 M 2, 1 2 Im 2 L 3 M 2, 3 ICAPS'06 Tutorial T 6 Sa 3 8 10 7 4 L 2 8 June 7 th, 2006 1 0 1 3 3 I 2 L 3 S 3 6 7 9 11 74

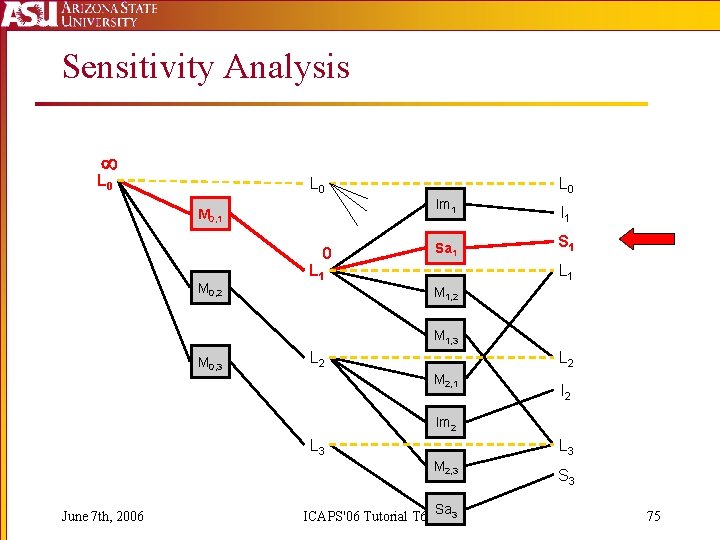
Sensitivity Analysis L 0 Im 1 M 0, 1 0 M 0, 2 L 0 Sa 1 L 1 I 1 S 1 L 1 M 1, 2 M 1, 3 M 0, 3 L 2 M 2, 1 I 2 Im 2 L 3 M 2, 3 June 7 th, 2006 ICAPS'06 Tutorial T 6 Sa 3 S 3 75

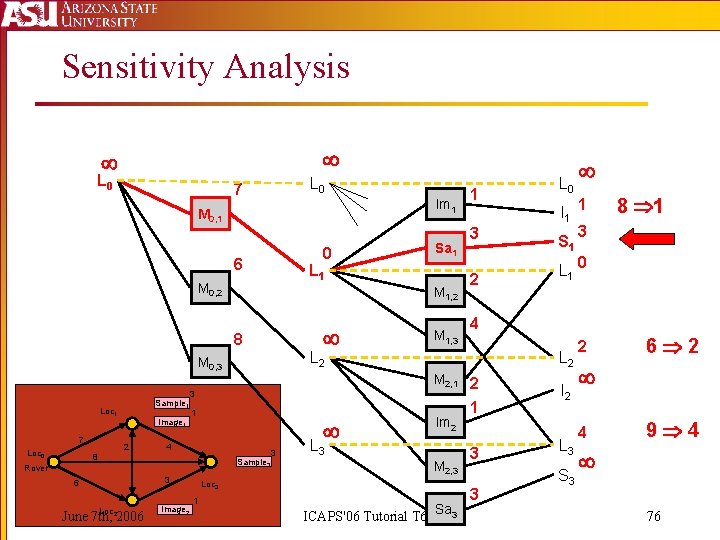
Sensitivity Analysis L 0 7 Im 1 M 0, 1 0 6 L 1 M 0, 2 M 1, 2 8 Sample 1 7 Loc 0 Image 1 2 8 1 4 Sample 3 3 6 Loc June 7 th, 22006 Image 2 3 I 1 S 1 L 1 Im 2 L 3 M 2, 3 ICAPS'06 Tutorial T 6 Sa 3 1 8 1 3 0 4 L 2 Loc 3 1 2 M 2, 1 2 3 Rover M 1, 3 3 L 2 M 0, 3 Loc 1 Sa 1 1 L 0 1 3 3 I 2 L 3 S 3 2 6 2 4 9 4 76

Basis Set Algorithm For each goal: Construct a relaxed plan For each net effect of relaxed plan: Reset costs in PG Set cost of net effect to 0 Set cost of mutex initial conditions to Compute revised cost estimates If significantly different, add net effect to basis set June 7 th, 2006 ICAPS'06 Tutorial T 6 77

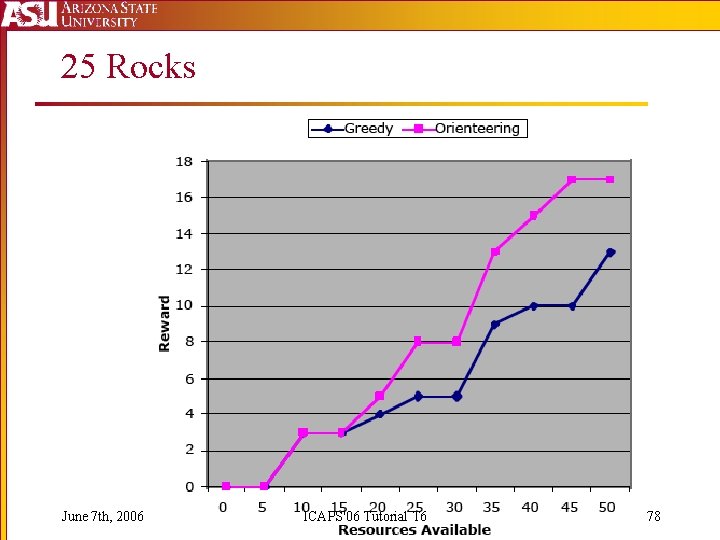
25 Rocks June 7 th, 2006 ICAPS'06 Tutorial T 6 78

PSP Conclusions § Goal Set Selection § Apriori for Regression Search § Anytime for Progression Search § Both types of search use greedy goal insertion/removal to optimize net-benefit of relaxed plans § Orienteering Problem § Interactions between goals apparent in OP § Use solution to OP as heuristic § Planning Graphs help define OP June 7 th, 2006 ICAPS'06 Tutorial T 6 79

Planning with Resources June 7 th, 2006 ICAPS'06 Tutorial T 6 80

Planning with Resources § Propagating Resource Intervals § Relaxed Plans § Handling resource subgoals June 7 th, 2006 ICAPS'06 Tutorial T 6 81

Rover with power Resource Usage, Same as costs for This example June 7 th, 2006 ICAPS'06 Tutorial T 6 82

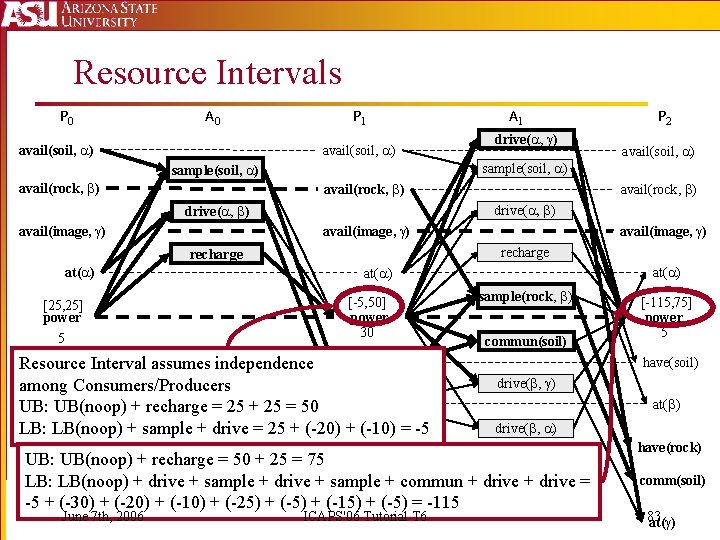
Resource Intervals P 0 A 0 avail(soil, ) P 1 avail(soil, ) avail(rock, ) 5 avail(image, ) recharge [25, 25] power avail(rock, ) avail(image, ) at( ) [-5, 50] power 30 Resource Interval assumes independence have(soil) among Consumers/Producers UB: UB(noop) + recharge = 25 + 25 = 50 at( ) LB: LB(noop) + sample + drive = 25 + (-20) + (-10) = -5 sample(rock, ) commun(soil) ICAPS'06 Tutorial T 6 [-115, 75] power 5 have(soil) drive( , ) at( ) drive( , ) UB: UB(noop) + recharge = 50 + 25 = 75 LB: LB(noop) + drive + sample + commun + drive = -5 + (-30) + (-20) + (-10) + (-25) + (-15) + (-5) = -115 June 7 th, 2006 avail(soil, ) drive( , ) at( ) drive( , ) P 2 sample(soil, ) avail(rock, ) A 1 have(rock) comm(soil) 83 at( )

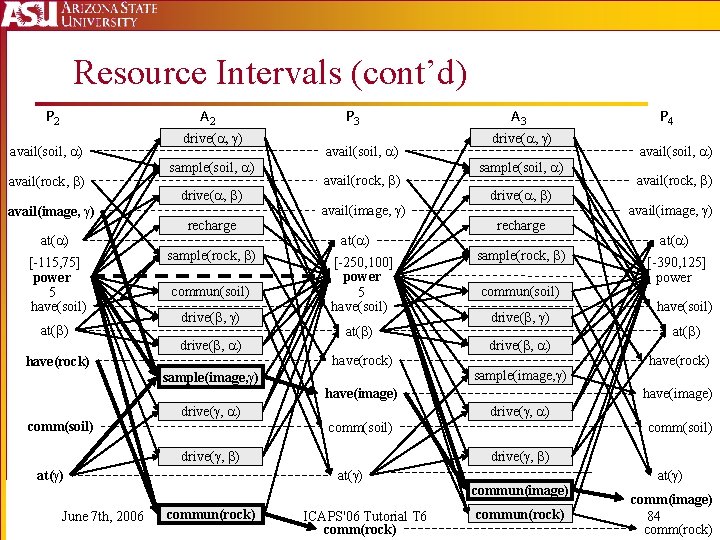
Resource Intervals (cont’d) P 2 A 2 avail(soil, ) avail(rock, ) avail(image, ) at( ) [-115, 75] power 5 have(soil) at( ) have(rock) drive( , ) sample(soil, ) drive( , ) recharge sample(rock, ) commun(soil) drive( , ) P 3 avail(soil, ) avail(rock, ) avail(image, ) at( ) [-250, 100] power 5 have(soil) at( ) have(rock) sample(image, ) A 3 drive( , ) sample(soil, ) drive( , ) recharge sample(rock, ) commun(soil) drive( , ) sample(image, ) have(image) comm(soil) drive( , ) avail(image, ) at( ) [-390, 125] power have(soil) at( ) have(rock) comm(soil) drive( , ) at( ) commun(rock) avail(rock, ) drive( , ) June 7 th, 2006 avail(soil, ) have(image) comm(soil) at( ) P 4 ICAPS'06 Tutorial T 6 comm(rock) commun(image) commun(rock) at( ) comm(image) 84 comm(rock)

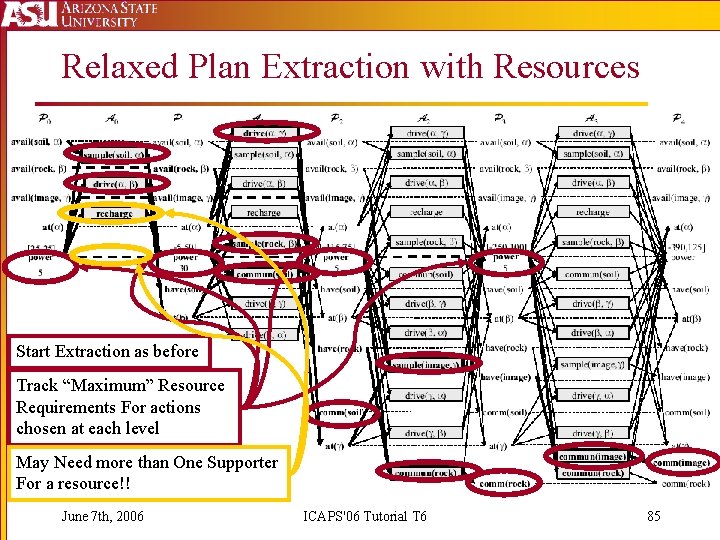
Relaxed Plan Extraction with Resources Start Extraction as before Track “Maximum” Resource Requirements For actions chosen at each level May Need more than One Supporter For a resource!! June 7 th, 2006 ICAPS'06 Tutorial T 6 85

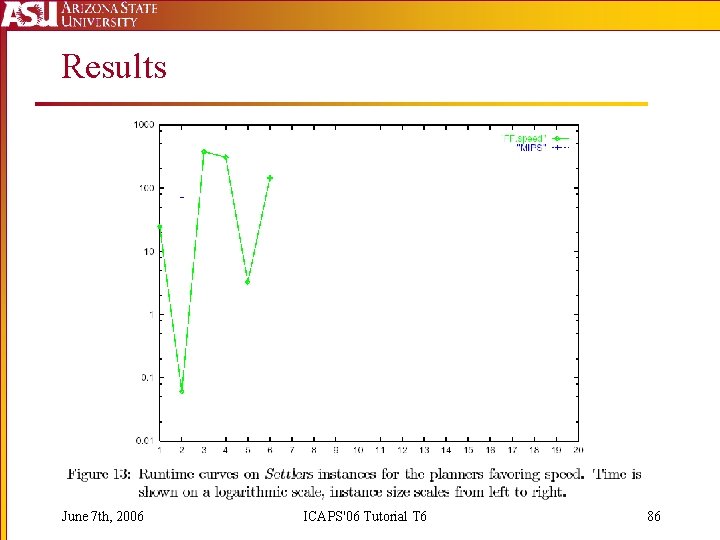
Results June 7 th, 2006 ICAPS'06 Tutorial T 6 86

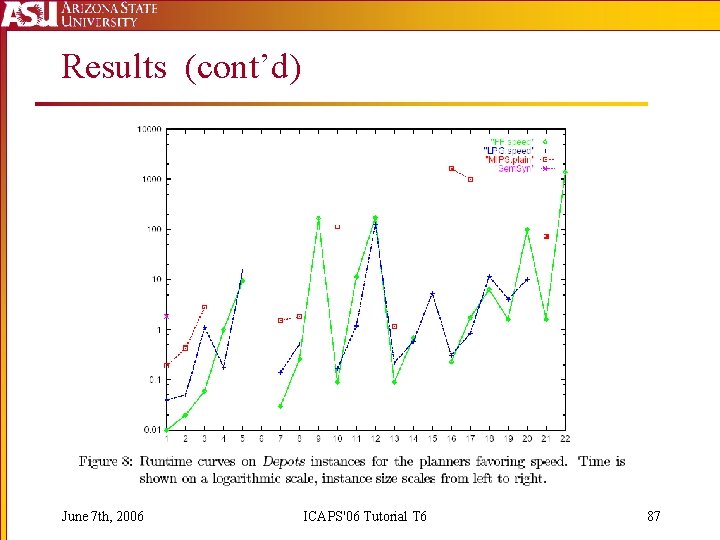
Results (cont’d) June 7 th, 2006 ICAPS'06 Tutorial T 6 87

Planning With Resources Conclusion § Resource Intervals allow us to be optimistic about reachable values § Upper/Lower bounds can get large § Relaxed Plans may require multiple supporters for subgoals § Negative Interactions are much harder to capture June 7 th, 2006 ICAPS'06 Tutorial T 6 88

Temporal Planning June 7 th, 2006 ICAPS'06 Tutorial T 6 89

Temporal Planning § Temporal Planning Graph § From Levels to Time Points § Delayed Effects § Estimating Makespan § Relaxed Plan Extraction June 7 th, 2006 ICAPS'06 Tutorial T 6 90

Rover with Durative Actions June 7 th, 2006 ICAPS'06 Tutorial T 6 91

SAPA [ECP 2001; AIPS 2002; ICAPS 2003; JAIR 2003] June 7 th, 2006 ICAPS'06 Tutorial T 6 92

Search through time-stamped states § Goal Satisfaction: S=(P, M, , Q, t) G if <pi, ti> G either: § <pi, tj> P, tj < ti and no event in Q deletes pi. § e Q that adds pi at time te < ti. § Action Application: Action A is applicable in S if: § All instantaneous preconditions of A are satisfied by P and M. § A’s effects do not interfere with and Q. § No event in Q interferes with persistent preconditions of A. § A does not lead to concurrent resource change § When A is applied to S: § P is updated according to A’s instantaneous effects. § Persistent preconditions of A are put in § Delayed effects of A are put in Q. June 7 th, 2006 ICAPS'06 Tutorial T 6 93

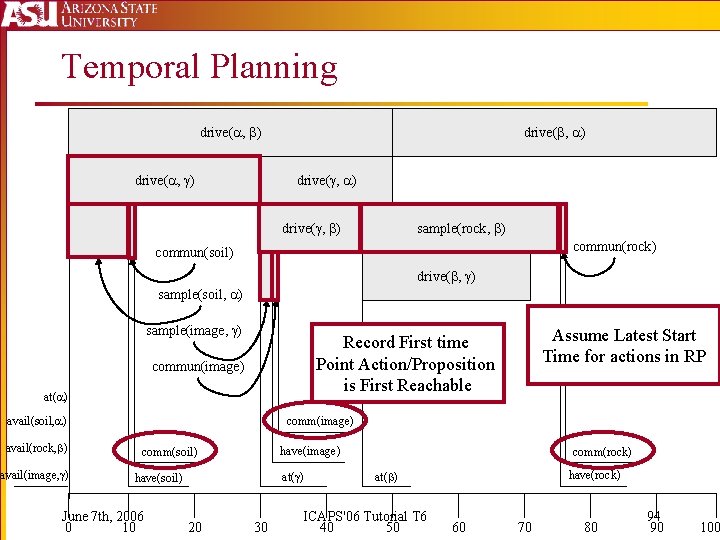
Temporal Planning drive( , ) drive( , ) sample(rock, ) commun(rock) commun(soil) drive( , ) sample(soil, ) sample(image, ) commun(image) at( ) avail(soil, ) avail(rock, ) avail(image, ) Assume Latest Start Time for actions in RP Record First time Point Action/Proposition is First Reachable comm(image) have(image) comm(soil) at( ) have(soil) June 7 th, 2006 0 10 20 30 comm(rock) have(rock) at( ) ICAPS'06 Tutorial T 6 40 50 60 70 80 94 90 100

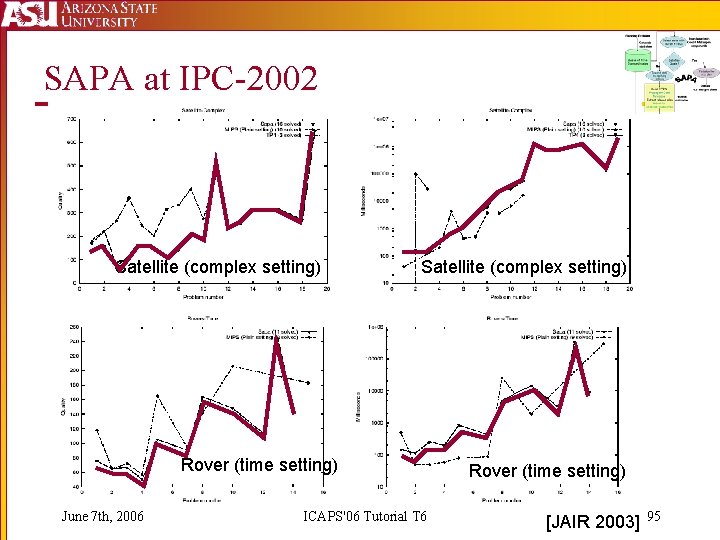
SAPA at IPC-2002 Satellite (complex setting) Rover (time setting) June 7 th, 2006 ICAPS'06 Tutorial T 6 Rover (time setting) [JAIR 2003] 95

Temporal Planning Conclusion § Levels become Time Points § Makespan and plan length/cost are different objectives § Set-Level heuristic measures makespan § Relaxed Plans measure makespan and plan cost June 7 th, 2006 ICAPS'06 Tutorial T 6 96

Non-Deterministic Planning June 7 th, 2006 ICAPS'06 Tutorial T 6 97

Non-Deterministic Planning § § Belief State Distance Multiple Planning Graphs Labelled Uncertainty Graph Implicit Belief states and the CFF heuristic June 7 th, 2006 ICAPS'06 Tutorial T 6 98

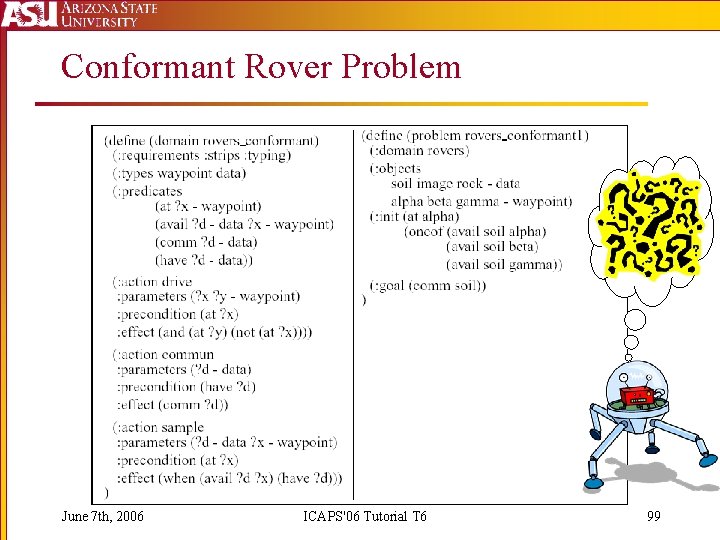
Conformant Rover Problem June 7 th, 2006 ICAPS'06 Tutorial T 6 99

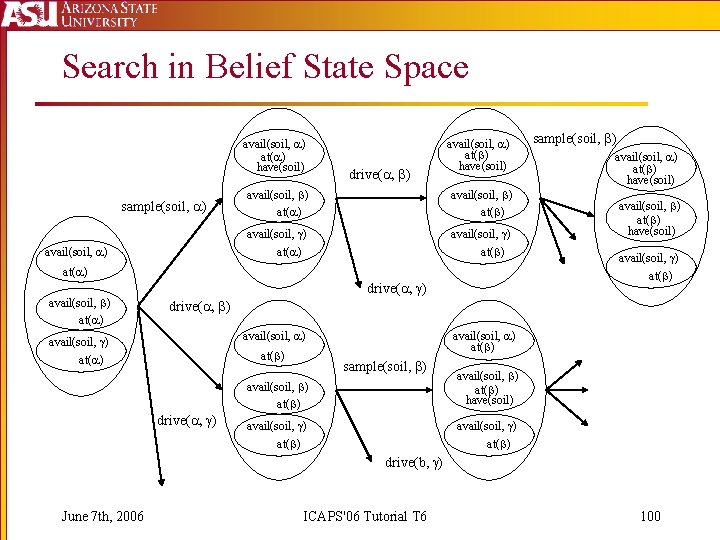
Search in Belief State Space avail(soil, ) at( ) have(soil) sample(soil, ) avail(soil, ) drive( , ) avail(soil, ) at( ) have(soil) avail(soil, ) at( ) at( ) avail(soil, ) at( ) sample(soil, ) avail(soil, ) at( ) have(soil) avail(soil, ) at( ) drive( , ) avail(soil, ) at( ) sample(soil, ) avail(soil, ) at( ) have(soil) avail(soil, ) at( ) drive(b, ) June 7 th, 2006 ICAPS'06 Tutorial T 6 100

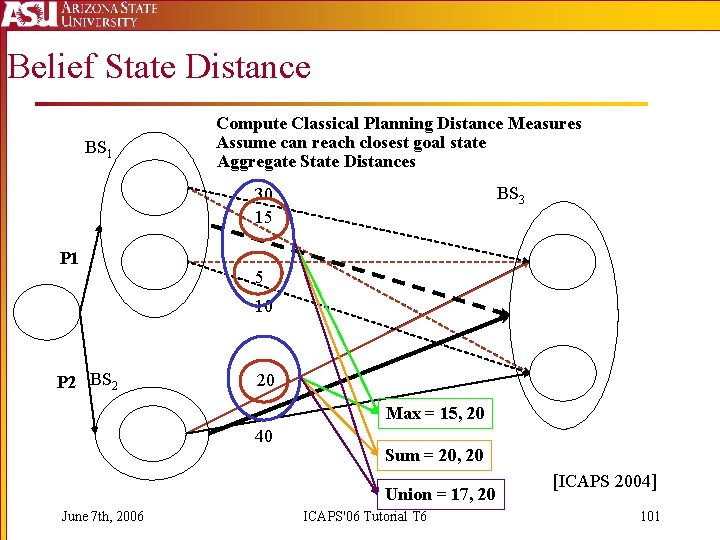
Belief State Distance BS 1 Compute Classical Planning Distance Measures Assume can reach closest goal state Aggregate State Distances BS 3 30 15 P 1 5 10 P 2 BS 2 20 Max = 15, 20 40 Sum = 20, 20 Union = 17, 20 June 7 th, 2006 ICAPS'06 Tutorial T 6 [ICAPS 2004] 101

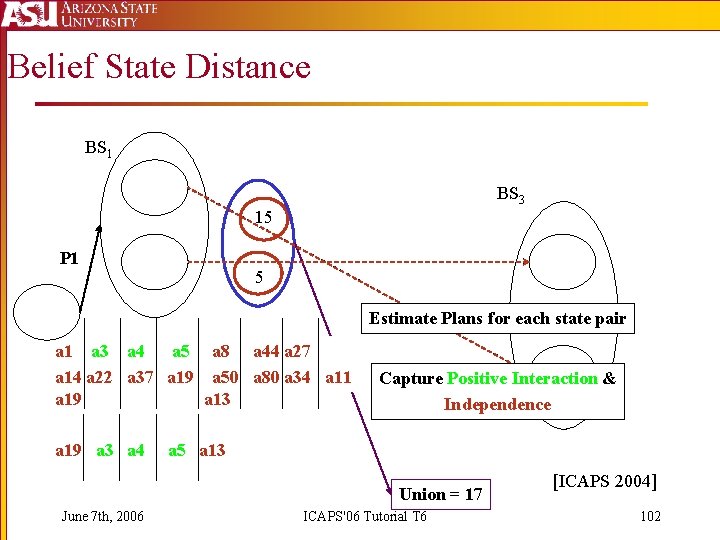
Belief State Distance BS 1 BS 3 15 P 1 5 Estimate Plans for each state pair a 1 a 3 a 4 a 5 a 8 a 44 a 27 a 14 a 22 a 37 a 19 a 50 a 80 a 34 a 11 a 19 a 13 a 19 a 3 a 4 Capture Positive Interaction & Independence a 5 a 13 Union = 17 June 7 th, 2006 ICAPS'06 Tutorial T 6 [ICAPS 2004] 102

State Distance Aggregations Over-estimates [Bryce et. al, 2005] Max Sum Union Just Right Under-estimates June 7 th, 2006 ICAPS'06 Tutorial T 6 103

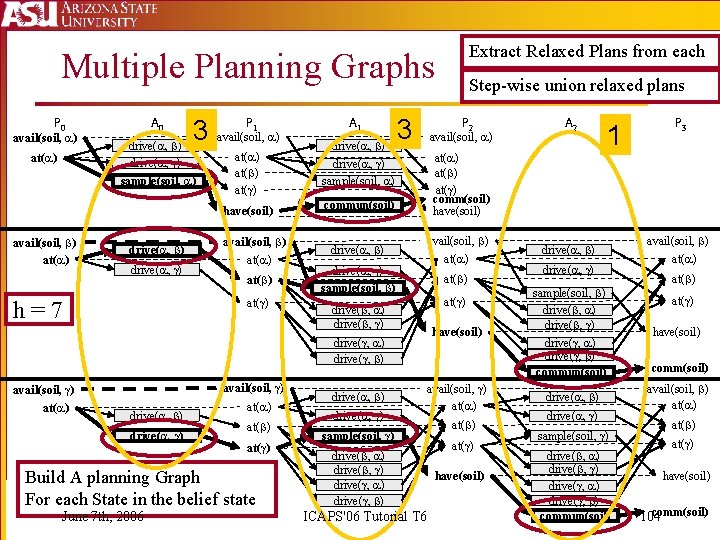
Extract Relaxed Plans from each Multiple Planning Graphs P 0 avail(soil, ) at( ) A 0 3 drive( , ) sample(soil, ) drive( , ) P 1 avail(soil, ) drive( , ) at( ) drive( , ) sample(soil, ) have(soil) commun(soil) avail(soil, ) at( ) h=7 A 1 drive( , ) 3 P 2 avail(soil, ) at( ) drive( , ) sample(soil, ) at( ) drive( , ) at( ) Build A planning Graph For each State in the belief state June 7 th, 2006 drive( , ) A 2 1 P 3 at( ) comm(soil) have(soil) drive( , ) avail(soil, ) Step-wise union relaxed plans avail(soil, ) at( ) sample(soil, ) drive( , ) ICAPS'06 Tutorial T 6 at( ) have(soil) drive( , ) sample(soil, ) drive( , ) drive( , ) commun(soil) avail(soil, ) at( ) at( ) have(soil) comm(soil) 104

Labelled Uncertainty Graph P 0 A 0 P 1 A 1 P 2 avail(soil, ) Action labels are the Conjunction (intersection) of their Precondition labels A 2 P 3 avail(soil, ) avail(soil, ) avail(soil, ) sample(soil, ) at( ) Æ ( avail(soil, ) Ç avail(soil, ) )Æ : at( ) Æ … at( ) drive( , ) Labels correspond To sets of states, and Are represented as Propositional formulas June 7 th, 2006 have(soil) sample(soil, ) at( ) sample(soil, ) comm(soil) sample(soil, ) commun(soil) drive( , ) have(soil) comm(soil) at( ) drive( , ) at( ) drive( , are ) the Effect labels Disjunction (union) drive( , ) of ICAPS'06 supporter. Tutorial labels T 6 drive( , ) drive( , Stop when )goal is Labeled drive( , with ) every state 105 drive( , ) at( )

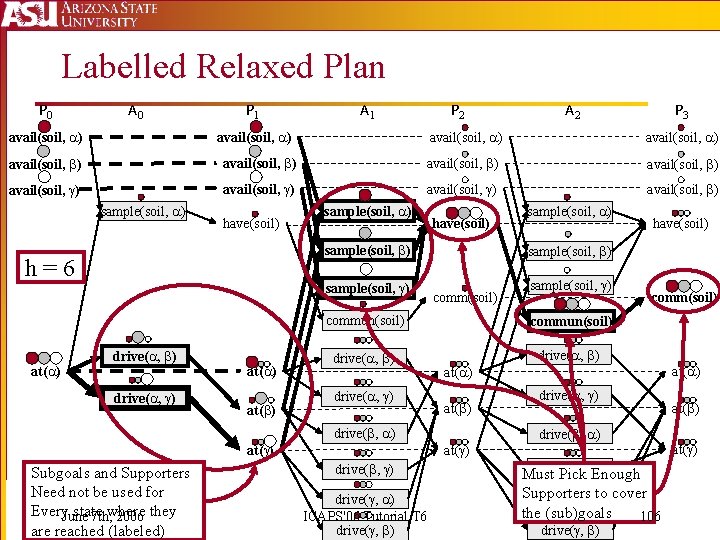
Labelled Relaxed Plan P 0 A 0 P 1 A 1 P 2 avail(soil, ) A 2 P 3 avail(soil, ) avail(soil, ) avail(soil, ) sample(soil, ) have(soil) sample(soil, ) h=6 at( ) sample(soil, ) drive( , ) at( ) comm(soil) sample(soil, ) commun(soil) drive( , ) have(soil) sample(soil, ) comm(soil) at( ) drive( , ) at( ) Subgoals and Supporters Need not be used for Every. June state 7 th, where 2006 they are reached (labeled) sample(soil, ) drive( , ) ICAPS'06 Tutorial T 6 drive( , ) drive( , Must Pick )Enough Supporters drive( , )to cover the (sub)goals 106 drive( , ) at( )

Comparison of Planning Graph Types [JAIR, 2006] LUG saves Time Sampling more worlds, Increases cost of MG Sampling more worlds, Improves effectiveness of LUG June 7 th, 2006 ICAPS'06 Tutorial T 6 107

State Agnostic Planning Graphs (SAG) § LUG represents multiple explicit planning graphs § SAG uses LUG to represent a planning graph for every state § The SAG is built once per search episode and we can use it for relaxed plans for every search node, instead of building a LUG at every node § Extract relaxed plans from SAG by ignoring planning graph components not labeled by states in our search node. June 7 th, 2006 ICAPS'06 Tutorial T 6 108

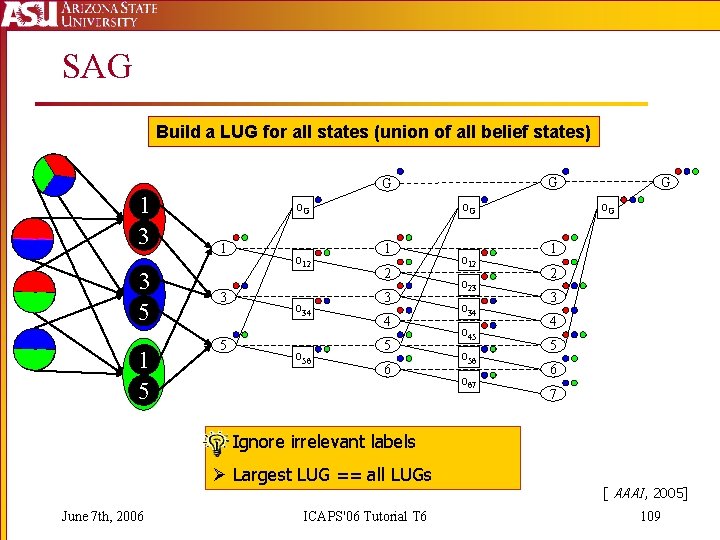
SAG Build a LUG for all states (union of all belief states) G G 1 3 3 5 1 5 o. G 1 3 5 o 12 o 34 o 56 o. G 1 2 3 4 5 6 o 12 o 23 o 34 o 45 o 56 o 67 G o. G 1 2 3 4 5 6 7 § Ignore irrelevant labels Ø Largest LUG == all LUGs June 7 th, 2006 ICAPS'06 Tutorial T 6 [ AAAI, 2005] 109

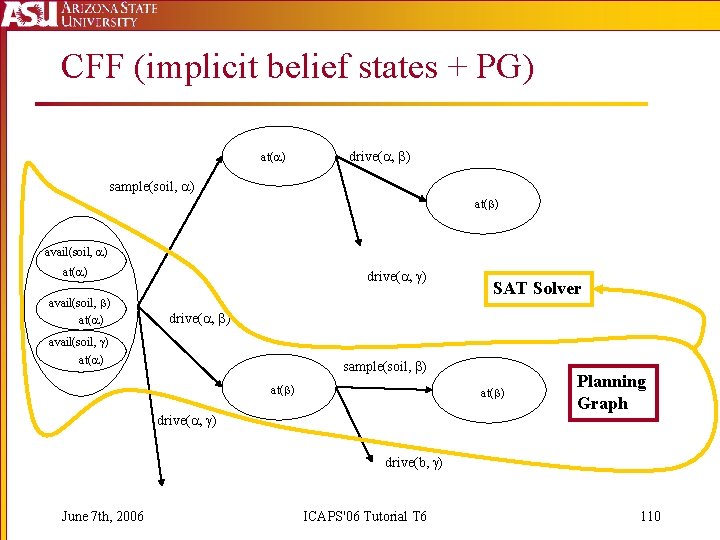
CFF (implicit belief states + PG) at( ) drive( , ) sample(soil, ) at( ) avail(soil, ) at( ) drive( , ) SAT Solver drive( , ) avail(soil, ) at( ) sample(soil, ) at( ) drive( , ) Planning Graph drive(b, ) June 7 th, 2006 ICAPS'06 Tutorial T 6 110

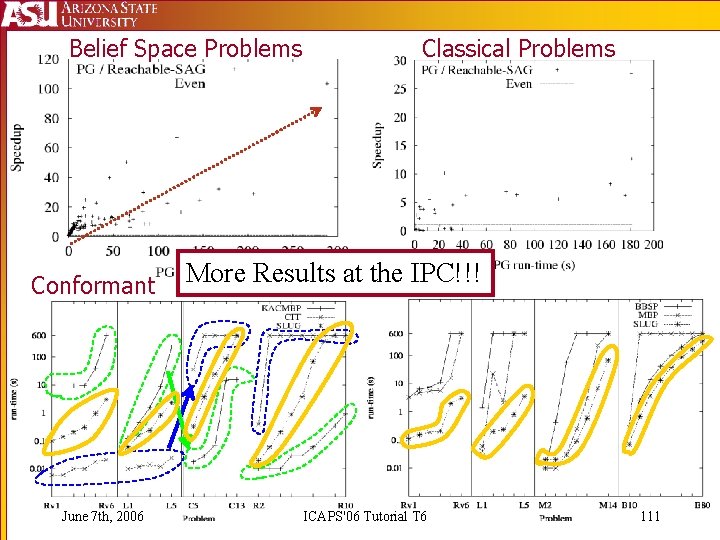
Belief Space Problems Conformant June 7 th, 2006 Classical Problems More Results at the IPC!!! Conditional ICAPS'06 Tutorial T 6 111

Conditional Planning § Actions have Observations § Observations branch the plan because: § Plan Cost is reduced by performing less “just in case” actions – each branch performs relevant actions § Sometimes actions conflict and observing determines which to execute (e. g. , medical treatments) § We are ignoring negative interactions § We are only forced to use observations to remove negative interactions § Ignore the observations and use the conformant relaxed plan § Suitable because the aggregate search effort over all plan branches is related to the conformant relaxed plan cost June 7 th, 2006 ICAPS'06 Tutorial T 6 112

Non-Deterministic Planning Conclusions § Measure positive interaction and independence between states cotransitioning to the goal via overlap § Labeled planning graphs and CFF SAT encoding efficiently measure conformant plan distance § Conformant planning heuristics work for conditional planning without modification June 7 th, 2006 ICAPS'06 Tutorial T 6 113

Stochastic Planning June 7 th, 2006 ICAPS'06 Tutorial T 6 114

Stochastic Rover Example June 7 th, 2006 ICAPS'06 Tutorial T 6 [ICAPS 2006] 115

Search in Probabilistic Belief State Space 0. 04 sample(soil, ) 0. 4 0. 5 0. 1 avail(soil, ) at( ) 0. 36 0. 5 0. 1 avail(soil, ) at( ) have(soil) 0. 36 drive( , ) 0. 5 avail(soil, ) at( ) 0. 1 avail(soil, ) at( ) drive( , ) 0. 4 0. 5 0. 1 June 7 th, 2006 at( ) avail(soil, ) at( ) have(soil) avail(soil, ) at( ) avail(soil, ) sample(soil, ) 0. 04 0. 36 avail(soil, ) at( ) have(soil) 0. 05 avail(soil, ) at( ) 0. 45 avail(soil, ) at( ) have(soil) at( ) drive( , ) 0. 04 avail(soil, ) 0. 1 avail(soil, ) at( ) ICAPS'06 Tutorial T 6 116

Handling Uncertain Actions [ICAPS 2006] § Extending LUG to handle uncertain actions requires label extension that captures: § State uncertainty (as before) § Action outcome uncertainty § Problem: Each action at each level may have a different outcome. The number of uncertain events grows over time – meaning the number of joint outcomes of events grows exponentially with time § Solution: Not all outcomes are important. Sample some of them – keep number of joint outcomes constant. June 7 th, 2006 ICAPS'06 Tutorial T 6 117

Monte Carlo LUG (Mc. LUG) [ICAPS 2006] § Use Sequential Monte Carlo in the Relaxed Planning Space § Build several deterministic planning graphs by sampling states and action outcomes § Represent set of planning graphs using LUG techniques § Labels are sets of particles § Sample which Action outcomes get labeled with particles § Bias relaxed plan by picking actions labeled with most particles to prefer more probable support June 7 th, 2006 ICAPS'06 Tutorial T 6 118

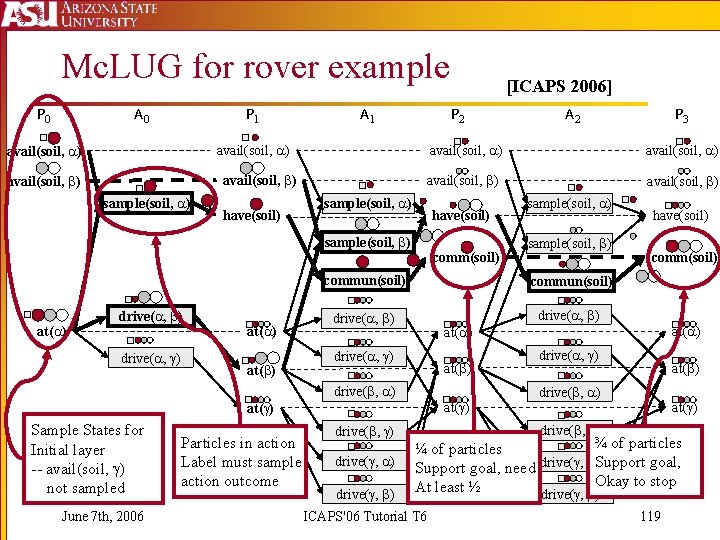
Mc. LUG for rover example P 0 A 0 P 1 A 1 P 2 avail(soil, ) sample(soil, ) have(soil) at( ) drive( , ) at( ) avail(soil, ) sample(soil, ) have(soil) comm(soil) June 7 th, 2006 sample(soil, ) commun(soil) drive( , ) have(soil) comm(soil) at( ) drive( , ) at( ) Particles in action Label must sample action outcome P 3 avail(soil, ) drive( , ) Sample States for Initial layer -- avail(soil, ) not sampled A 2 avail(soil, ) sample(soil, ) drive( , ) [ICAPS 2006] drive( , ) ¾ of particles ¼ of particles Support goal, need drive( , )Support goal, Okay to stop At least ½ drive( , ) ICAPS'06 Tutorial T 6 119

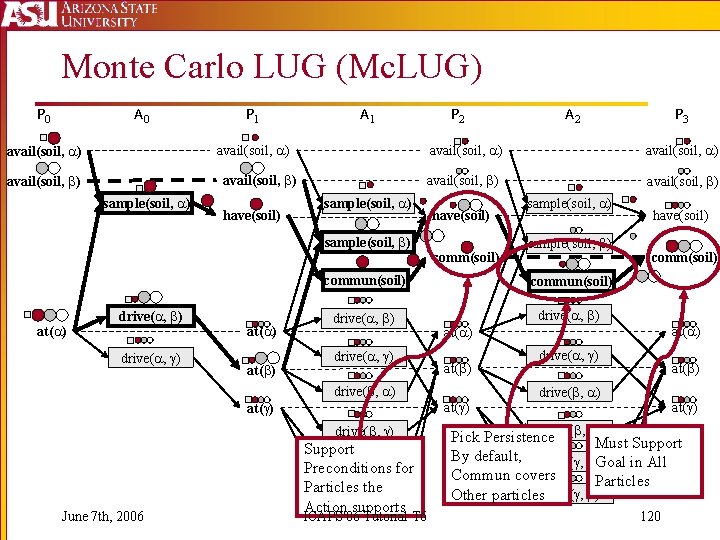
Monte Carlo LUG (Mc. LUG) P 0 A 0 P 1 A 1 P 2 avail(soil, ) sample(soil, ) have(soil) at( ) drive( , ) at( ) avail(soil, ) sample(soil, ) have(soil) comm(soil) sample(soil, ) commun(soil) drive( , ) have(soil) comm(soil) at( ) drive( , ) at( ) at( ) drive( , ) June 7 th, 2006 P 3 avail(soil, ) sample(soil, ) drive( , ) A 2 Support drive( , ) Preconditions for Particles the ) drive( , Action supports ICAPS'06 Tutorial T 6 drive( , ) Pick Persistence Must Support By default, drive( , )Goal in All Commun covers Particles Other particlesdrive( , ) 120

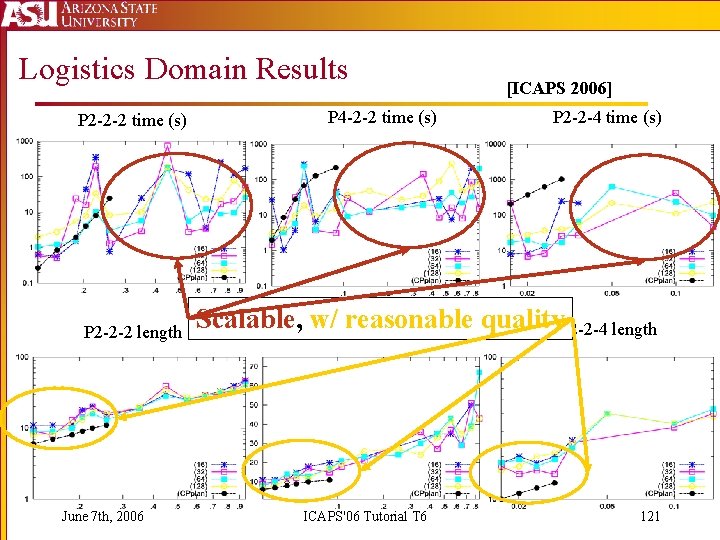
Logistics Domain Results P 2 -2 -2 time (s) P 2 -2 -2 length June 7 th, 2006 P 4 -2 -2 time (s) [ICAPS 2006] P 2 -2 -4 time (s) Scalable, w/P 4 -2 -2 reasonable quality. P 2 -2 -4 length ICAPS'06 Tutorial T 6 121

Grid Domain Results [ICAPS 2006] Grid(0. 8) time(s) Grid(0. 5) time(s) Again, good scalability and quality! Grid(0. 8) length Need More Particles for broad beliefs Grid(0. 5) length June 7 th, 2006 ICAPS'06 Tutorial T 6 122

Direct Probability Propagation § Alternative to label propagation, we can propagate numeric probabilities § Problem: Numeric Propagation tends to assume only independence or positive interaction between actions and propositions. § With probability, we can vastly under-estimate the probability of reaching propositions § Solution: Propagate Correlation – measures pair -wise independence/pos interaction/neg interaction § Can be seen as a continuous mutex June 7 th, 2006 ICAPS'06 Tutorial T 6 123

Correlation § C(x, y) = Pr(x, y)/(Pr(x)Pr(y)) § If : § § § C(x, y) = 0, then x, y are mutex 0< C(x, y) < 1, then x, y interfere C(x, y) = 1, then x, y are independent 1< C(x, y) < 1/Pr(x), then x, y synergize C(x, y) = 1/Pr(x) = 1/Pr(y), then x, y are completely correlated June 7 th, 2006 ICAPS'06 Tutorial T 6 124

Probability of a set of Propositions § Pr(x 1, x 2, …, xn) = i=1. . n Pr(xi|x 1…xi-1) § Pr(xi|x 1…xi-1) = Pr(x 1… xi-1 | xi) Pr(x 1 … xi-1) Pr(x 1|xi) … Pr(xi-1|xi)Pr(xi) Pr(x 1) … Pr(xi-1) = Pr(xi|x 1) … Pr(xi|xi-1) Pr(xi) = Pr(xi) C(xi, x 1)…C(xi, xi-1) = Pr(xi) j = 1. . i-1 C(xi, xj) Chain Rule Bayes Rule Assume Independence Bayes Rule Correlation § Pr(x 1, x 2, …, xn) = i=1. . n Pr(xi) j = 1. . i-1 C(xi, xj) June 7 th, 2006 ICAPS'06 Tutorial T 6 125

Probability Propagation § The probability of an Action being enabled is the probability of its preconditions (a set of propositions). § The probability of an effect is the product of the action probability and outcome probability § A single (or pair of) proposition(s) has probability equal to the probability it is given by the best set of supporters. § The probability that a set of supporters gives a proposition is the sum over the probability of all possible executions of the actions. June 7 th, 2006 ICAPS'06 Tutorial T 6 126

Results June 7 th, 2006 ICAPS'06 Tutorial T 6 127

Stochastic Planning Conclusions § Number of joint action outcomes too large § Sampling outcomes to represent in labels is much faster than exact representation § SMC gives us a good way to use multiple planning graph for heuristics, and the Mc. LUG helps keep the representation small § Numeric Propagation of probability can better capture interactions with correlation § Can extend to cost and resource propagation June 7 th, 2006 ICAPS'06 Tutorial T 6 128

Hybrid Planning Models June 7 th, 2006 ICAPS'06 Tutorial T 6 129

Hybrid Models § Metric-Temporal w/ Resources (SAPA) § Temporal Planning Graph w/ Uncertainty (Prottle) § PSP w/ Resources (SAPAMPS) § Cost-based Conditional Planning (CLUG) June 7 th, 2006 ICAPS'06 Tutorial T 6 130

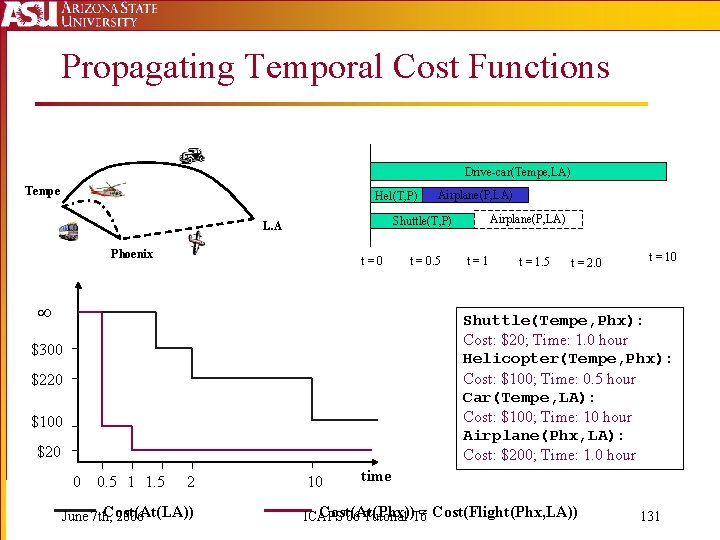
Propagating Temporal Cost Functions Drive-car(Tempe, LA) Tempe Hel(T, P) Airplane(P, LA) Shuttle(T, P) L. A Phoenix t=0 t = 0. 5 t=1 t = 1. 5 t = 2. 0 t = 10 Shuttle(Tempe, Phx): Cost: $20; Time: 1. 0 hour Helicopter(Tempe, Phx): Cost: $100; Time: 0. 5 hour Car(Tempe, LA): Cost: $100; Time: 10 hour Airplane(Phx, LA): Cost: $200; Time: 1. 0 hour $300 $220 $100 $20 0 0. 5 1 1. 5 2 Cost(At(LA)) June 7 th, 2006 10 time Cost(At(Phx)) = Cost(Flight(Phx, LA)) ICAPS'06 Tutorial T 6 131

Heuristics based on cost functions Using Relaxed Plan Direct § If we want to minimize makespan: § h = t 0 § If we want to minimize cost § h = Cost. Aggregate(G, t ) § If we want to minimize a function f(time, cost) of cost and makespan § h = min f(t, Cost(G, t)) s. t. t 0 t t § E. g. f(time, cost) = 100. makespan + Cost then h = 100 x 2 + 220 at t 0 t = 2 t § Extract a relaxed plan using h as the bias § If the objective function is f(time, cost), then action A ( to be added to RP) is selected such that: f(t(RP+A), C(RP+A)) + f(t(Gnew), C(Gnew)) is minimal Gnew = (G Precond(A)) Effects) cost $300 $220 Cost(At(LA)) $100 Time of lowest cost 0 June 7 th, 2006 Time of Earliest achievement t 0=1. 5 ICAPS'06 Tutorial T 6 2 t = 10 time 132

Phased Relaxation The relaxed plan can be adjusted to take into account constraints that were originally ignored Adjusting for Mutexes: Adjust the make-span estimate of the relaxed plan by marking actions that are mutex (and thus cannot be executed concurrently Adjusting for Resource Interactions: Estimate the number of additional resource-producing actions needed to make-up for any resource short-fall in the relaxed plan C = C + R (Con(R) – (Init(R)+Pro(R)))/ R * C(AR) June 7 th, 2006 ICAPS'06 Tutorial T 6 133

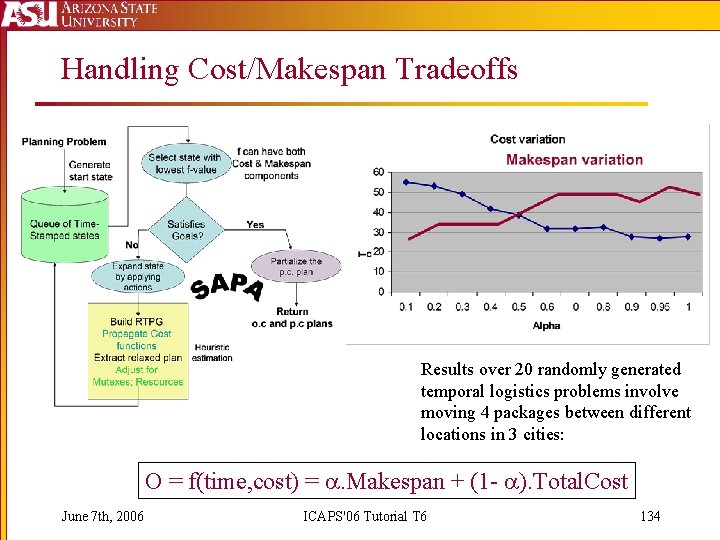
Handling Cost/Makespan Tradeoffs Results over 20 randomly generated temporal logistics problems involve moving 4 packages between different locations in 3 cities: O = f(time, cost) = . Makespan + (1 - ). Total. Cost June 7 th, 2006 ICAPS'06 Tutorial T 6 134

Prottle § SAPA-style (time-stamped states and event queues) search for fully-observable conditional plans using L-RTDP § Optimize probability of goal satisfaction within a given, finite makespan § Heuristic estimates probability of goal satisfaction in the plan suffix June 7 th, 2006 ICAPS'06 Tutorial T 6 135

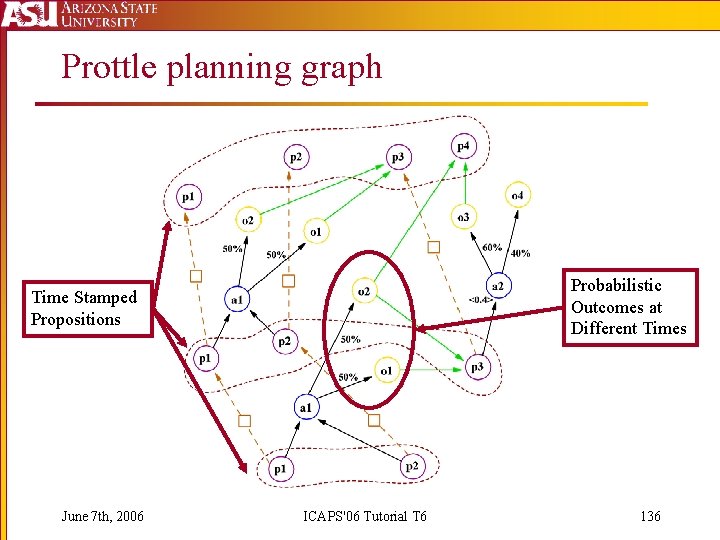
Prottle planning graph Probabilistic Outcomes at Different Times Time Stamped Propositions June 7 th, 2006 ICAPS'06 Tutorial T 6 136

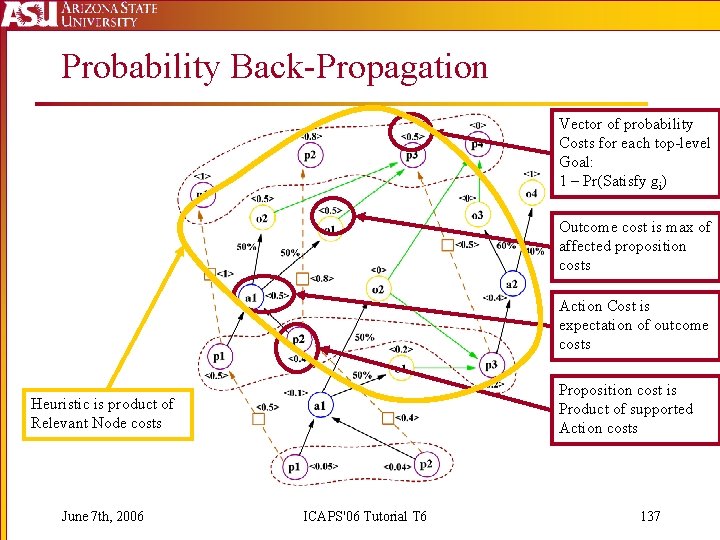
Probability Back-Propagation Vector of probability Costs for each top-level Goal: 1 – Pr(Satisfy gi) Outcome cost is max of affected proposition costs Action Cost is expectation of outcome costs Proposition cost is Product of supported Action costs Heuristic is product of Relevant Node costs June 7 th, 2006 ICAPS'06 Tutorial T 6 137

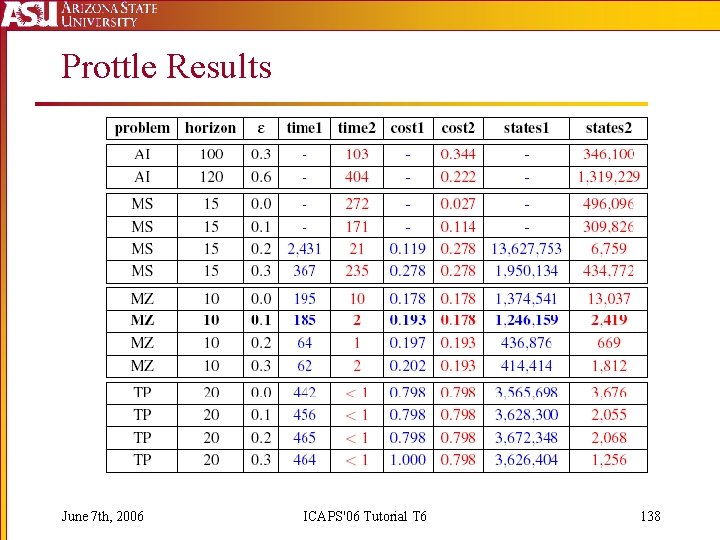
Prottle Results June 7 th, 2006 ICAPS'06 Tutorial T 6 138

PSP w/ Resources § Utility and Cost based on the values of resources § Challenges: § Need to propagate cost for resource intervals § Need to support resource goals at different levels June 7 th, 2006 ICAPS'06 Tutorial T 6 139

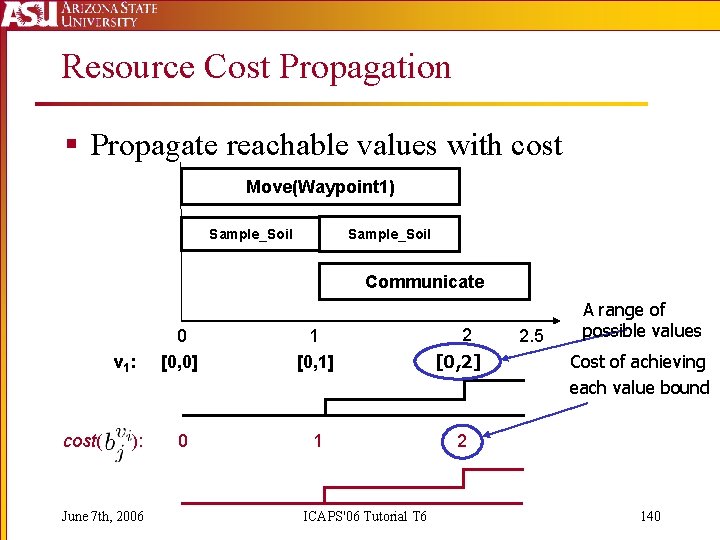
Resource Cost Propagation § Propagate reachable values with cost Move(Waypoint 1) Sample_Soil Communicate v 1 : cost( ): June 7 th, 2006 0 [0, 0] 1 [0, 1] 2 [0, 2] 0 1 2 ICAPS'06 Tutorial T 6 2. 5 A range of possible values Cost of achieving each value bound 140

Cost Propagation on Variable Bounds Sample_Soil Effect: v 1+=1 § Bound cost dependent upon § action cost § previous bound cost - current bound cost adds to the next § Cost of all bounds in expressions Sample_Soil v 1: [0, 0] Sample_Soil [0, 1] [0, 2] Cost(v 1=2) C(Sample_Soil)+Cost(v 1=1) Sample_Soil Effect: v 1+=v 2 Sample_Soil v 1: [0, 0] v 2: [0, 3] Sample_Soil [0, 3] [0, 6] Cost(v 1=6) C(Sample_Soil)+Cost(v 2=3)+Cost(v 1=3) June 7 th, 2006 ICAPS'06 Tutorial T 6 141

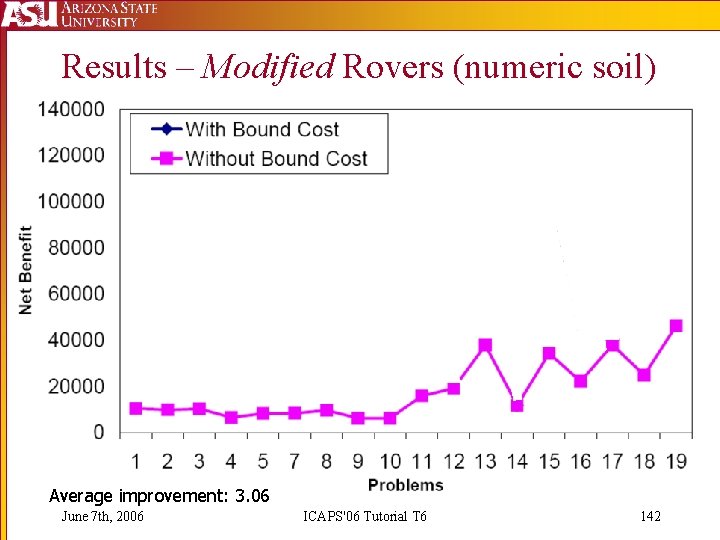
Results – Modified Rovers (numeric soil) Average improvement: 3. 06 June 7 th, 2006 ICAPS'06 Tutorial T 6 142

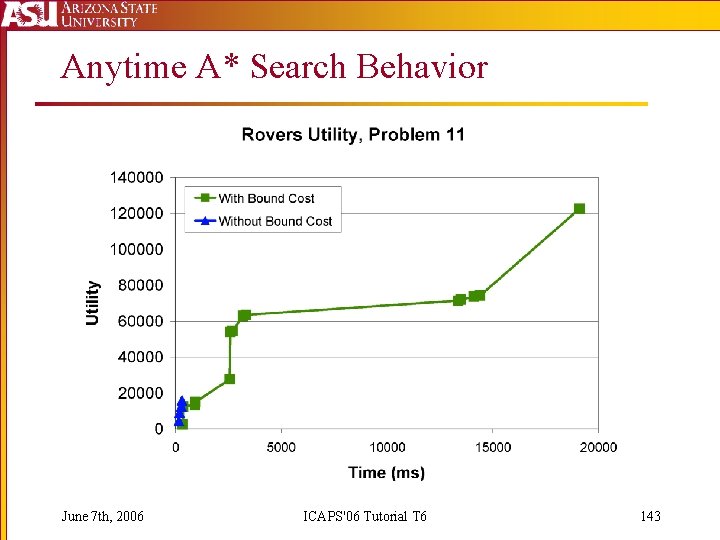
Anytime A* Search Behavior June 7 th, 2006 ICAPS'06 Tutorial T 6 143

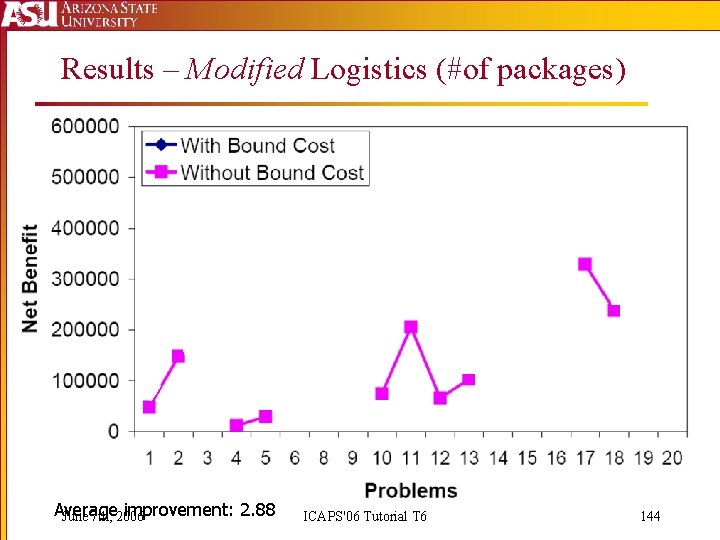
Results – Modified Logistics (#of packages) Average improvement: 2. 88 June 7 th, 2006 ICAPS'06 Tutorial T 6 144

Cost-Based Conditional Planning § Actions may reduce uncertainty, but cost a lot § Do we want more “just in case” actions that are cheap, or less that are more expensive § Propagate Costs on the LUG (CLUG) § Problem: LUG represents multiple explicit planning graphs and the costs can be different in each planning graph. § A single cost for every explicit planning assumes full positive interaction § Multiple costs, one for each planning graph is too costly § Solution: Propagate cost for partitions of the explicit planning graphs June 7 th, 2006 ICAPS'06 Tutorial T 6 145

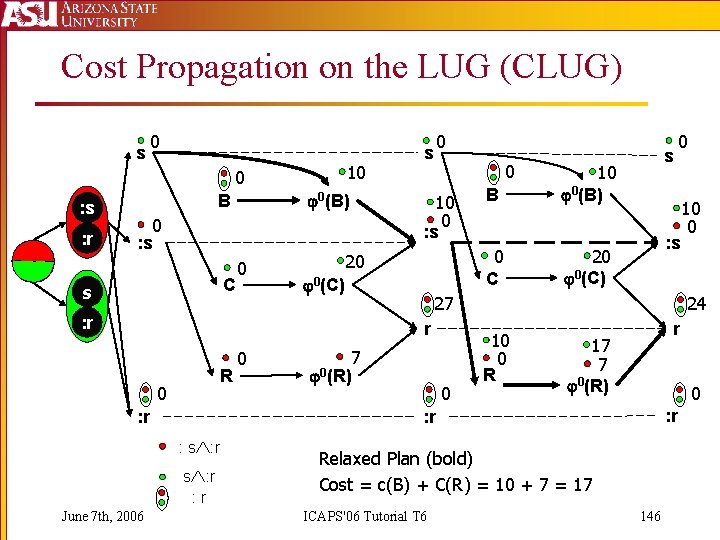
Cost Propagation on the LUG (CLUG) s 0 0 : s : r 0(B) B 0 : s C s 10 0 s 0 10 0 : s 20 0(C) : r 0 R 0 : r 20 0(C) : s 7 0(R) 0 s : r 10 0 R r 17 7 0(R) 0 : r Relaxed Plan (bold) Cost = c(B) + C(R) = 10 + 7 = 17 ICAPS'06 Tutorial T 6 10 0 24 : r : s : r June 7 th, 2006 0 C 27 r 0 B 10 0(B) s 0 146

The Medical Specialist [Bryce & Kambhampati, 2005] High Cost Sensors Low Cost Sensors Using Propagated Costs Improves Plan Quality, Average Path Cost Total Time Without much additional time June 7 th, 2006 ICAPS'06 Tutorial T 6 147

Overall Conclusions § Relaxed Reachability Analysis § Concentrate strongly on positive interactions and independence by ignoring negative interaction § Estimates improve with more negative interactions § Heuristics can estimate and aggregate costs of goals or find relaxed plans § Propagate numeric information to adjust estimates § Cost, Resources, Probability, Time § Solving hybrid problems is hard § Extra Approximations § Phased Relaxation § Adjustments/Penalties June 7 th, 2006 ICAPS'06 Tutorial T 6 148

Why do we love PG Heuristics? § They work! § They are “forgiving” § § You don't like doing mutex? okay You don't like growing the graph all the way? okay. § Allow propagation of many types of information § Level, subgoal interaction, time, cost, world support, probability § Support phased relaxation § E. g. Ignore mutexes and resources and bring them back later… § Graph structure supports other synergistic uses § e. g. action selection § Versatility… June 7 th, 2006 ICAPS'06 Tutorial T 6 149

Versatility of PG Heuristics § PG Variations § § Serial Parallel Temporal Labelled § Planning Problems § Classical § Resource/Temporal § Conformant June 7 th, 2006 § Propagation Methods § § Level Mutex Cost Label § Planners § § ICAPS'06 Tutorial T 6 Regression Progression Partial Order Graphplan-style 150