PLANILANDIA un maravilloso mundo en dos dimensiones ngel

PLANILANDIA, un maravilloso mundo en dos dimensiones Ángel Ferrández Izquierdo Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología

Hagamos un ejercicio de imaginación: Cada uno de nosotros se va convertir por un momento en un muñeco de plastilina que se dejará aplastar por una apisonadora vertical de cabeza a pies. ¿Qué verán quienes entren al salón? Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 2

Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 3

Arreglemos un poco las figuras que aparecieron sobre la mesa Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 4

Hagamos un juego: Con una varita mágica le daremos vida a todos esos polígonos – que son nuestras representaciones bidimensionales - e imaginemos cómo vivirían haciendo su vida con sólo dos posibilidades de movimiento: A n Febrero de 2006 IES Floridablanca lo lo largo ancho 2ª Semana de la Ciencia y la Tecnología 5

Este es el comienzo de una historia apasionante. Érase una vez una muy, lejana tierra, llamada PLANILANDIA, cuyos habitantes eran - Segmentos (de línea recta) y figuras planas - Triangulares, Cuadradas, Pentagonales - Hexagonales, … - Polígonos de 50 lados, … - Polígonos de 700 lados, … - Polígonos de 1444 lados, … - Círculos Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 6

El autor: Edwin Abbot (1838 -1926), alias A. Square Fue un eclesiástico inglés, estudioso de Shakespeare, cuya verdadera vocación eran las Matemáticas, maestro y director de escuela e intelectual muy apreciado. Experto en literatura clásica y teología. Seudónimo: ? ? ? La obra: sátira de la Inglaterra de su época Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 7

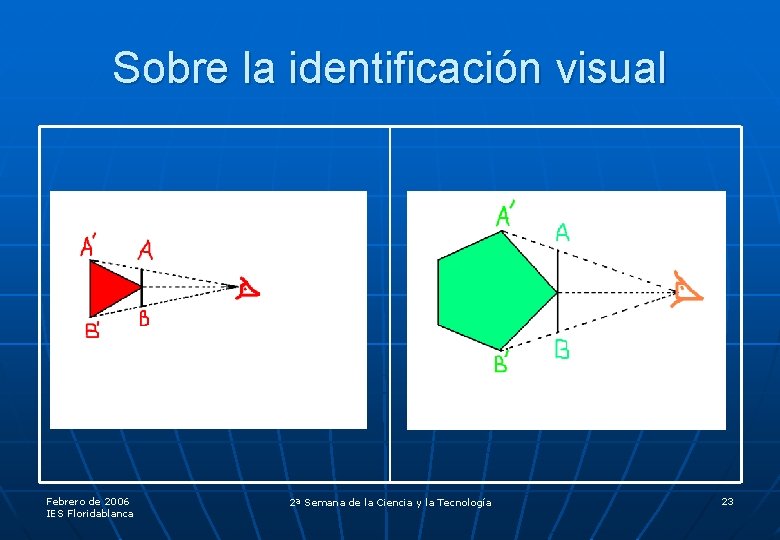
Se trata de un relato en primera persona. Es decir, uno de los personajes – un cuadrado - es quien cuenta la historia. ¿Cómo hemos de imaginar a los personajes? Coloquemos una moneda en una mesa y la miramos desde una posición perpendicular a la mesa (la veremos redonda). Movemos el ojo hasta la rasante de la mesa (y veremos un trozo de recta o segmento) Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 8

La clase social más baja: los segmentos de recta o mujeres Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 9

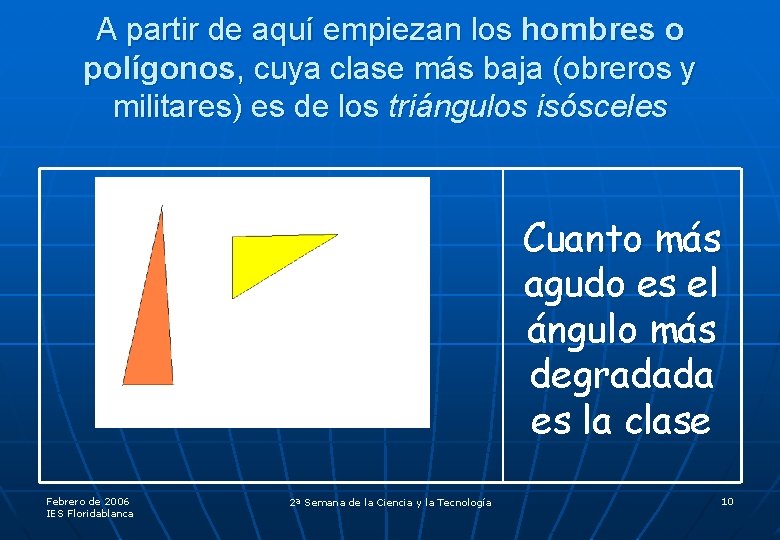
A partir de aquí empiezan los hombres o polígonos, cuya clase más baja (obreros y militares) es de los triángulos isósceles Cuanto más agudo es el ángulo más degradada es la clase Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 10

La clase media (los comerciantes): los triángulos equiláteros Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 11

Por encima: los cuadrados, pentágonos, hexágonos, etc. , que se trata de los profesionales (abogados, médicos, profesores, etc. ) y caballeros Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 12

La nobleza: condes, duques, etc. a partir de seis lados Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 13

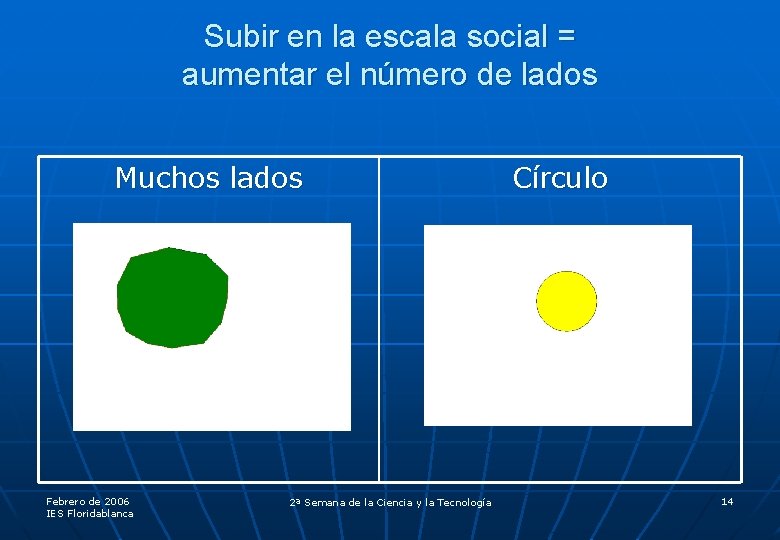
Subir en la escala social = aumentar el número de lados Muchos lados Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología Círculo 14

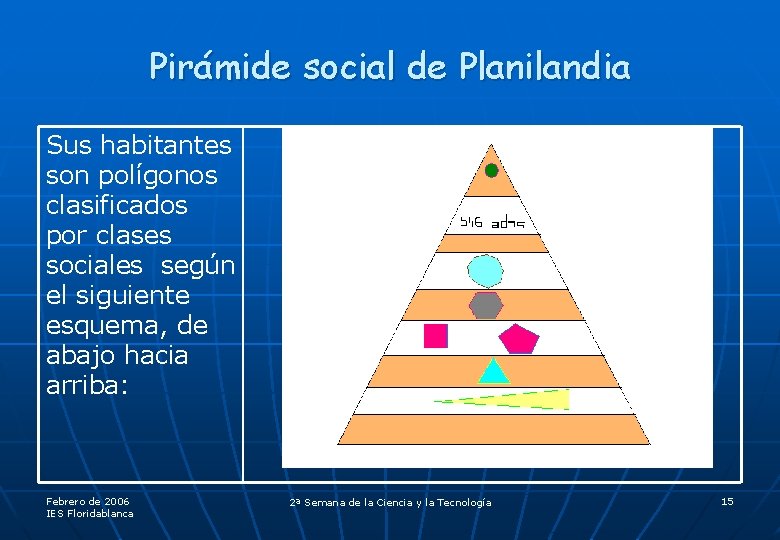
Pirámide social de Planilandia Sus habitantes son polígonos clasificados por clases sociales según el siguiente esquema, de abajo hacia arriba: Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 15

Regla general: El aumento en el número de lados significa: n Aumento en la posición social n Aumento de poder n Disminución de la fertilidad Y PRINCIPALMENTE Aumento de inteligencia Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 16

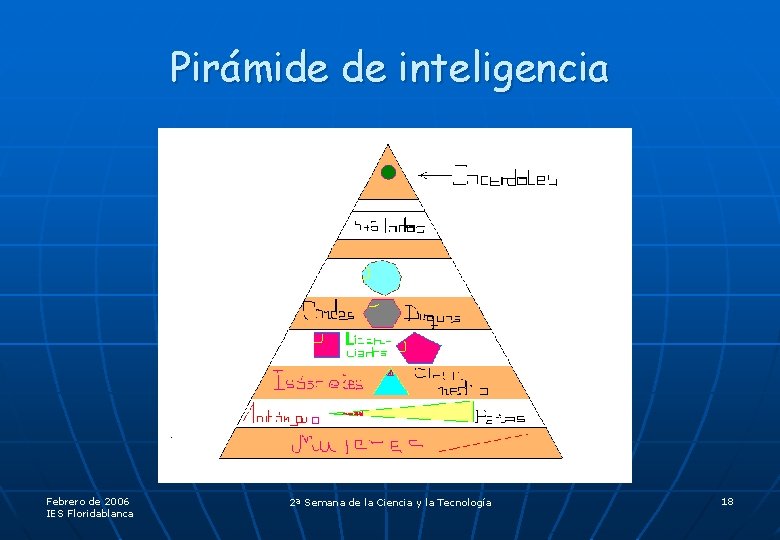
¿Cómo “miden” la inteligencia los planilandeses? MIDIENDO SU ÁNGULO MÁS AGUDO, QUE ELLOS LLAMAN CEREBRO : A mayor “cerebro” corresponde mayor inteligencia Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 17

Pirámide de inteligencia Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 18

Principio básico del Estado: “TODO SER HUMANO DE PLANILANDIA ES UNA FIGURA REGULAR” ¡ Así pues, los “seres humanos” comienzan con la clase de los equiláteros ! Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 19

La descendencia Regla básica: un hijo varón siempre tiene un lado más que su padre El hijo de un equilátero siempre será equilátero El hijo de un isósceles siempre será isósceles Excepción habitual: Excepción muy rara: El hijo de un equilátero El hijo de un isósceles es un cuadrado es un equilátero Febrero de 2006 2ª Semana de la Ciencia y la Tecnología IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 20

¿Cómo evolucionan? El tamaño de los lados se corresponde con la edad del individuo Mujeres Hombres Bebé: ≈ 2, 5 cm Suma de sus lados: ≈ 60 cm Adulta: ≈ 30 cm Cerebro de las clases más bajas va desde 0, 5º hasta 60º Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 21

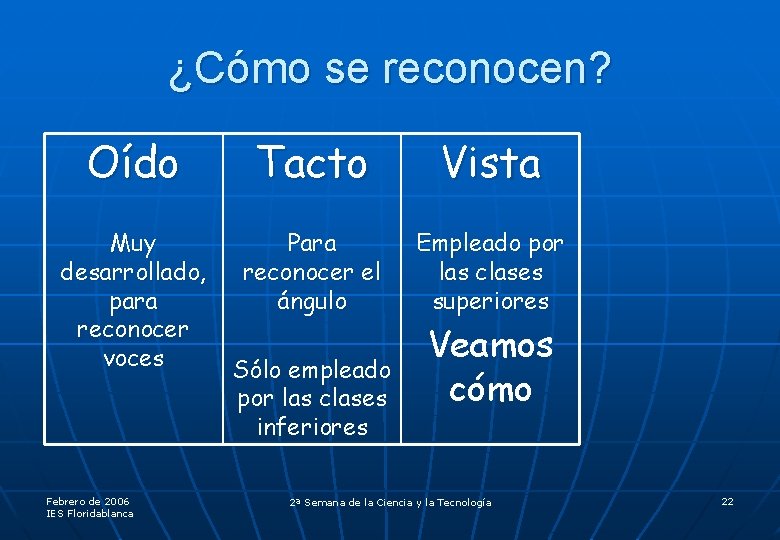
¿Cómo se reconocen? Oído Tacto Vista Muy desarrollado, para reconocer voces Para reconocer el ángulo Empleado por las clases superiores Febrero de 2006 IES Floridablanca Sólo empleado por las clases inferiores Veamos cómo 2ª Semana de la Ciencia y la Tecnología 22

Sobre la identificación visual Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 23

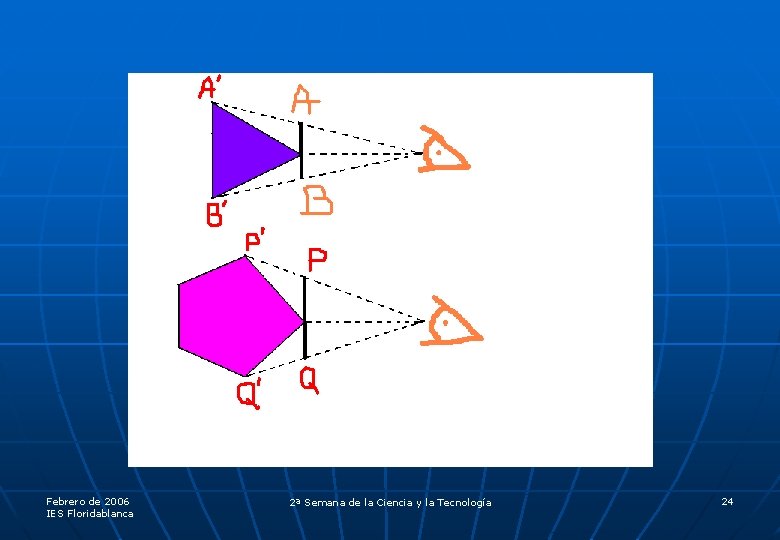
Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 24

Sobre las figuras irregulares: ¡ absolutamente prohibidas ! No se podría conocer su diagonal y así no ese podrías saber si pueden entrar en las casas Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 25

¿Cómo son las casas? Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 26

Los sacerdotes n n Clase gobernante Administradores de la educación, las artes y las ciencias; el comercio y las industrias; la obra pública; el ejército; la moralidad y la teología. Son la causa impulsora de todo: los que piensan, para que los otros hagan. El círculo jefe tiene, actualmente, 10. 000 lados Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 27

Segunda parte n Linealandia: un mundo unidimensional ¿ lo podéis imaginar ? n Espaciolandia: un mundo tridimensional Nuestro mundo Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 28

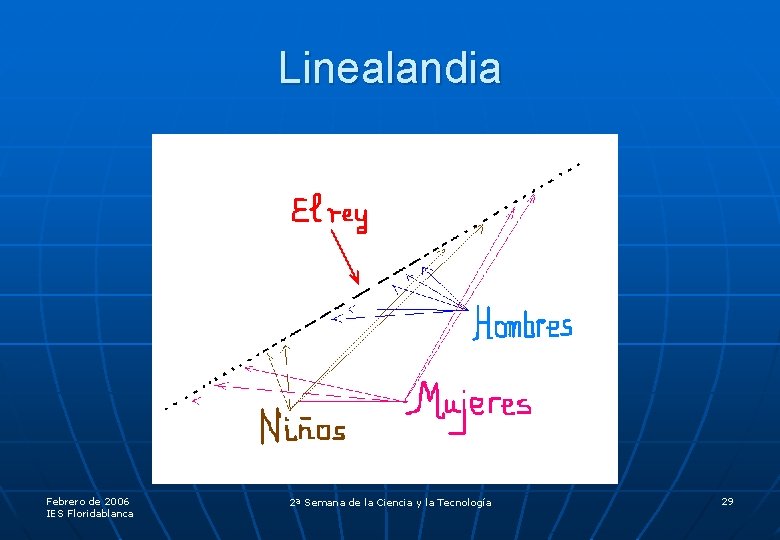
Linealandia Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 29

El sueño de A. Square (I) Visita a Linealandia y trata de explicar al rey cómo es la vida en Planilandia. ¿Cómo reconocerían los habitantes de Linealandia a los de Planilandia? Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 30

El sueño de A. Square (II) Una visita a Espaciolandia, donde encuentra algo sorprendente: Los seres humanos, además de ser largos y anchos, ¡ son altos ! ¿Cómo reconocerían los habitantes de Planilandia a los de Espaciolandia? Febrero de 2006 IES Floridablanca 2ª Semana de la Ciencia y la Tecnología 31