Planet Earth Modeling in Matlab Richiami dal laboratorio

Planet Earth Modeling in Matlab Richiami dal laboratorio di Informatica a. a. 2020 -2021 Alcuni esempi che illustrano come vengono applicate le tecniche avete visto finora nella parte 1 del corso, tenuta dal prof. Eugenio Omodeo. Docente: Prof. Carla Braitenberg, Ricerca dei minimi in collaborazione con Dott. Alberto Pastorutti Dipartimento Matematica e Geoscienze, Via Weiss 1, Università di Trieste E-mail: berg@units. it Tel. 040 5582258

Tecniche discusse finora durante le ore del prof. Omodeo 1) Trovare il minimo di una funzione o di una serie temporale: – fminsearch (ricerca libera) – fminbnd (ricerca entro limiti prefissati) 2) Interpolare dati con una funzione di Matlab: Interp 1 3) Trovare i coefficienti di una funzione nota per fittare dati osservati: fmincon La funzione e’ del tipo: y 1 = c 1(1) * x. ^3 + c 1(2) * x. ^2 + c 1(3) * x + c 1(4);

Possibili applicazioni • 1) Minimo/Massimo di una serie temporale di dati osservati. • I dati potrebbero essere la temperatura ambientale, il livello del mare, il movimento del clinometro in Grotta Gigante, la misura dell’inclinazione di un versante monitorato perche’ franoso • Noi mostriamo l’esempio del livello di acqua nel pozzo di Trebiciano. Ci sono delle piene, e sarebbe utile trovare i tempi delle piene, per farne poi una statistica. Come livello massimo e frequenza nell’arco di un anno. Importante per il pericolo dell’inquinamento della falda acquifera.

Minimo-massimo in 2 D • Altra situazione e’ quella di avere delle osservazioni sul piano, per osservazioni in funzione di longitudine e latitudine. Per esempio la topografia. Potrebbe anche essere la temperatura sul territorio. Dobbiamo trovare i valori estremi, quelli massimi o quelli minimi. Come esempio mostreremo la ricerca delle doline in zona del Carso partendo dalla topografia.

2) Interpolazione di valori noti • Puo’ succedere che i dati osservati non siano disponibili ad intervalli regolari, ma siano stati presi a tempi irregolari. Per molte successive analisi invece e’ necessario avere una serie di osservazioni ad intervalli regolari, per esempio osservazioni al secondo, al minuto, oppure all’ora. In quel caso i dati osservati devono essere interpolati. E’ una applicazione che serve molto di frequente.

3) Fittare una funzione nota a delle osservazioni • Avete imparato a fittare una funzione nota ad una serie di punti osservati. Il problema consiste nel trovare i coefficienti della funzione, cosi’ che meglio rappresenta le osservazioni. Questo e’ un problema molto importante, e troviamo moltissimi esempi che lo rappresentano. • Per esempio abbiamo la serie temporale del mareografo di Trieste, e dobbiamo definire il tasso di incremento lineare medio, le variazioni a lungo periodo, e abbiamo bisogno di separare le variazioni lente dalle variazioni veloci, ma con ampiezze molto piu’ piccole. y 1 = c 1(1) * x. ^3 + c 1(2) * x. ^2 + c 1(3) * x + c 1(4); Il coefficiente lineare ci da’ il tasso lineare medio: l’incremento medio del livello del mare in unità tempo. Se ii dati hanno l’asse temporale in anni decimali, e la misura in millimetri, il tasso sara’ in millimetri all’anno. Possiamo sottrarre la funzione y 1(t) dalle osservazioni, per mettere in evidenza le variazioni veloci.

Fittare le oscillazioni a frequenze note di una variazione di parametro ambientale Una situazione tipica: l’osservazione presenta oscillazioni a frequenze note (periodo solare, periodo di maree, ciclo settimanale (influenza antropogenica) y 1 = c(1) * cos (c(2) *2*pi/T 1*t+ c(3) ) + c(4) * cos (c(5) *2*pi/T 1*t+ c(6) ) I coefficienti possono essere trovati con fmincon, fittando le osservazioni.

Due esempi nei quali si utilizzano le tecniche sono state introdotte nella prima parte del corso • 1 Cercare gli estremi della serie temporale nel pozzo di Trebiciano, zona Carsica • 2 Cercare le Doline nel terreno Carsico Triestino.

Esercizio livello acqua nell’Abisso di Trebiciano • Anni di osservazione: 2006 -2008, un campione ogni ora. Unita’ di misura: m sopra il livello del mare. • Caricare il file. Nome dell’array: liv_Trebiciano load('livello_Abisso. Trebiciano_Tdec_CORRETTO. mat'); • Determinare valore medio, valore massimo e data del valore massimo • Comandi necessari: • max(livello_tdec): cerca il massimo sulla quinta colonna, comprendente il livello. • mean(livello_tdec) • std(livello_tdec)

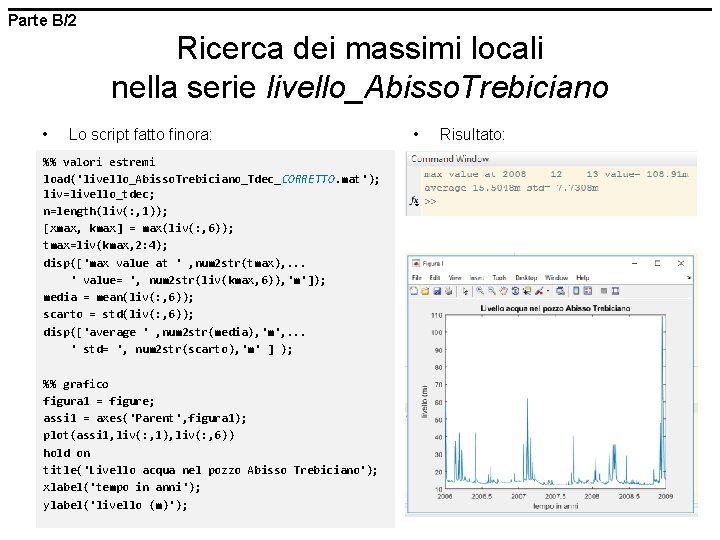
Parte B/2 Ricerca dei massimi locali nella serie livello_Abisso. Trebiciano • Lo script fatto finora: %% valori estremi load('livello_Abisso. Trebiciano_Tdec_ CORRETTO. mat'); liv=livello_tdec; n=length(liv(: , 1)); [xmax, kmax] = max(liv(: , 6)); tmax=liv(kmax, 2: 4); disp(['max value at ' , num 2 str(tmax), . . . ' value= ', num 2 str(liv(kmax, 6)), 'm']); media = mean(liv(: , 6)); scarto = std(liv(: , 6)); disp(['average ' , num 2 str(media), 'm', . . . ' std= ', num 2 str(scarto), 'm' ] ); %% grafico figura 1 = figure; assi 1 = axes('Parent', figura 1); plot(assi 1, liv(: , 1), liv(: , 6)) hold on title('Livello acqua nel pozzo Abisso Trebiciano'); xlabel('tempo in anni'); ylabel('livello (m)'); • Risultato:

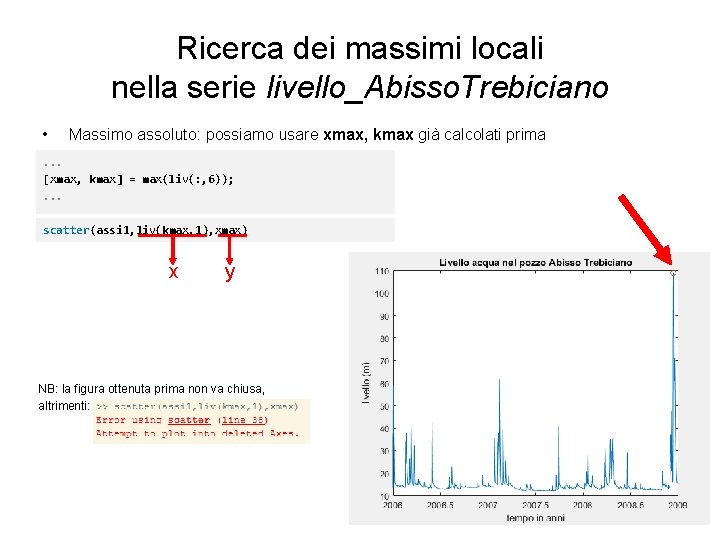
Ricerca dei massimi locali nella serie livello_Abisso. Trebiciano • Massimo assoluto: possiamo usare xmax, kmax già calcolati prima . . . [xmax, kmax] = max(liv(: , 6)); . . . scatter(assi 1, liv(kmax, 1), xmax) x y NB: la figura ottenuta prima non va chiusa, altrimenti:

Ricerca dei massimi locali nella serie livello_Abisso. Trebiciano • 1 2 3 4 5 6 7 cercare i primi n valori più grandi: definiamo una funzione function [M, I] = maxsort(in, n) M = zeros(1, n); I = M; for i=1: n [M(i), I(i)] = max(in); in(I(i)) = 0; end • Salvate la function in un file con lo stesso nome della chiamata, quindi maxsort. m «Ottieni il valore M e l’indice I degli n valori più grandi di in. » Nella riga 2 vengono creati M ed I, vettori lunghi n, composti di soli zeri. Le righe da 3 a 6 appartengono a un ciclo for: ad ogni iterazione viene calcolato l’n-esimo massimo e il suo indice, quindi quell’elemento di in viene sostituito con zero.

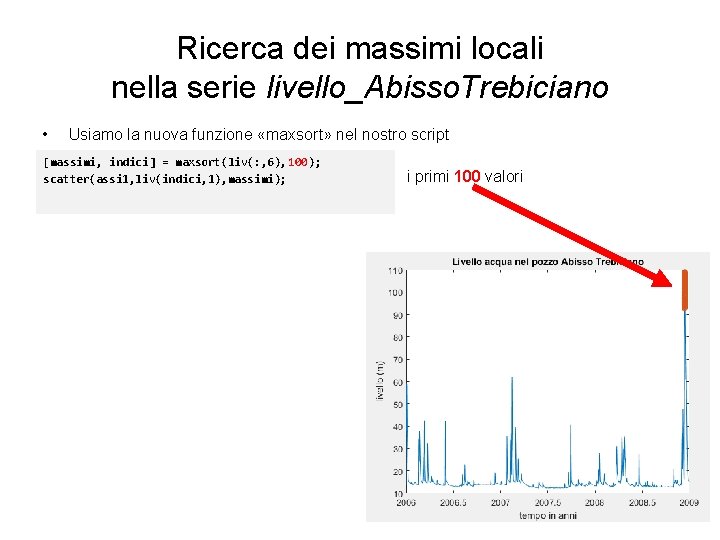
Ricerca dei massimi locali nella serie livello_Abisso. Trebiciano • Usiamo la nuova funzione «maxsort» nel nostro script [massimi, indici] = maxsort(liv(: , 6), 100); scatter(assi 1, liv(indici, 1), massimi); i primi 100 valori

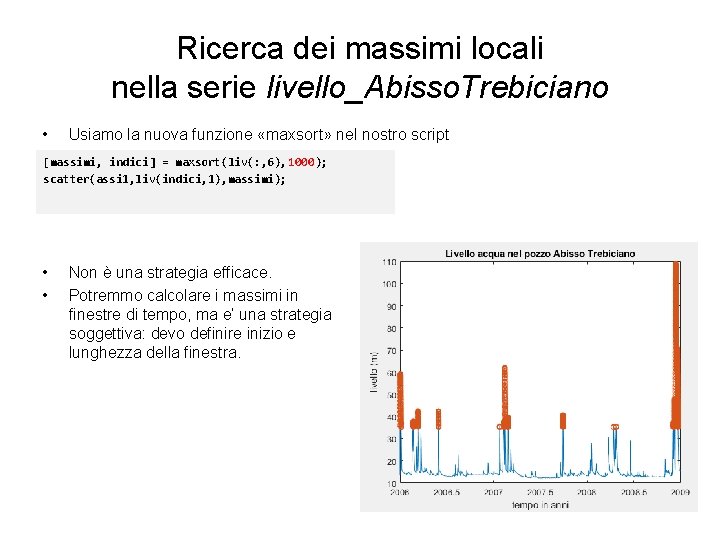
Ricerca dei massimi locali nella serie livello_Abisso. Trebiciano • Usiamo la nuova funzione «maxsort» nel nostro script [massimi, indici] = maxsort(liv(: , 6), 1000); scatter(assi 1, liv(indici, 1), massimi); • • Non è una strategia efficace. Potremmo calcolare i massimi in finestre di tempo, ma e’ una strategia soggettiva: devo definire inizio e lunghezza della finestra.

Ricerca dei massimi locali nella serie livello_Abisso. Trebiciano • • • Un altro metodo: calcoliamo le derivate prima e seconda Cerchiamo i punti in cui – la derivata prima è zero (entro una tolleranza) – la derivata seconda è negativa (concavità verso l’alto) Produciamo tre grafici sovrapposti, usando subplot Calcoliamo la derivata (numerica) con diff: step_livelli = liv(2: end, 1) - liv(1: end-1, 1); der 1 = diff(liv(: , 6)). / step_livelli; der 2 = diff(der 1). / step_livelli(1: end-1); der 1 = der 1(1: end-1); in questa maniera usiamo il passo corretto tra due campioni, che non è costante dopo aver calcolato diff, il risultato è più corto di un elemento. Rendiamo la derivata 1° lunga quanto la derivata 2°, togliendo l’ultimo elemento (fermandoci a end-1) Dal help di matlab: diff(X), for a vector X, is [X(2)-X(1) X(3)-X(2). . . X(n)-X(n-1)].

Ricerca dei massimi locali nella serie livello_Abisso. Trebiciano • • • Approssimiamo la derivata prima «uguale a zero» entro una tolleranza (più o meno tol_der 1) Approssimiamo la derivata seconda «negativa» entro una tolleranza (minore di tol_der 2) Teniamo solo i massimi locali trovati che sono superiori a tol_liv tol_der 1 = 1. 25 e 3; tol_der 2 = -0. 001; tol_liv = 20; massimi_locali = find(and(and(der 1<=tol_der 1, der 1>=-tol_der 1), . . . der 2<=tol_der 2), . . . liv(1: end-2, 6)>=tol_liv));

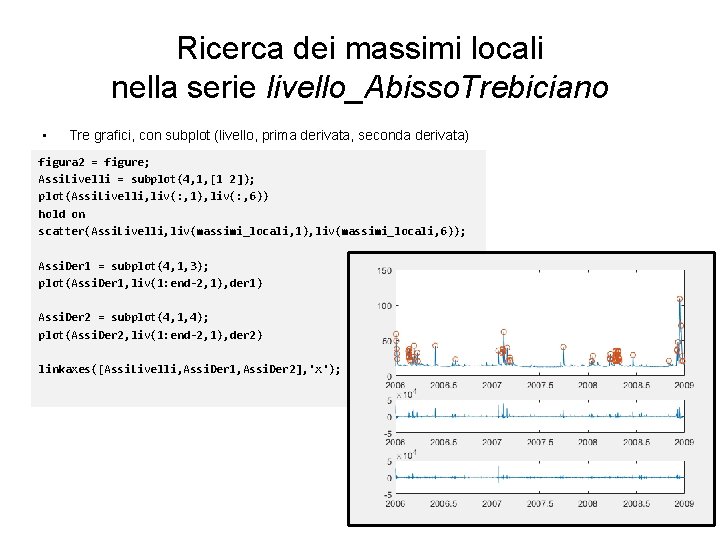
Ricerca dei massimi locali nella serie livello_Abisso. Trebiciano • Tre grafici, con subplot (livello, prima derivata, seconda derivata) figura 2 = figure; Assi. Livelli = subplot(4, 1, [1 2]); plot(Assi. Livelli, liv(: , 1), liv(: , 6)) hold on scatter(Assi. Livelli, liv(massimi_locali, 1), liv(massimi_locali, 6)); Assi. Der 1 = subplot(4, 1, 3); plot(Assi. Der 1, liv(1: end-2, 1), der 1) Assi. Der 2 = subplot(4, 1, 4); plot(Assi. Der 2, liv(1: end-2, 1), der 2) linkaxes([Assi. Livelli, Assi. Der 1, Assi. Der 2], 'x');

Richiamo sull’utilizzo di un Modello digitale del terreno • Nella esercitazione del corso di informatica per Geologia abbiamo utilizzato due database. Trovate gli script ed i database su moodle: • DTM in coordinate geografiche alta risoluzione e bassa risoluzione • DTM_ortom_regrid 10 m_WGS 84_HD. mat • DTM_ortom_regrid 10 m_WGS 84_LD. mat • DTM alta risoluzione in coordinate cartesiane • DTM_esercizio 3. mat

Modello digitale del terreno FVG

Rappresentazione grafica del modello digitale del terreno • Scopo dell’esercizio: • Utilizzare il modello digitale del terreno in zona carsica • - rappresentare il modello digitale del terreno in 3 D • - calcolare le isolinee di quota

Grafico della topografia in 3 D %Plot_Topografia 3 D %caricamento dati digitali del terreno load DTM_ortom_regrid 10 m_WGS 84_HD. mat; figure %surface plot surf(X 1, Y 1, Z 1) shading interp; % visualizzazione 3 D (azimuth -78°, elevation 62°) view([-78, 62]); % etichette sugli assi xlabel('asse orizzantale X'); ylabel('asse verticale Y'); zlabel('asse Z quota');

Comando View • view(az, el) and view([az, el]) set the viewing angle for a three-dimensional plot. The azimuth, az, is the horizontal rotation about the z-axis as measured in degrees from the negative y-axis. Positive values indicate counterclockwise rotation of the viewpoint. el is the vertical elevation of the viewpoint in degrees. Positive values of elevation correspond to moving above the object; negative values correspond to moving below the object.

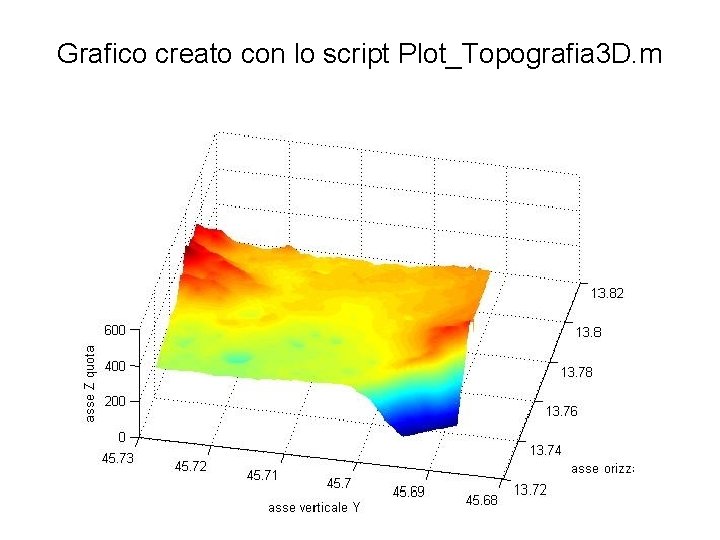
Grafico creato con lo script Plot_Topografia 3 D. m

Grafico delle isolinee della topografia • • %Plot_DTM_isolinea Zmin=200; Zmax=500; step=2; v=Zmin: step: Zmax; sv=size(v); load DTM_ortom_regrid 10 m_WGS 84_HD. mat; %num 2 str converte i numeri in stringhe, altrimenti la concatenazione(di stringhe) non e' possibile • figure('name', ['esempio 2 D isolinee Zmin: ' num 2 str(Zmin) ' Zmax: ' num 2 str(Zmax)]) • %contour rappresenta in grafico le isolinee in 2 D • [C, h]=contour(X 1, Y 1, Z 1, v);

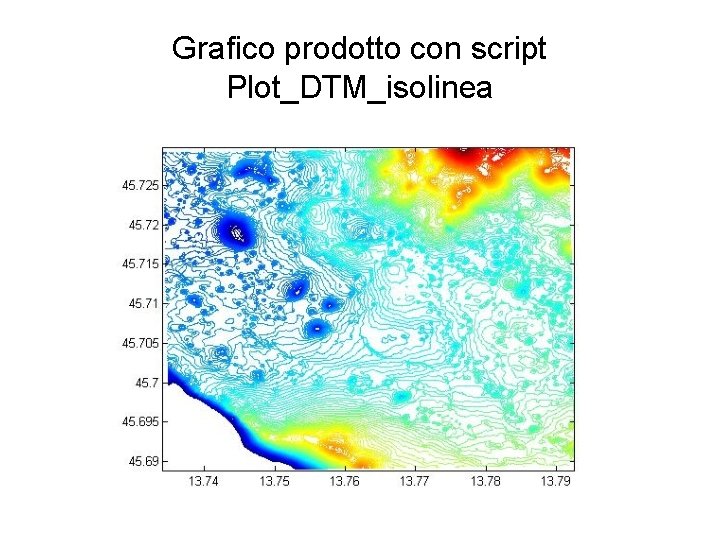
Grafico prodotto con script Plot_DTM_isolinea

Scegli una zona di particolare interesse: aggiungi comando axis. Qui il grafico e’ ristretto su una dolina. • • • • %Plot_DTM_isolinea Zmin=180; Zmax=500; step=2; v=Zmin: step: Zmax; sv=size(v); load DTM_ortom_regrid 10 m_WGS 84_HD. mat; %num 2 str converte i numeri in stringhe, altrimenti la concatenazione(di %stringhe) non e' possibile figure('name', ['esempio 2 D isolinee Zmin: ' num 2 str(Zmin) ' Zmax: ' num 2 str(Zmax)]) %contour rappresenta in grafico le isolinee in 2 D [C, h]=contour(X 1, Y 1, Z 1, v); %axis([xmin xmax ymin ymax]) axis([13. 74 13. 76 45. 715 45. 725]);

Segue l’analisi numerica del DTM. Di seguito utilizziamo il DTM proiettato in coordinate metriche. • Proiezione utilizzata: RDN 2008 fuso 33 • Nome del file: DTM_esercizio 3. MAT

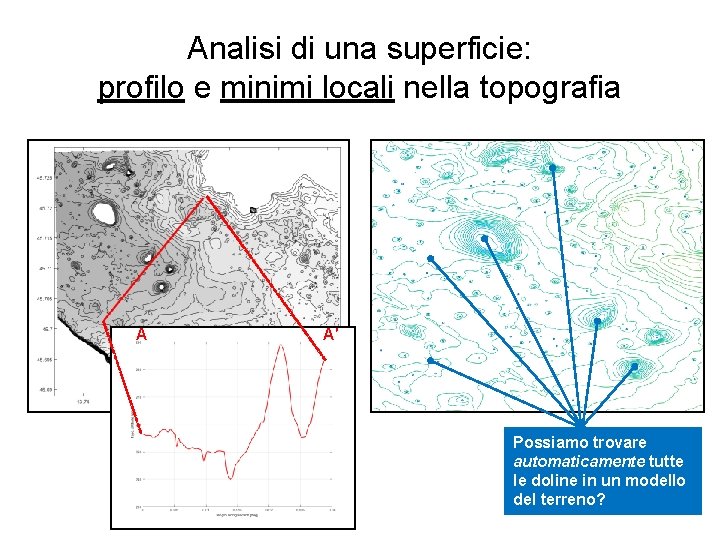
Analisi di una superficie: profilo e minimi locali nella topografia A A′ Possiamo trovare automaticamente tutte le doline in un modello del terreno?

Profilo topografico /1 • • • Vogliamo estrarre il profilo lungo un segmento qualsiasi Il segmento è definito dalle coordinate di inizio e fine Otteniamo le coordinate cliccando sulla figura della mappa load('DTM_esercizio 3'); contourf(X, Y, Z, 25); • carichiamo il DTM, che contiene Z, X, Y • contourf: linee di livello con riempimento, 25 livelli • Questo modello del terreno è in coordinate proiettate, le unità sugli assi sono metri • È presente un valore di altitudine ogni 10 metri, sia lungo x che lungo y • Ovvero: la risoluzione è di 10 metri/pixel

Profilo topografico /2 • • • Vogliamo estrarre il profilo lungo un segmento qualsiasi Il segmento è definito dalle coordinate di inizio e fine Otteniamo le coordinate cliccando sulla figura della mappa Scriviamo una funzione per ottenere questo, utilizzeremo: • • ginput per leggere le coordinate dei punti cliccati da una figura aperta interp 2 per calcolare, interpolando, l’altitudine per ogni punto lungo il profilo – i punti del profilo non coincidono con i nodi della griglia del modello del terreno

Profilo topografico /3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 function [prof. X, prof. Y, prof. L, prof. Z] =. . . Traccia. Profilo(X, Y, Z, passo) % input dei punti contourf(X, Y, Z, 25); hold on [xclick, yclick] = ginput(2); plot(xclick, yclick, 'r', 'Line. Width', 4) % costruzione del segmento del profilo deltax = xclick(2)-xclick(1); deltay = yclick(2)-yclick(1); lunghezza = sqrt((deltax)^2 + (deltay)^2); azi = atan 2((deltay), (deltax)); prof. L = 0: passo: lunghezza; prof. X = xclick(1) + (prof. L * cos(azi)); prof. Y = yclick(1) + (prof. L * sin(azi)); % interpolazione delle quote lungo il profilo prof. Z = interp 2(X, Y, Z, prof. X, prof. Y); end • argomenti input: – X, Y, Z del terreno – passo con cui campioniamo il profilo • ovvero: ogni quanti metri un punto • argomenti output: – prof. X, prof. Y coord. dei punti del profilo – prof. L vettore della distanza lungo il profilo • è 0 : passo : lunghezza del profilo – prof. Z vettore delle quote del profilo

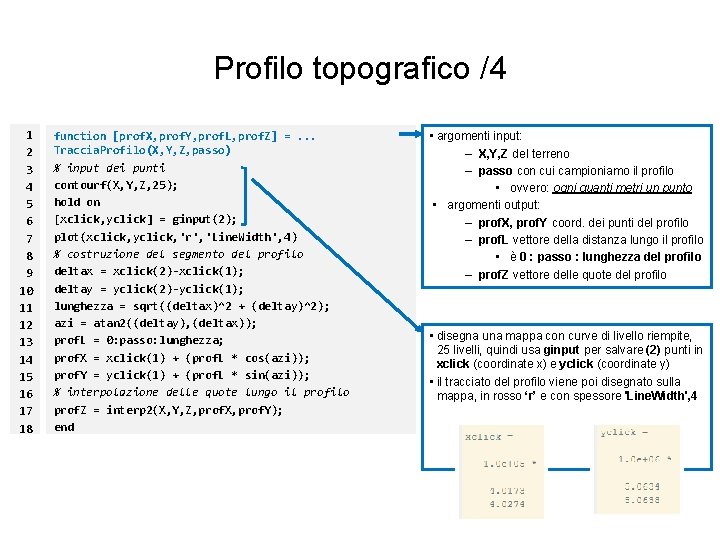
Profilo topografico /4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 function [prof. X, prof. Y, prof. L, prof. Z] =. . . Traccia. Profilo(X, Y, Z, passo) % input dei punti contourf(X, Y, Z, 25); hold on [xclick, yclick] = ginput(2); plot(xclick, yclick, 'r', 'Line. Width', 4) % costruzione del segmento del profilo deltax = xclick(2)-xclick(1); deltay = yclick(2)-yclick(1); lunghezza = sqrt((deltax)^2 + (deltay)^2); azi = atan 2((deltay), (deltax)); prof. L = 0: passo: lunghezza; prof. X = xclick(1) + (prof. L * cos(azi)); prof. Y = yclick(1) + (prof. L * sin(azi)); % interpolazione delle quote lungo il profilo prof. Z = interp 2(X, Y, Z, prof. X, prof. Y); end • argomenti input: – X, Y, Z del terreno – passo con cui campioniamo il profilo • ovvero: ogni quanti metri un punto • argomenti output: – prof. X, prof. Y coord. dei punti del profilo – prof. L vettore della distanza lungo il profilo • è 0 : passo : lunghezza del profilo – prof. Z vettore delle quote del profilo • disegna una mappa con curve di livello riempite, 25 livelli, quindi usa ginput per salvare (2) punti in xclick (coordinate x) e yclick (coordinate y) • il tracciato del profilo viene poi disegnato sulla mappa, in rosso ‘r’ e con spessore 'Line. Width', 4

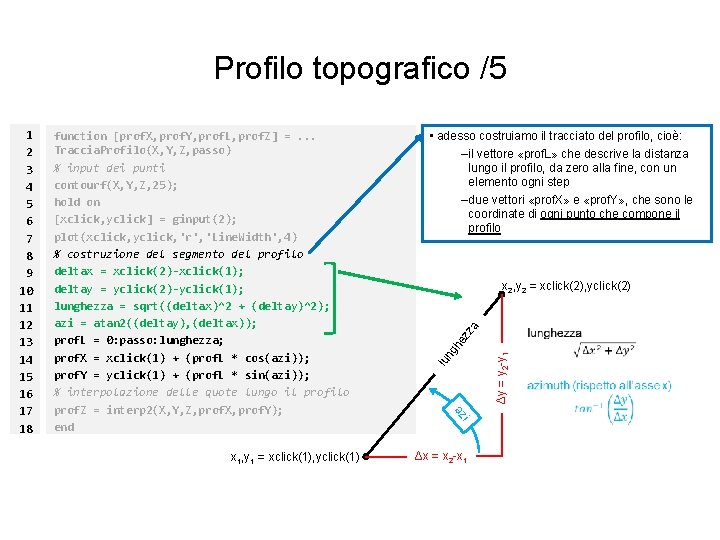
Profilo topografico /5 x 1, y 1 = xclick(1), yclick(1) • adesso costruiamo il tracciato del profilo, cioè: –il vettore «prof. L» che descrive la distanza lungo il profilo, da zero alla fine, con un elemento ogni step –due vettori «prof. X» e «prof. Y» , che sono le coordinate di ogni punto che compone il profilo lu Δy = y 2 -y 1 ng he zz a x 2, y 2 = xclick(2), yclick(2) i function [prof. X, prof. Y, prof. L, prof. Z] =. . . Traccia. Profilo(X, Y, Z, passo) % input dei punti contourf(X, Y, Z, 25); hold on [xclick, yclick] = ginput(2); plot(xclick, yclick, 'r', 'Line. Width', 4) % costruzione del segmento del profilo deltax = xclick(2)-xclick(1); deltay = yclick(2)-yclick(1); lunghezza = sqrt((deltax)^2 + (deltay)^2); azi = atan 2((deltay), (deltax)); prof. L = 0: passo: lunghezza; prof. X = xclick(1) + (prof. L * cos(azi)); prof. Y = yclick(1) + (prof. L * sin(azi)); % interpolazione delle quote lungo il profilo prof. Z = interp 2(X, Y, Z, prof. X, prof. Y); end az 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Δx = x 2 -x 1

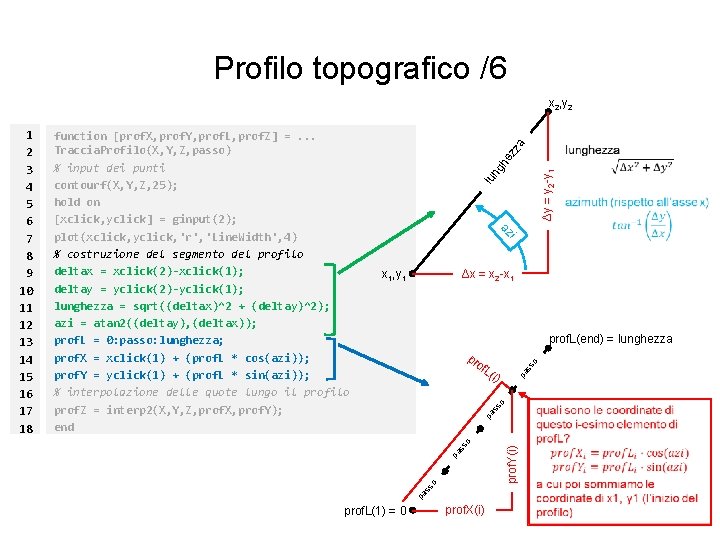
Profilo topografico /6 he z Δy = y 2 -y 1 ng lu Δx = x 2 -x 1 x 1, y 1 of prof. X(i) prof. Y(i) pa ss pa s so pa s prof. L(1) = 0 i) o L( pa s pr so prof. L(end) = lunghezza so function [prof. X, prof. Y, prof. L, prof. Z] =. . . Traccia. Profilo(X, Y, Z, passo) % input dei punti contourf(X, Y, Z, 25); hold on [xclick, yclick] = ginput(2); plot(xclick, yclick, 'r', 'Line. Width', 4) % costruzione del segmento del profilo deltax = xclick(2)-xclick(1); deltay = yclick(2)-yclick(1); lunghezza = sqrt((deltax)^2 + (deltay)^2); azi = atan 2((deltay), (deltax)); prof. L = 0: passo: lunghezza; prof. X = xclick(1) + (prof. L * cos(azi)); prof. Y = yclick(1) + (prof. L * sin(azi)); % interpolazione delle quote lungo il profilo prof. Z = interp 2(X, Y, Z, prof. X, prof. Y); end i az 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 za x 2, y 2

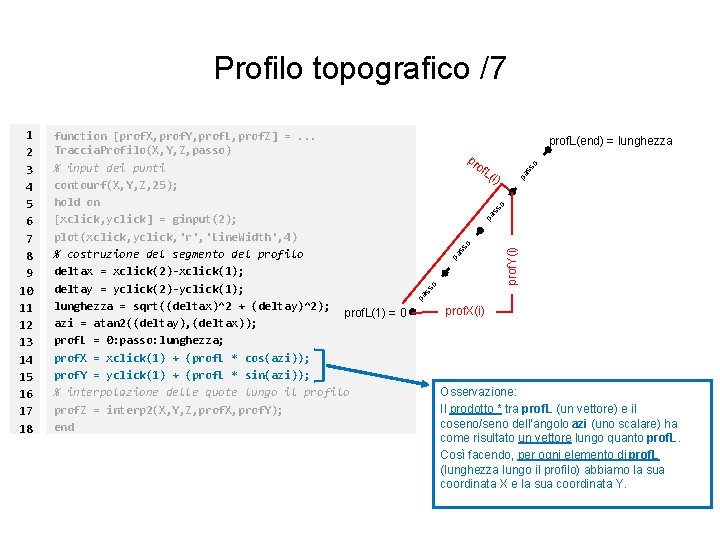
Profilo topografico /7 of i) prof. Y(i) pa ss o L( pa pr ss o prof. L(end) = lunghezza so function [prof. X, prof. Y, prof. L, prof. Z] =. . . Traccia. Profilo(X, Y, Z, passo) % input dei punti contourf(X, Y, Z, 25); hold on [xclick, yclick] = ginput(2); plot(xclick, yclick, 'r', 'Line. Width', 4) % costruzione del segmento del profilo deltax = xclick(2)-xclick(1); deltay = yclick(2)-yclick(1); lunghezza = sqrt((deltax)^2 + (deltay)^2); prof. L(1) = 0 azi = atan 2((deltay), (deltax)); prof. L = 0: passo: lunghezza; prof. X = xclick(1) + (prof. L * cos(azi)); prof. Y = yclick(1) + (prof. L * sin(azi)); % interpolazione delle quote lungo il profilo prof. Z = interp 2(X, Y, Z, prof. X, prof. Y); end pa s 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 prof. X(i) Osservazione: Il prodotto * tra prof. L (un vettore) e il coseno/seno dell’angolo azi (uno scalare) ha come risultato un vettore lungo quanto prof. L. Così facendo, per ogni elemento di prof. L (lunghezza lungo il profilo) abbiamo la sua coordinata X e la sua coordinata Y.

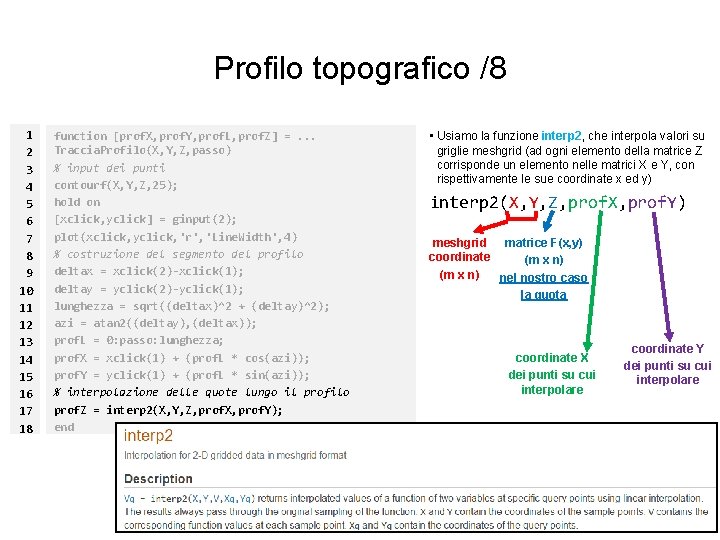
Profilo topografico /8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 function [prof. X, prof. Y, prof. L, prof. Z] =. . . Traccia. Profilo(X, Y, Z, passo) % input dei punti contourf(X, Y, Z, 25); hold on [xclick, yclick] = ginput(2); plot(xclick, yclick, 'r', 'Line. Width', 4) % costruzione del segmento del profilo deltax = xclick(2)-xclick(1); deltay = yclick(2)-yclick(1); lunghezza = sqrt((deltax)^2 + (deltay)^2); azi = atan 2((deltay), (deltax)); prof. L = 0: passo: lunghezza; prof. X = xclick(1) + (prof. L * cos(azi)); prof. Y = yclick(1) + (prof. L * sin(azi)); % interpolazione delle quote lungo il profilo prof. Z = interp 2(X, Y, Z, prof. X, prof. Y); end • Usiamo la funzione interp 2, che interpola valori su griglie meshgrid (ad ogni elemento della matrice Z corrisponde un elemento nelle matrici X e Y, con rispettivamente le sue coordinate x ed y) interp 2(X, Y, Z, prof. X, prof. Y) meshgrid matrice F(x, y) coordinate (m x n) nel nostro caso la quota coordinate X dei punti su cui interpolare coordinate Y dei punti su cui interpolare

Profilo topografico /9 % chiudi finestre aperte da vecchie figure % ed elimina eventuali variabili già esistenti close all clear variables % carica la topografia (X, Y, Z) load('DTM_esercizio 3'); % chiamata alla funzione Traccia. Profilo [profilo. X, profilo. Y, profilo. Dist, profilo. Quota] =. . . Traccia. Profilo(X, Y, Z, 5); % figura: mappa Assi. Mappa = subplot(3, 1, [1 2]); contourf(Assi. Mappa, X, Y, Z, 25); hold on; plot(Assi. Mappa, profilo. X, profilo. Y, 'r', 'Line. Width', 4); % figura: profilo Assi. Profilo = subplot(3, 1, 3); plot(Assi. Profilo, profilo. Dist, profilo. Quota, 'r'); • Con uno script, come quello qui lato: 1. Carichiamo il modello del terreno 2. Chiamiamo la funzione Traccia. Profilo 3. La funzione ci restituisce: – il tracciato del profilo in coordinate – i punti lungo il profilo – la quota in ciascuno dei punti lungo il profilo 4. Creiamo una figura con due subplot su tre righe: – sopra: la mappa con i contour (occupa due caselle subplot) e il tracciato del profilo – sotto: il profilo (in x la distanza, in y la quota)

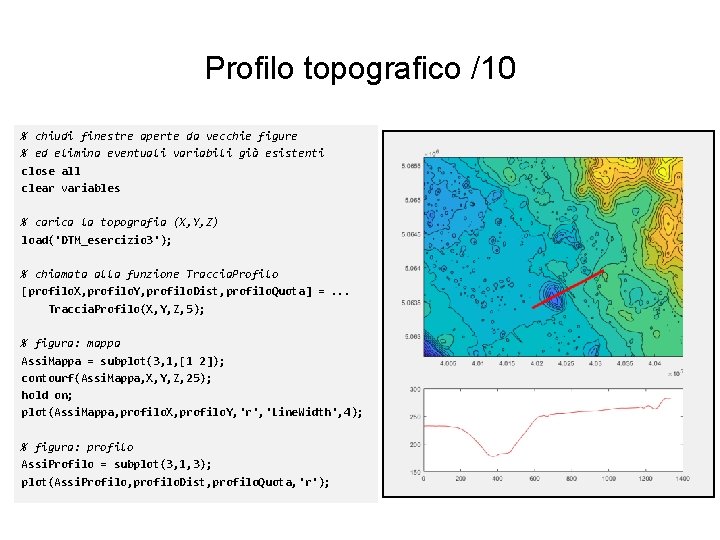
Profilo topografico /10 % chiudi finestre aperte da vecchie figure % ed elimina eventuali variabili già esistenti close all clear variables % carica la topografia (X, Y, Z) load('DTM_esercizio 3'); % chiamata alla funzione Traccia. Profilo [profilo. X, profilo. Y, profilo. Dist, profilo. Quota] =. . . Traccia. Profilo(X, Y, Z, 5); % figura: mappa Assi. Mappa = subplot(3, 1, [1 2]); contourf(Assi. Mappa, X, Y, Z, 25); hold on; plot(Assi. Mappa, profilo. X, profilo. Y, 'r', 'Line. Width', 4); % figura: profilo Assi. Profilo = subplot(3, 1, 3); plot(Assi. Profilo, profilo. Dist, profilo. Quota, 'r');

Ricerca dei minimi locali /1 Vogliamo individuare i minimi locali su una superficie. Nello specifico, le doline in un modello digitale del terreno (DTM) in zona carsica. Le condizioni sono le seguenti: 1. La superficie è molto estesa e i minimi sono numerosi 2. La superficie è campionata regolarmente, in punti discreti (non è una funzione analitica) 3. È presente del rumore, ovvero dei minimi locali che non sono il nostro obiettivo. Esempio: piccole asperità nel terreno.

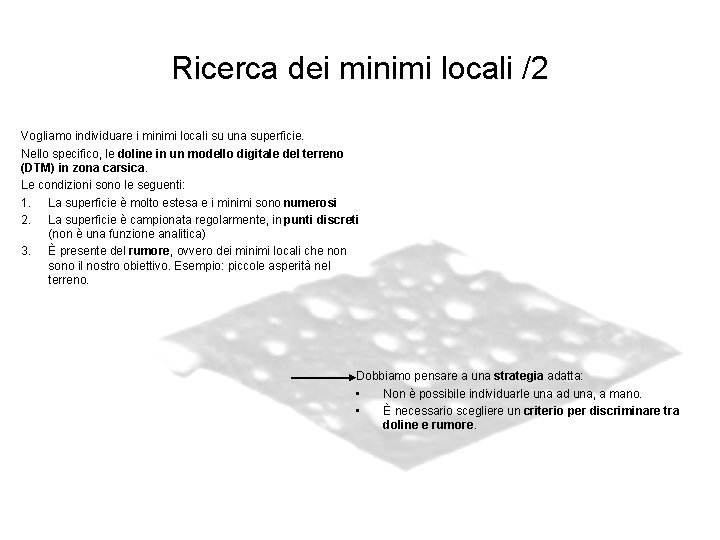
Ricerca dei minimi locali /2 Vogliamo individuare i minimi locali su una superficie. Nello specifico, le doline in un modello digitale del terreno (DTM) in zona carsica. Le condizioni sono le seguenti: 1. La superficie è molto estesa e i minimi sono numerosi 2. La superficie è campionata regolarmente, in punti discreti (non è una funzione analitica) 3. È presente del rumore, ovvero dei minimi locali che non sono il nostro obiettivo. Esempio: piccole asperità nel terreno. Dobbiamo pensare a una strategia adatta: • Non è possibile individuarle una ad una, a mano. • È necessario scegliere un criterio per discriminare tra doline e rumore.

Ricerca dei minimi locali /3 • con det. Hess>0 : molto rumore matrice Hessiana Per la dimostrazione, vedere: http: //calvino. polito. it/~taise/Esercizi %202006/2006 -05 -25%20%20 Appunti%20 -%20 Hessiana. pdf load('DTM_esercizio 3. mat') [gx, gy] = gradient(Z); [gxx, ~] = gradient(gx); [gxy, gyy] = gradient(gy); det. Hess = gxx. *gyy - gxy. ^2; minimi=find(and(det. Hess>0, gxx>0)); minimi. X = X(minimi); minimi. Y = Y(minimi); con det. Hess>2 : meno rumore

Ricerca dei minimi locali /4 Disegniamo i punti trovati su una mappa contourf: contourf(X, Y, Z, 50); hold on; scatter(minimi. TEST_X, minimi. TEST_Y, 6, 'r'); % « 6» indica la dimensione dei punti, ‘r’ il colore rosso Problemi: • Non sempre i punti trovati corrispondono al nostro obiettivo (doline) • Spesso sono presenti più punti per ciascuna dolina (fondo piatto)

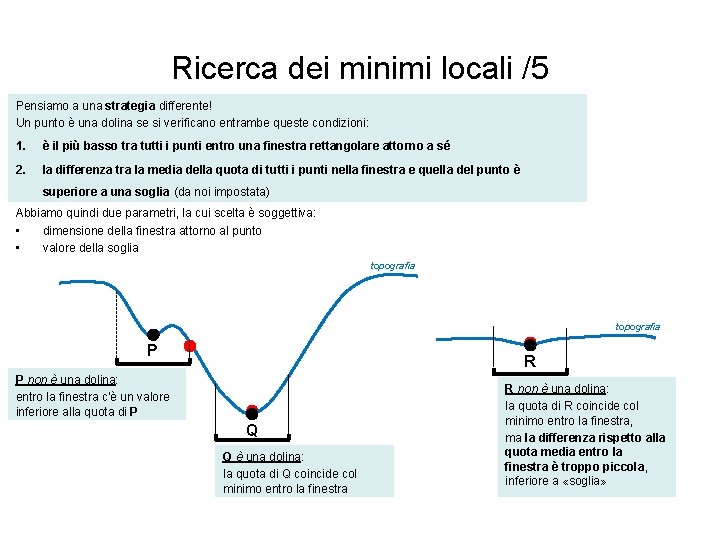
Ricerca dei minimi locali /5 Pensiamo a una strategia differente! Un punto è una dolina se si verificano entrambe queste condizioni: 1. è il più basso tra tutti i punti entro una finestra rettangolare attorno a sé 2. la differenza tra la media della quota di tutti i punti nella finestra e quella del punto è superiore a una soglia (da noi impostata) Abbiamo quindi due parametri, la cui scelta è soggettiva: • dimensione della finestra attorno al punto • valore della soglia topografia P R P non è una dolina: entro la finestra c’è un valore inferiore alla quota di P Q Q è una dolina: la quota di Q coincide col minimo entro la finestra R non è una dolina: la quota di R coincide col minimo entro la finestra, ma la differenza rispetto alla quota media entro la finestra è troppo piccola, inferiore a «soglia»

Ricerca dei minimi locali /6 Scriviamo quanto appena descritto come una funzione. Argomenti in input: A matrice delle quote, finestra dimensione della finestra, soglia valore della soglia Argomenti in output: U, V indici degli elementi che sono doline (grazie ad X e Y poi li tradurremo in coordinate) function [U, V] = Cerca. Doline(A, finestra, soglia) D = zeros(size(A)); for u=1+finestra: size(A, 1)-finestra for v=1+finestra: size(A, 2)-finestra fmin = min(A(u-finestra: u+finestra, v-finestra: v+finestra))); fmed = mean(A(u-finestra: u+finestra, v-finestra: v+finestra))); if A(u, v)==fmin && fmed-fmin>= soglia D(u, v) = 1; end end [U, V] = find(D==1); end finestra = numero di elementi di cui ci allontaniamo dall’elemento (u, v), in ciascuna direzione Osservazione: il ciclo for evita i bordi della nostra matrice, inizia a una finestra di distanza dal bordo. Vedi: le due righe del ciclo for.

Ricerca dei minimi locali /7 Chiamiamo «Cerca. Doline» in uno script e disegniamo i risultati su una mappa. load('DTM_esercizio 3'); [U, V] = Cerca. Doline(Z, 5, 0. 5); doline. X = X(1, V); doline. Y = Y(U, 1); contour(X, Y, Z, 50); hold on; scatter(doline. X, doline. Y, 6, 'r'); • • finestra = 5, c’è un elemento ogni 10 metri, quindi 5 x 10 x 2 = 100 metri soglia = 0. 5 m estraiamo dalla prima riga di X e dalla prima colonna di Y le coordinate che corrispondono a ciascun punto definito da U e V Sembra funzionare meglio. Cosa accade variando i due parametri?

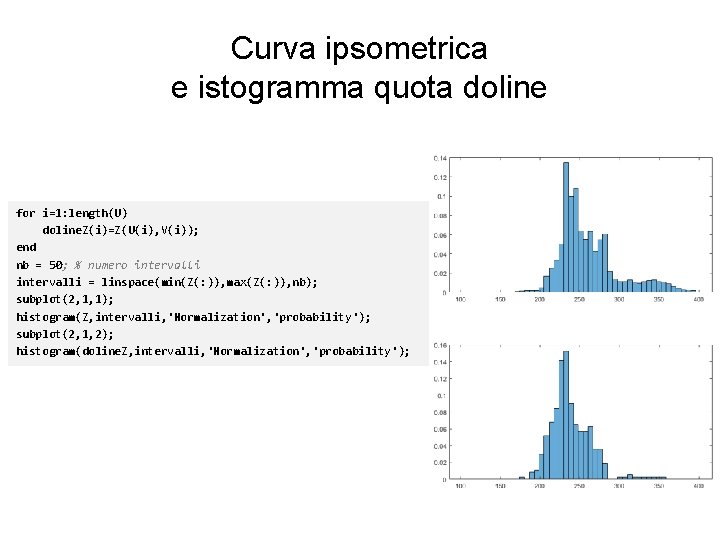
Curva ipsometrica e istogramma quota doline for i=1: length(U) doline. Z(i)=Z(U(i), V(i)); end nb = 50; % numero intervalli = linspace(min(Z(: )), max(Z(: )), nb); subplot(2, 1, 1); histogram(Z, intervalli, 'Normalization', 'probability'); subplot(2, 1, 2); histogram(doline. Z, intervalli, 'Normalization', 'probability');