Plane Wave Propagation in Lossy Media Asst Prof

Lossy Media A lossy dielectric is a medium in which an EM wave loses

Lossy Media In a lossless dielectric medium, the relative permittivity εr is real, For

Loss Tangent is called the loss tangent › The complex permittivity can be written

Helmholtz’s equation By replacing k with kc, all the previous results derived for lossless

Helmholtz’s equation γ is known as the complex propagation constant › solutions with the

Complex Propagation The general form of a plane wave in a lossy medium is

Good Conductor Loss tangent for a good conductor is;

Good Conductor In a good conductor, the intrinsic impedance ηc is a complex number,

Good Conductor Phase velocity and wavelength

Good Conductor H and E inside a good conductor

Good Conductor Skin Depth › Because of the attenuation constant α, the wave amplitude

Skin Depth For copper σ = 5. 8 × 107 S/m and μr =1

Low Loss Dielectrics For a low loss dielectric loss tangent satisfies

Low Loss Dielectrics A skin depth δ can be similarly defined as in the

Example 1 The electric field intensity of a linearly polarised uniform plane wave propagating

Determine the attenuation constant, intrinsic impedance, phase velocity, wavelength, and skin depth.

Write expressions for H(z, t) and E(z, t).

Find the distance z 1 at which the amplitude of the electric field

Compute the skin depth at a frequency of 1 GHz.

find the power densities at distances of skin depth z = δ and

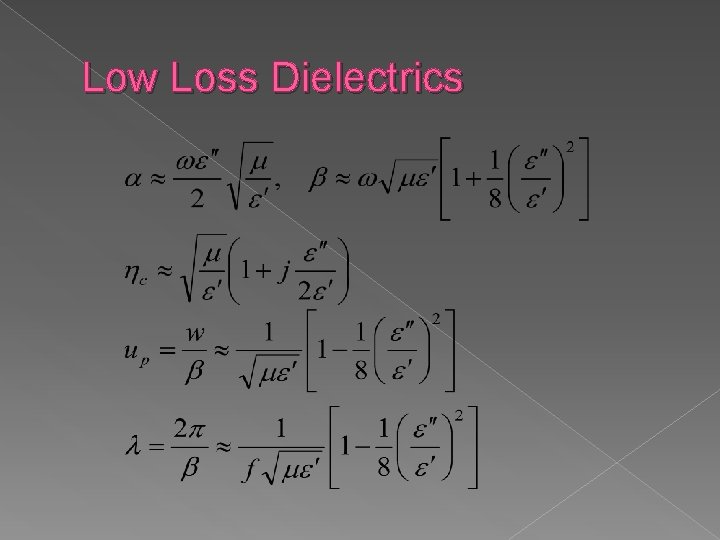
Slides: 32

Download presentation

Plane Wave Propagation in Lossy Media Asst. Prof. Dr. Özgür Tamer

Lossy Media A lossy dielectric is a medium in which an EM wave loses power as it propagates due to poor conduction. A lossy dielectric is a partially conducting medium

Lossy Media In a lossless dielectric medium, the relative permittivity εr is real, For non-magnetic materials, the relative permeability μr =1 For lossy media permittivity is a complex number

Lossy Media In a lossy medium

Loss Tangent is called the loss tangent › The complex permittivity can be written as

Loss Tangent Current Terms

Helmholtz’s equation By replacing k with kc, all the previous results derived for lossless media are applicable to lossy media. But since kc is a complex number, the plane wave will experience loss when it propagates.

Helmholtz’s equation γ is known as the complex propagation constant › solutions with the +α constant have been discarded as they imply waves with increasing amplitudes which is impossible

Complex Propagation

Complex Propagation The general form of a plane wave in a lossy medium is

Complex Propagation

Good Conductor Loss tangent for a good conductor is;

Good Conductor In a good conductor, the intrinsic impedance ηc is a complex number, meaning that the electric and magnetic fields are not in phase as in the case of a lossless medium.

Good Conductor Phase velocity and wavelength

Good Conductor H and E inside a good conductor

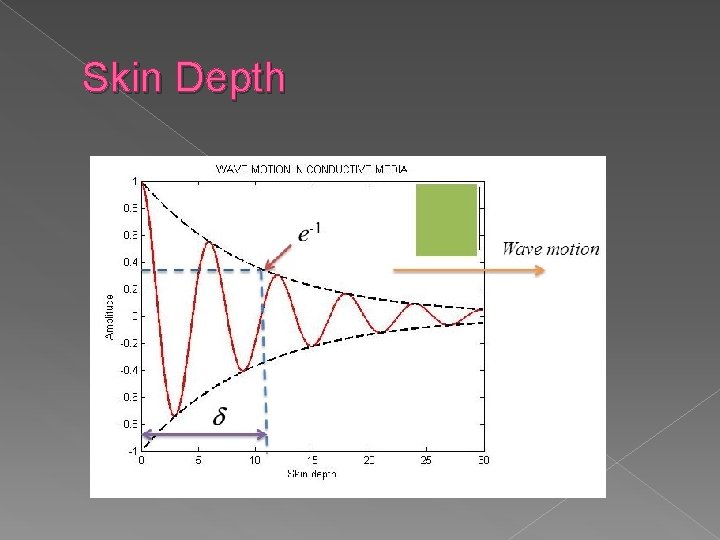
Good Conductor Skin Depth › Because of the attenuation constant α, the wave amplitude becomes smaller when it propagates through a good conductor. › amplitude of a travelling plane wave decreases by a factor of e-1 = 0. 368 = 36. 8% is called the skin depth

Skin Depth

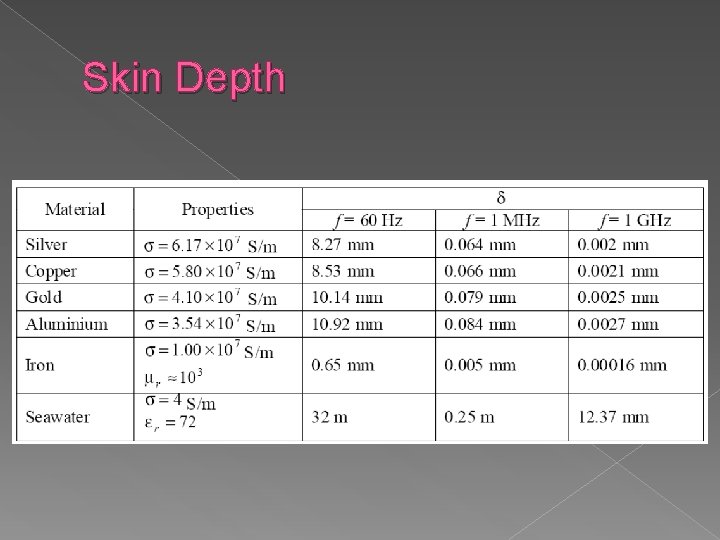
Skin Depth For copper σ = 5. 8 × 107 S/m and μr =1

Skin Depth

Low Loss Dielectrics For a low loss dielectric loss tangent satisfies

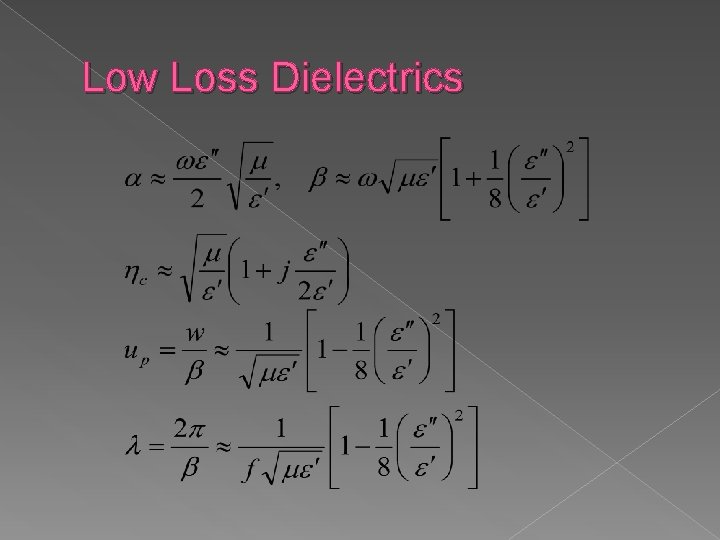
Low Loss Dielectrics

Low Loss Dielectrics A skin depth δ can be similarly defined as in the good conductor case:

Example 1 The electric field intensity of a linearly polarised uniform plane wave propagating in the +z direction in seawater is E = x 100 cos(107 πt) at z=0. The constitutive parameters of seawater are εr = 72, μr = 1, and σ = 4 S/m.

Determine the attenuation constant, intrinsic impedance, phase velocity, wavelength, and skin depth.

Write expressions for H(z, t) and E(z, t).

Find the distance z 1 at which the amplitude of the electric field is 1% of its value at z = 0.

Compute the skin depth at a frequency of 1 GHz.

find the power densities at distances of skin depth z = δ and z = 0.