Plane of symmetry Axis of symmetry Symbol for

Plane of symmetry Axis of symmetry

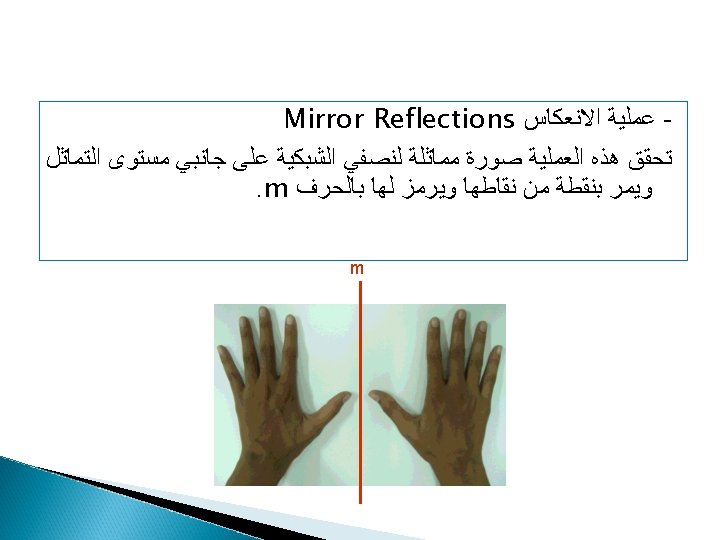
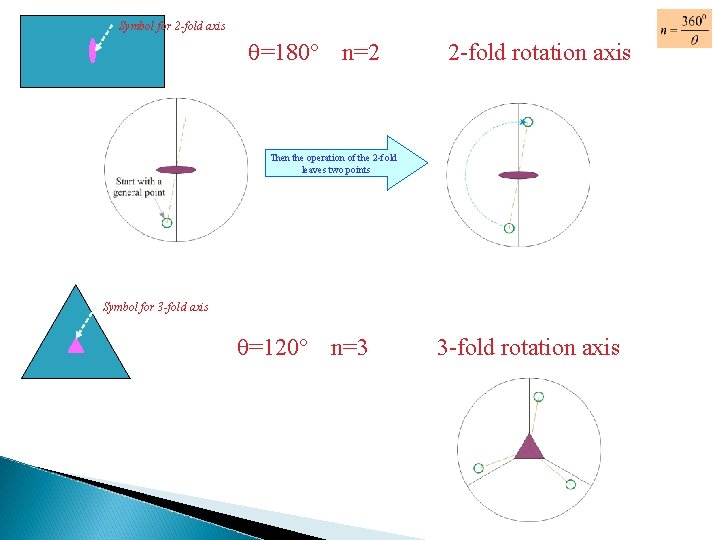
Symbol for 2 -fold axis =180 n=2 2 -fold rotation axis Then the operation of the 2 -fold leaves two points Symbol for 3 -fold axis =120 n=3 3 -fold rotation axis

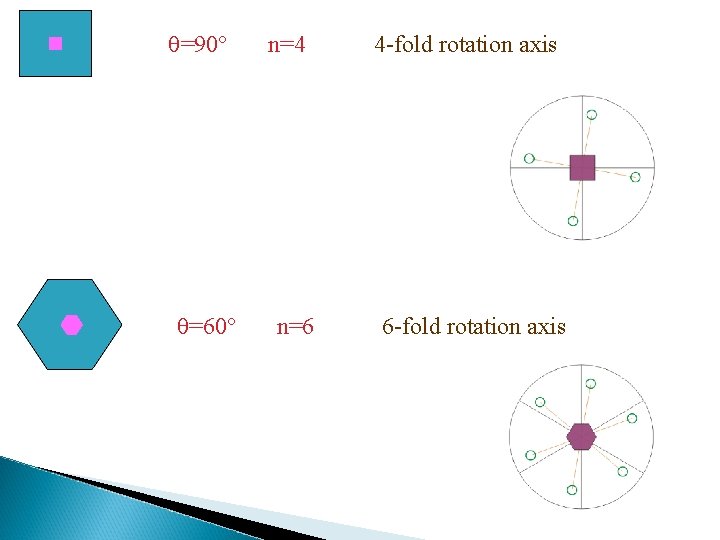
=90 =60 n=4 n=6 4 -fold rotation axis 6 -fold rotation axis

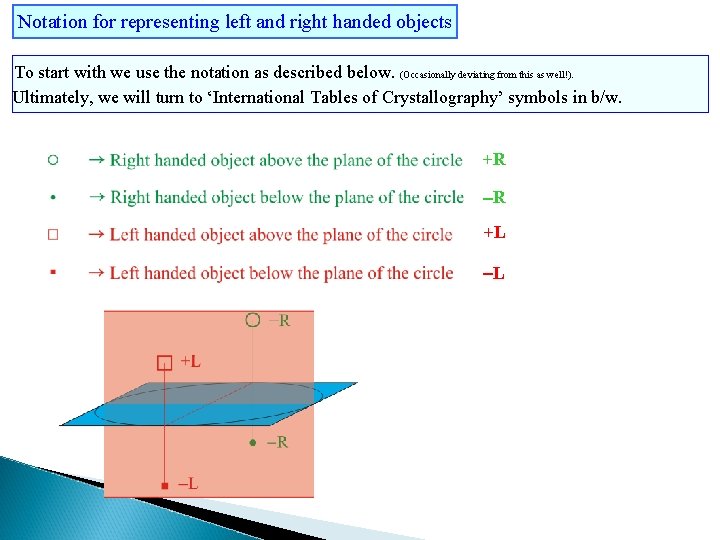
Notation for representing left and right handed objects To start with we use the notation as described below. (Occasionally deviating from this as well!). Ultimately, we will turn to ‘International Tables of Crystallography’ symbols in b/w. +R R +L L

Translation The translation symmetry operator (t) moves an point or an object by a displacement t or a q distance t. A periodic array of points or objects is said to posses translational symmetry. q Translational symmetry could be in 2 D or 3 D (or in general n. D). q If we have translational symmetry in a pattern then instead of describing the entire pattern q we can describe the ‘repeat unit’ and the translation vector(s). t

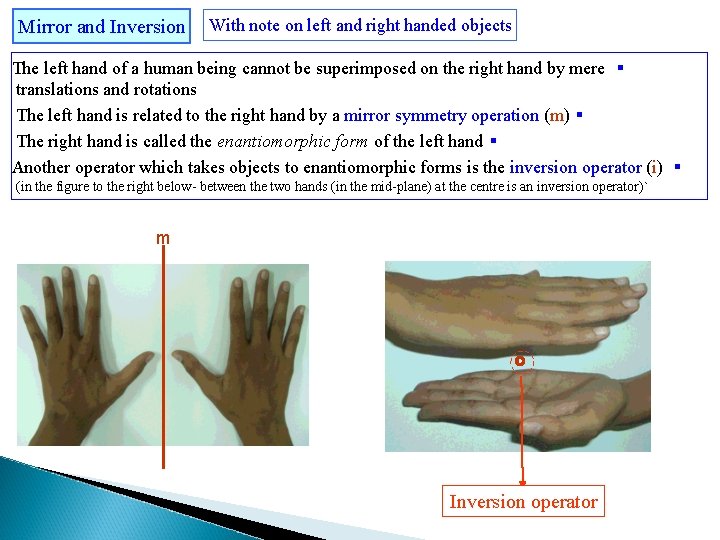
Mirror and Inversion With note on left and right handed objects The left hand of a human being cannot be superimposed on the right hand by mere § translations and rotations The left hand is related to the right hand by a mirror symmetry operation (m) § The right hand is called the enantiomorphic form of the left hand § Another operator which takes objects to enantiomorphic forms is the inversion operator (i) § (in the figure to the right below- between the two hands (in the mid-plane) at the centre is an inversion operator)` m Inversion operator

Rotation Axis Rotation axis rotates a general point (and hence entire space) around the axis by a certain q angle On repeated operation (rotation) the ‘starting’ point leaves a set of ‘identity-points*’ before q coming into coincidence with itself. As we are interested mainly with crystals, we are interested in those rotations axes which q are compatible with translational symmetry → these are the (1), 2, 3, 4, 6 – fold axis. If an object come into self-coincidence through smallest non-zero rotation angle of then it is said to have an n-fold rotation axis where: The rotations compatible with translational symmetry are (1, 2, 3, 4, 6) Click here for proof Crystals can only have 1, 2, 3, 4 or 6 fold symmetry * explained in an upcoming slide

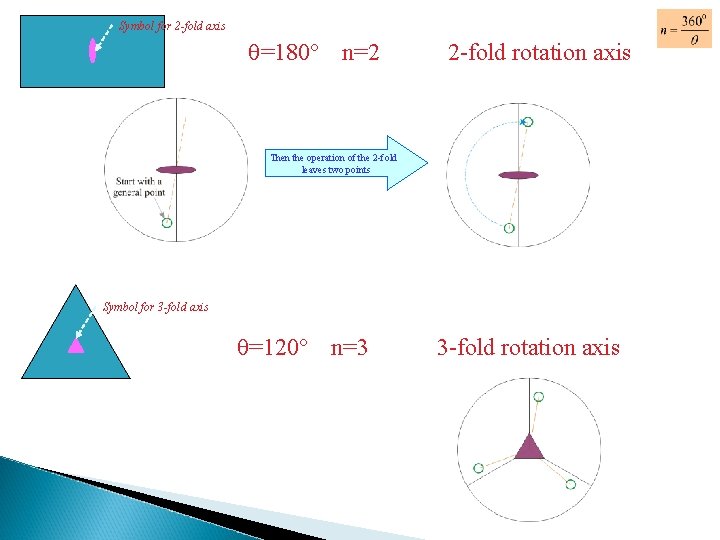
Symbol for 2 -fold axis =180 n=2 2 -fold rotation axis Then the operation of the 2 -fold leaves two points Symbol for 3 -fold axis =120 n=3 3 -fold rotation axis

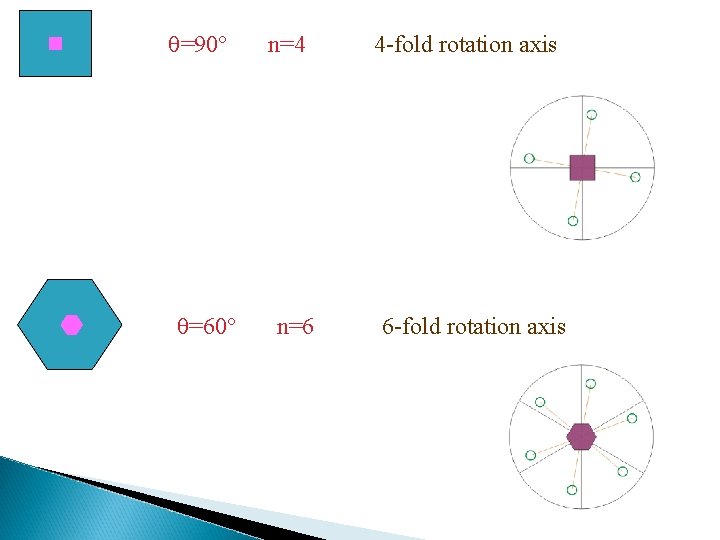
=90 =60 n=4 n=6 4 -fold rotation axis 6 -fold rotation axis

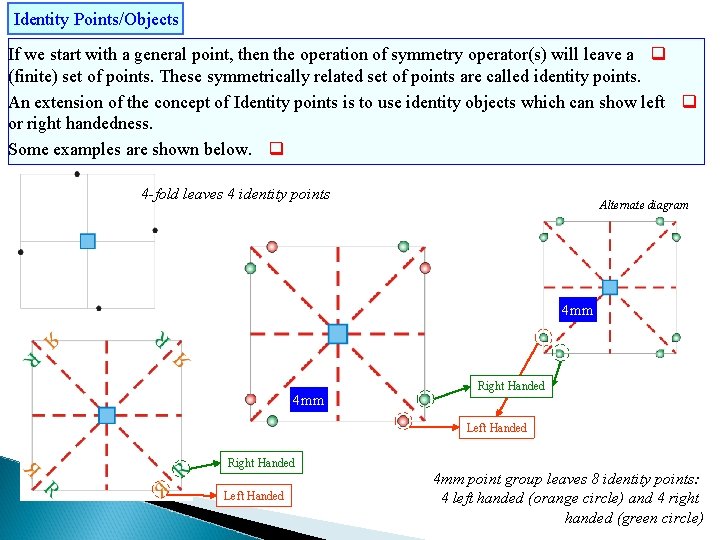
Identity Points/Objects If we start with a general point, then the operation of symmetry operator(s) will leave a q (finite) set of points. These symmetrically related set of points are called identity points. An extension of the concept of Identity points is to use identity objects which can show left q or right handedness. Some examples are shown below. q 4 -fold leaves 4 identity points Alternate diagram 4 mm Right Handed Left Handed 4 mm point group leaves 8 identity points: 4 left handed (orange circle) and 4 right handed (green circle)

Compound Symmetry Operators Translation, mirror, inversion & rotation are simple symmetry operators which we had q considered Roto-inversion and Roto-reflection are compound symmetry operators which do not q involve translation → both these take left handed objects to right handed form For generating point groups (to be considered later) one of the two operators is sufficient and hence we will consider roto-inversion only in future. Glide reflection and Screw are compound symmetry operators involving translation q → Only Glide reflection takes left handed objects to right handed form It is important to note in these operations the compound operator acts before leaving a q identity-point (i. e. Roto-inversion is NOT rotation followed by a inversion). In some cases these compound operators can be broken down into a combination of two q operators. In a combination (unlike a compound) the individual operators express themselves fully – i. e. the first operator acts first and then the second acts on the result of the first operation.

Roto-inversion A roto-inversion operator rotates a point/object and then inverts it (inversion operation) in q one go. A left handed object will be taken to its right handed form by the operation. q We will only consider 1, 2, 3, 4, 6 - fold rotations (crystallographic) as a part of the roto- q inversion operation. Roto-inversion operations Compatible with translational symmetry

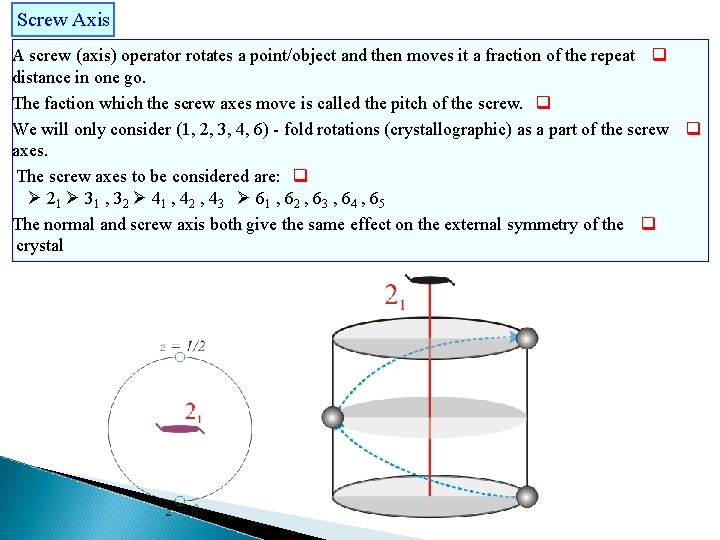
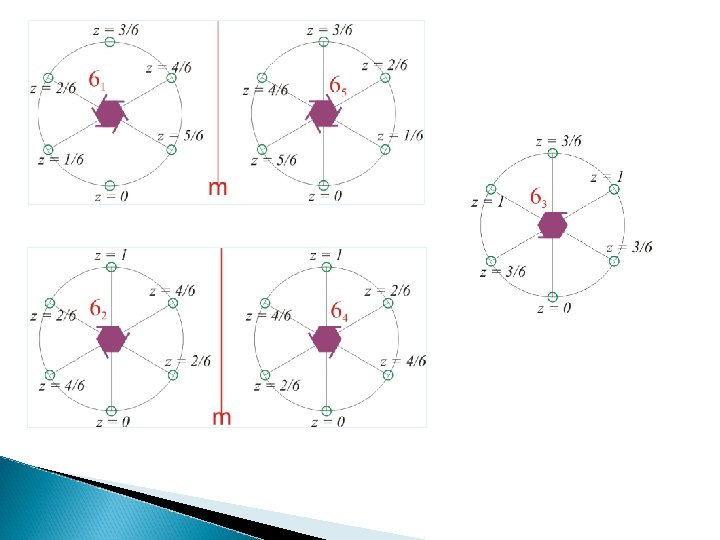
Screw Axis A screw (axis) operator rotates a point/object and then moves it a fraction of the repeat q distance in one go. The faction which the screw axes move is called the pitch of the screw. q We will only consider (1, 2, 3, 4, 6) - fold rotations (crystallographic) as a part of the screw q axes. The screw axes to be considered are: q 21 31 , 32 41 , 42 , 43 61 , 62 , 63 , 64 , 65 The normal and screw axis both give the same effect on the external symmetry of the q crystal

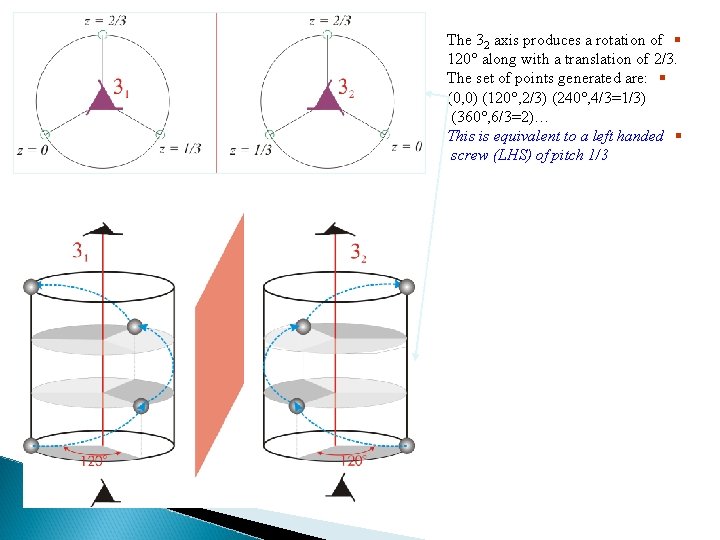
The 32 axis produces a rotation of § 120 along with a translation of 2/3. The set of points generated are: § (0, 0) (120 , 2/3) (240 , 4/3=1/3) (360 , 6/3=2)… This is equivalent to a left handed § screw (LHS) of pitch 1/3

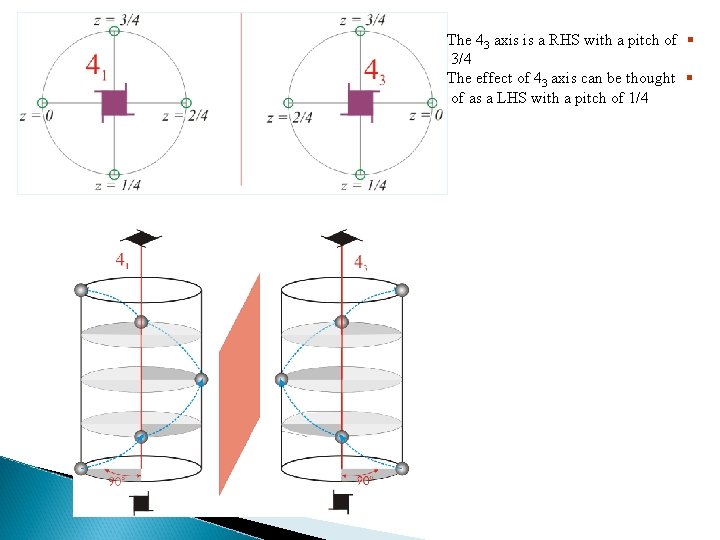
The 43 axis is a RHS with a pitch of § 3/4 The effect of 43 axis can be thought § of as a LHS with a pitch of 1/4

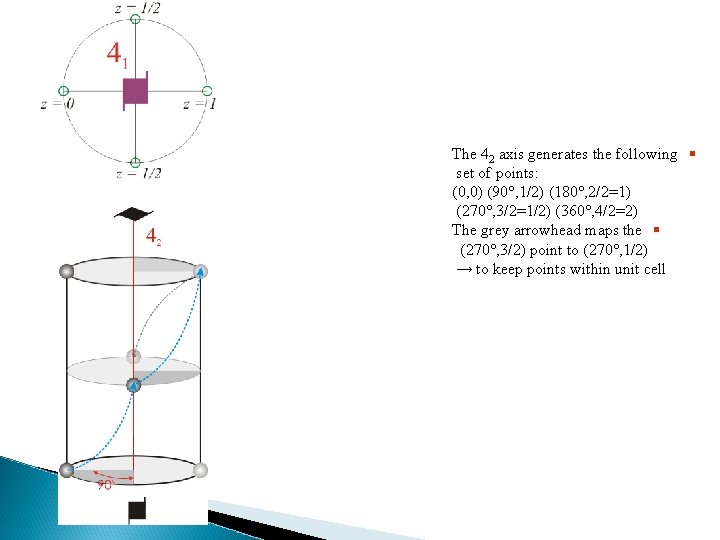
The 42 axis generates the following § set of points: (0, 0) (90 , 1/2) (180 , 2/2=1) (270 , 3/2=1/2) (360 , 4/2=2) The grey arrowhead maps the § (270 , 3/2) point to (270 , 1/2) → to keep points within unit cell

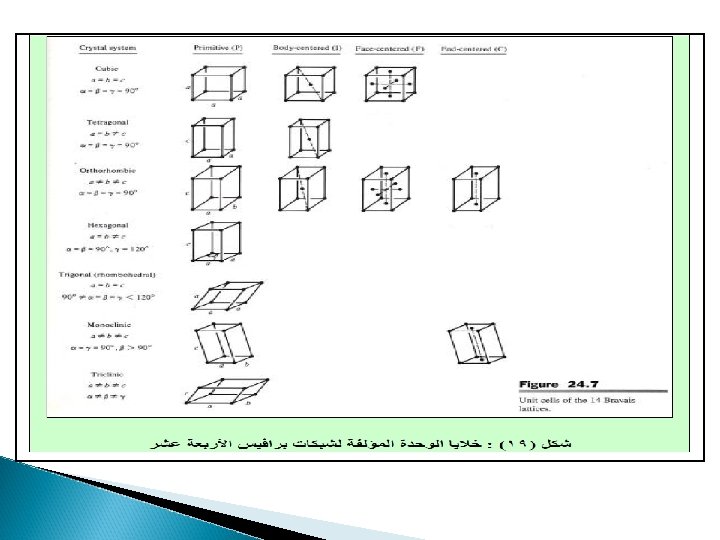
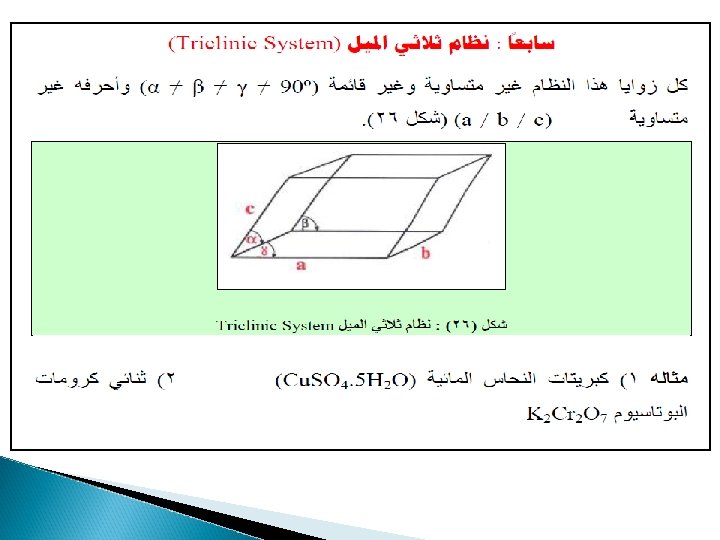
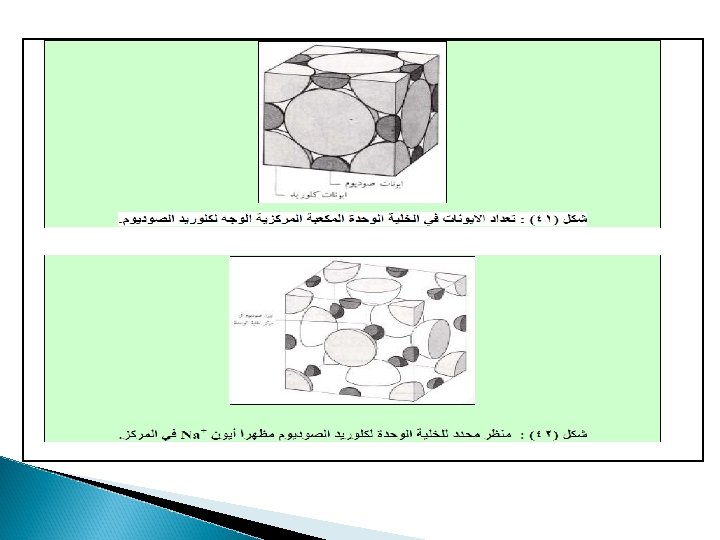
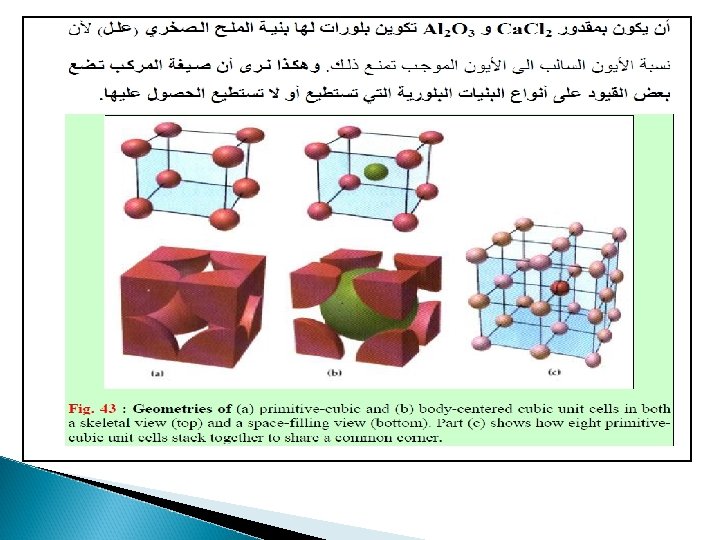
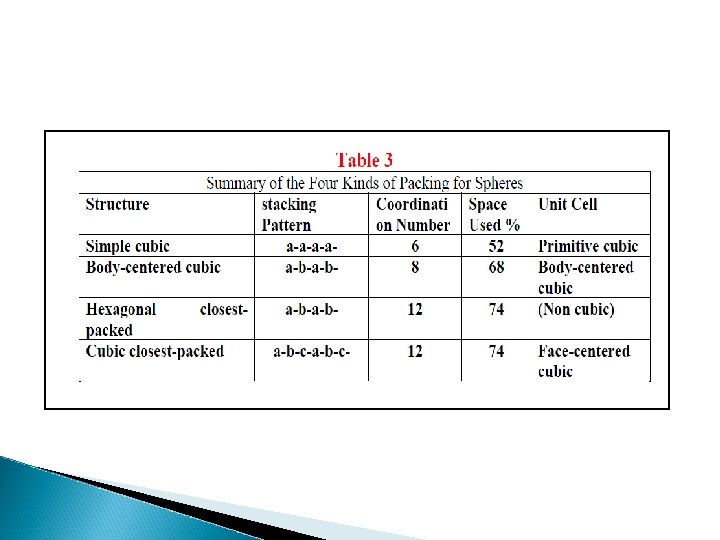
And now for something completely different. . .