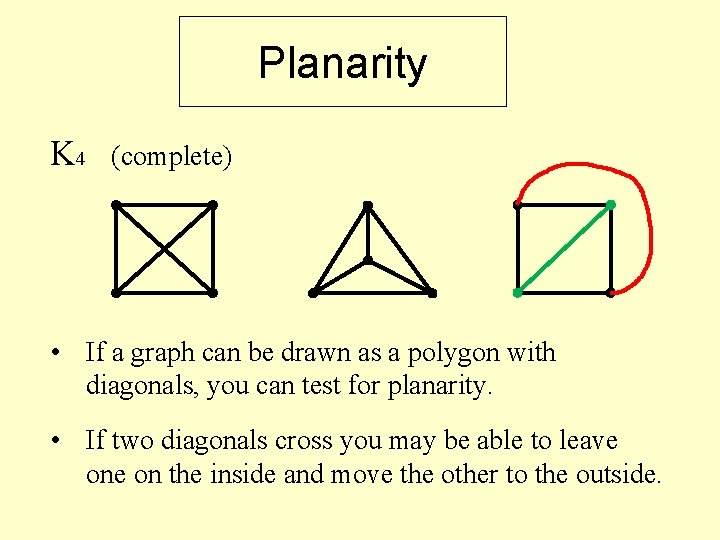
Planarity K 4 complete If a graph can
- Slides: 11

Planarity K 4 (complete) • If a graph can be drawn as a polygon with diagonals, you can test for planarity. • If two diagonals cross you may be able to leave on the inside and move the other to the outside.

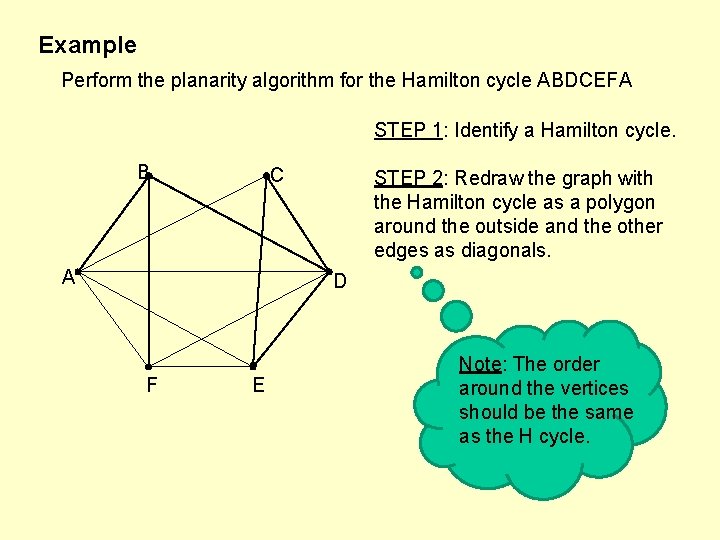
Example Perform the planarity algorithm for the Hamilton cycle ABDCEFA STEP 1: Identify a Hamilton cycle. B C A STEP 2: Redraw the graph with the Hamilton cycle as a polygon around the outside and the other edges as diagonals. D F E Note: The order around the vertices should be the same as the H cycle.

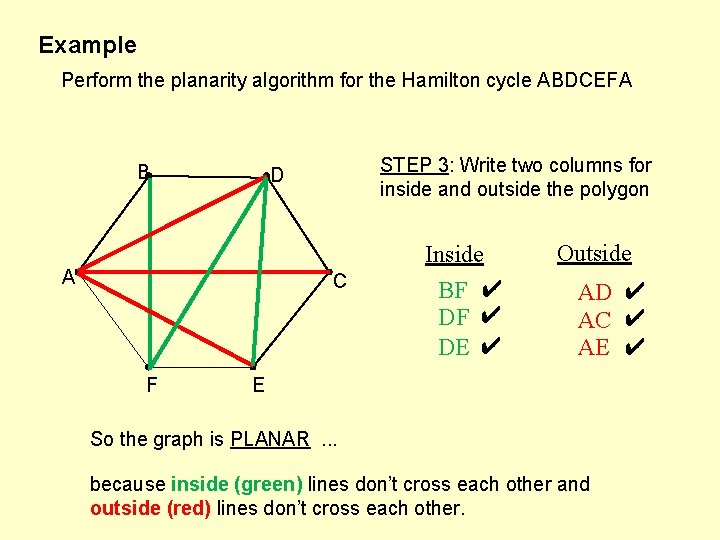
Example Perform the planarity algorithm for the Hamilton cycle ABDCEFA B STEP 3: Write two columns for inside and outside the polygon D A C F Inside BF ✔ DE ✔ Outside AD ✔ AC ✔ AE ✔ E So the graph is PLANAR. . . because inside (green) lines don’t cross each other and outside (red) lines don’t cross each other.

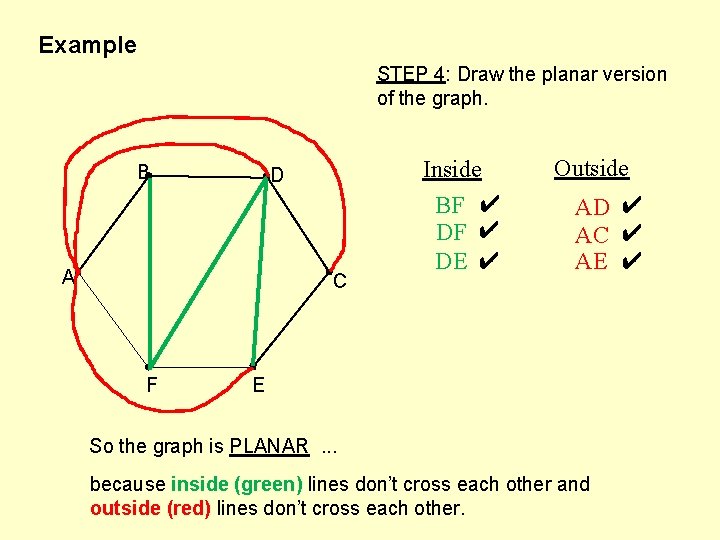
Example STEP 4: Draw the planar version of the graph. B D A C F Inside BF ✔ DE ✔ Outside AD ✔ AC ✔ AE ✔ E So the graph is PLANAR. . . because inside (green) lines don’t cross each other and outside (red) lines don’t cross each other.

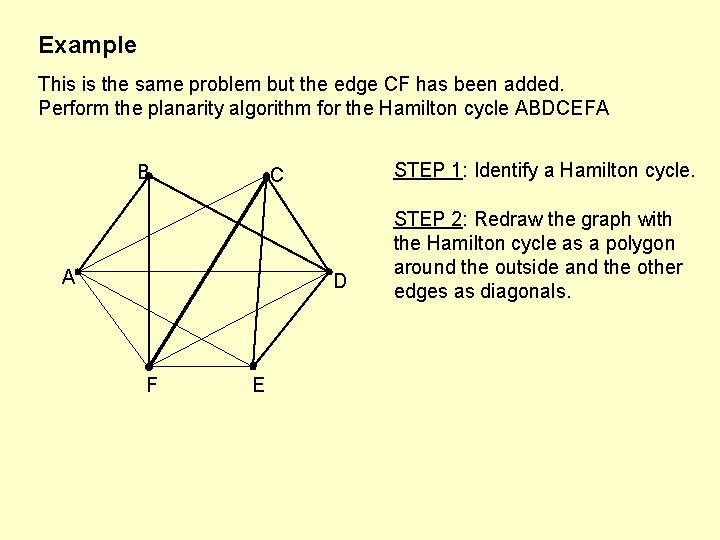
Example This is the same problem but the edge CF has been added. Perform the planarity algorithm for the Hamilton cycle ABDCEFA B STEP 1: Identify a Hamilton cycle. C A D F E STEP 2: Redraw the graph with the Hamilton cycle as a polygon around the outside and the other edges as diagonals.

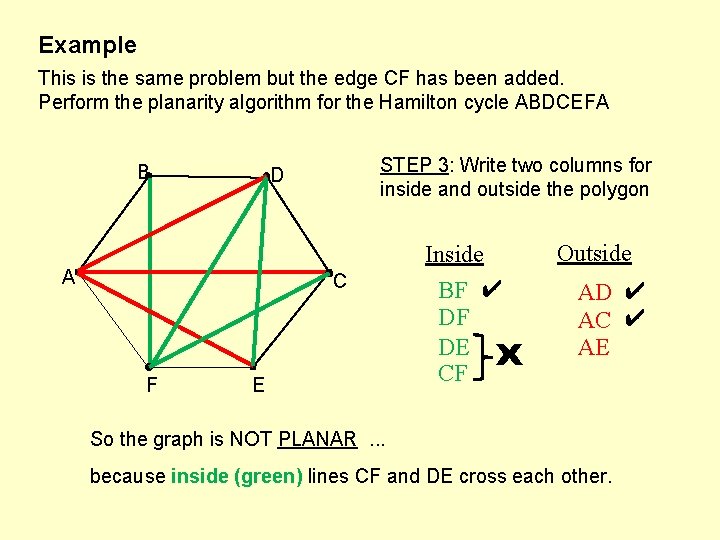
Example This is the same problem but the edge CF has been added. Perform the planarity algorithm for the Hamilton cycle ABDCEFA B STEP 3: Write two columns for inside and outside the polygon D A C F E Inside BF ✔ DF DE CF x Outside AD ✔ AC ✔ AE So the graph is NOT PLANAR. . . because inside (green) lines CF and DE cross each other.

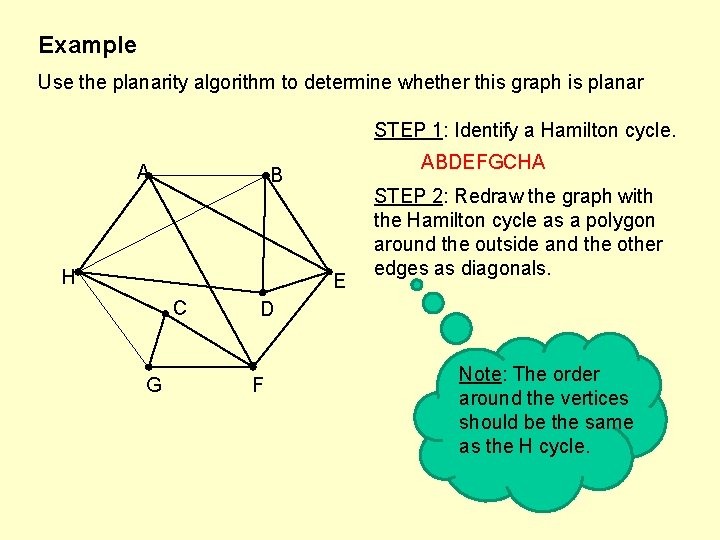
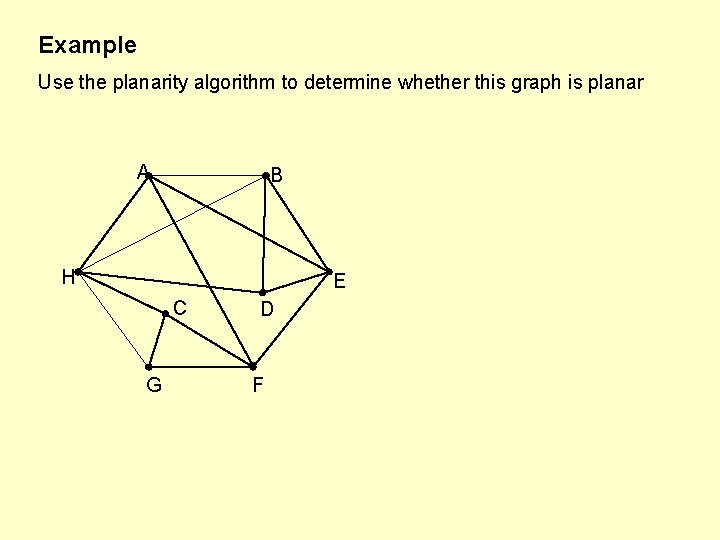
Example Use the planarity algorithm to determine whether this graph is planar STEP 1: Identify a Hamilton cycle. A ABDEFGCHA B H E C G STEP 2: Redraw the graph with the Hamilton cycle as a polygon around the outside and the other edges as diagonals. D F Note: The order around the vertices should be the same as the H cycle.

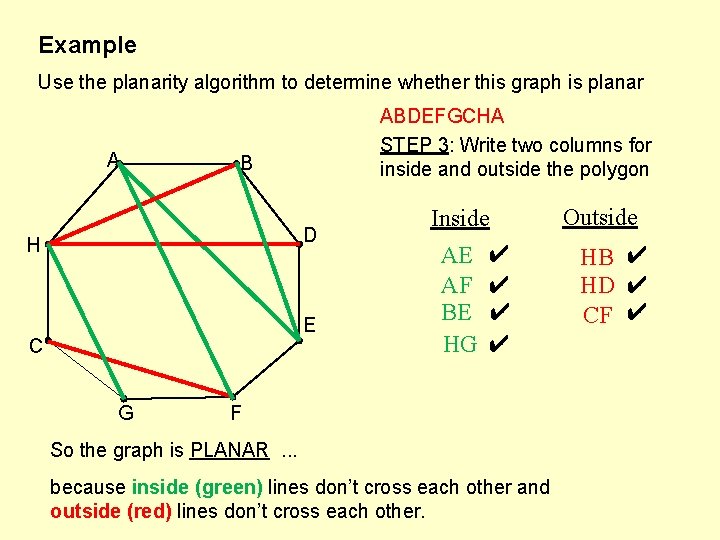
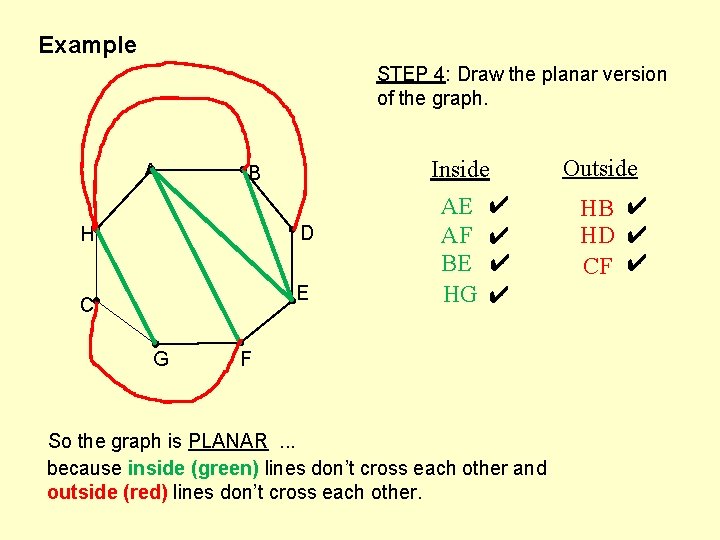
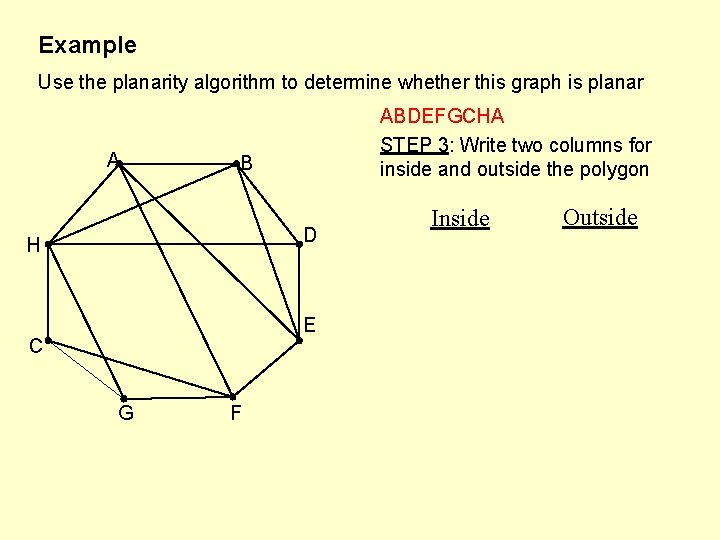
Example Use the planarity algorithm to determine whether this graph is planar A ABDEFGCHA STEP 3: Write two columns for inside and outside the polygon B D H E C G Inside AE AF BE HG ✔ ✔ F So the graph is PLANAR. . . because inside (green) lines don’t cross each other and outside (red) lines don’t cross each other. Outside HB ✔ HD ✔ CF ✔

Example STEP 4: Draw the planar version of the graph. A Inside B D H E C G AE AF BE HG ✔ ✔ F So the graph is PLANAR. . . because inside (green) lines don’t cross each other and outside (red) lines don’t cross each other. Outside HB ✔ HD ✔ CF ✔

Example Use the planarity algorithm to determine whether this graph is planar A B H E C G D F

Example Use the planarity algorithm to determine whether this graph is planar A ABDEFGCHA STEP 3: Write two columns for inside and outside the polygon B D H E C G F Inside Outside