Planarity and Higher Order Embeddings Shawn Cox CS

Planarity and Higher Order Embeddings Shawn Cox CS 594: Graph Theory 3 -5 -2014

Gas – Water – Electric Problem § Three Rivals all want service from the three utility services. § If any of the service lines cross, there will be a fight between the rivals § Is it possible for the utilities to lay the connections out so that no confrontations arise?

Gas – Water – Electric Problem § Turn the problem into a graph theory problem. – Rivals and Utilities are Vertices – Connections between them are Edges – Can we draw it without crossing?

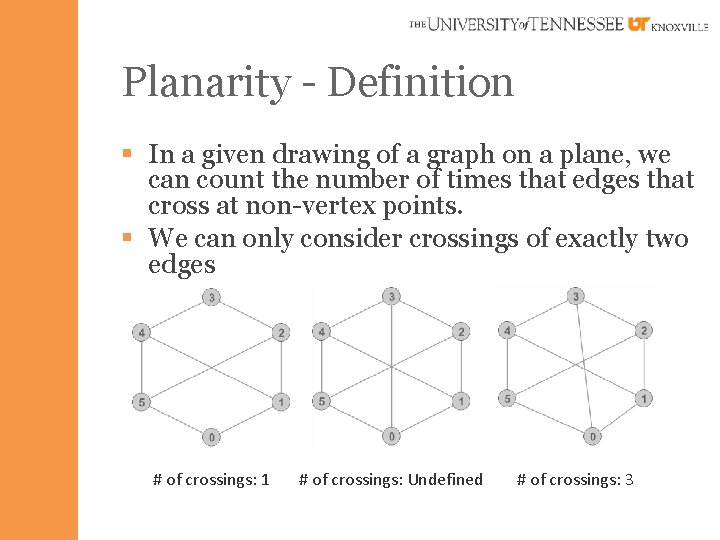
Planarity - Definition § In a given drawing of a graph on a plane, we can count the number of times that edges that cross at non-vertex points. § We can only consider crossings of exactly two edges # of crossings: 1 # of crossings: Undefined # of crossings: 3

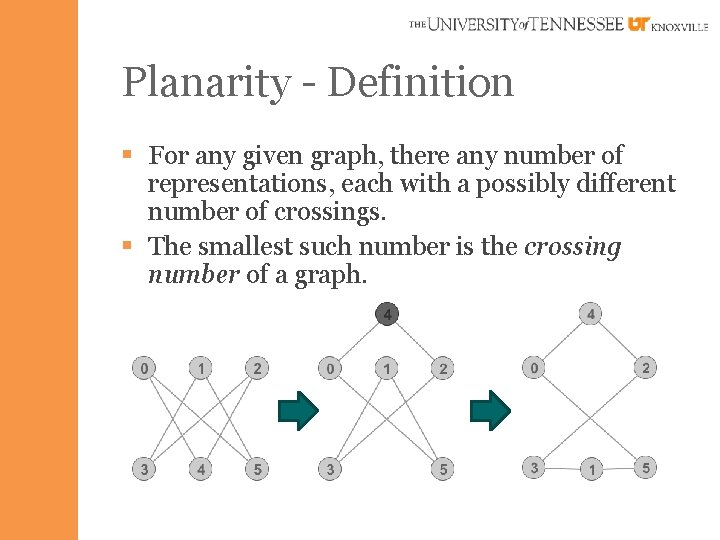
Planarity - Definition § For any given graph, there any number of representations, each with a possibly different number of crossings. § The smallest such number is the crossing number of a graph.

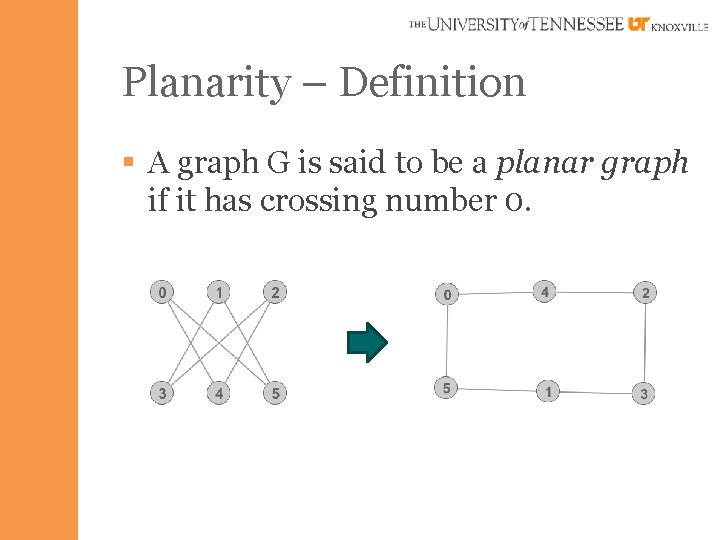
Planarity – Definition § A graph G is said to be a planar graph if it has crossing number 0.

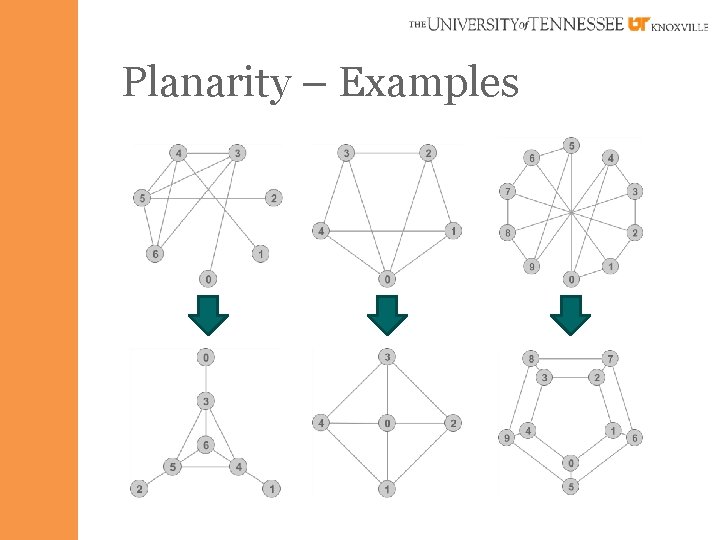
Planarity – Examples

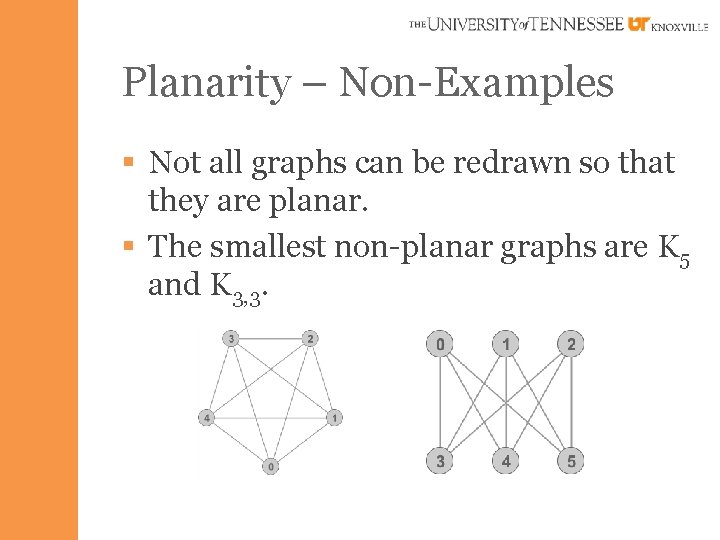
Planarity – Non-Examples § Not all graphs can be redrawn so that they are planar. § The smallest non-planar graphs are K 5 and K 3, 3.

Euler’s Characteristic for Planar Graphs § V–E+F=2 – V = # of vertices in the graph – E = # of edges in the graph – F = # of faces in the graph § Used to describe the shape of a graph

Euler’s Characteristic § Only holds for planar graphs § Unable to determine faces if intersecting edges are allowed

Disproving Planarity – K 5 § K 5 has 5 vertices and 10 edges. § If K 5 was planar, it would have 7 faces. § A planar graph with n vertices has at most 2/3 as many faces as it does edges – Why? Every edge is on exactly two faces, and every face has at least 3 edges on its boundary. § Seven faces is one face too many.

Disproving Planarity – K 3, 3 § K 3, 3 has 6 vertices and 9 edges. § If K 3, 3 was planar, it would have 5 faces. § A planar graph with n vertices that has no triangles has at most ½ as many faces as it does edges. – Similar to before, every edge is used twice, and every face has at least 4 edges on its boundary. § Once again, five faces is one too many.

Generalizing Arguments § Finding a disproof for every graph? § Instead, consider subgraphs of the original. § If there is exists a subgraph of G that is non-planar, then G is non-planar. – Alternatively, G is planar if all of its subgraphs are planar.

Formalized Arguments § Kuratowski’s Theorem – 1930 – Occasionally attributed to Lev Pontryagin as well, a Soviet Mathematician that claimed to have proven theorem, but never published a proof. § Wagner’s Theorem – 1937

Kuratowski’s Theorem § G is planar if and only if there is no subgraph of G that is a subdivision of K 5 or K 3, 3. § Any such subgraph is called a Kuratowski Subgraph

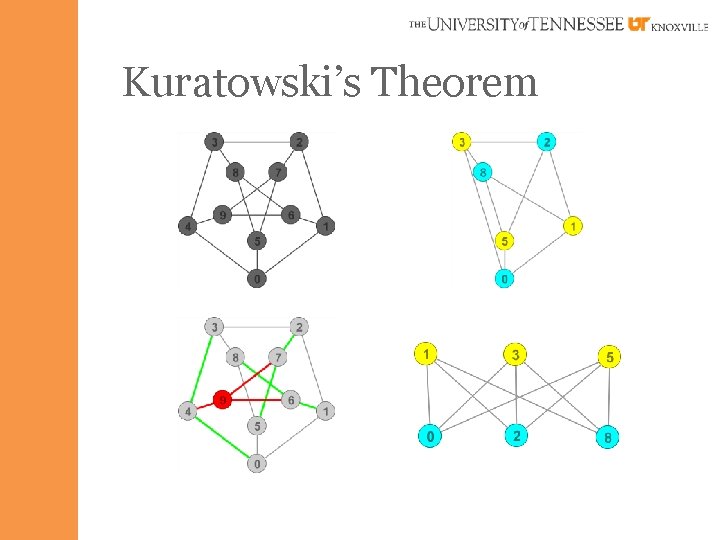
Kuratowski’s Theorem

Wagner’s Theorem – 1937 § G is planar if and only if there is no subgraph of G that is a minor of K 5 or K 3, 3. § Published seven years following Kurtowski’s theorem § Equivalent to Kuratowski’s proof, since it is easy to convert the appropriate minor into a subdivision and vice versa.

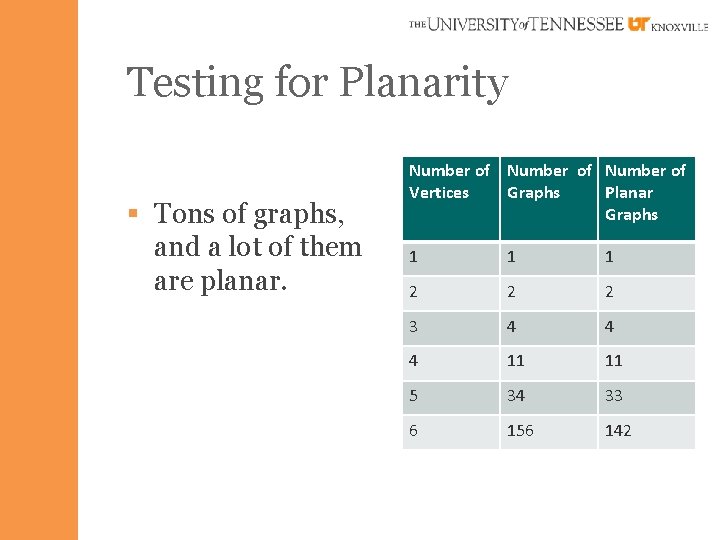
Testing for Planarity § Tons of graphs, and a lot of them are planar. Number of Vertices Graphs Planar Graphs 1 1 1 2 2 2 3 4 4 4 11 11 5 34 33 6 156 142

Testing for Planarity § Path Addition Method – Originally published by Hopcroft and Tarjan in 1974 for an O(n) algorithm § Vertex Addition Method – Published by Lempel, Even, and Cederbaum in 1967 for a O(n 2) algorithm – Improved by Even and Tarjan and then Booth and Leuker to O(n) – Outperforms Path Addition.

Results of Planarity § Draw it without crossing lines § Draw the graph with only straight lines (Fary’s Theorem) § Chromatic number of at least 4

Higher Order Analogies § Is the sphere different from the plane? – No. In fact the ability to draw a graph on one immediately gives you a drawing on the other. § What is different then? – The Torus provides a different space. • Certain graphs can be drawn with crossing number 0 on a toroid, but not on a plane. • Any such graph on the toroid has at most chromatic number 7 (Heawood Conjecture).

Genus 1 Embeddings § We can extend the notion of planarity to higher orders. – If we put a graph G on a toroid, we say that it is embedded on the toroid if it has crossing number 0. § We can color any genus 1 embedding with at most 7 colors. – The following is the canonical example of a 7 colorable toroidal embedding.

Open Problems § Any planar graph can be drawn with straight lines only, but can it be done with straight lines of integer lengths? (Harborth) – Can do done for cubic graphs, but not known for the general case.

Homework Problem 1 § Prove that the Heawood Graph (given below) is non-planar.

Homework 2 § Prove or Disprove: The following graph is planar.

Homework 3 § Prove or Disprove: The following graph is planar.

References § Kuratowski, Kazimierz (1930), "Sur le problème des courbes gauches en topologie", Fund. Math. (in French) 15: 271– 283. § Wagner, K. (1937), "Über eine Eigenschaft der ebenen Komplexe", Math. Ann. 114: 570– 590, doi: 10. 1007/BF 01594196. § Hopcroft, John; Tarjan, Robert E. (1974), "Efficient planarity testing", Journal of the Association for Computing Machinery 21 (4): 549– 568, doi: 10. 1145/321850. 321852. § Lempel, A. ; Even, S. ; Cederbaum, I. (1967), "An algorithm for planarity testing of graphs", in Rosenstiehl, P. , Theory of Graphs, New York: Gordon and Breach, pp. 215– 232.

References § Even, Shimon; Tarjan, Robert E. (1976), "Computing an stnumbering", Theoretical Computer Science 2 (3): 339– 344, doi: 10. 1016/0304 -3975(76)90086 -4. § Boyer & Myrvold (2004), p. 243: “Its implementation in LEDA is slower than LEDA implementations of many other O(n)time planarity algorithms. ” § Fáry, István (1948), "On straight-line representation of planar graphs", Acta Sci. Math. (Szeged) 11: 229– 233, MR 0026311. § Weisstein, Eric W. "Heawood Conjecture. " From Math. World-A Wolfram Web Resource. http: //mathworld. wolfram. com/Heawood. Conjecture. html