Planare Graphen Zeichnen von Graphen Proseminar Algorithmen auf

Planare Graphen Zeichnen von Graphen Proseminar Algorithmen auf Graphen Sommersemester 2006 Christoph Bösel

Überblick Begriff Euler-Satz Kuratowski-Satz Boyer-Myrvold-Algorithmus Demoucron-Algorithmus O(n) O(n²) Zeichnen Zusammenfassung, Fragen

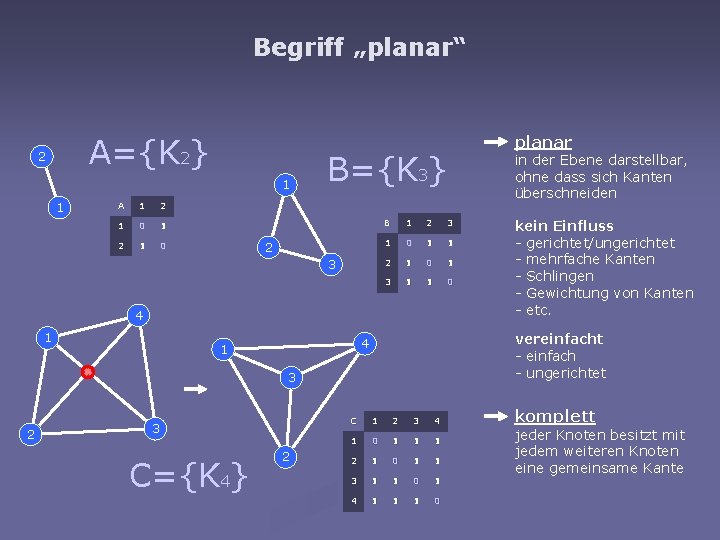
Begriff „planar“ A={K 2} 2 1 1 A 1 2 1 0 B={K 3} 2 3 B 1 2 3 1 0 1 1 2 1 0 1 3 1 1 0 4 1 3 2 3 C={K 4} 2 in der Ebene darstellbar, ohne dass sich Kanten überschneiden kein Einfluss - gerichtet/ungerichtet - mehrfache Kanten - Schlingen - Gewichtung von Kanten - etc. vereinfacht - einfach - ungerichtet 4 1 planar C 1 2 3 4 1 0 1 1 1 2 1 0 1 1 3 1 1 0 1 4 1 1 1 0 komplett jeder Knoten besitzt mit jedem weiteren Knoten eine gemeinsame Kante

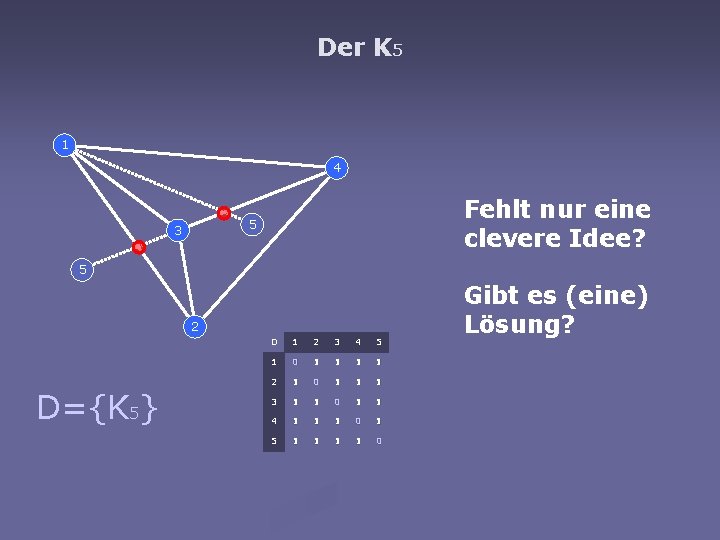
Der K 5 1 4 Fehlt nur eine clevere Idee? 5 3 5 2 D={K 5} D 1 2 3 4 5 1 0 1 1 2 1 0 1 1 1 3 1 1 0 1 1 4 1 1 1 0 1 5 1 1 0 Gibt es (eine) Lösung?

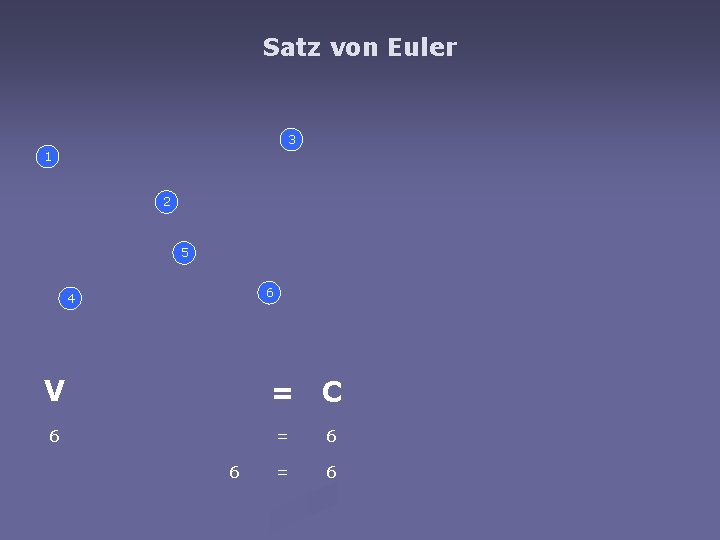
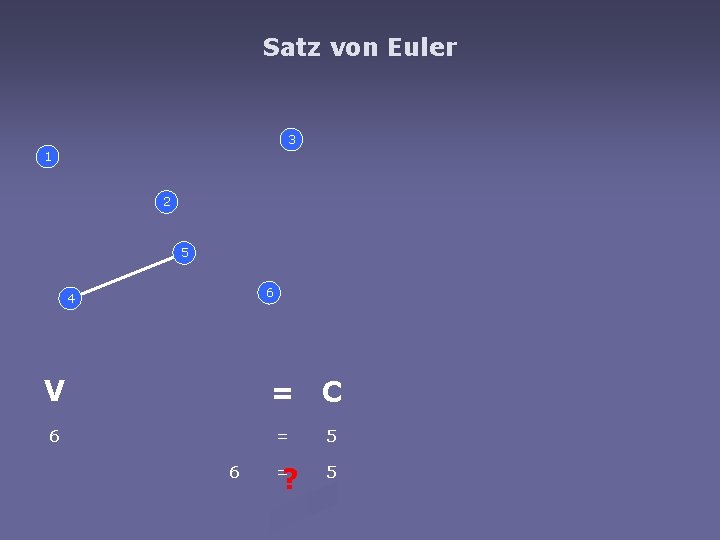
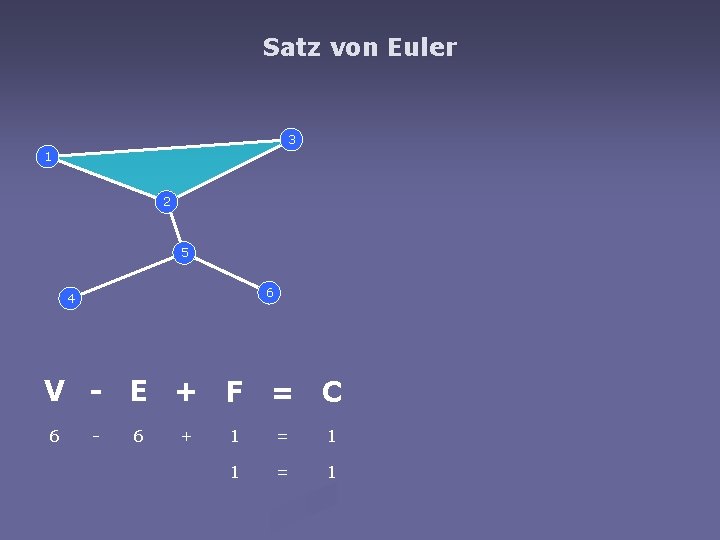
Satz von Euler 3 1 2 5 6 4 V = C 6 6 = 6

Satz von Euler 3 1 2 5 6 4 V = C 6 = 6 ? = 5 5

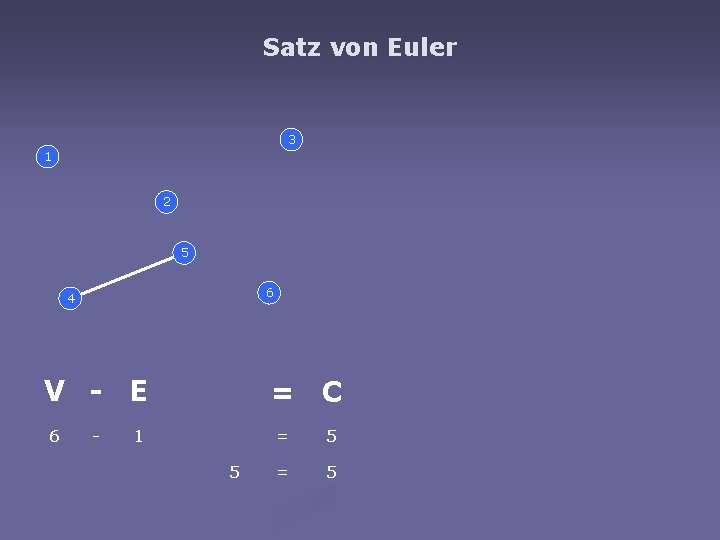
Satz von Euler 3 1 2 5 6 4 V - E 6 - = C 1 5 = 5

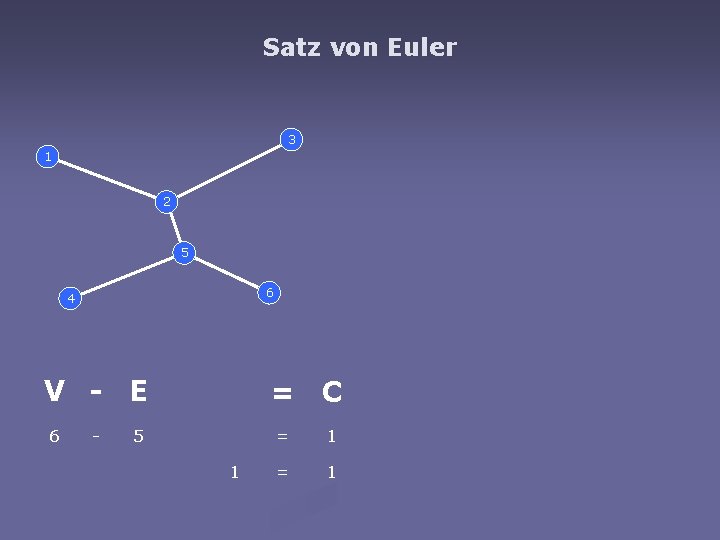
Satz von Euler 3 1 2 5 6 4 V - E 6 - = C 5 1 = 1

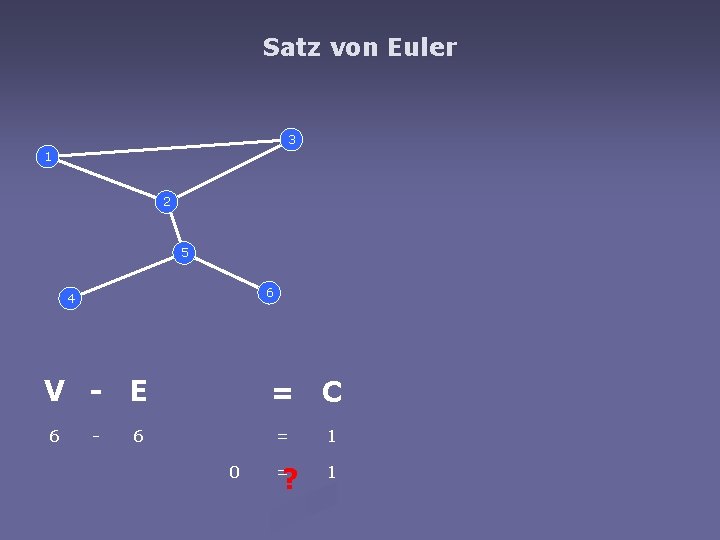
Satz von Euler 3 1 2 5 6 4 V - E 6 - = C 6 = 0 ? = 1 1

Satz von Euler 3 1 2 5 6 4 V - E + F = C 6 - 6 + 1 = 1

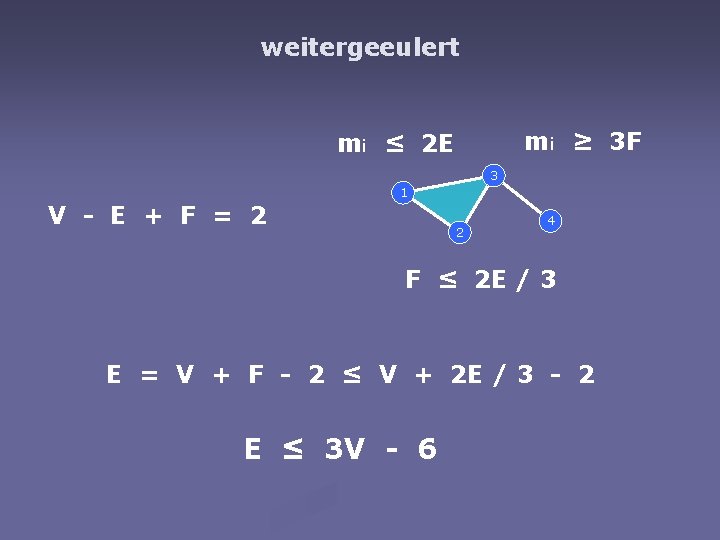
Satz von Euler 3 1 +E 2 [+V] v [+F] v [-C] 5 vereinfacht - zusammenhängend, C=1 6 4 V - E + F = C + 1 6 - 6 + 2 = 1 2 = 2 + 1

weitergeeulert mi ≥ 3 F mi ≤ 2 E 3 1 V - E + F = 2 2 4 F ≤ 2 E / 3 E = V + F - 2 ≤ V + 2 E / 3 - 2 E ≤ 3 V - 6

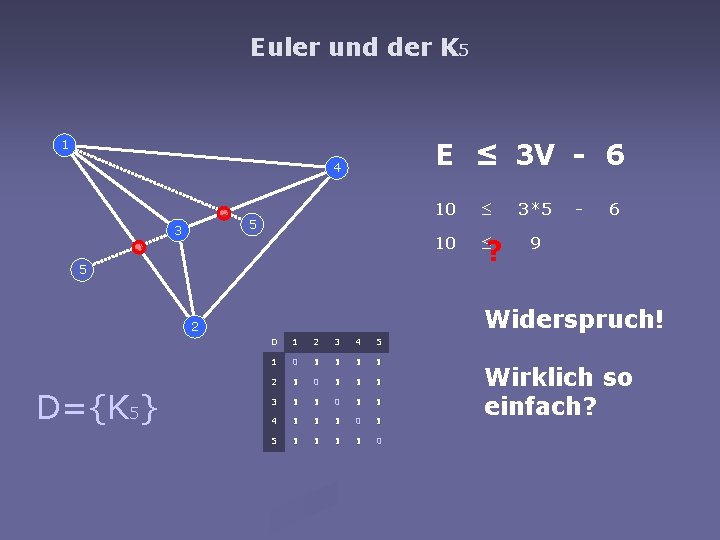
Euler und der K 5 E ≤ 3 V - 6 1 4 5 3 5 ≤ 10 ≤ ? 3*5 - 6 9 Widerspruch! 2 D={K 5} 10 D 1 2 3 4 5 1 0 1 1 2 1 0 1 1 1 3 1 1 0 1 1 4 1 1 1 0 1 5 1 1 0 Wirklich so einfach?

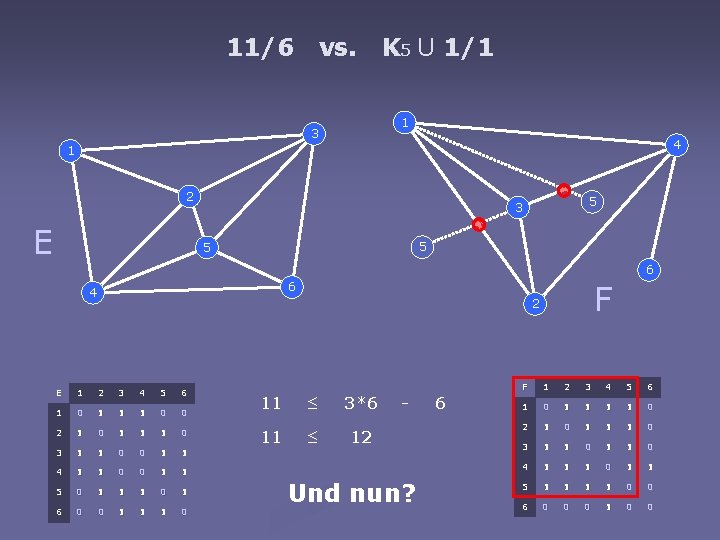
11/6 vs. K 5 U 1/1 1 3 4 1 2 E 5 3 5 5 6 F 6 4 2 E 1 2 3 4 5 6 1 0 1 1 1 0 0 2 1 0 1 1 1 0 3 1 1 0 0 1 1 4 1 1 0 0 1 1 5 0 1 1 1 0 1 6 0 0 1 1 1 0 11 ≤ 3*6 11 ≤ 12 - Und nun? 6 F 1 2 3 4 5 6 1 0 1 1 0 2 1 0 1 1 1 0 3 1 1 0 4 1 1 1 0 1 1 5 1 1 0 0 6 0 0 0 1 0 0

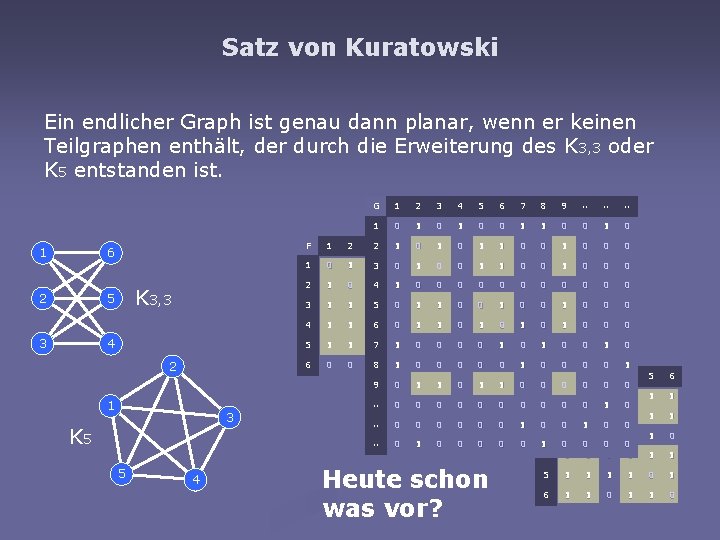
Satz von Kuratowski Ein endlicher Graph ist genau dann planar, wenn er keinen Teilgraphen enthält, der durch die Erweiterung des K 3, 3 oder K 5 entstanden ist. 1 6 2 5 3 K 3, 3 4 2 1 3 K 5 5 4 G 1 2 3 4 5 6 7 8 9 . . . 1 0 1 0 F 1 2 32 41 50 61 0 1 1 0 0 0 1 13 10 11 00 0 1 1 0 0 0 2 1 0 14 11 10 00 0 0 0 0 3 1 1 05 10 11 01 0 0 0 4 1 1 16 00 11 11 0 1 0 0 0 5 1 1 17 11 00 00 0 0 1 0 6 0 0 08 11 00 00 0 1 0 F 0 1 0 2 0 3 1 4 0 1 0 0 0 1 0 2 0 1 0 3 0 0 1 0 0 0 1 4 0 1 0 0 5 1 1 1 6 1 1 0 9 0 1 1 0 . . 0 0 0 1 . . 0 1 0 0 0 Heute schon was vor? 5 6 1 1 1 0

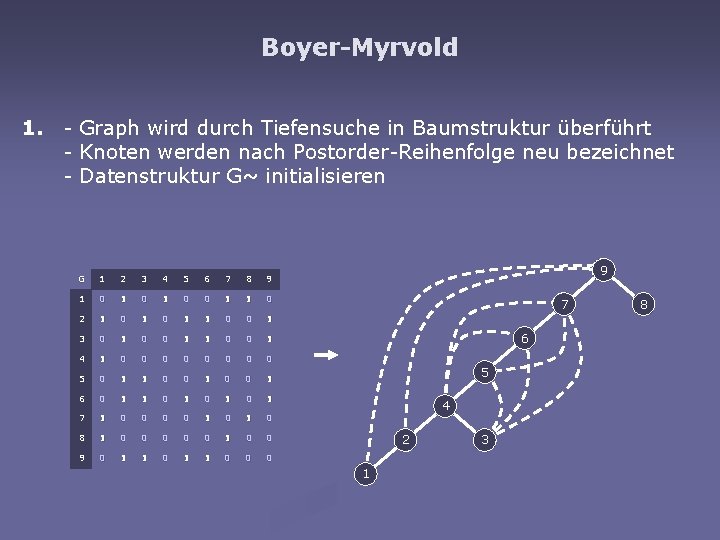
Boyer-Myrvold 1. - Graph wird durch Tiefensuche in Baumstruktur überführt - Knoten werden nach Postorder-Reihenfolge neu bezeichnet - Datenstruktur G~ initialisieren G 1 2 3 4 5 6 7 8 9 1 0 1 0 0 1 1 0 2 1 0 1 1 0 0 1 3 0 1 0 0 1 4 1 0 0 0 0 5 0 1 1 0 0 1 6 0 1 1 0 1 0 1 7 1 0 0 1 0 8 1 0 0 0 1 0 0 9 0 1 1 0 0 0 1 9 2 7 3 6 5 4 6 2 7 1 8 3 9 4 8

Boyer-Myrvold 2. for jeden Knoten v = 1 to n 3. for jedes Kind c von v in G Baumkante (vc, c) in G~ einfügen 4. for jede Rückkante, indizent zu v und einem Nachfolger w Walkup(G~, v, w) 5. for jedes Kind c von v in G Walkdown(G~, vc) 6. for jede Rückkante, indizent zu v und einem Nachfolger w if (vc, w) є/ G~ Kuratowski-Teilgraphen aus G~ isolieren return (nicht planar, G~) 7. return (planar, G~)

Boyer-Myrvold positiv: - Laufzeit O(n) - Rückgabe von - Entscheidung planar/nicht-planar - Kuratowski-Teilgraph (wenn nicht planar) - Einbettung (wenn planar) - robust - einfacher als andere O(n)-Algorithmen negativ: - immernoch recht komplex

Demoucron 1. beliebigen Kreis aus G in G‘ einbinden 2. alle Flächen von G‘ bestimmen 3. F(S) bestimmen (verbleibende Fragmente von G) 4. if F(S)=O / then 5. für alle F(S) die angrenzbaren Flächen bestimmen 6. if es gibt F(S) ohne solche Fläche then 7. if es gibt F(S) mit nur einer Fläche then 8. Fragment von F(S) aussuchen 9. α-Pfad aussuchen und in angrenzbare Fläche einbinden 10. goto 2. return planar return nicht-planar goto 9.

Demoucron positiv: - einfach zu implementieren negativ: - Laufzeit O(n²) - keine Rückgabe außer planar/nicht-planar

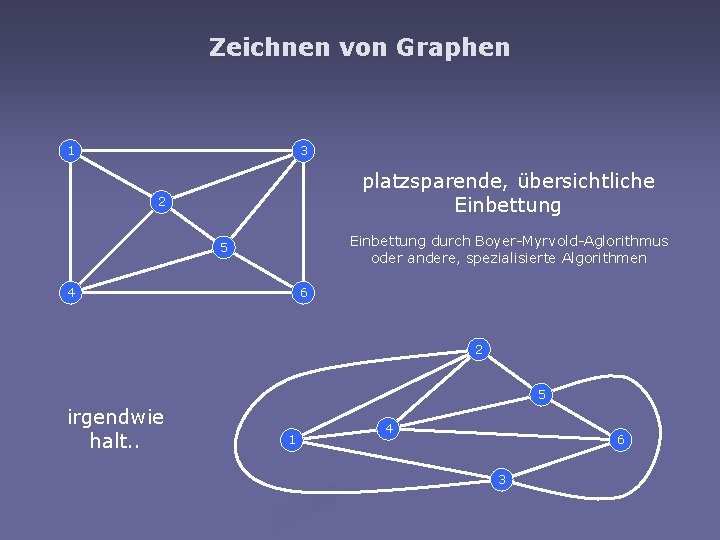
Zeichnen von Graphen 1 3 platzsparende, übersichtliche Einbettung 2 Einbettung durch Boyer-Myrvold-Aglorithmus oder andere, spezialisierte Algorithmen 5 4 6 2 5 irgendwie halt. . 1 4 6 3

Zusammenfassung planar – p wie platt K 5 und K 3, 3 - die Wurzeln alles Bösen Grundversorgung durch einfache, aber zeiltlich aufwändige Algorithmen mit quadratischer Laufzeit leistungsstarke Algorithmen mit linearer Laufzeit und jeder Menge Goodies, jedoch sehr komplex übersichtliche Zeichnung als Erweiterung des Planaritätstests

Fragen?