Planar straight line graph A planar straight line

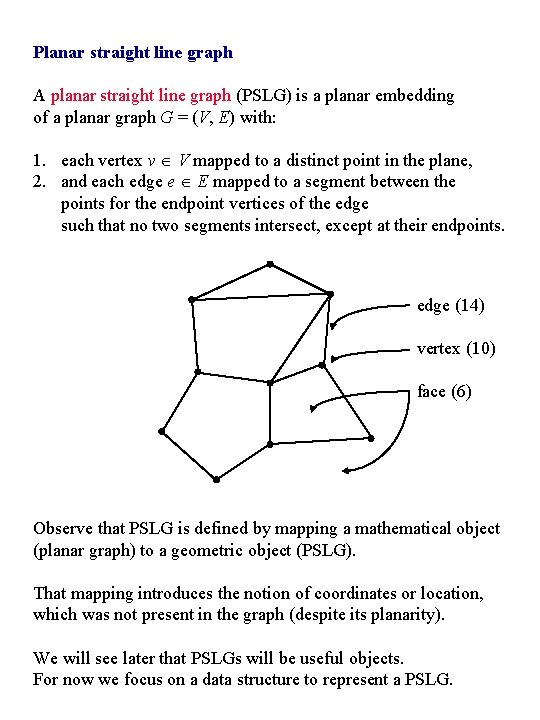
Planar straight line graph A planar straight line graph (PSLG) is a planar embedding of a planar graph G = (V, E) with: 1. each vertex v V mapped to a distinct point in the plane, 2. and each edge e E mapped to a segment between the points for the endpoint vertices of the edge such that no two segments intersect, except at their endpoints. edge (14) vertex (10) face (6) Observe that PSLG is defined by mapping a mathematical object (planar graph) to a geometric object (PSLG). That mapping introduces the notion of coordinates or location, which was not present in the graph (despite its planarity). We will see later that PSLGs will be useful objects. For now we focus on a data structure to represent a PSLG.

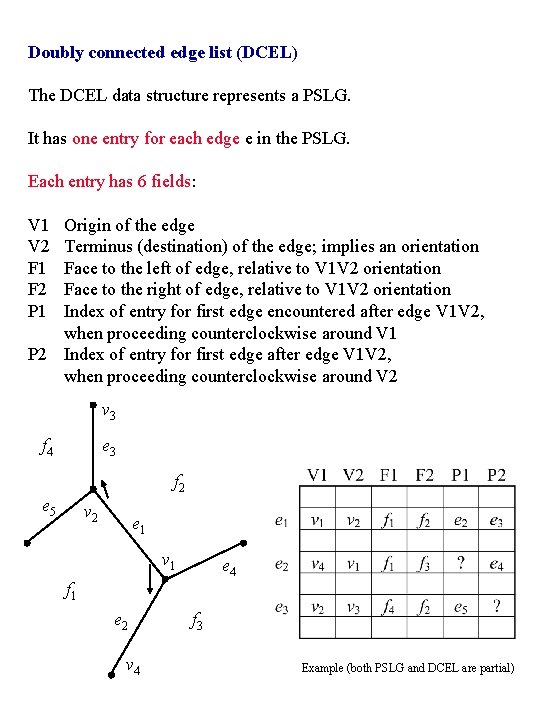
Doubly connected edge list (DCEL) The DCEL data structure represents a PSLG. It has one entry for each edge e in the PSLG. Each entry has 6 fields: V 1 V 2 F 1 F 2 P 1 Origin of the edge Terminus (destination) of the edge; implies an orientation Face to the left of edge, relative to V 1 V 2 orientation Face to the right of edge, relative to V 1 V 2 orientation Index of entry for first edge encountered after edge V 1 V 2, when proceeding counterclockwise around V 1 P 2 Index of entry for first edge after edge V 1 V 2, when proceeding counterclockwise around V 2 v 3 f 4 e 3 f 2 e 5 v 2 e 1 v 1 e 4 f 1 e 2 v 4 f 3 Example (both PSLG and DCEL are partial)

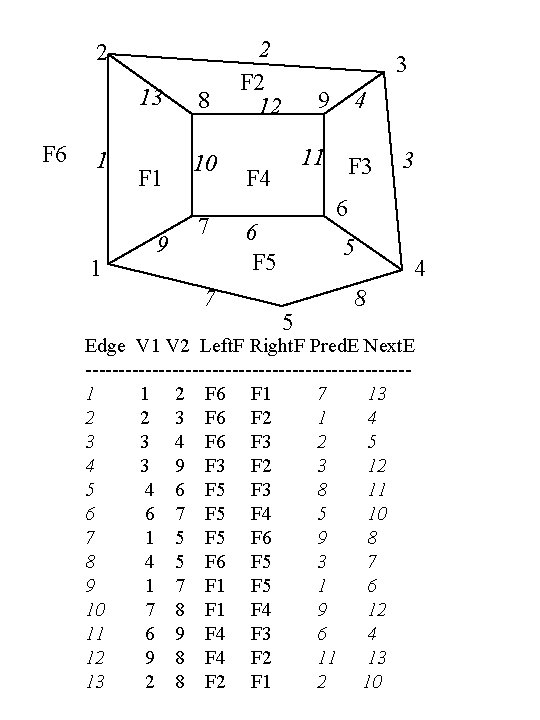
2 13 F 6 1 1 F 1 9 8 10 7 7 2 F 2 12 3 9 4 11 F 3 F 4 3 6 6 F 5 5 5 4 8 Edge V 1 V 2 Left. F Right. F Pred. E Next. E ------------------------1 1 2 F 6 F 1 7 13 2 2 3 F 6 F 2 1 4 3 3 4 F 6 F 3 2 5 4 3 9 F 3 F 2 3 12 5 4 6 F 5 F 3 8 11 6 6 7 F 5 F 4 5 10 7 1 5 F 6 9 8 8 4 5 F 6 F 5 3 7 9 1 7 F 1 F 5 1 6 10 7 8 F 1 F 4 9 12 11 6 9 F 4 F 3 6 4 12 9 8 F 4 F 2 11 13 13 2 8 F 2 F 1 2 10

Data structures If the PSLG has N vertices, M edges and F faces then we know N - M +F = 2 by Euler’s formula. DCEL can be described by six arrays: V 1[1: M], V 2[1: M], Left. F[1: M] Right[1: M], Pred. E[1: M] and Next. E[1: M]. Since both the number of faces and edges are bounded by a linear function of N, we need O(N) storage for all these arrays. Define array HV[1: N] with one entry for each vertex; entry HV[i] denotes the minimum numbered edge that is incident on vertex vi and is the first row or edge index in the DCEL where vi is in V 1 or V 2 column. Thus for our example in the preceding slide HV=(1, 1, 2, 3, 7, 5, 6, 10, 4]. Similarly, define array HF[1: F] where F= M-N+2 , with one entry for each face; HF[i] is the minimum numbered edge of all the edges that make the face HF[i] and is the first row or edge index in the DCEL where Fii is in Left. F or Right. F column. For our example, HF=(1, 2, 3, 6, 5, 1). Both HV and HF can be filled in O(N) time each by scanning DCEL.

DCEL operations Procedure Edges. Incident use a DCEL to report the edges incident to a vertex vj in a PSLG. The edges incident to vj are given as indexes to the DCEL entries for those edges in array A [1: 3 N-6] since M<= 3 N-6. 1 procedure Edges. Incident(j) 2 begin 3 a = HV[j] /* Get first DCEL entry for vj, a is index. */ 4 a 0 = a /* Save starting index. */ 5 A[1] = a 6 i=2 /* i is index for A */ 7 if (V 1[a] = j) then /* vertex j is the origin */ 8 a =Pred. E[a] /* Go on to next incident edge. */ 9 else /* vertex j is the destination vertex of edge a */ 10 a =Next. E[a] /* Go on to next incident edge. */ 11 endif 12 while (a a 0) do /* Back to starting edge? */ 13 A[i] = a 14 if (V 1[a] = j) then 15 a = Pred. E[a] /* Go on to next incident edge. */ 16 else 17 a = Next. E[a] /* Go on to next incident edge. */ 18 endif 19 i=i+1 V 2[a] Next. E[a] 20 endwhile 21 end a V 1[a] Pred. E[a]

If we make the following changes, it will become a procedure Faceincident[j] giving all the edges that constitute a face: 3: a = HF[j] And sustitute HV by HF and V 1 by F 1. A will have a size A[1: N]. Both Edges. Incident and Faceincident requires time proportional to the number of incident edges reported. How does that relate to N, the number of vertices in the PSLG? We have these facts about planar graphs (and thus PSLGs): (1) (2) (3) (4) v-e+f=2 e 3 v - 6 f 2/3 e f 2 v - 4 where Euler’s formula v = number of vertices = N e = number of edges=M f = number of faces=F v O(N) by definition e O(N) by (2) Edges. Incident requires time O(N) and DCEL requires storage O(N), one entry per edge.