Planar graphs with no 5 cycles 6 cycles

Planar graphs with no 5 cycles, 6 -cycles or intersecting triangles are 3 -colorable Carl Yerger, Davidson College Clemson Mini-Conference 2012

A Historical Problem n n n Grotzsch’s Theorem (1959): Any planar graph that contains no 3 -cycles is 3 -colorable. Thomassen found several short proofs of Grotzsch’s theorem as a consequence of some of his other results. Are there other classes of graphs that exclude certain length cycles that are 3 -colorable?

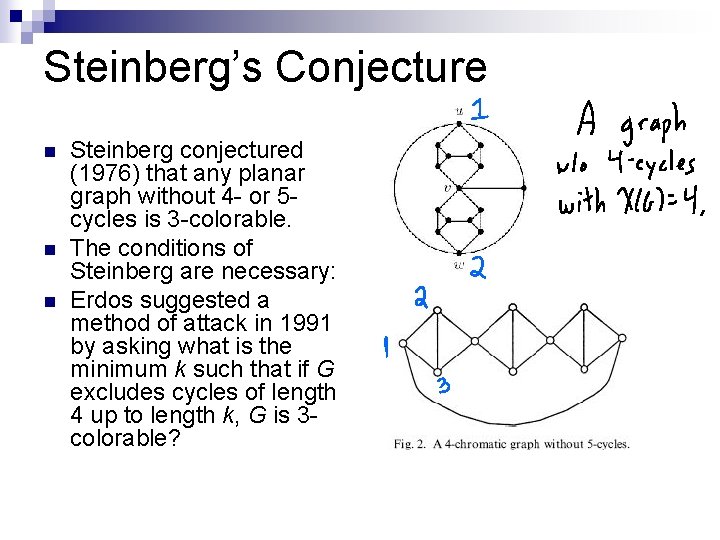
Steinberg’s Conjecture n n n Steinberg conjectured (1976) that any planar graph without 4 - or 5 cycles is 3 -colorable. The conditions of Steinberg are necessary: Erdos suggested a method of attack in 1991 by asking what is the minimum k such that if G excludes cycles of length 4 up to length k, G is 3 colorable?

Progress on Steinberg - Coloring n n n Results for k = 11, 9, 8, 7. The most recent result within the paradigm of Erdos is that of Borodin et al (2005) who show that k ≤ 7. Proof Technique for k = 7: Show that every proper 3 -coloring of the vertices of any single face of length 8 to 11 in a connected graph G that excludes cycles of length 4 through 7 extends to a proper 3 -coloring of G. The proof of this theorem uses discharging.

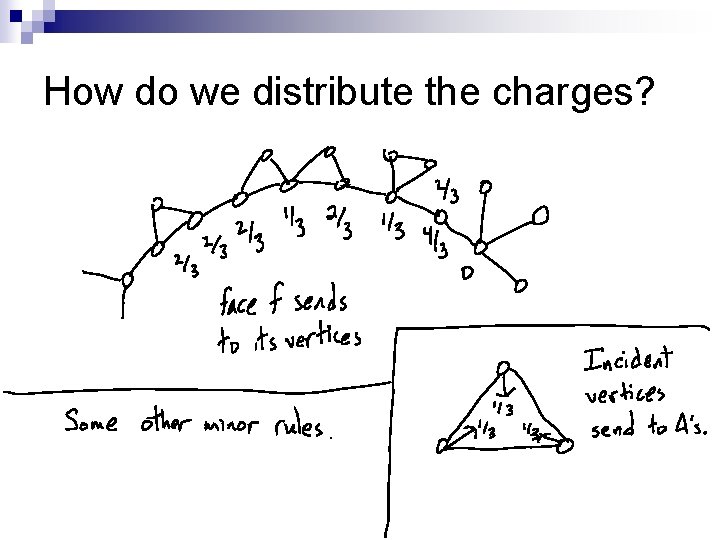
Discharging n Euler’s Formula: Give all vertices charge n Give all faces charge except a precolored face, which is given n Goal: We want all vertices and faces to have nonnegative charge (positive charge for precolored face). n

How do we distribute the charges?

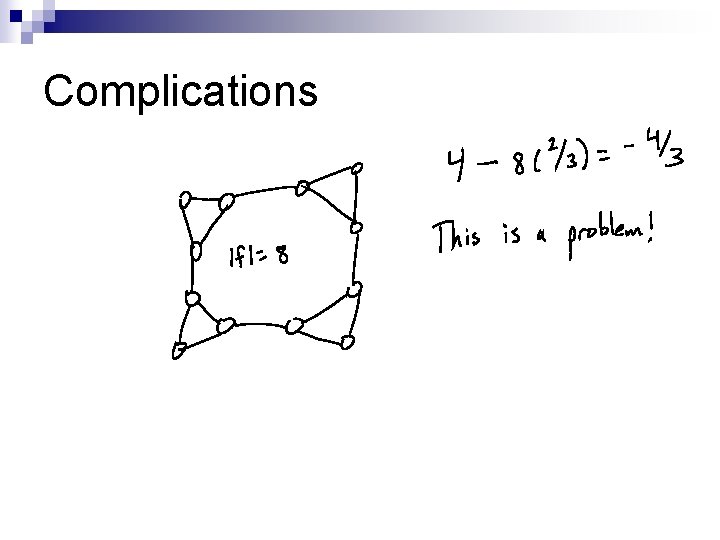
Complications

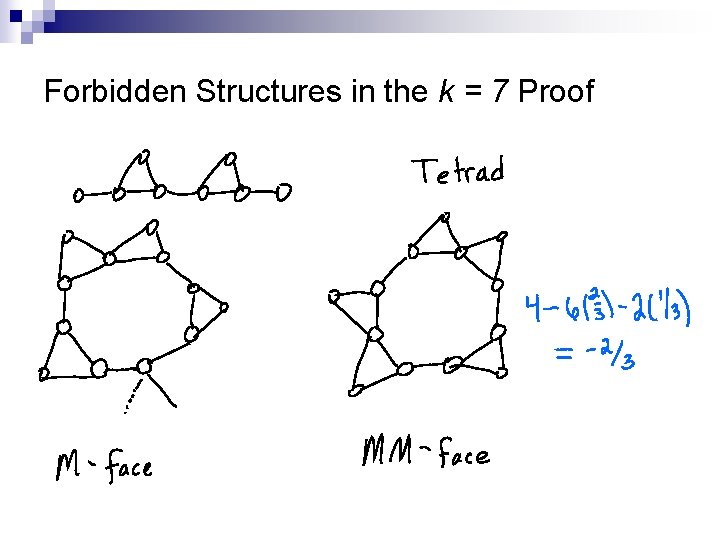
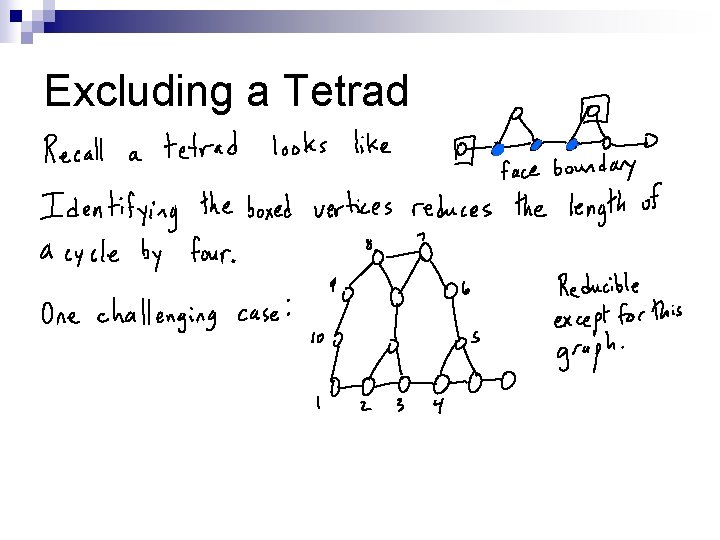
One Forbidden Structure: A Tetrad n n n If G were a minimum counterexample and contained a tetrad, identify vertices x and t. Delete vertices. If the resulting graph is 3 colorable, then the original graph is 3 -colorable. Excluding tetrads gives faces more charge after discharging, which allows us to prove that such a minimal counterexample does not exist.

The k = 7 proof n n n Consider a minimal counterexample. Begin with a graph G having a 3 -colored face, D. The aim is to prove structural properties. No separating cycles of length at most 11. G is 2 -connected, vertices of degree 2 must be part of D. No cycle of length at most 13 has a nontriangular chord, nor does D.

Forbidden Structures in the k = 7 Proof

Steinberg’s Conjecture and Higher Surfaces n n The condition given by Erdos holds for arbitrary surfaces: Zhao showed that for every surface Σ, there exists some k such that if G is a graph embedded on Σ, and G has no cycles of length 4 through k, then G is 3 -colorable. Unfortunately, for surfaces with nonpositive Euler characteristic the bound for k is given by. Euler characteristic of some simple surfaces are plane = 2, torus = 0, Klein bottle = 0, double torus = -2, etc. Example: Double torus, k = 35.

A Topological Result We prove that k = 10 with a linear size of minimal exceptions. n Theorem [Thomas, CY]: Let Σ be a surface of Euler genus g. If G is 4 -critical and has no cycles of length four through ten, then n

A similar construction n [Dvorak, Thomas] If G is a 4 -critical, triangle free graph drawn on a torus, then

Tightness of this bound On the plane, when cycles of length 4 through 9 are excluded, no 4 -critical graphs exist by the result of Borodin et al. n On higher surfaces 4 -critical graphs do exist since there are graphs with arbitrarily large girth and chromatic number. n The Hajos construction allows us to construct a sequence of critical graphs with size linear in the genus of G. n

Intersecting Triangles n n n By including triangles spaced far apart, we can reduce the cycle restrictions dramatically. 2010: Borodin and Glebov showed that every planar graph excluding 5 -cycles and with minimum distance between triangles at least two is 3 colorable. The (Strong) Bordeaux Coloring Conjecture: (Borodin and Raspaud) Can we reduce the restriction to only (adjacent) intersecting triangles and 5 cycles?

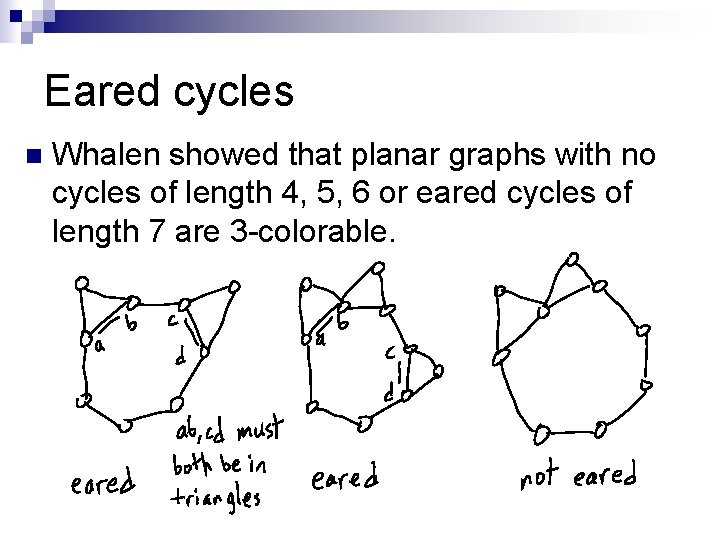
Eared cycles n Whalen showed that planar graphs with no cycles of length 4, 5, 6 or eared cycles of length 7 are 3 -colorable.

Methodology n n Whalen seeks a minimum counterexample and proves the customary pre-colored cycle analogue: Theorem: Let G be a plane graph with outer cycle of length at most 11. Suppose G excludes cycles of length 4, 5, 6 and eared cycles of length 7. Suppose G does not contain a vertex adjacent to three vertices on the outer cycle. Then any proper 3 -coloring of the outer cycle extends to a proper 3 -coloring of G.

Coloring with an Independent Set and a Forest n Can we partition the vertices of a graph into an independent set and a set that induces a forest?

How does this relate to Steinberg? Coloring with an independent set and a forest is stronger than 3 -coloring. n Does there exist a planar graph excluding 4 -cycles and 5 -cycles that is not colorable with an independent set and a forest? n Suggests a possible extension of Steinberg’s conjecuture. n

Borodin’s Technique n n n A common technique for solving problems related to Steinberg’s conjecture is to examine what happens inside a precolored cycle. Colorings inside and outside the cycle do not affect each other. What about for an independent set and a forest?

An extension of Grotzsch’s Theorem n n Kawarabayashi and Thomassen (2008) proved the following: Let G be a plane graph. Assume that every triangle of G has a vertex v which is on the outer face boundary and such that v is contained in no 4 -cycle. Assume also that the distance between any two triangles is at least 5. Then G has chromatic number at most 3. This is proved with the help of a structural theorem in coloring with an independent set and a forest.

Our Theorem: Let G be a planar graph that excludes 5 -cycles, 6 -cycles and intersecting triangles. Then G is 3 colorable. n Proof uses a discharging technique and strategies similar to the proof of Borodin and Glebov. n

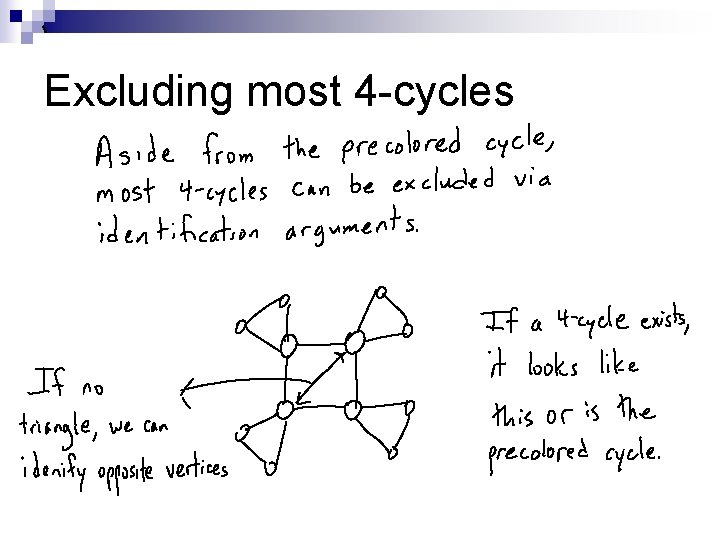
General Strategy n n Assume that there exists a pre-colored cycle of length 7 through 10 and other basic structural properties hold. Describe a set of discharging rules. Exclude various structures, including tetrads, most 4 -cycles and some 7 -cycles and 8 -cycles. Show that every vertex and face has nonnegative charge, contradicting Euler’s formula.

The Discharging Rules, I

The Discharging Rules II

Excluding a Tetrad

Excluding most 4 -cycles

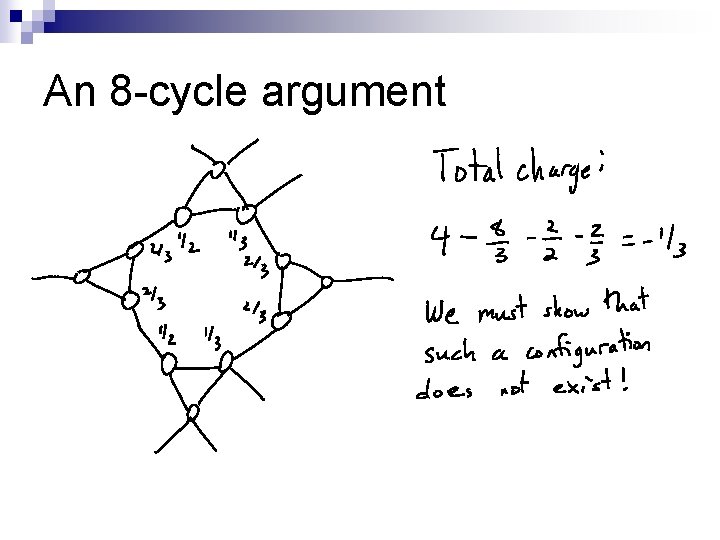
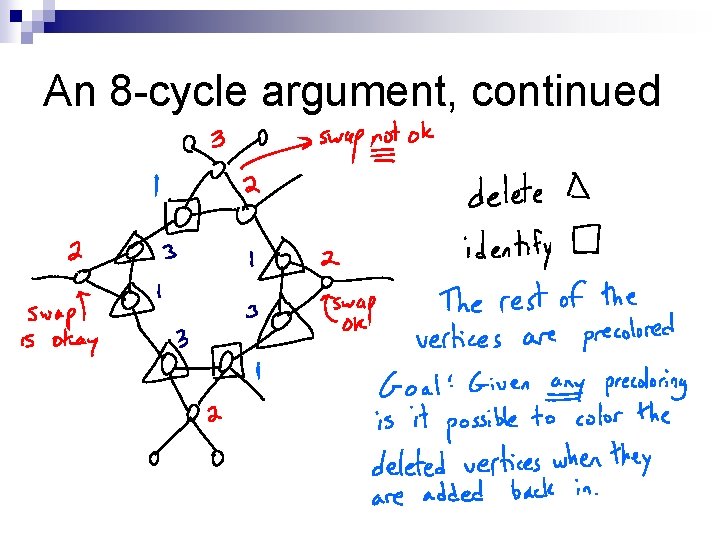
An 8 -cycle argument

An 8 -cycle argument, continued

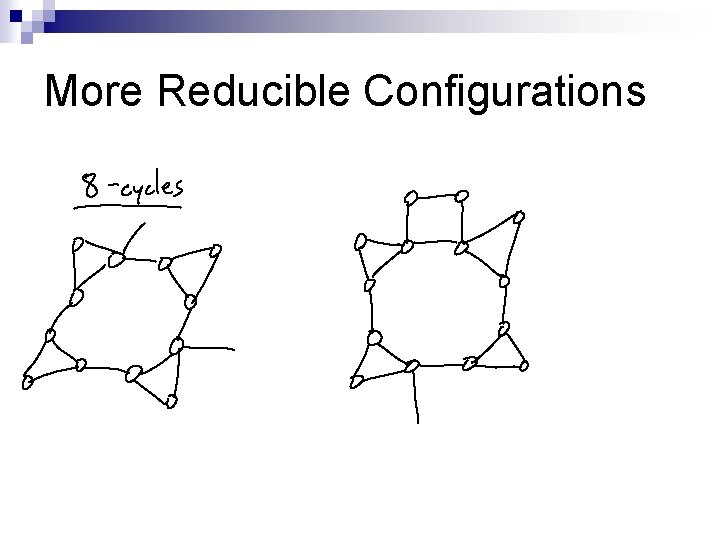
Reducible Configurations

More Reducible Configurations

Wrap-up To finish the proof, we must show each of the previous configurations is reducible. n All remaining face combinations must have charge at least zero via the discharging rules alone. n We get a contradiction via Euler’s formula. n

Future directions n n Cycles of length seven are the more challenging case for Steinberg. No known counterexample for the Steinberg conditions for an independent set and a set that induces a forest. Need another idea to push discharging to work for Steinberg’s conjecture. Other types of coloring?

Thank you for your attention! Any questions?