PKDGRAV A Parallel kD Tree Gravity Solver for

PKDGRAV: A Parallel k-D Tree Gravity Solver for N-Body Problems Derek C. Richardson (U Maryland) FMM 2004

Overview l High-performance cosmology code. l Written at U Washington N-body shop by Joachim Stadel (U Zurich) & Tom Quinn. l Now adapted for a variety of applications, including planet formation. l Lastest version has implementation of SPH (smoothed particle hydrodynamics).

Sample Movie

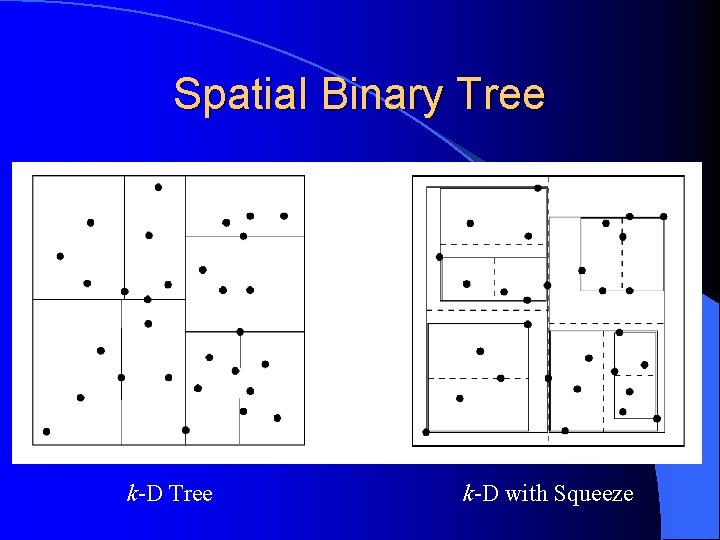
Spatial Binary Tree l Ironically, PKDGRAV no longer uses a k-D tree for gravity… l The problem: elongated cells can give large multipole moments and other pathologies. l The solution: spatially bisect cells and squeeze the cell boundaries. l Also good for neighbour searching.

Spatial Binary Tree k-D with Squeeze

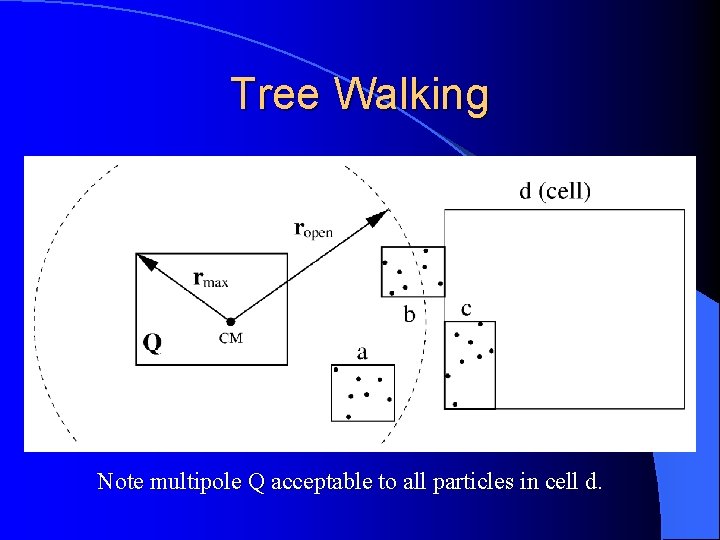
Tree Walking l Construct particle-particle and particle-cell interaction lists from top down. l Define opening ball (based on ) to test for ball-bucket intersection. – If bucket outside ball, apply multipole (c-list). – Otherwise open cell and test its children, etc. , until leaves reached (which go on p-list). l Nearby cells have similar lists: amortize.

Tree Walking Note multipole Q acceptable to all particles in cell d.

Other Issues l Multipole expansion order. – Use hexadecapole (best bang for buck). l Force softening. – Use spline-softened gravity kernel. l Periodic boundary conditions. – Use Ewald summation technique. l Time steps. – Use hierarchical steps (adaptive leapfrog).

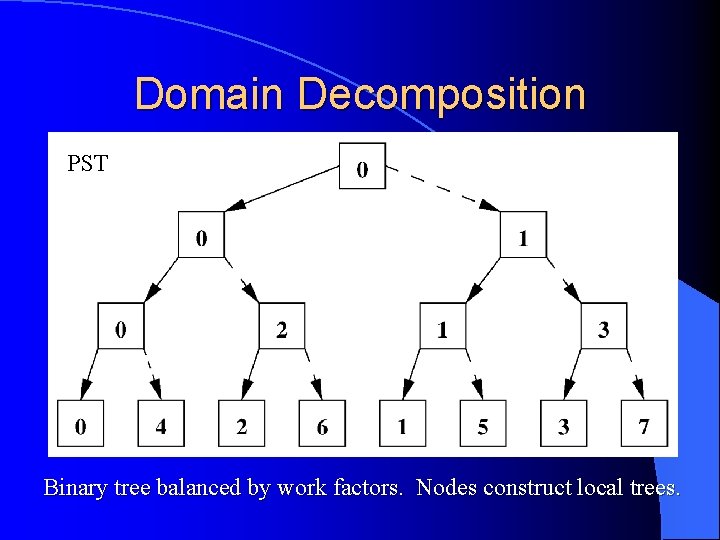
Parallel Implementation 1. Master layer (serial). 1. 2. Processor Set Tree (PST) layer (parallel). 1. 3. Assigns tasks to processors. Parallel k-D (PKD) layer (serial). 1. 4. Controls overall flow of program. MIMD execution of tasks. Machine-dependent Layer (MDL, separate). 1. Interface to parallel primitives.

Domain Decomposition PST Binary tree balanced by work factors. Nodes construct local trees.

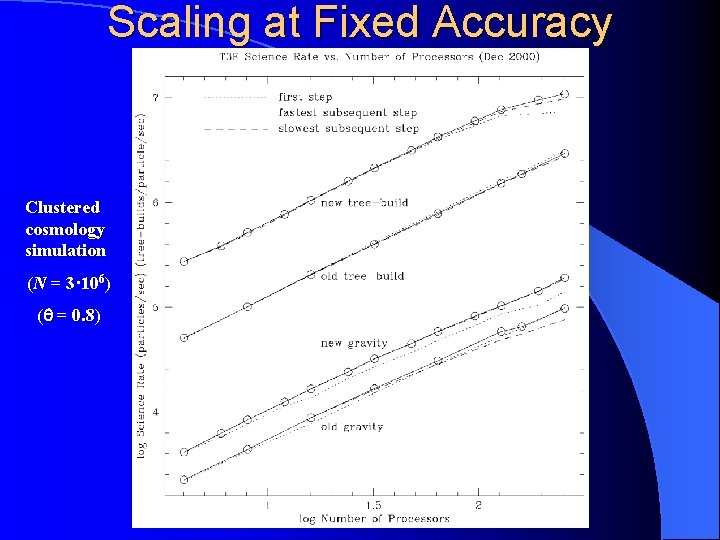
Scaling at Fixed Accuracy Clustered cosmology simulation (N = 3· 106) ( = 0. 8)

Some Science: Planetesimals l One of the recent additions to PKDGRAV is the ability to treat particle collisions. l Applications: – – – Planet formation (planetesimal growth). Asteroid disruption. Planetary rings. l Technique: predict collision during leapfrog drift step using fast neighbour search.

Planetesimal Evolutionary models based on laboratory experiments may be inadequate. – Outcomes determined by gravitational reaccumulation. Leinhardt et al. 2000

Incorporating Collision Models l Based on individual test cases, collision outcomes can be incorporated into large-scale sims of planet formation.

Near-Earth Asteroid Binaries l Reaccumulation following tidal disruption could form NEA binaries. l Need reaccumulated (or shattered/fragile) body to start with…

New Code: Rigid Aggregates l Recently the ability to treat collections of particles as rigid aggregates has been added. l Applications include realistic asteroid shape models and more complex granular shapes. l Technique: solve Euler rigid body equations of motion with torque and allow for noncentral impacts.

Rigid Aggs: Movie 1

Rigid Aggs: Movie 2 Bouncing Allowed No Bouncing

Rigid Aggs: Movie 3

Rigid Aggs: Movie 4

Future Work l PKDGRAV continues to be improved. l Algorithms currently being considered: – Local expansions. – Tree repair. – Improved collision detection. l Other possibilities include combining PKDGRAV with a Grape board!…