PKCS 1 v 2 1 RSA Cryptography Standard

PKCS #1 v 2. 1: RSA Cryptography Standard Burt Kaliski, RSA Laboratories PKCS Workshop, 5 October 2000

History of PKCS #1 • June 1991: PKCS #1 v 1. 4 – initial RSA encryption, signature schemes • Nov. 1993: PKCS #1 v 1. 5 – minor editorial revisions – wide deployment, in parallel with increased understanding of security of RSA-based techniques • July 1998: PKCS #1 v 2. 0 – adds RSA-OAEP encryption scheme • (M. Bellare and P. Rogaway, Eurocrypt ’ 94) • Sept. 1999: PKCS #1 v 2. 1 draft 1 – adds RSA-PSS signature scheme • (M. Bellare and P. Rogaway, Eurocrypt ’ 96)

History of PKCS #1 (cont’d) • July 2000: PKCS #1 v 2. 0 Amd. 1 – adds “multi-prime” RSA • soon: PKCS #1 v 2. 1 draft 2 – updates RSA-PSS to align with related standards • (for a preview, see IEEE P 1363 a D 5)

What is PSS? • PSS stands for Probabilistic Signature Scheme • Published in 1996 by M. Bellare and P. Rogaway • “Encoding method” for signatures with appendix in the integer factorization (IF) family, including RSA signatures • Provable security in the random oracle model • PSS-R variant provides message recovery

General Model for Signature Schemes • Following IEEE P 1363 classification • Primitives are mathematical operations on integers, field elements • Schemes are sets of operations on messages • Schemes are built up from primitives, “encoding methods” mapping between messages, integers – Note: in PKCS #1 v 2. 1 encoding methods map to strings, which are then converted to integers; this detail omitted here for simplicity

IF Family • Cryptography based on the difficulty of the integer factorization (IF) problem • Modulus n = pq • Public exponent e, private exponent d • RSA: e odd • Rabin-Williams: e even; conditions on p, q

Notation M message (string) m message representative (integer) s signature (integer) SP Signature Primitive (m s) VP Verification Primitive (s m)

Encoding Methods • Mappings between message M, integer message representative m – Encode: M m – Check: M, m consistent? – Decode: m M • Security goals: one-way, collision-resistant, no mathematical structure

IF Signature and Verification Primitives • RSA case: – SP: s = md mod n – VP: m = se mod n • Rabin-Williams case: – SP: s = |td mod n| • where t = m or m/2 such that (t/n) = +1 – VP: m = t, 2 t, n-t or 2(n-t) • where t = se mod n, m has redundancy

IF Signature Scheme with Appendix • Signature operation: – m = Encode(M) – s = SP(m) • Verification operation: – m = VP(s) – Check(M, m)

IF Signature Scheme with Message Recovery • Signature operation: – m = Encode(M) – s = SP(m) • Recovery operation: – m = VP(s) – M = Decode(m) • (Size of M is limited)

Draft Specification of PSS • RSASSA-PSS in PKCS #1 v 2. 1 d 2 – “RSA signature scheme with appendix based on PSS” • Follows general model, with new encoding operation • Aligned with IEEE P 1363 a D 5

PSS Encoding Method • Message representative is roughly same length as modulus • Based on underlying hash function, mask generation function

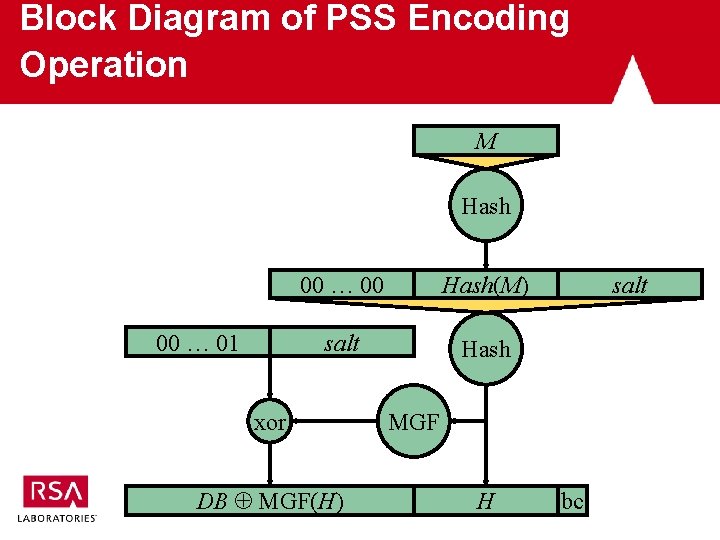
PSS Encoding Operation (Some Details Omitted) m = PSS-Encode (M) 1. Generate random salt 2. Hash message and salt, with some padding: H = Hash (00 … 00 || Hash (M) || salt) 3. Add padding to salt to form data block: DB = 00 … 01 || salt 4. Mask data block: masked. DB = DB xor MGF(H) 5. Format message representative: m = masked. DB || H || bc 16

PSS Checking Operation (Some Details Omitted) PSS-Check (M, m) 1. Parse message representative: masked. DB || H || bc 16 = m 2. Unmask data block: DB = masked. DB xor MGF(H) 3. Remove padding from data block to recover salt: 00 … 01 || salt = DB 4. Rehash message and salt and compare: H =? Hash (00 … 00 || Hash (M) || salt)

Block Diagram of PSS Encoding Operation M Hash 00 … 01 00 … 00 Hash(M) salt Hash xor DB MGF(H) salt MGF H bc

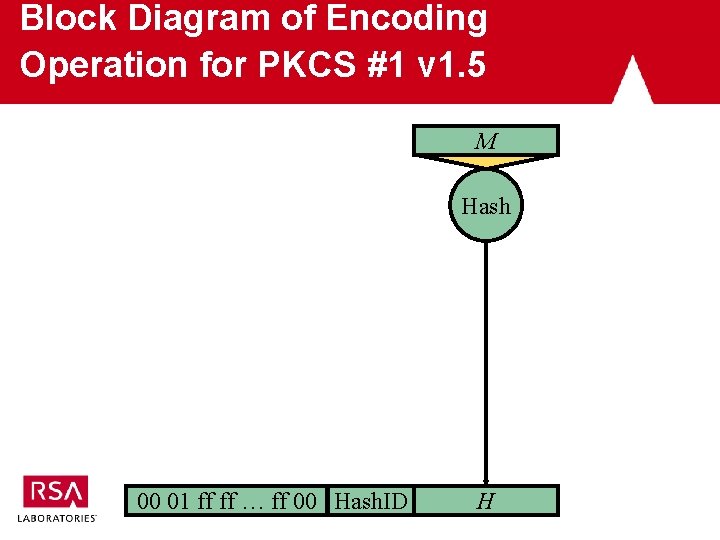
Block Diagram of Encoding Operation for PKCS #1 v 1. 5 M Hash 00 01 ff ff … ff 00 Hash. ID H

Observations • Message is hashed with random salt – improves security proof, resistance to fault analysis attacks • Salt value is included in data block – shortens signature overhead – for message recovery, part of message can be included • Data block is masked – randomizes input to primitive – removes multiplicative structure

Observations (cont’d) • Message representative ends with bc 16 – per ISO/IEC 9796 -2 format, to support RW primitive – but note that hash function identifier, header bits are not taken from that format • security proof would be “looser” • hash function ID turns out to be only partially helpful in variant with message recovery (a long story …)

Two-Level Hashing • In PKCS #1 v 2. 1 d 1 as well as the original PSS, message and salt were concatenated then hashed • Here, message hash is concatenated with salt • Motivation: – typical protocols hash message first, so integration of new method is easier – “single-pass” processing is easier, since salt is not needed until after message is hashed • Security proof is the same, under usual assumptions about hash function – proof holds even if attacker controls hash value

What’s Provable? • Suppose an algorithm A can forge PSS signatures without access to the details of Hash, MGF – Hash, MGF are effectively “random oracles” that can only be queried • Then an algorithm B can invert RSA in about the same time using algorithm A as a subroutine • If RSA is hard to invert, then PSS is secure against generic attacks

Proof Method • Inverting algorithm B “builds” Hash, MGF that appear random to forgery algorithm A, but embed an instance to be inverted • When A succeeds at forgery, B succeeds at inverting RSA • Random salt is key to “tight” proof; if not random, “looser” proof holds

What about the Random Oracle Model? • Some concerns have been raised about the relevance of proofs in the random oracle model: – some on theoretical grounds – others on practicality of “instantiating” a random oracle with a real hash or mask generation function • But although the proof may “overestimate” the properties of Hash and MGF, it underestimates properties of RSA – e. g. , bit security properties are not considered • Thus, in practice, PSS may well provide high security even without the random oracle model

ASN. 1 Syntax for RSASSA-PSS • Generic OID: – id-RSASSA-PSS : : = pkcs-1. 10 • Parameters: – RSASSA-PSS-params : : = SEQUENCE { hash. Func [0] Algorithm. Identifier {{oaep. Digest. Algorithms}} DEFAULT sha 1 Identifier, mask. Gen. Func [1] Algorithm. Identifier {{pkcs 1 MGFAlgorithms}} DEFAULT mgf 1 SHA 1 Identifier } • (For S/MIME, perhaps a separate OID for the steps after the message is hashed)

Patent Issues • University of California has applied for a patent (U. S. only) on PSS and PSS-R • In a letter to IEEE P 1363, UC has offered to waive licensing on PSS for signatures with appendix if adopted as an IEEE standard – agreed for ANSI X 9 F 1, ISO/IEC, NESSIE as well • Reasonable and non-discriminatory licensing for signatures with message recovery

Recommended Deployment • A gradual transition to PSS is recommended in the interest of prudent security – rollover, along with AES, new hash functions, … • PKCS #1 v 1. 5 signature scheme is still appropriate for new applications • Different than situation with PKCS #1 v 1. 5 encryption scheme, where only OAEP is recommended for new applications

Related Standards Work • IEEE P 1363 a will include PSS, PSS-R – also PKCS #1 v 1. 5 signatures • ANSI X 9. 31 expected to be revised to include PSS • ISO/IEC 9796 -2 working draft includes PSS-R • NESSIE submission prepared by RSA Laboratories • Significant coordination already; meetings of relevant groups over next two months

Questions from Last Year’s Workshop • PSS-R • ANSI X 9. 31 encoding method • Composite hash functions • New mask generation functions • Rabin-Williams support

PSS-R • Should PKCS #1 v 2. 1 include the PSS-R encoding method for signatures with message recovery? • ISO/IEC 9796 -2 is being updated to include PSS-R • PSS-R to be included in IEEE P 1363 a • Current answer: No

ANSI X 9. 31 Encoding Method • Should PKCS #1 v 2. 1 include the ANSI X 9. 31 encoding method? • ANSI X 9. 31 is a banking standard • FIPS 186 -2 supports it • Current answer: No

Composite Hash Functions • Should PKCS #1 v 2. 1 specify “composite” hash functions? – raised by Tom Gindin, IBM • Example: – SHA-1 -MD 5(M) = SHA-1(M) || MD 5(M) • A simple method to increase security in a modular fashion • Could be combined with PKCS #1 v 1. 5 encoding method, or PSS • Current answer: Maybe

New Mask Generation Functions • Should PKCS #1 v 2. 1 define new mask generation functions? • Example: – MGF 2(Z) = HMAC(Z, 0) || HMAC(Z, 1) || … • Current method lacks HMAC’s security proof: – MGF 1(Z) = Hash(0 || Z) || Hash(1 || Z) || … • Current answer: No

Rabin-Williams Support • Should PKCS #1 v 2. 1 include the RW primitives for even exponents? • Would be consistent with ANSI X 9. 31, X 9. 44 draft, IEEE P 1363 • PKCS #1 v 1. 5, PSS versions require slightly different primitives than currently specified – cf. relevant submissions to IEEE P 1363 a • Current answer: No

Conclusions • New version of PKCS #1 in development • Standards strategy for RSA signatures emerging – PSS a prudent choice for long-term security, harmonization of standards • For future work? – PKCS #1 usage guidelines – key generation and validation specifications

For More Information • PKCS #1 drafts: www. rsalabs. com/pkcs/ • IEEE P 1363 a drafts: grouper. ieee. org/groups/1363/ • bkaliski@rsasecurity. com