PITGORAS ALGO DE HISTORIA Pitgoras de Samos fue

PITÁGORAS

ALGO DE HISTORIA Pitágoras de Samos fue un filósofo y matemático griego que vivió entre los años 585 y 500 antes de nuestra era. Fundó la Escuela Pitagórica, una especie de secta cuyo símbolo era el pentágono estrellado, y que se dedicaba al estudio de la Filosofía, la Matemática y la Astronomía.

ALGO DE HISTORIA Durante muchos años se le ha atribuido a Pitágoras el enunciado y demostración del teorema geométrico que lleva su nombre. Sin embargo existen evidencias de que en otras culturas anteriores también se conocía el teorema, aunque de forma práctica.

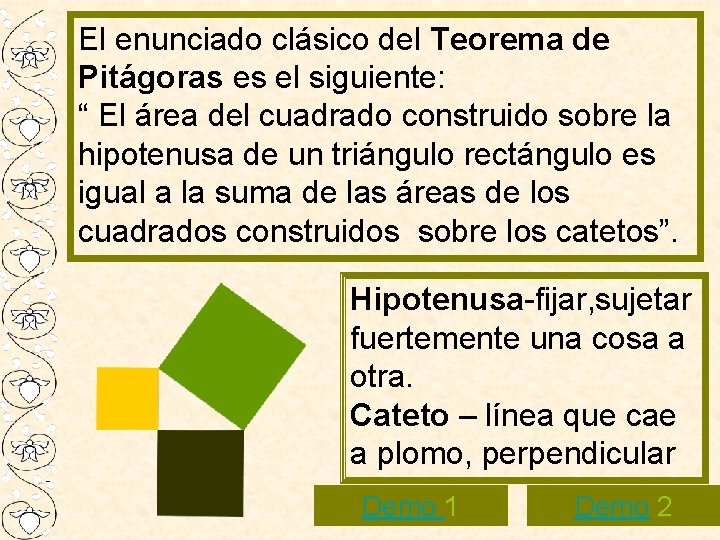
El enunciado clásico del Teorema de Pitágoras es el siguiente: “ El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo es igual a la suma de las áreas de los cuadrados construidos sobre los catetos”. Hipotenusa-fijar, sujetar fuertemente una cosa a otra. Cateto – línea que cae a plomo, perpendicular Demo 1 Demo 2

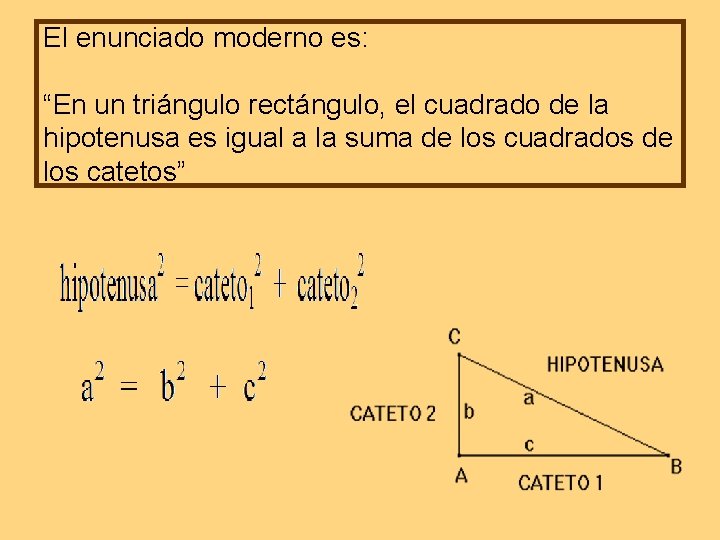
El enunciado moderno es: “En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”

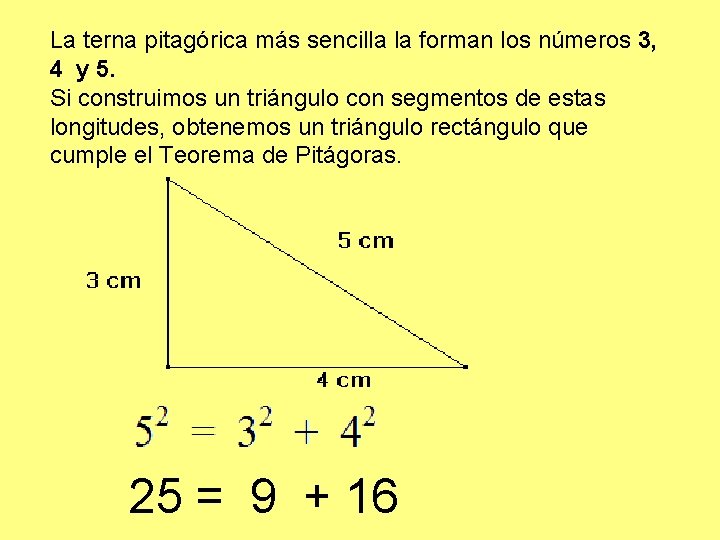
La terna pitagórica más sencilla la forman los números 3, 4 y 5. Si construimos un triángulo con segmentos de estas longitudes, obtenemos un triángulo rectángulo que cumple el Teorema de Pitágoras. 25 = 9 + 16

DEMOSTRACIÓN DE PITÁGORAS (siglo VI a. C. ) a. C Pitágoras había viajado a la antigua Babilonia y a Egipto donde posiblemente conoció la propiedad que verifican los lados de un triángulo rectángulo. En una tablilla de arcilla procedente de Babilonia conocida por PLIMPTON 322 y fechada en el 1900 a. C. aparecen, colocadas en columnas, ternas de números que verifican el teorema de Pitágoras son las llamadas "TERNAS PITAGÓRICAS".

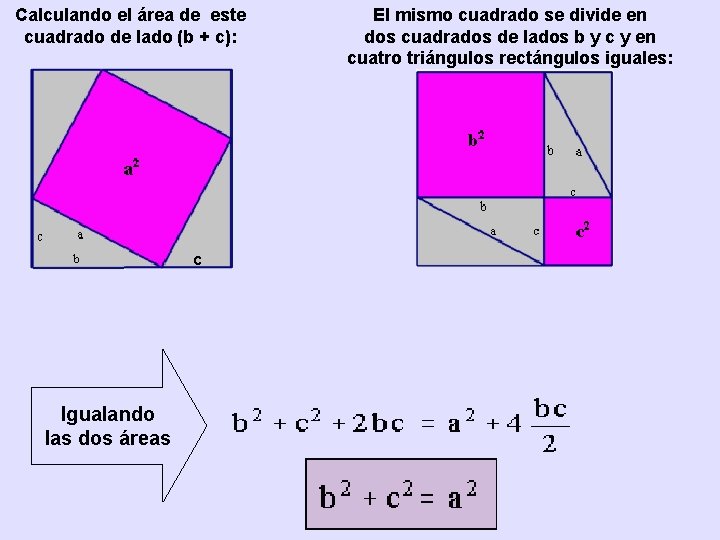
Calculando el área de este cuadrado de lado (b + c): c Igualando las dos áreas El mismo cuadrado se divide en dos cuadrados de lados b y c y en cuatro triángulos rectángulos iguales:

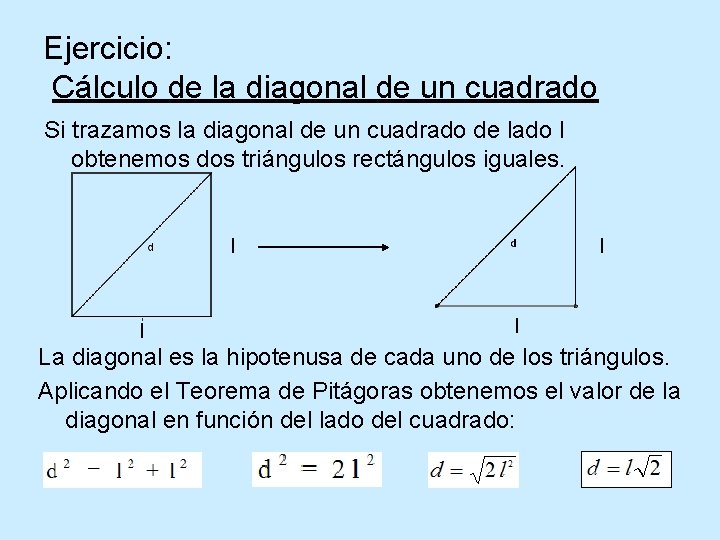
Ejercicio: Cálculo de la diagonal de un cuadrado Si trazamos la diagonal de un cuadrado de lado l obtenemos dos triángulos rectángulos iguales. l l La diagonal es la hipotenusa de cada uno de los triángulos. Aplicando el Teorema de Pitágoras obtenemos el valor de la diagonal en función del lado del cuadrado:

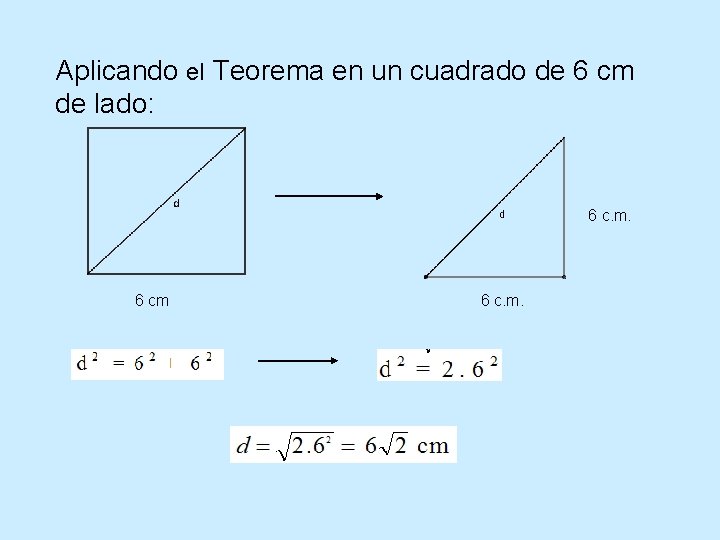
Aplicando el Teorema en un cuadrado de 6 cm de lado: 6 c. m. 6 cm 6 c. m.

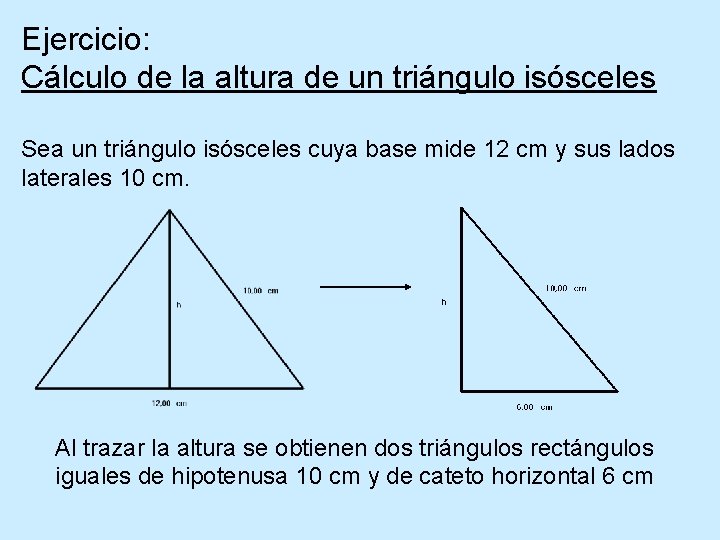
Ejercicio: Cálculo de la altura de un triángulo isósceles Sea un triángulo isósceles cuya base mide 12 cm y sus lados laterales 10 cm. Al trazar la altura se obtienen dos triángulos rectángulos iguales de hipotenusa 10 cm y de cateto horizontal 6 cm

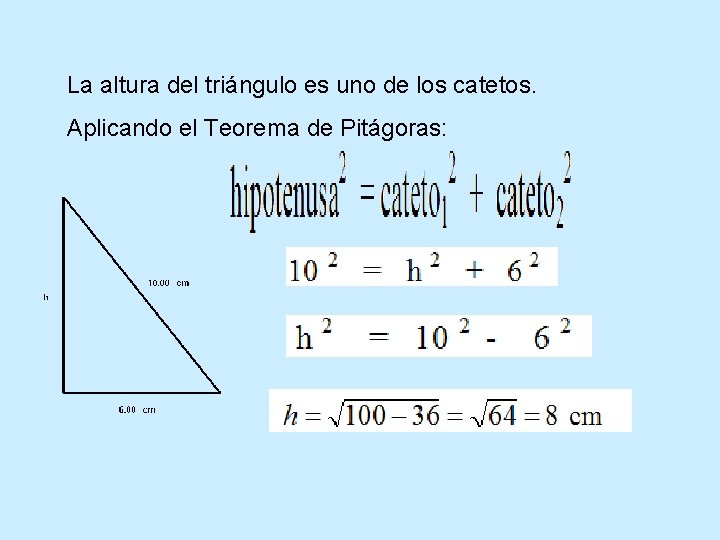
La altura del triángulo es uno de los catetos. Aplicando el Teorema de Pitágoras: