Pitanje br 35 Rotacija oko nepokretne ose i

Pitanje br. 35 Rotacija oko nepokretne ose i moment inercije Kruto telo učvršćeno u dve tačke O i O 1 se obrće oko nepokretne ose OO 1. Odrediti zakon kretanja tela: Kretanje oko ose Oz odredjeno je jnom:


Rotacija tela oko nepomične ose i moment inercije Sila se može razložiti na normalnu i trangencijalnu komponentu: Pod dejstvom tangencijalne komponente telo dobija ugaono ubrzanje: Odgovarajući moment sile iznosi: Moment inercije u odnosu na osu rotacije OO 1 Ugaono ubrzanje proporcionalno je momentu sila, a obrnuto proporcionalno momentu inercije.


Ako je tada je Odredjivanje momenta inercije tela Za izračunavanje momenta inercije neophodno je poznavanje ose rotacije i rasporeda masa u odnosu na osu rotacije. Za homogeno telo:
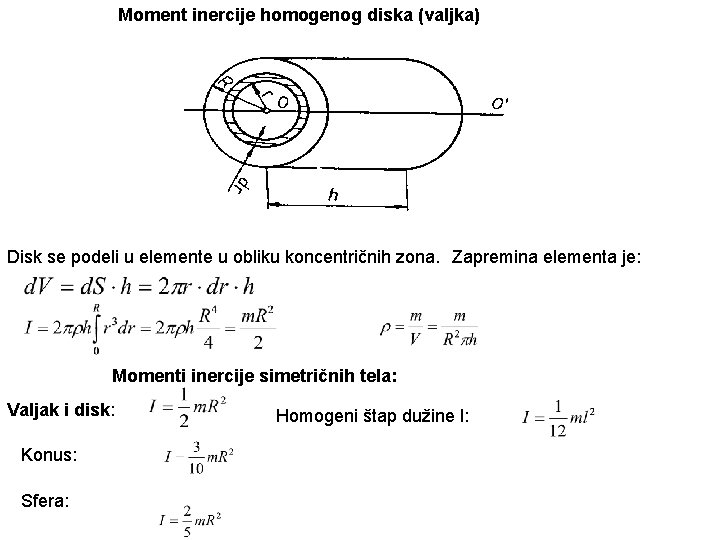
Moment inercije homogenog diska (valjka) Disk se podeli u elemente u obliku koncentričnih zona. Zapremina elementa je: Momenti inercije simetričnih tela: Valjak i disk: Konus: Sfera: Homogeni štap dužine l:

Pitanje br. 36 Štajnerova (Steiner) teorema Kada se izabrana osa rotacije ne poklapa sa osom simetrije, primenjuje se Štajnerova teorema za izračunavanje momenta inercije. Moment inercije u odnosu na proizvoljnu osu se može izračunati ako se zna njegov moment inercije oko paralelne ose koja prolazi kroz centar masa C. Primenom kosinusne teoreme dobija se: Moment inercije u odnosu na osu A: Moment inercije celog tela: Jer je

Štajnerova teorema: moment inercije krutog tela oko proizvoljne ose jednak je zbiru momenta oko paralelne ose koja prolazi kroz centar masa i proizvoda mase tela i kvadrata rastojanja izmedju osa. Složeno kretanje krutog tela može se razložiti na translatorno kretanje njegovog centra masa i na trenutno rotaciono kretanje oko tog centra. Položaj proizvoljne tačke m u odnosu na inercijalni sistem O´:


Pitanje br. 37 Rad, snaga i kinetička energija krutog tela Rad Pri rotaciji tela oko nepokretne ose, na svaku elementarnu masu, deluje spoljašnja sila i prelazi put: Rad spoljašnje sile je: Sabiranjem za sve elementarne mase tela: Integraljenjem se dobija rad spoljašnjih sila: Ako je momrnt sile Mz=const.


Snaga tela koje rotira brojno je jednaka skalarnom proizvodu momenta spoljašnjih sila i ugaone brzine Kinetička energija Svaki element zbog periferne brzine ima kinetičku energiju Jer je Kinetička energija je aditivna veličina: kinetička energija tela koje rotira oko ose Oz Rotacija oko paralelne ose AA´:

Složeno kretanje Kinetička energija: jer je Pošto se O poklapa sa centrom masa rc=0 =zbiru kin en transl kretanja centra masa I energije rotacije

Rotacija tela oko slobodne ose Ako telo rotira oko proizvoljne ose i prepusti se samom sebi, položaj ose se menja. Dejstvom centrifugalne sile osa se krivi. Ako osa prolazi kroz centar masa sile se uravnotežavaju (c). Osa rotacije čiji se položaj održava u prostoru je slobodna osa. Glavne ose inercije-3 medj normalne ose koje prolaze kroz CM. Ose simetrije-za pravilna geom tela


Tela pri stabilnoj rotaciji teže da zadrže stalnu orijentaciju ose rotacije u prostoru. (posledica zakona održanja momenta impulsa-stbilna rotacija oko ose sa najvećim momentom inercije) a) b) Rotacija oko slobodne ose –Kardanov zglob (b)

Pitanje br. 38 Čigra je simetrično kruto telo koje se obrće velikom brzinom oko slobodne ose simetrije čija je jedna tačka oslonac. Oslonac je ispod centra masa

Težina čigre svojom normalnom komponentom deluje momentom, koji se nalazi u horizontalnoj ravni i obrće se zajedno sa osom čigre. Intenzitet momenta sile je: Stalno dejstvo momenta M izaziva priraštaj momenta impulsa: Vektor momenta impulsa ima stalan intenzitet, a menja se po pravcu, zajedno sa osom čigre koja opisuje konusnu površinu sa vrhom u tački oslonca. Kretanje pravca momenta impulsa (i ose ) naziva se precesija. Ugaona brzina precesije čigre

Statika je deo mehanike koja proučava uslove relativnog mirovanja. Uslovi relativnog mirovanja materijalne tačke Uslovi s eodredjuju iz njene jednačine kretanja R je rezultanta svih spoljašnjih sila koje deluju na telo. Projekcije na ose Oxyz su: a) b )

Uslovi relativnog mirovanja krutog tela Kruto telo je u stanju relativnog mirovanja ako su ispunjeni uslovi da ne vrši translatorno (a) i rotaciono (b) kretanje a) b) i
- Slides: 20