Pitagora e Euclide Giochi matematici con triangoli quadrati

“Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” Nando Geronimi Milano - 4 ottobre 2014 PARIGI 2014

“Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” Nando Geronimi Milano - 4 ottobre 2014 "Giochi, Modelli, Storia“ Milano 3 -4 -5 ottobre 2013

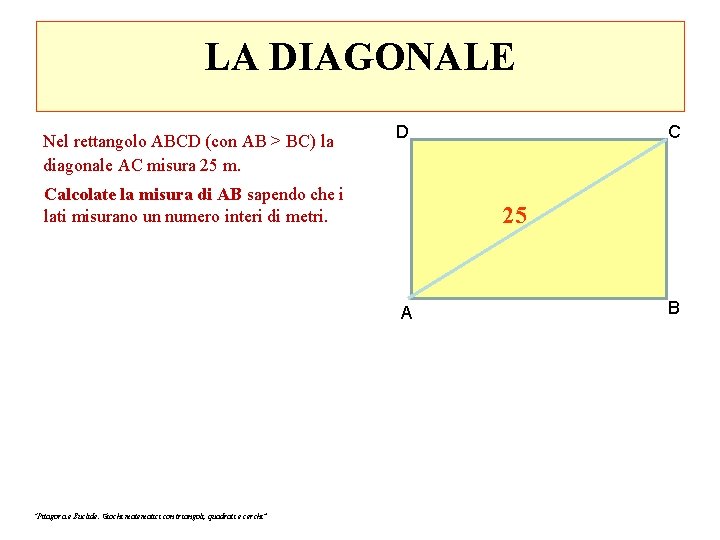
LA DIAGONALE Nel rettangolo ABCD (con AB > BC) la diagonale AC misura 25 m. D Calcolate la misura di AB sapendo che i lati misurano un numero interi di metri. 25 A “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” C B

TERNA PITAGORICA Una terna pitagorica è una terna di numeri interi positivi a, b, c tali che: a 2 + b 2 = c 2 La prima e più conosciuta terna pitagorica (ridotta) è: 3, 4, 5 perché 32 + 42 = 52 Una seconda terna pitagorica (ridotta) è: 5, 12, 13 perché 52+122=132 Da ogni terna pitagorica ridotta del tipo a, b, c si ricavano infinite altre terne pitagoriche (derivate) moltiplicando ogni numero per un fattore k intero positivo: ka, kb, kc “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

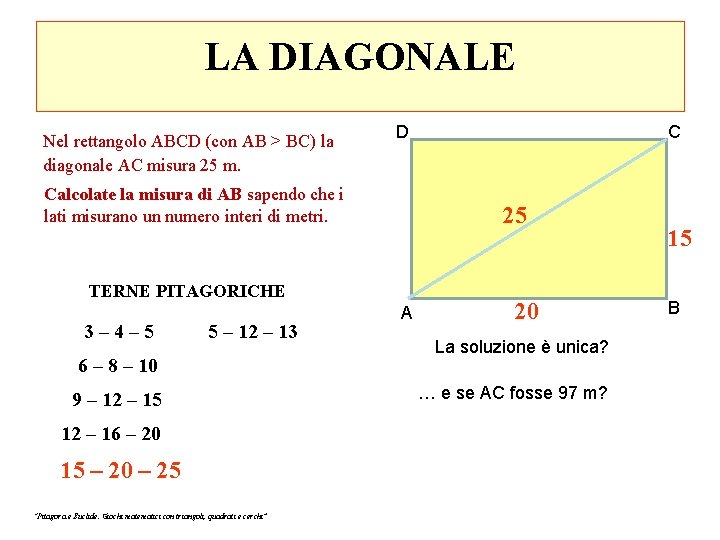
LA DIAGONALE Nel rettangolo ABCD (con AB > BC) la diagonale AC misura 25 m. D Calcolate la misura di AB sapendo che i lati misurano un numero interi di metri. 25 TERNE PITAGORICHE 3 – 4 – 5 5 – 12 – 13 6 – 8 – 10 9 – 12 – 15 12 – 16 – 20 15 – 20 – 25 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” C A 20 La soluzione è unica? … e se AC fosse 97 m? 15 B

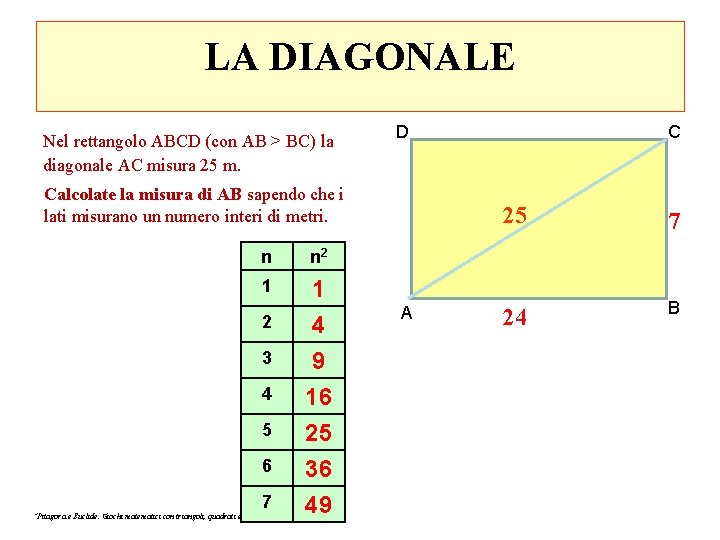
LA DIAGONALE Nel rettangolo ABCD (con AB > BC) la diagonale AC misura 25 m. D Calcolate la misura di AB sapendo che i lati misurano un numero interi di metri. n n 2 1 1 4 9 16 25 36 49 2 3 4 5 6 7 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” A C 25 7 24 B

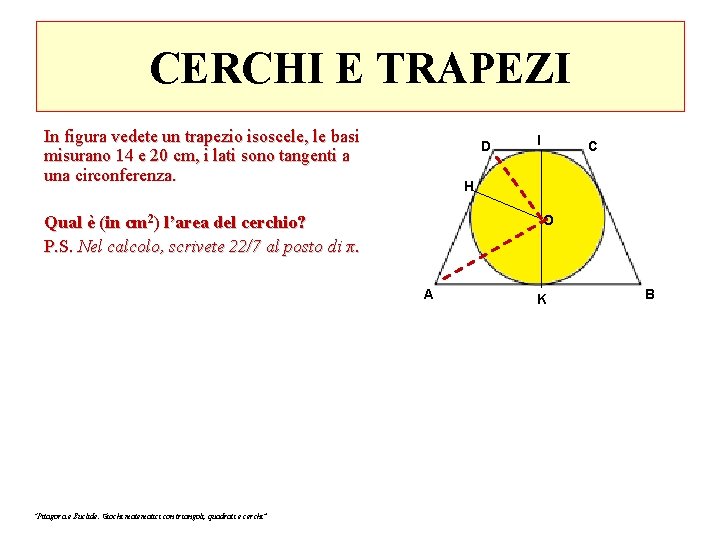
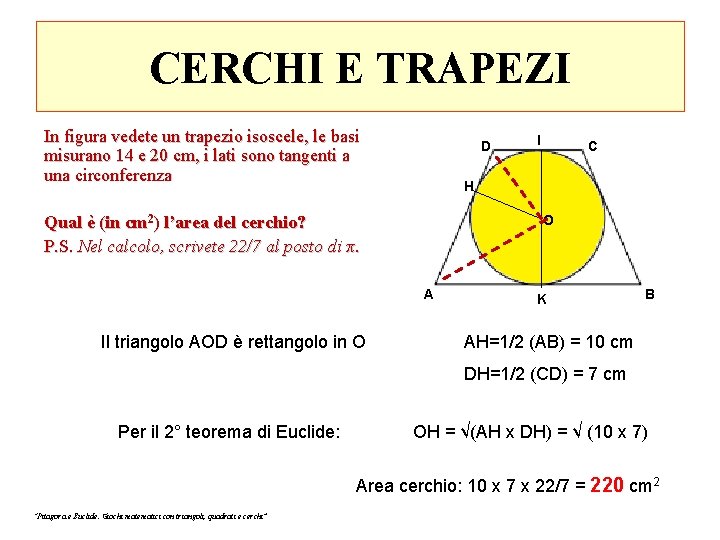
CERCHI E TRAPEZI In figura vedete un trapezio isoscele, le basi misurano 14 e 20 cm, i lati sono tangenti a una circonferenza. D C H O Qual è (in cm 2) l’area del cerchio? P. S. Nel calcolo, scrivete 22/7 al posto di π. A “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” I K B

CERCHI E TRAPEZI In figura vedete un trapezio isoscele, le basi misurano 14 e 20 cm, i lati sono tangenti a una circonferenza D C H O Qual è (in cm 2) l’area del cerchio? P. S. Nel calcolo, scrivete 22/7 al posto di π. A Il triangolo AOD è rettangolo in O I K B AH=1/2 (AB) = 10 cm DH=1/2 (CD) = 7 cm Per il 2° teorema di Euclide: OH = √(AH x DH) = √ (10 x 7) Area cerchio: 10 x 7 x 22/7 = 220 cm 2 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

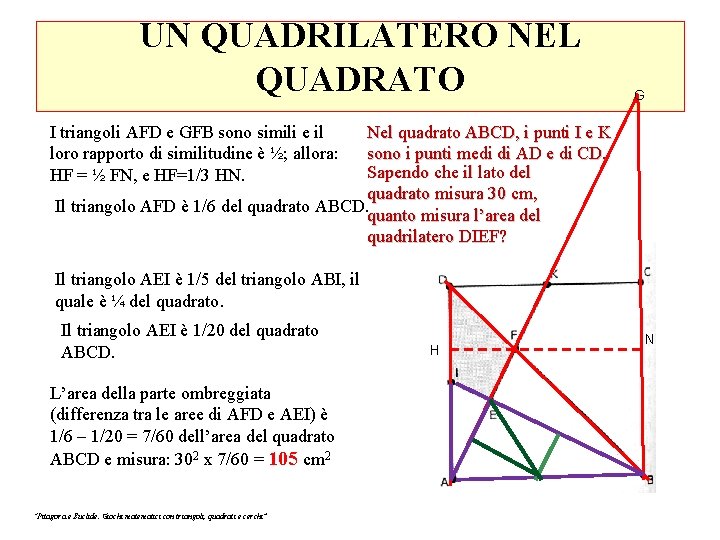
UN QUADRILATERO NEL QUADRATO G I triangoli AFD e GFB sono simili e il loro rapporto di similitudine è ½; allora: HF = ½ FN, e HF=1/3 HN. Nel quadrato ABCD, i punti I e K sono i punti medi di AD e di CD. Sapendo che il lato del quadrato misura 30 cm, Il triangolo AFD è 1/6 del quadrato ABCD. quanto misura l’area del quadrilatero DIEF? Il triangolo AEI è 1/5 del triangolo ABI, il quale è ¼ del quadrato. Il triangolo AEI è 1/20 del quadrato ABCD. L’area della parte ombreggiata (differenza tra le aree di AFD e AEI) è 1/6 – 1/20 = 7/60 dell’area del quadrato ABCD e misura: 302 x 7/60 = 105 cm 2 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” H N

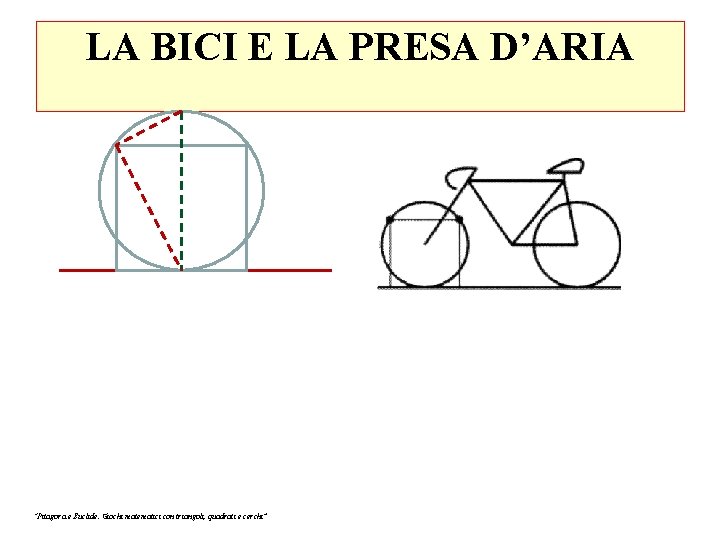
LA BICI E LA PRESA D’ARIA Una bicicletta è accuratamente appoggiata ad un muro. In questo muro, a livello del suolo, si trova una presa d’aria quadrata. Curiosamente i due angoli superiori della presa d’aria, coincidono con due punti della ruota, come indicato nella figura. Sapendo che il lato della presa d’aria misura 56 cm, quanto misura il diametro della ruota della bicicletta? Dare la risposta in centimetri, arrotondando eventualmente al centimetro più vicino. “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

LA BICI E LA PRESA D’ARIA “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

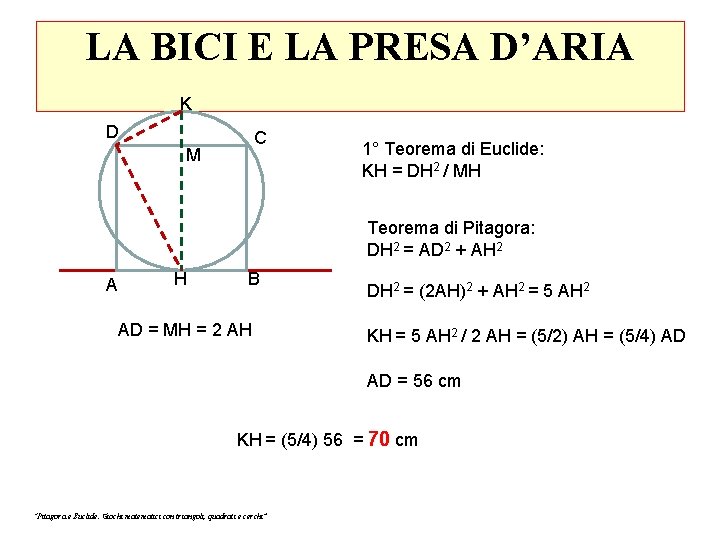
LA BICI E LA PRESA D’ARIA K D C M 1° Teorema di Euclide: KH = DH 2 / MH Teorema di Pitagora: DH 2 = AD 2 + AH 2 A H B AD = MH = 2 AH DH 2 = (2 AH)2 + AH 2 = 5 AH 2 KH = 5 AH 2 / 2 AH = (5/2) AH = (5/4) AD AD = 56 cm KH = (5/4) 56 = 70 cm “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

L’EREDITA’ (Finale nazionale 2014) Amerigo e Renato hanno ricevuto in eredità il terreno che vedete in figura. È una buona eredità, anche se il perimetro non raggiunge i 10. 000 decimetri. Si sono allora diviso il terreno in due parti che hanno, ciascuna, la forma di un triangolo rettangolo; il lato comune ha una lunghezza di 2014 dm e la misura di ogni lato è espressa da un numero intero di dm. Qual è esattamente il perimetro dell’intero terreno? “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” C 2014 D A B

TERNA PITAGORICA Una terna pitagorica è una terna di numeri interi positivi a, b, c tali che a 2 + b 2 = c 2 Quante terne pitagoriche si conoscono? Scrivete due numeri m e n interi positivi (m>n) Calcolate: a: m 2 – n 2 b: 2 mn c: m 2+n 2 Esempi: m=2, n=1 a: 22 – 12 = 3 b: 2 x 2 x 1 = 4 c: 22 + 12 = 5 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” Esempi: m=3, n=2 a: 32 – 22 = 5 b: 2 x 3 x 2 = 12 c: 32 + 22 = 13 Esempi: m=5, n=2 a: 52 – 22 = 21 b: 2 x 5 x 2 = 20 c: 52 + 22 = 29

L’EREDITA’ (Finale nazionale 2014) Amerigo e Renato hanno ricevuto in eredità il terreno che vedete in figura. È una buona eredità, anche se il perimetro non raggiunge i 10. 000 decimetri. Si sono allora diviso il terreno in due parti che hanno, ciascuna, la forma di un triangolo rettangolo; il lato comune ha una lunghezza di 2014 dm e la misura di ogni lato è espressa da un numero intero di dm. Qual è esattamente il perimetro dell’intero terreno? C 2014 = 2 x 53 x 19 2014 D B A AB = 532 -192=2809 -361= 2448 CB = 532+192=2809+361= 3170 2° triangolo rettangolo: ipotenusa=2014=2 x 19 x 53=2 x 19 x(49+4)=2 x 19 x(72+22), m=7, n=2 CD= 2 x 19 x(72 -22) = 2 x 19 x(49 -4) = 2 x 19 x 45=1710 AD= 2 x 19 x 2 x 7 x 2=1064 Perimetro = 2448+3170+1710+1064= 8392 dm 2 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

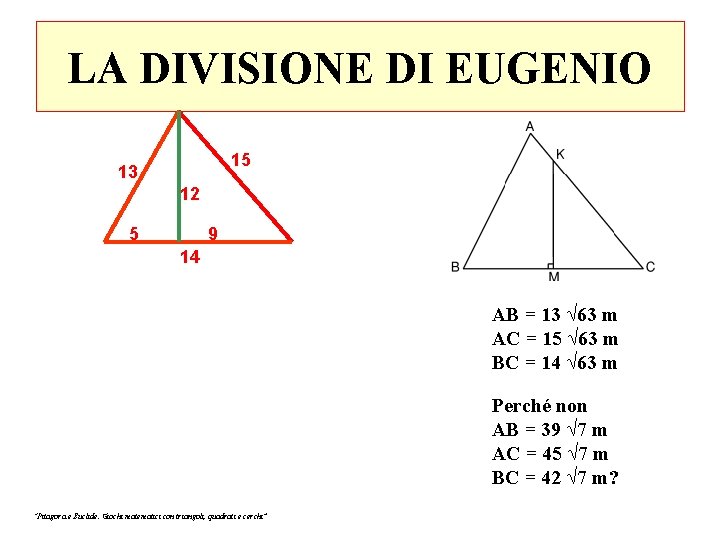
LA DIVISIONE DI EUGENIO Il grande architetto Eugenio Itor adorava i numeri interi. Ammiratore di Pitagora e Talete, acquistò il campo triangolare rappresentato in figura i cui lati misuravano, maliziosamente, AB = 13 √ 63 m, AC = 15 √ 63 m BC = 14 √ 63 m. Quando morì, i suoi due figli, Delim e Facil, si divisero il terreno in due parti aventi la stessa area. Delim e Facil decisero di costruire un muro di separazione rettilineo e perpendicolare al lato BC. Quanti metri misura, arrotondata al centimetro, la lunghezza del muro di separazione? Prendere 2, 646 per √ 7 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” AB = 13 √ 63 m AC = 15 √ 63 m BC = 14 √ 63 m

LA DIVISIONE DI EUGENIO 15 13 12 5 9 14 AB = 13 √ 63 m AC = 15 √ 63 m BC = 14 √ 63 m Perché non AB = 39 √ 7 m AC = 45 √ 7 m BC = 42 √ 7 m? “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

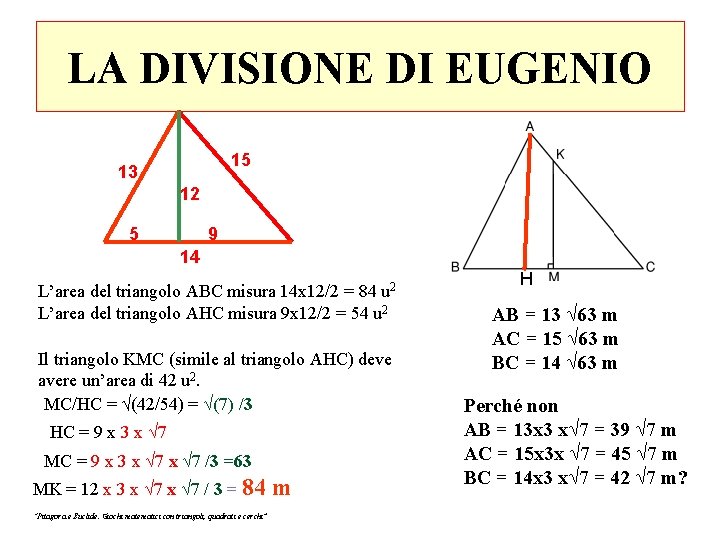
LA DIVISIONE DI EUGENIO 15 13 12 5 9 14 L’area del triangolo ABC misura 14 x 12/2 = 84 u 2 L’area del triangolo AHC misura 9 x 12/2 = 54 u 2 Il triangolo KMC (simile al triangolo AHC) deve avere un’area di 42 u 2. MC/HC = √(42/54) = √(7) /3 HC = 9 x 3 x √ 7 MC = 9 x 3 x √ 7 /3 =63 MK = 12 x 3 x √ 7 / 3 = 84 m “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” H AB = 13 √ 63 m AC = 15 √ 63 m BC = 14 √ 63 m Perché non AB = 13 x 3 x√ 7 = 39 √ 7 m AC = 15 x 3 x √ 7 = 45 √ 7 m BC = 14 x 3 x√ 7 = 42 √ 7 m?

TERNA PITAGORICA Scrivete due numeri a piacere. Scrivete poi un terzo numero uguale alla somma dei primi due. Scrivere ora un quarto numero uguale alla somma degli ultimi due Calcolate il prodotto tra il primo e il quarto. Calcolate il doppio prodotto tra il secondo e il terzo. Avete trovato i primi due numeri una terna pitagorica! Qual è il terzo numero? Il quadrato del secondo più il quadrato del terzo. Esempio: 2 x 8=16 1° numero: 2 162+302 = 342 2 x 3 x 5=30 2° numero: 3 32+52 = 34 3° numero: 5 4° numero: 8 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

TERNA PITAGORICA di FIBO La successione di Fibonacci: 1, 1, 2 , 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 ………. . Prendiamo 4 numeri consecutivi della successione. Esempio: 5, 8, 13, 21. Il prodotto tra il primo e il quarto numero: 5 x 21=105, il doppio prodotto tra il secondo e il terzo: 2 x 8 x 13=208 √(1052+2082) =√(11025+43264) = √ 54289) = 233 105, 208, 233 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

TERNA PITAGORICA di FIBO Una generica successione di Fibonacci: a, b, a+b, a+2 b, 2 a+3 b, 3 a+5 b, 5 a+8 b, 8 a+13 b, 13 a+21 b … Prendiamo i primi 4 numeri consecutivi della successione. a, b, a+b, a+2 b Il prodotto tra il primo e il quarto numero: a 2+2 ab il doppio prodotto tra il secondo e il terzo: 2 ab+2 b 2 sono i primi due termini di una terna pitagorica Il terzo numero è (a+b)2 +b 2 “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

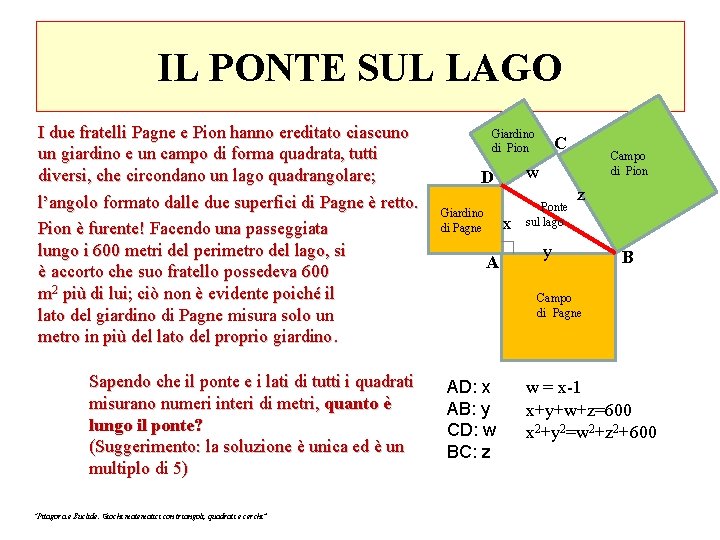
IL PONTE SUL LAGO I due fratelli Pagne e Pion hanno ereditato ciascuno un giardino e un campo di forma quadrata, tutti diversi, che circondano un lago quadrangolare; l’angolo formato dalle due superfici di Pagne è retto. Pion è furente! Facendo una passeggiata lungo i 600 metri del perimetro del lago, si è accorto che suo fratello possedeva 600 m 2 più di lui; ciò non è evidente poiché il lato del giardino di Pagne misura solo un metro in più del lato del proprio giardino. Sapendo che il ponte e i lati di tutti i quadrati misurano numeri interi di metri, quanto è lungo il ponte? (Suggerimento: la soluzione è unica ed è un multiplo di 5) “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” Giardino di Pion Giardino di Pagne Campo di Pion Ponte sul lago Campo di Pagne

IL PONTE SUL LAGO I due fratelli Pagne e Pion hanno ereditato ciascuno un giardino e un campo di forma quadrata, tutti diversi, che circondano un lago quadrangolare; l’angolo formato dalle due superfici di Pagne è retto. Pion è furente! Facendo una passeggiata lungo i 600 metri del perimetro del lago, si è accorto che suo fratello possedeva 600 m 2 più di lui; ciò non è evidente poiché il lato del giardino di Pagne misura solo un metro in più del lato del proprio giardino. Sapendo che il ponte e i lati di tutti i quadrati misurano numeri interi di metri, quanto è lungo il ponte? (Suggerimento: la soluzione è unica ed è un multiplo di 5) “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” Giardino di Pion x A Campo di Pion w D Giardino di Pagne C Ponte sul lago z y B Campo di Pagne AD: x AB: y CD: w BC: z w = x-1 x+y+w+z=600 x 2+y 2=w 2+z 2+600

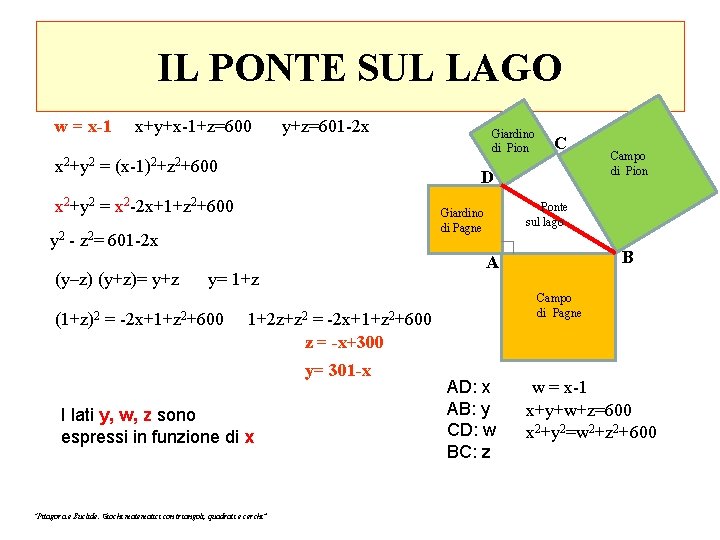
IL PONTE SUL LAGO w = x-1 x+y+x-1+z=600 y+z=601 -2 x x 2+y 2 = (x-1)2+z 2+600 Campo di Pagne 1+2 z+z 2 = -2 x+1+z 2+600 z = -x+300 y= 301 -x “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” B A y= 1+z Campo di Pion Ponte sul lago Giardino di Pagne y 2 - z 2= 601 -2 x (1+z)2 = -2 x+1+z 2+600 C D x 2+y 2 = x 2 -2 x+1+z 2+600 (y–z) (y+z)= y+z Giardino di Pion AD: x AB: y CD: w BC: z w = x-1 x+y+w+z=600 x 2+y 2=w 2+z 2+600

IL PONTE SUL LAGO w = x-1 x+y+x-1+z=600 y+z=601 -2 x x 2+y 2 = (x-1)2+z 2+600 Campo di Pagne 1+2 z+z 2 = -2 x+1+z 2+600 z = -x+300 y= 301 -x I lati y, w, z sono espressi in funzione di x “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” B A y= 1+z Campo di Pion Ponte sul lago Giardino di Pagne y 2 - z 2= 601 -2 x (1+z)2 = -2 x+1+z 2+600 C D x 2+y 2 = x 2 -2 x+1+z 2+600 (y–z) (y+z)= y+z Giardino di Pion AD: x AB: y CD: w BC: z w = x-1 x+y+w+z=600 x 2+y 2=w 2+z 2+600

IL PONTE SUL LAGO w = x-1 z = -x+300 Giardino di Pion x 2+y 2=n 2 C D y= 301 -x (Suggerimento: la soluzione è unica ed è un multiplo di 5) Campo di Pion Ponte sul lago Giardino di Pagne B A x, y, n è una terna pitagorica derivata da 3, 4, 5 ? Se si allora: y=4/3 x Campo di Pagne 4/3 x = 301 - x 7/3 x = 301 x = 129 = (3 x 43) y = 172 = (4 x 43) n = 215 = (5 x 43) w = 128 z = 171 Il ponte è lungo 215 metri “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

ARBELO La decorazione in legno che ricorda un arbelo, è stata ricavata da un semicilindro di diametro AB da cui sono stati tagliati due semicilindri di diametro AC e BC; il punto C divide AB in due parti tali che AC = 3 BC. Sapendo che il semicilidro originale pesava esattamente 8 kg, quanto pesa l’arbelo? L’arbelo che parte è del semicilindro? L’area dell’arbelo è equivalente all’area del cerchio che ha per diametro il segmento CD. Se AB= 8, allora AC=6, BC=2 e, per il 2° di Euclide, CD=2√ 3. Area semicilindro: 42π /2 = 8 π Area arbelo: 3 π L’arbelo è i 3/8 del semicilindro “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi” Se il semicilindro pesava 8 kg allora la decorazione pesa 3 kg.

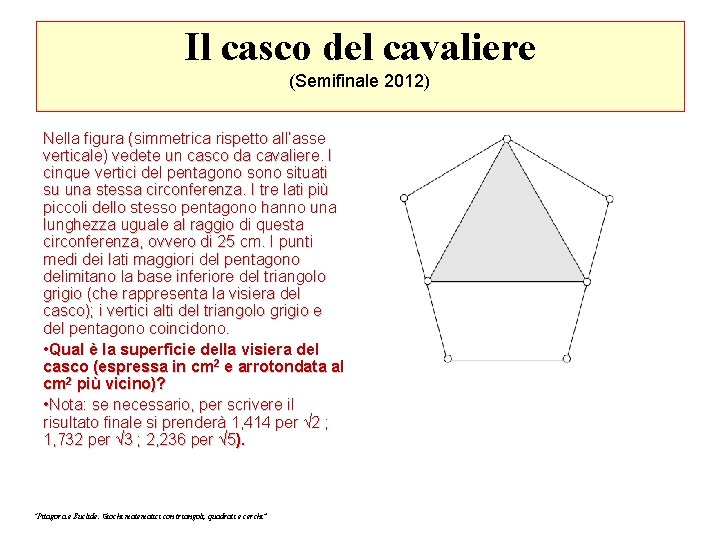
Il casco del cavaliere (Semifinale 2012) Nella figura (simmetrica rispetto all’asse verticale) vedete un casco da cavaliere. I cinque vertici del pentagono situati su una stessa circonferenza. I tre lati più piccoli dello stesso pentagono hanno una lunghezza uguale al raggio di questa circonferenza, ovvero di 25 cm. I punti medi dei lati maggiori del pentagono delimitano la base inferiore del triangolo grigio (che rappresenta la visiera del casco); i vertici alti del triangolo grigio e del pentagono coincidono. • Qual è la superficie della visiera del casco (espressa in cm 2 e arrotondata al cm 2 più vicino)? • Nota: se necessario, per scrivere il risultato finale si prenderà 1, 414 per √ 2 ; 1, 732 per √ 3 ; 2, 236 per √ 5). “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

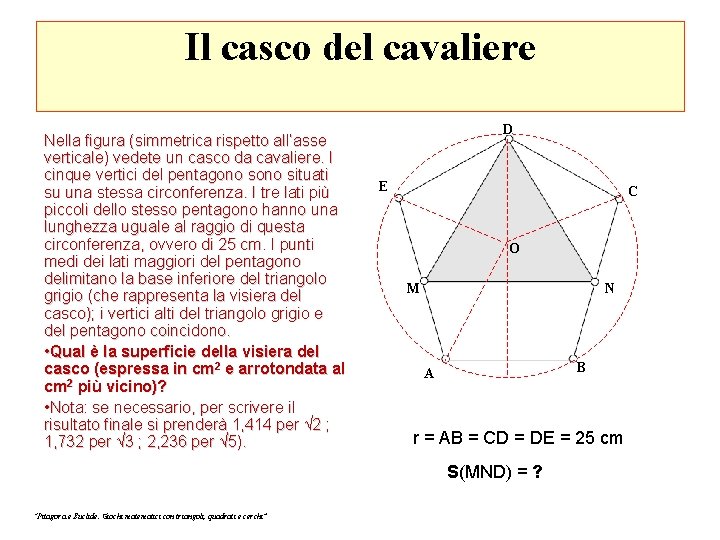
Il casco del cavaliere Nella figura (simmetrica rispetto all’asse verticale) vedete un casco da cavaliere. I cinque vertici del pentagono situati su una stessa circonferenza. I tre lati più piccoli dello stesso pentagono hanno una lunghezza uguale al raggio di questa circonferenza, ovvero di 25 cm. I punti medi dei lati maggiori del pentagono delimitano la base inferiore del triangolo grigio (che rappresenta la visiera del casco); i vertici alti del triangolo grigio e del pentagono coincidono. • Qual è la superficie della visiera del casco (espressa in cm 2 e arrotondata al cm 2 più vicino)? • Nota: se necessario, per scrivere il risultato finale si prenderà 1, 414 per √ 2 ; 1, 732 per √ 3 ; 2, 236 per √ 5). D E C O M N B A r = AB = CD = DE = 25 cm S(MND) = ? “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

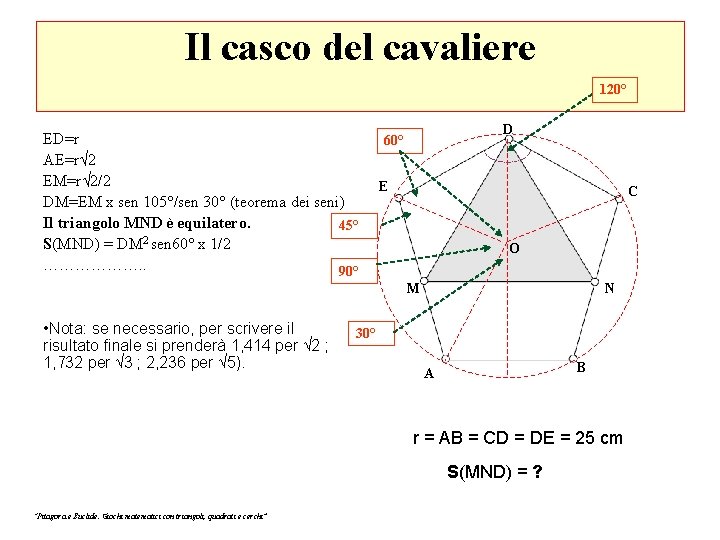
Il casco del cavaliere 120° ED=r AE=r√ 2 EM=r√ 2/2 DM=EM x sen 105°/sen 30° (teorema dei seni) Il triangolo MND è equilatero. 45° S(MND) = DM 2 sen 60° x 1/2 ………………. . 90° D 60° E C O M • Nota: se necessario, per scrivere il risultato finale si prenderà 1, 414 per √ 2 ; 1, 732 per √ 3 ; 2, 236 per √ 5). N 30° B A r = AB = CD = DE = 25 cm S(MND) = ? “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”

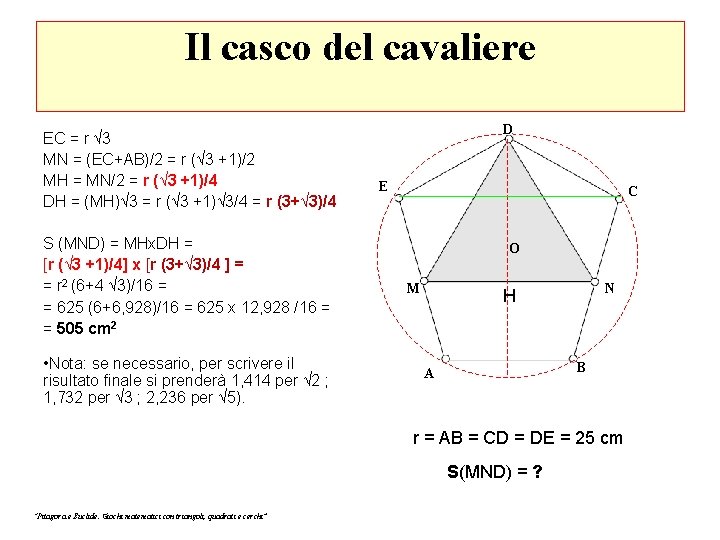
Il casco del cavaliere EC = r √ 3 MN = (EC+AB)/2 = r (√ 3 +1)/2 MH = MN/2 = r (√ 3 +1)/4 DH = (MH)√ 3 = r (√ 3 +1)√ 3/4 = r (3+√ 3)/4 S (MND) = MHx. DH = [r (√ 3 +1)/4] x [r (3+√ 3)/4 ] = = r 2 (6+4 √ 3)/16 = = 625 (6+6, 928)/16 = 625 x 12, 928 /16 = = 505 cm 2 • Nota: se necessario, per scrivere il risultato finale si prenderà 1, 414 per √ 2 ; 1, 732 per √ 3 ; 2, 236 per √ 5). D E C O M N H B A r = AB = CD = DE = 25 cm S(MND) = ? “Pitagora e Euclide. Giochi matematici con triangoli, quadrati e cerchi”