Piecewise Polynomial Spaces The reason for introducing a

Piecewise Polynomial Spaces The reason for introducing a mesh of a domain is that it allows for a construction of piecewise polynomial function spaces on this domain Definition: linear function in x and y Is a linear function in x and y Example:

Piecewise Polynomial Spaces Definition: triangle with nodes be the space of linear functions on is Remark: We observe that any member in uniquely determined by its nodal values Example: Find a linear polynomial triangle K such that p(N 1)=2 , p(N 2) = 3, p(N 3)=1 on the

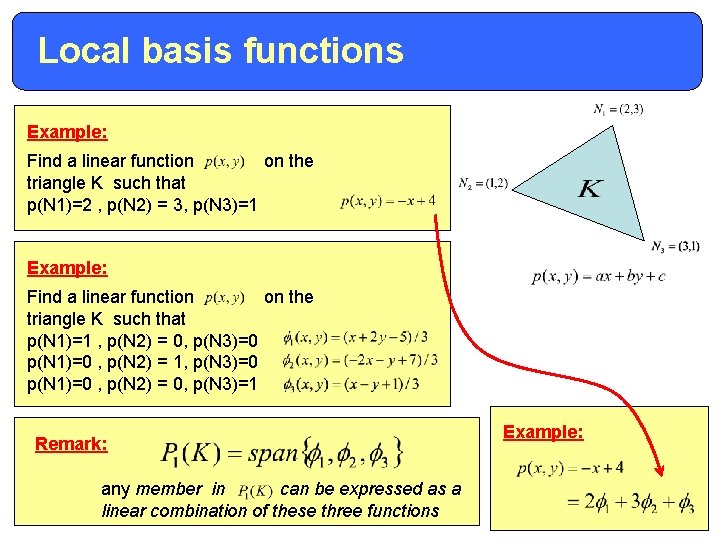
Local basis functions Example: Find a linear function on the triangle K such that p(N 1)=2 , p(N 2) = 3, p(N 3)=1 Example: Find a linear function on the triangle K such that p(N 1)=1 , p(N 2) = 0, p(N 3)=0 p(N 1)=0 , p(N 2) = 1, p(N 3)=0 p(N 1)=0 , p(N 2) = 0, p(N 3)=1 Remark: any member in can be expressed as a linear combination of these three functions Example:

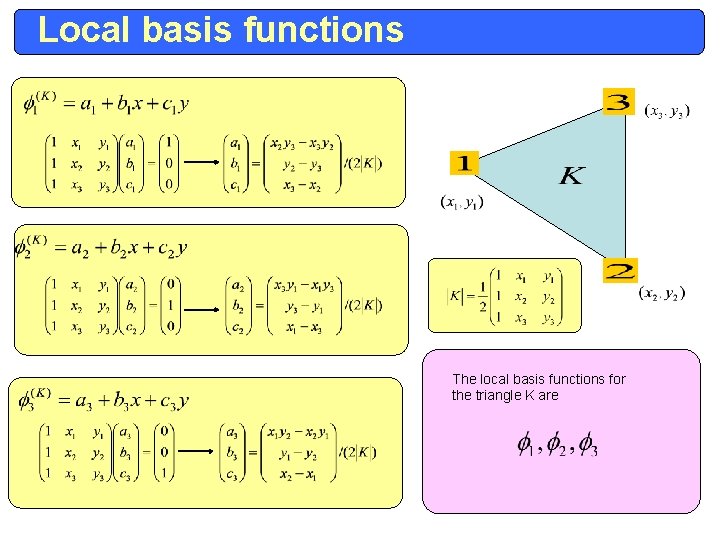
Local basis functions The local basis functions for the triangle K are

Local basis functions Exercise 3 Find three linear functions on the reference triangle such that Reference triangle Then find a linear function reference triangle K such that p(0, 0)=2 , p(1, 0) = 3, p(0, 1)=1 on the

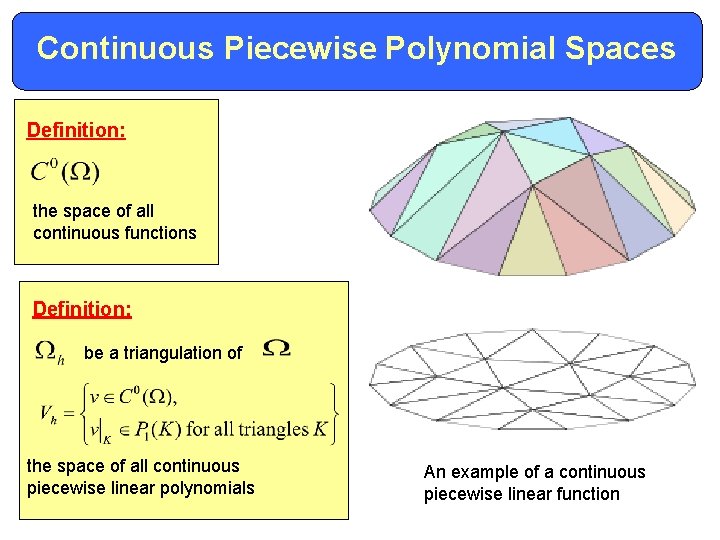
Continuous Piecewise Polynomial Spaces Definition: the space of all continuous functions Definition: be a triangulation of the space of all continuous piecewise linear polynomials An example of a continuous piecewise linear function

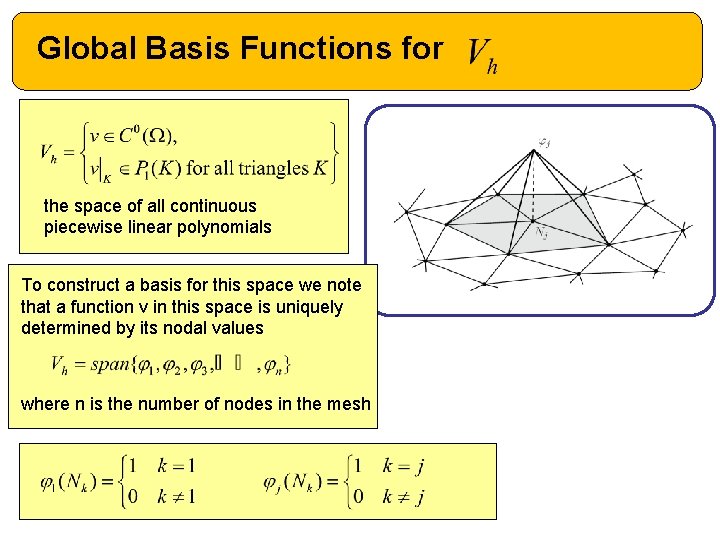
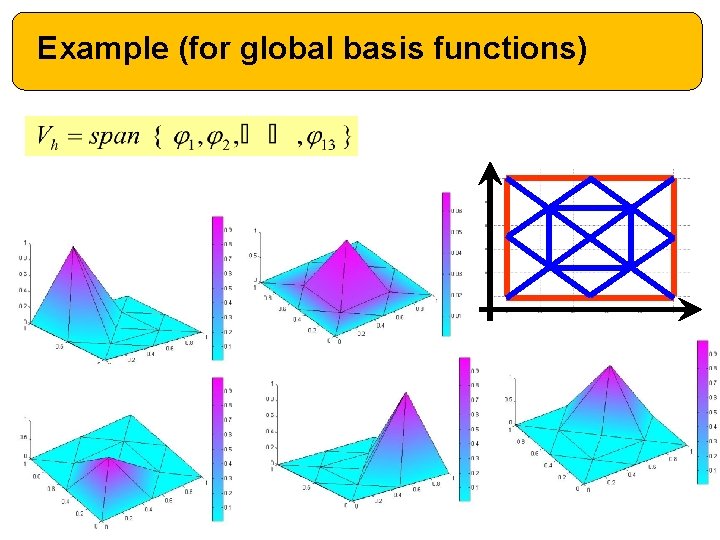
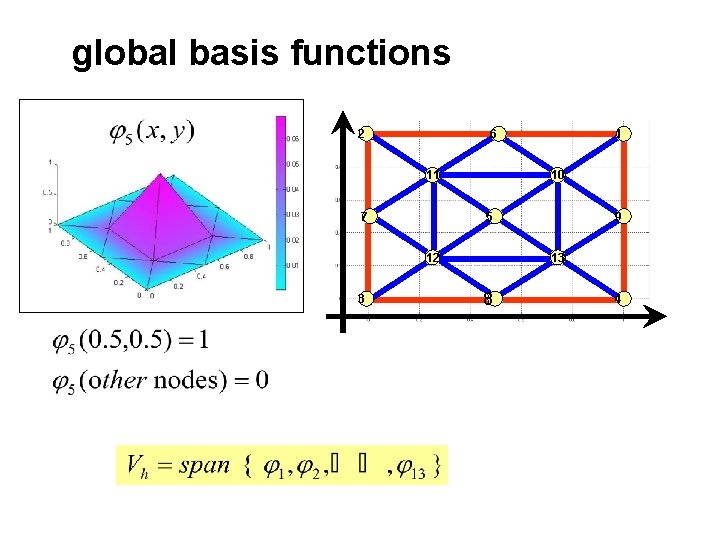
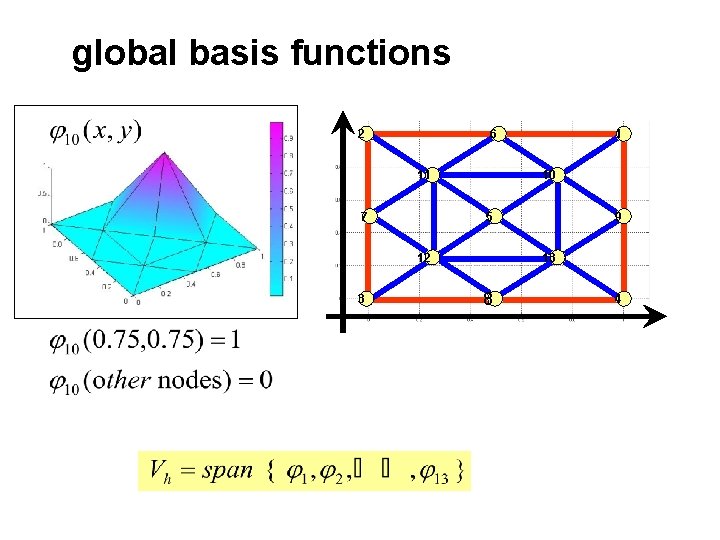
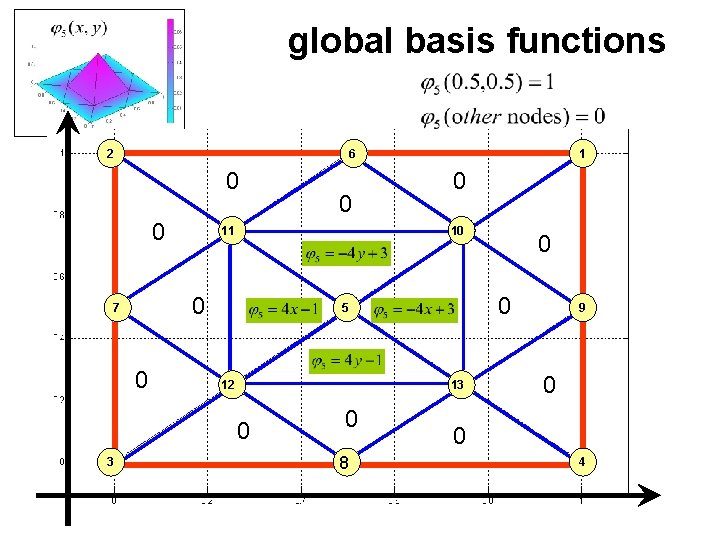
Global Basis Functions for the space of all continuous piecewise linear polynomials To construct a basis for this space we note that a function v in this space is uniquely determined by its nodal values where n is the number of nodes in the mesh

Example (for global basis functions)

global basis functions 2 6 11 7 10 5 12 3 1 9 13 8 4

global basis functions 2 6 11 7 10 5 12 3 1 9 13 8 4

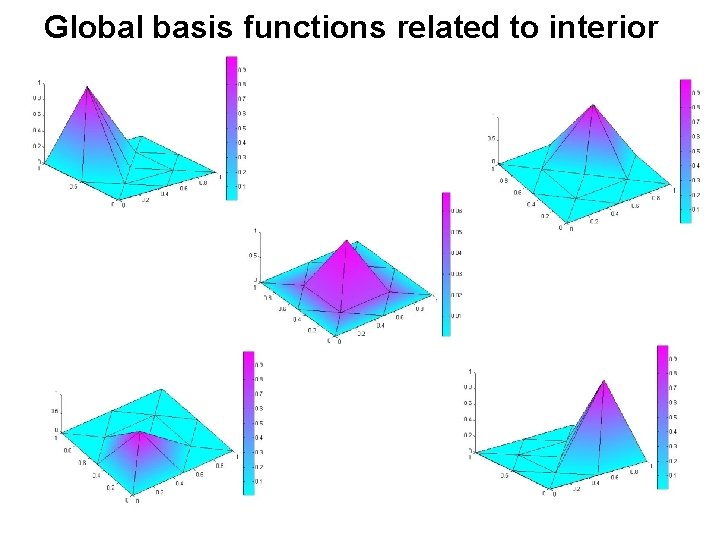
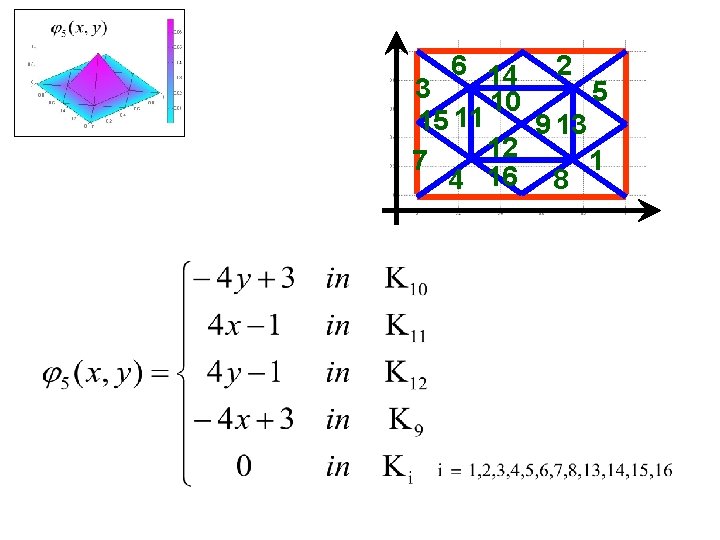
Global basis functions related to interior nodes

global basis functions 2 6 0 0 11 0 12 13 0 8 0 0 5 0 3 0 10 0 7 0 1 9 0 0 4

6 14 2 3 5 10 15 11 9 13 12 7 1 4 16 8

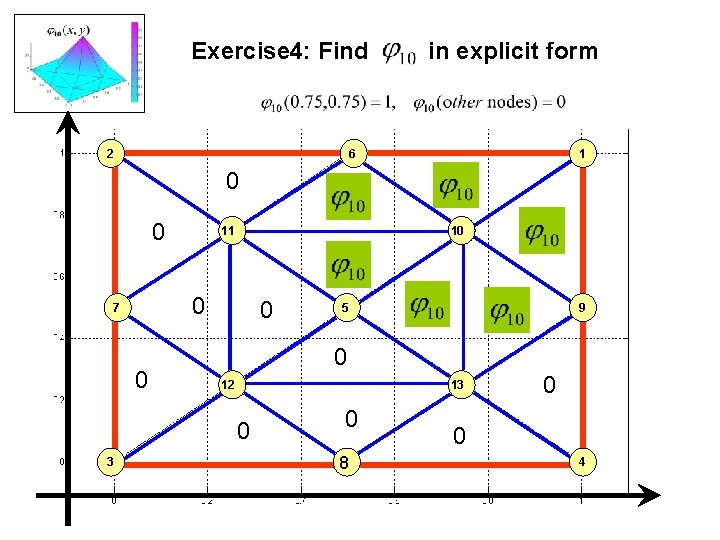
Exercise 4: Find 2 in explicit form 6 1 0 0 11 10 0 7 0 0 9 0 12 13 0 3 5 0 8 0 0 4

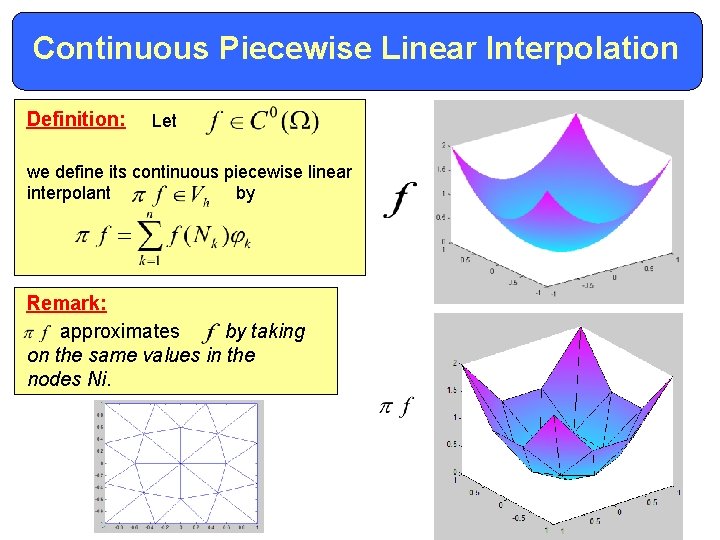
Continuous Piecewise Linear Interpolation Definition: Let we define its continuous piecewise linear interpolant by Remark: approximates by taking on the same values in the nodes Ni.

to draw πf given f [p, e, t] = initmesh('squareg', 'hmax', 0. 7); % mesh x = p(1, : ); y = p(2, : ); % node coordinates pif = x. ^2+ y. ^2; % nodal values of interpolant pdesurf(p, t, pif') % plot interpolant %pdeplot(p, e, t, 'xydata', pif, 'zdata', pif, 'mesh', 'on');

Piecewise Polynomial Spaces Definition: triangle with nodes be the space of linear functions on Remark: We observe that any function in. P 1(K) is uniquely determined by its nodal values Reference triangle