PID Tuning and Controllability Sigurd Skogestad NTNU Trondheim

PID Tuning and Controllability Sigurd Skogestad NTNU, Trondheim, Norway April 4 -8, 2004 KFUPM-Distillation Control Course

Tuning of PID controllers n n n SIMC tuning rules (“Skogestad IMC”)(*) Main message: Can usually do much better by taking a systematic approach One tuning rule! Easily memorized • • k’ = k/τ1 = initial slope step response c ≥ 0: desired closed-loop response time (tuning parameter) For robustness select (1) : c ¸ (gives Kc ≤ Kc, max) For acceptable disturbance rejection select (2) : Kc ≥ Kc, min = ud 0/ymax References: (1) S. Skogestad, “Simple analytic rules for model reduction and PID controller design”, J. Proc. Control, Vol. 13, 291 -309, 2003 (2) S. Skogestad, ``Tuning for smooth PID control with acceptable disturbance rejection'', Ind. Eng. Chem. Res, 45 (23), 7817 -7822 (2006). (*) “Probably the best simple PID tuning rules in the world” April 4 -8, 2004 KFUPM-Distillation Control Course 2

Need a model for tuning n Model: Dynamic effect of change in input u (MV) on output y (CV) First-order + delay model for PI-control n Second-order model for PID-control n April 4 -8, 2004 KFUPM-Distillation Control Course 3

Step response experiment n n Make step change in one u (MV) at a time Record the output (s) y (CV) April 4 -8, 2004 KFUPM-Distillation Control Course 4
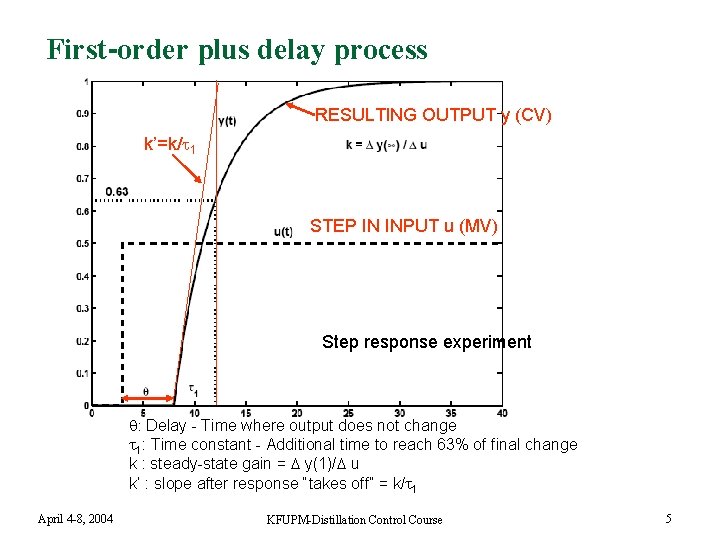
First-order plus delay process RESULTING OUTPUT y (CV) k’=k/ 1 STEP IN INPUT u (MV) Step response experiment : Delay - Time where output does not change 1: Time constant - Additional time to reach 63% of final change k : steady-state gain = y(1)/ u k’ : slope after response “takes off” = k/ 1 April 4 -8, 2004 KFUPM-Distillation Control Course 5

Model reduction of more complicated model n Start with complicated stable model on the form n Want to get a simplified model on the form n Most important parameter is usually the “effective” delay April 4 -8, 2004 KFUPM-Distillation Control Course 6

April 4 -8, 2004 KFUPM-Distillation Control Course 7

April 4 -8, 2004 KFUPM-Distillation Control Course 8

half rule April 4 -8, 2004 KFUPM-Distillation Control Course 9

Approximation of zeros April 4 -8, 2004 KFUPM-Distillation Control Course 10

Derivation of SIMC-PID tuning rules n PI-controller (based on first-order model) n For second-order model add D-action. For our purposes it becomes simplest with the “series” (cascade) PID-form: April 4 -8, 2004 KFUPM-Distillation Control Course 11
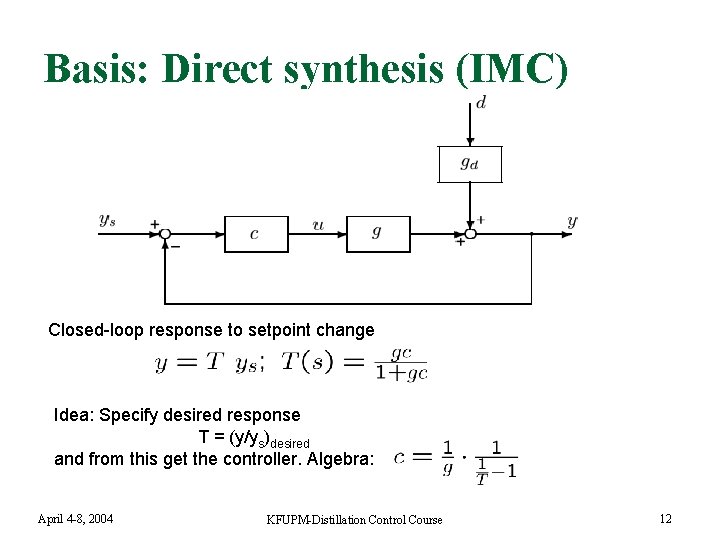
Basis: Direct synthesis (IMC) Closed-loop response to setpoint change Idea: Specify desired response T = (y/ys)desired and from this get the controller. Algebra: April 4 -8, 2004 KFUPM-Distillation Control Course 12

IMC Tuning = Direct Synthesis April 4 -8, 2004 KFUPM-Distillation Control Course 13

Integral time n n n Found: Integral time = dominant time constant ( I = 1) Works well for setpoint changes Needs to be modified (reduced) for integrating disturbances d c u g y Example. “Almost-integrating process” with disturbance at input: G(s) = e-s/(30 s+1) Original integral time I = 30 gives poor disturbance response Try reducing it! April 4 -8, 2004 KFUPM-Distillation Control Course 14
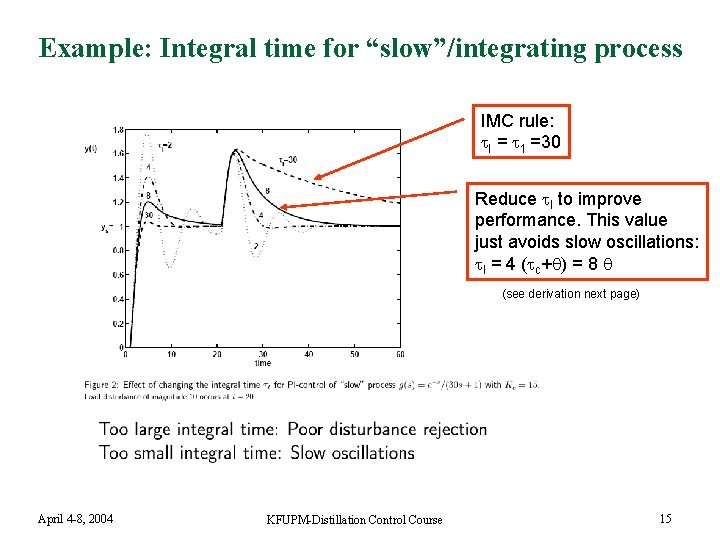
Example: Integral time for “slow”/integrating process IMC rule: I = 1 =30 Reduce I to improve performance. This value just avoids slow oscillations: I = 4 ( c+ ) = 8 (see derivation next page) April 4 -8, 2004 KFUPM-Distillation Control Course 15

Derivation integral time: Avoiding slow oscillations for integrating process. n n Integrating process: 1 large Assume 1 large and neglect delay : n n n PI-control: C(s) = Kc (1 + 1/ I s) Poles (and oscillations) are given by roots of closed-loop polynomial n n 1+GC = 1 + k’/s ¢ Kc ¢ (1+1/ Is) = 0 or I s 2 + k’ Kc I s + k’ Kc = 0 Can be written on standard form ( 02 s 2 + 2 0 s + 1) with To avoid oscillations must require | |¸ 1: n n n G(s) = k e- s /( 1 s + 1) ¼ k/( 1 s) = k’/s Kc ¢ k’ ¢ I ¸ 4 or I ¸ 4 / (Kc k’) With choice Kc = (1/k’) (1/( c+ )) this gives I ¸ 4 ( c+ ) Conclusion integrating process: Want I small to improve performance, but must be larger than 4 ( c+ ) to avoid slow oscillations April 4 -8, 2004 KFUPM-Distillation Control Course 16

Summary: SIMC-PID Tuning Rules One tuning parameter: c April 4 -8, 2004 KFUPM-Distillation Control Course 17

Some special cases One tuning parameter: c April 4 -8, 2004 KFUPM-Distillation Control Course 18
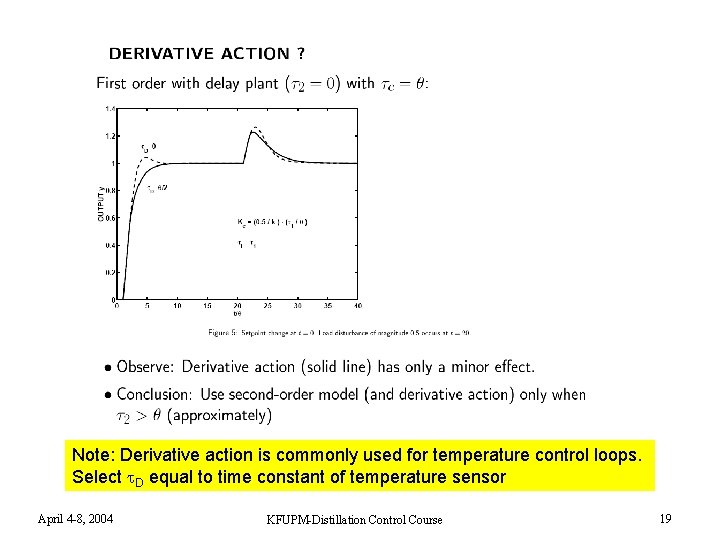
Note: Derivative action is commonly used for temperature control loops. Select D equal to time constant of temperature sensor April 4 -8, 2004 KFUPM-Distillation Control Course 19

April 4 -8, 2004 KFUPM-Distillation Control Course 20

Selection of tuning parameter c Two cases 1. Tight control: Want “fastest possible control” subject to having good robustness • 2. (1) S. Skogestad, “Simple analytic rules for model reduction and PID controller design”, J. Proc. Control, Vol. 13, 291309, 2003 Smooth control: Want “slowest possible control” subject to having acceptable disturbance rejection • April 4 -8, 2004 (2) S. Skogestad, ``Tuning for smooth PID control with acceptable disturbance rejection'', Ind. Eng. Chem. Res, 45 (23), 7817 -7822 (2006). KFUPM-Distillation Control Course 21

(1) TIGHT CONTROL April 4 -8, 2004 KFUPM-Distillation Control Course 22
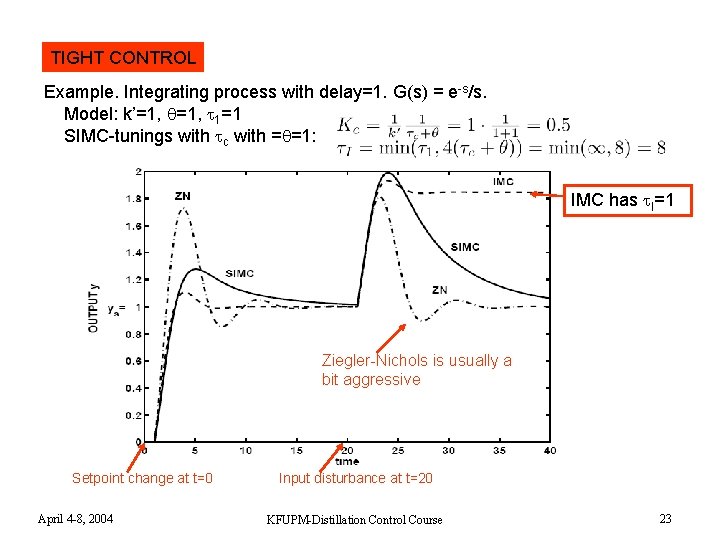
TIGHT CONTROL Example. Integrating process with delay=1. G(s) = e-s/s. Model: k’=1, 1=1 SIMC-tunings with c with = =1: IMC has I=1 Ziegler-Nichols is usually a bit aggressive Setpoint change at t=0 April 4 -8, 2004 Input disturbance at t=20 KFUPM-Distillation Control Course 23
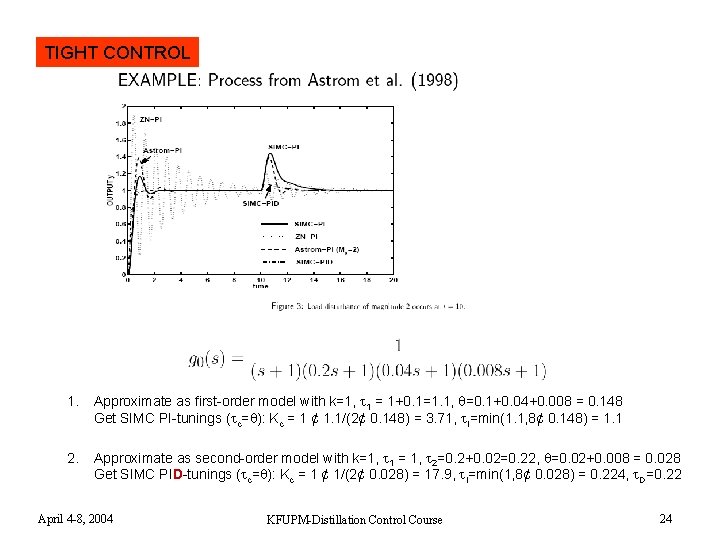
TIGHT CONTROL 1. Approximate as first-order model with k=1, 1 = 1+0. 1=1. 1, =0. 1+0. 04+0. 008 = 0. 148 Get SIMC PI-tunings ( c= ): Kc = 1 ¢ 1. 1/(2¢ 0. 148) = 3. 71, I=min(1. 1, 8¢ 0. 148) = 1. 1 2. Approximate as second-order model with k=1, 1 = 1, 2=0. 2+0. 02=0. 22, =0. 02+0. 008 = 0. 028 Get SIMC PID-tunings ( c= ): Kc = 1 ¢ 1/(2¢ 0. 028) = 17. 9, I=min(1, 8¢ 0. 028) = 0. 224, D=0. 22 April 4 -8, 2004 KFUPM-Distillation Control Course 24

(2) SMOOTH CONTROL Tuning for smooth control n Tuning parameter: c = desired closed-loop response time n (1) Selecting c= (“tight control”) is reasonable for cases with a relatively large effective delay n Other cases: Select c > for q q slower control smoother input usage n q q n less disturbing effect on rest of the plant less sensitivity to measurement noise better robustness Question: Given that we require some disturbance rejection. q q What is the largest possible value for c ? Or equivalently: The smallest possible value for Kc? (2) Will derive Kc, min. From this we can get c, max using SIMC tuning rule April 4 -8, 2004 KFUPM-Distillation Control Course 25
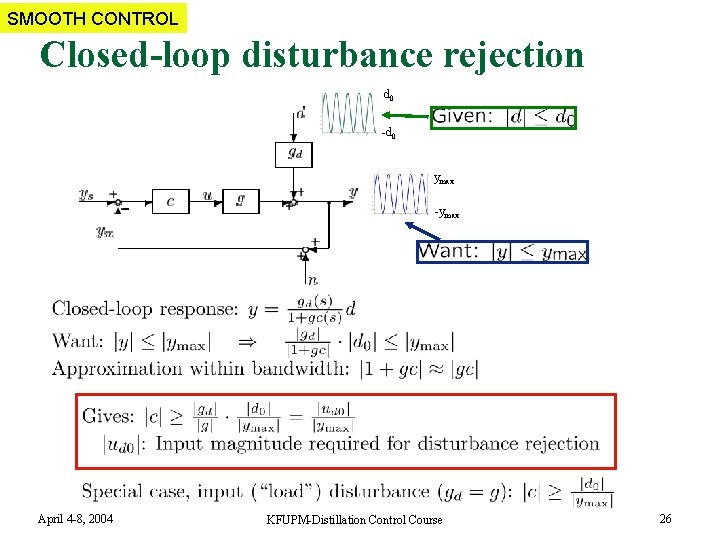
SMOOTH CONTROL Closed-loop disturbance rejection d 0 -d 0 ymax -ymax April 4 -8, 2004 KFUPM-Distillation Control Course 26
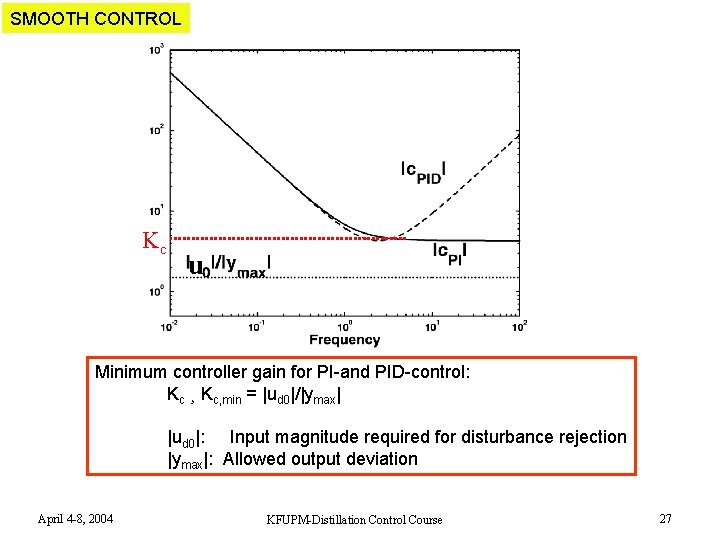
SMOOTH CONTROL Kc u Minimum controller gain for PI-and PID-control: Kc ¸ Kc, min = |ud 0|/|ymax| |ud 0|: Input magnitude required for disturbance rejection |ymax|: Allowed output deviation April 4 -8, 2004 KFUPM-Distillation Control Course 27

SMOOTH CONTROL Minimum controller gain: Industrial practice: Variables (instrument ranges) often scaled such that (span) Minimum controller gain is then Minimum gain for smooth control ) Common default factory setting Kc=1 is reasonable ! April 4 -8, 2004 KFUPM-Distillation Control Course 28
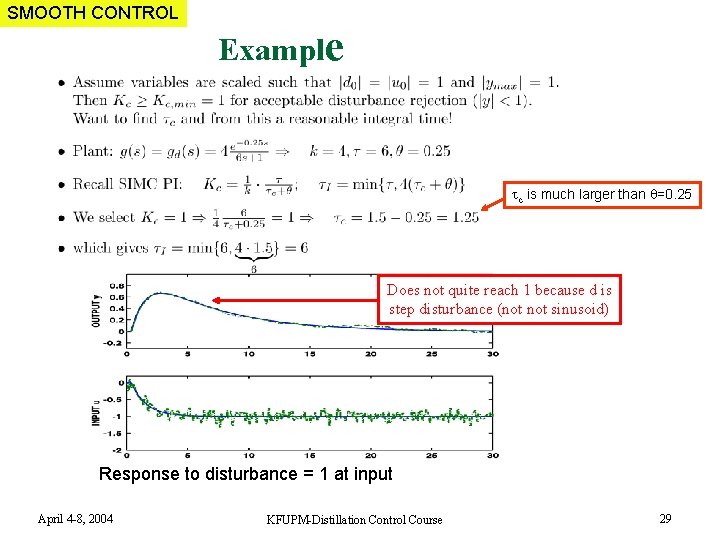
SMOOTH CONTROL Example c is much larger than =0. 25 Does not quite reach 1 because d is step disturbance (not sinusoid) Response to disturbance = 1 at input April 4 -8, 2004 KFUPM-Distillation Control Course 29

SMOOTH CONTROL LEVEL CONTROL Application of smooth control n Averaging level control q V LC If you insist on integral action then this value avoids cycling Reason for having tank is to smoothen disturbances in concentration and flow. Tight level control is not desired: gives no “smoothening” of flow disturbances. Derivation of tunings: Minimum controller gain for acceptable disturbance rejection: Kc ¸≥ Kc, min = |ud 0|/|ymax| Where in our case |ud 0| = | q 0| - expected flow change [m 3/s] (input disturbance) |ymax| = | Vmax| - largest allowed variation in level [m 3] Integral time: From the material balance (d. V/dt = q – qout), the model is g(s)=k’/s with k’=1. Select Kc=Kc, min = | q 0| | Vmax|. SIMC-Integral time for integrating process: I = 4 / (k’ Kc) = 4 | Vmax| / | q 0| = 4 ¢ residence time provided tank is nominally half full (so | Vmax| = V) and q 0 is equal to the nominal flow. April 4 -8, 2004 KFUPM-Distillation Control Course 30

SMOOTH CONTROL Rule: Kc ¸ |ud 0|/|ymax| ( ~1 in scaled variables) n Exception to rule: Can have even smaller Kc (< 1) if disturbances are handled by the integral action. q q q Happens when c > I = 1 Applies to: Process with short time constant ( 1 is small) For example, flow control Kc: Assume variables are scaled with respect to their span April 4 -8, 2004 KFUPM-Distillation Control Course 31

SMOOTH CONTROL Summary: Tuning of easy loops n n Easy loops: Small effective delay ( ¼ 0), so closedloop response time c (>> ) is selected for “smooth control” Flow control: Kc=0. 5, I = 1 = time constant valve (typically, 10 s to 30 s) Level control: Kc=2 (and no integral action) Other easy loops (e. g. pressure control): Kc = 2, I = min(4 c, 1) q Note: Often want a tight pressure control loop (so may have Kc=10 or larger) Kc: Assume variables are scaled with respect to their span April 4 -8, 2004 KFUPM-Distillation Control Course 32

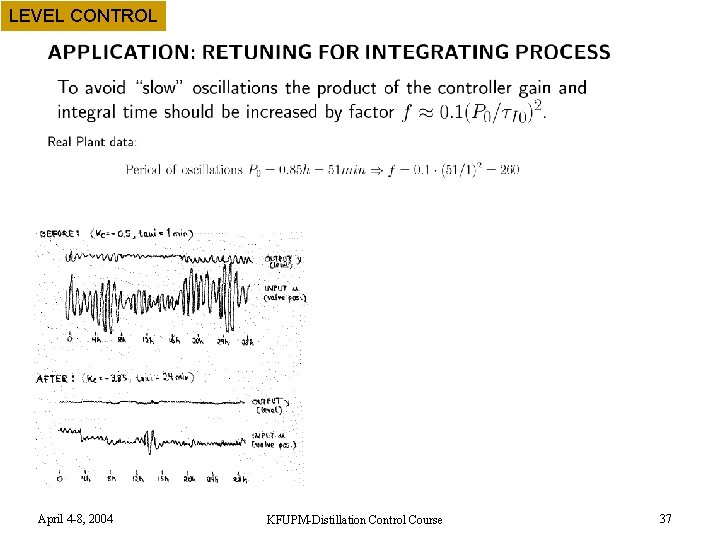
LEVEL CONTROL More on level control n n Level control often causes problems Typical story: q q n n Level loop starts oscillating Operator detunes by decreasing controller gain Level loop oscillates even more. . . ? ? ? Explanation: Level is by itself unstable and requires control. April 4 -8, 2004 KFUPM-Distillation Control Course 33

LEVEL CONTROL Integrating process : Level control April 4 -8, 2004 KFUPM-Distillation Control Course 34

LEVEL CONTROL How avoid oscillating levels? Actually, 0. 1 = 1/π2 April 4 -8, 2004 KFUPM-Distillation Control Course 35

LEVEL CONTROL Case study oscillating level n n n We were called upon to solve a problem with oscillations in a distillation column Closer analysis: Problem was oscillating reboiler level in upstream column Use of Sigurd’s rule solved the problem April 4 -8, 2004 KFUPM-Distillation Control Course 36
LEVEL CONTROL April 4 -8, 2004 KFUPM-Distillation Control Course 37

Identifying the model April 4 -8, 2004 KFUPM-Distillation Control Course 38

Model identification from step response n n General: Need 3 parameters: q Delay q 2 of the following: k, k’, 1 (Note relationship k’ = k/ 1) Two approaches for obtaining 1: 1. 2. q Initial response: ( + 1) is where initial slope crosses final steady-state ( + 1)= 63% of final steady state If disagree: Initial response is usually best, but to be safe use smallest value for 1 (“fast response”) as this gives more conservative PID-tunings April 4 -8, 2004 n 1 = 16 min for this case k’ BOTTOM V: -0. 5 k 63% x. B 1=16 min / 19 min KFUPM-Distillation Control Course 39
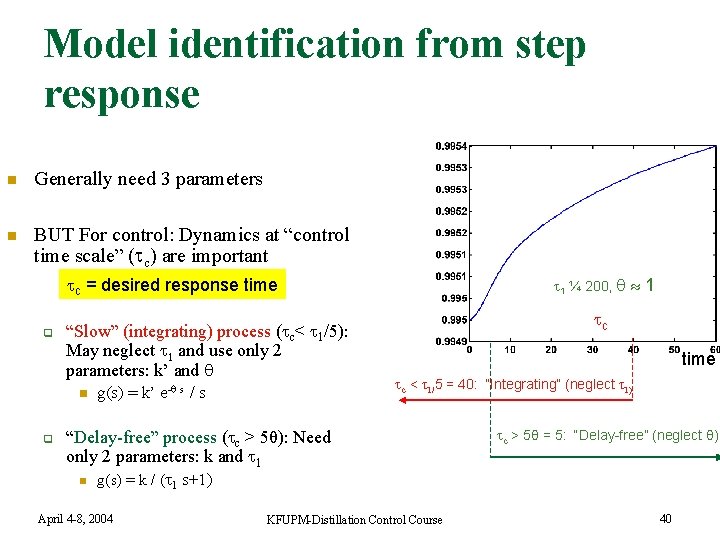
Model identification from step response n Generally need 3 parameters n BUT For control: Dynamics at “control time scale” ( c) are important c = desired response time q “Slow” (integrating) process ( c< 1/5): May neglect 1 and use only 2 parameters: k’ and n q g(s) = k’ e- s / s 1 ¼ 200, c time c < τ1/5 = 40: “Integrating” (neglect τ1) “Delay-free” process ( c > 5θ): Need only 2 parameters: k and 1 n 1 c > 5θ = 5: “Delay-free” (neglect θ) g(s) = k / ( 1 s+1) April 4 -8, 2004 KFUPM-Distillation Control Course 40
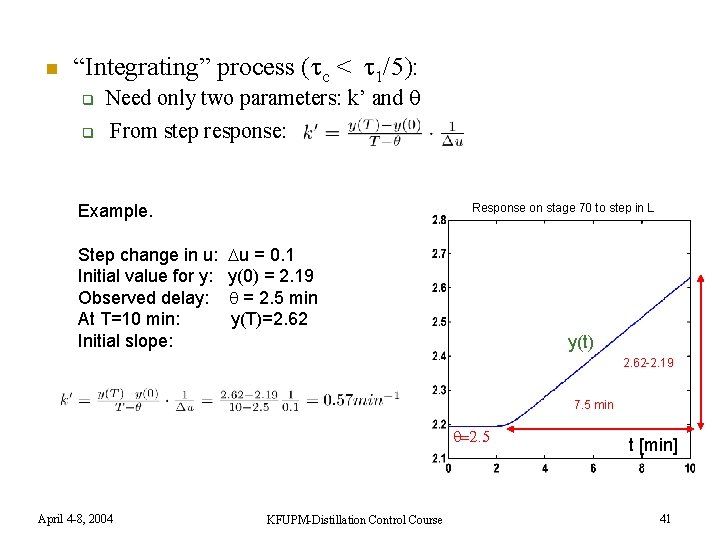
n “Integrating” process ( c < 1/5): q q Need only two parameters: k’ and From step response: Response on stage 70 to step in L Example. Step change in u: Initial value for y: Observed delay: At T=10 min: Initial slope: u = 0. 1 y(0) = 2. 19 = 2. 5 min y(T)=2. 62 y(t) 2. 62 -2. 19 7. 5 min =2. 5 April 4 -8, 2004 KFUPM-Distillation Control Course t [min] 41
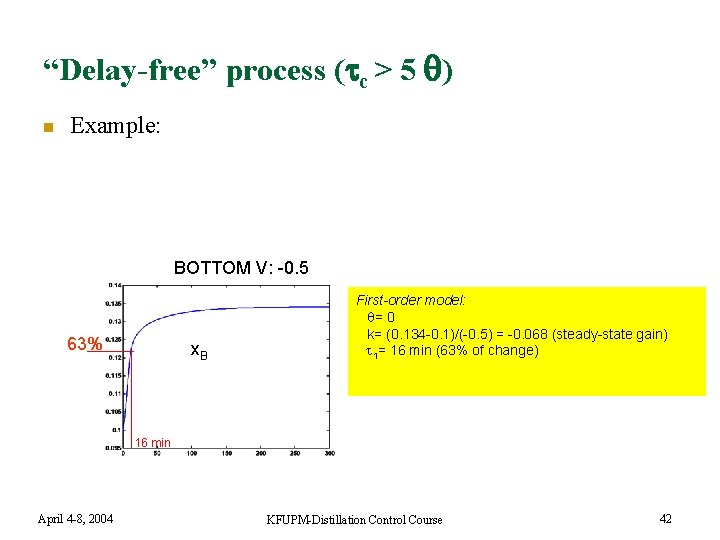
“Delay-free” process ( c > 5 ) n Example: BOTTOM V: -0. 5 63% x. B First-order model: = 0 k= (0. 134 -0. 1)/(-0. 5) = -0. 068 (steady-state gain) 1= 16 min (63% of change) 16 min April 4 -8, 2004 KFUPM-Distillation Control Course 42

Step response experiment: How long do we need to wait? q NORMALLY NO NEED TO RUN THE STEP EXPERIMENT FOR LONGER THAN ABOUT 10 TIMES THE EFFECTIVE DELAY ( ) April 4 -8, 2004 KFUPM-Distillation Control Course 43

Conclusion PID tuning April 4 -8, 2004 KFUPM-Distillation Control Course 44

April 4 -8, 2004 KFUPM-Distillation Control Course 45
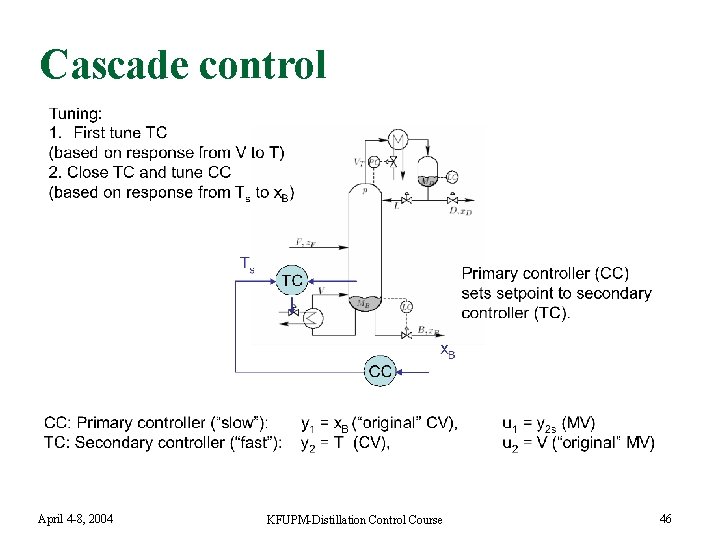
Cascade control April 4 -8, 2004 KFUPM-Distillation Control Course 46

Tuning of cascade controllers April 4 -8, 2004 KFUPM-Distillation Control Course 47
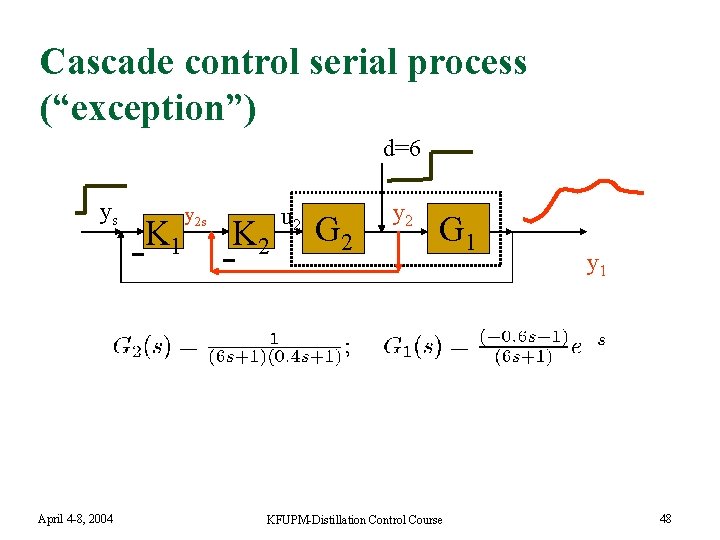
Cascade control serial process (“exception”) d=6 ys April 4 -8, 2004 K 1 y 2 s K 2 u 2 G 2 y 2 G 1 KFUPM-Distillation Control Course y 1 48
Cascade control serial process d=6 ys K 1 y 2 s K 2 u G 2 y 2 G 1 y 1 Without cascade With cascade April 4 -8, 2004 KFUPM-Distillation Control Course 49

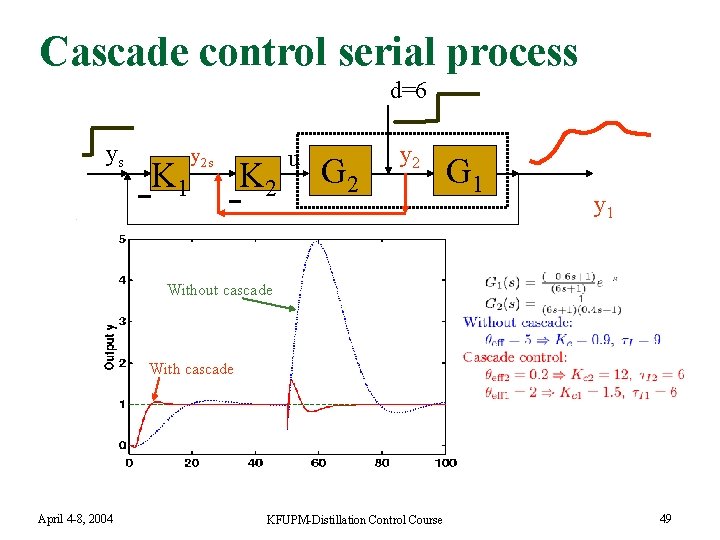
Tuning cascade control : serial process n Inner fast (secondary) loop: q q q n Outer slower primary loop: q n Reduced effective delay (2 s instead of 6 s) Time scale separation q n P or PI-control Local disturbance rejection Much smaller effective delay (0. 2 s) Inner loop can be modelled as gain=1 + 2*effective delay (0. 4 s) Very effective for control of large-scale systems April 4 -8, 2004 KFUPM-Distillation Control Course 50

CONTROLLABILITY Controllability n n (Input-Output) “Controllability” is the ability to achieve acceptable control performance (with any controller) “Controllability” is a property of the process itself Analyze controllability by looking at model G(s) What limits controllability? April 4 -8, 2004 KFUPM-Distillation Control Course 51

CONTROLLABILITY Controllability Recall SIMC tuning rules 1. Tight control: Select c= corresponding to 2. Smooth control. Select Kc ¸ Must require Kc, max > Kc. min for controllability ) max. output deviation initial effect of “input” disturbance April 4 -8, 2004 KFUPM-Distillation Control Course y reaches k’ ¢ |d 0|¢ t after time t y reaches ymax after t= |ymax|/ k’ ¢ |d 0| 52

CONTROLLABILITY Controllability April 4 -8, 2004 KFUPM-Distillation Control Course 53
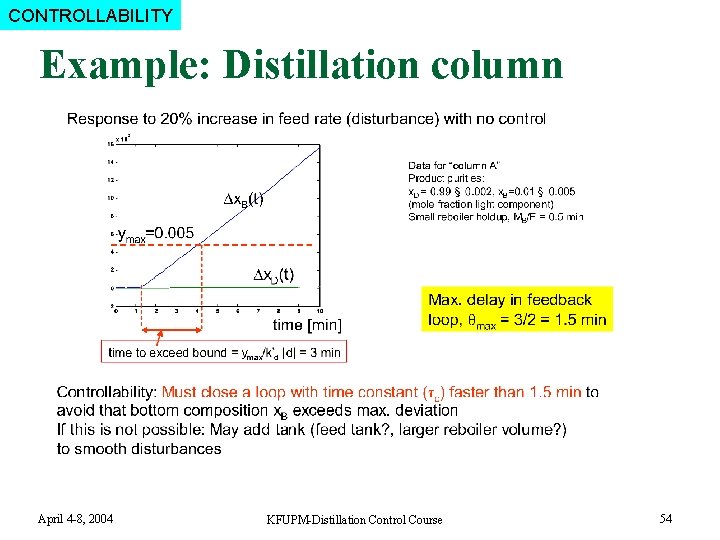
CONTROLLABILITY Example: Distillation column April 4 -8, 2004 KFUPM-Distillation Control Course 54
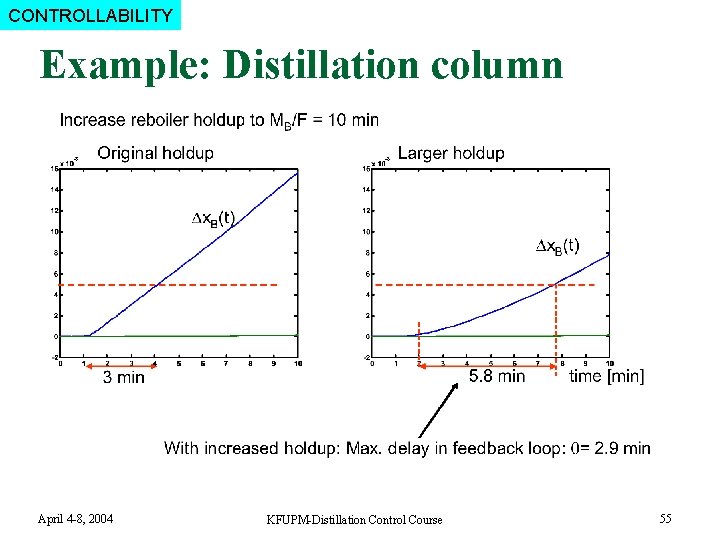
CONTROLLABILITY Example: Distillation column April 4 -8, 2004 KFUPM-Distillation Control Course 55
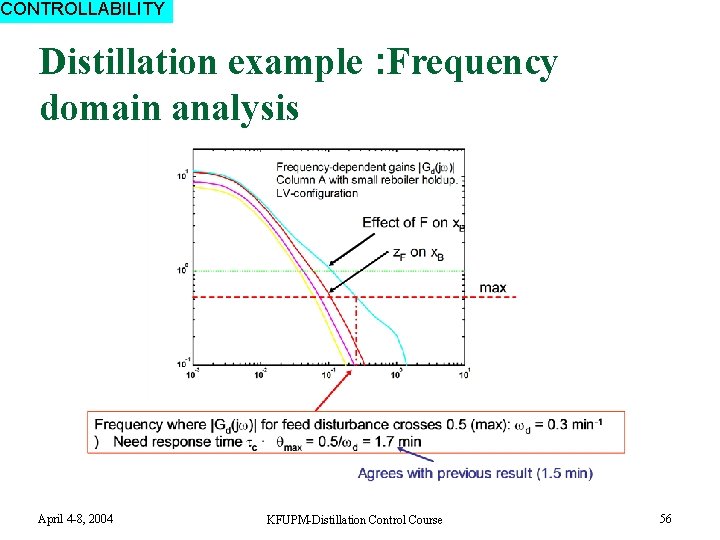
CONTROLLABILITY Distillation example : Frequency domain analysis April 4 -8, 2004 KFUPM-Distillation Control Course 56

CONTROLLABILITY Other factors limiting controllability n n Input limitations (saturation or “slow valve”): Can sometimes limit achievable speed of response Unstable process (including levels): Need feedback control for stabilization ) Makes sure inputs do not saturate in stabilizing loops April 4 -8, 2004 KFUPM-Distillation Control Course 57
- Slides: 57