PID CONTROLLER Introduction Pengendali otomatis membandingkan nilai sebenarnya

PID CONTROLLER

Introduction • • Pengendali otomatis membandingkan nilai sebenarnya dari keluaran sistem dengan masukannya, menentukan penyimpangan dan menghasilkan sinyal kendali yang akan mengurangi penyimpangan sehingga menjadi nol atau sekecil mungkin. Pengendali proportional, integral dan derivative (PID) sangat populer di industri karena sederhana dalam desainnya dan sudah teruji kehandalannya. Click to edit the outline text format Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

The three-term controller • • Transfer function dari pengendali PID adalah sebagai berikut: § Kp = Proportional gain § KI = Integral gain § Kd = Derivative gain Dari blok diagram sistem close loop diatas, sinyal error (e) akan dikirim ke PID controller, selanjutnya PID controller akan menghitung dan mengeluarkan sinyal control law (u) sebesar:

The characteristics of P, I, and D controllers • • • Proportional controller Kp berdampak: mengurangi rise time, mengurangi tapi tidak bisa menghilangkan steady state error. Integral controller Ki berdampak: menghilangkan steady state error namun membuat transient respon-nya jelek. Derivative controller Kd berdampak: meningkatkan stabilitas sistem, mengurangi overshoot dan memperbaiki transient response.

Example Problem • Persamaan differensial sistem disamping adalah: Click to edit the outline text format • • • Dengan transformasi Laplace didapat: Transfer function dari sistem ini adlah: Misalnya diambil data: – M = 1 kg Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

• Memasukkan data diatas kedalam transfer function diperoleh: • Kita akan memdesain PID controller dengan design criteria sbb: – Fast rise time – Minimum overshoot – No steady-state error

Open-loop step response • Matlab program: num=1; den=[1 10 20]; plant=tf(num, den); step(plant) • – steady-state error of 0. 95 – rise time is about one second – and the settling time is about 1. 5 seconds. Let's design a controller that will reduce the rise time, reduce the Click to edit the outline text format Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

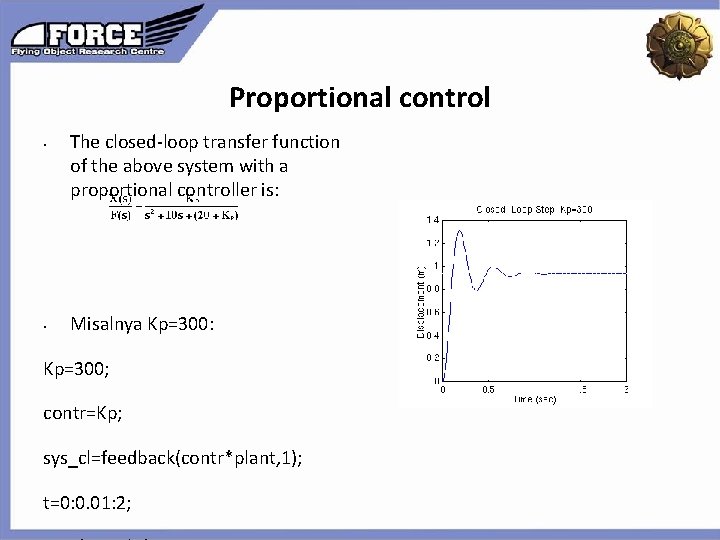
Proportional control • The closed-loop transfer function of the above system with a proportional controller is: Click to edit the outline text format Second Outline Level • Misalnya Kp=300: Kp=300; contr=Kp; sys_cl=feedback(contr*plant, 1); t=0: 0. 01: 2; Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

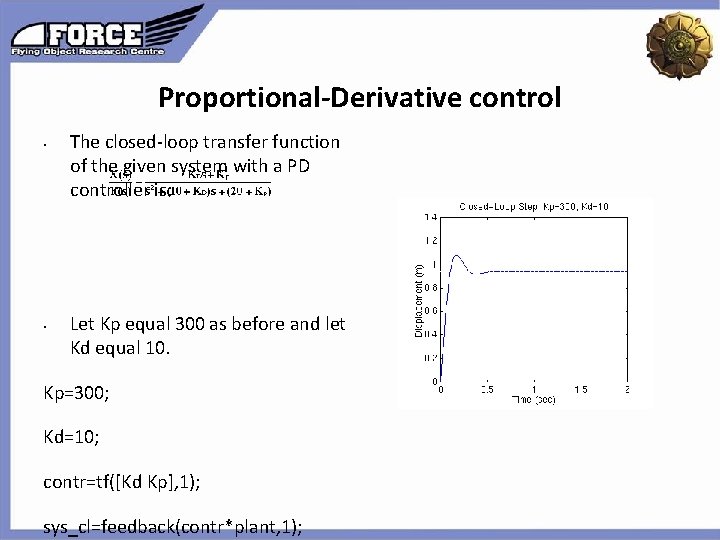
Proportional-Derivative control • The closed-loop transfer function of the given system with a PD controller is: Click to edit the outline text format Second Outline Level • Let Kp equal 300 as before and let Kd equal 10. Kp=300; Kd=10; contr=tf([Kd Kp], 1); sys_cl=feedback(contr*plant, 1); Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

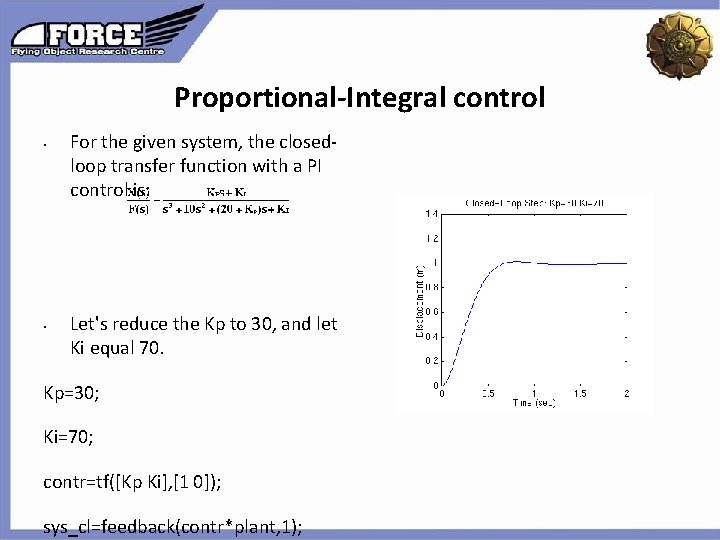
Proportional-Integral control • For the given system, the closedloop transfer function with a PI control is: Click to edit the outline text format Second Outline Level • Let's reduce the Kp to 30, and let Ki equal 70. Kp=30; Ki=70; contr=tf([Kp Ki], [1 0]); sys_cl=feedback(contr*plant, 1); Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

Proportional-Integral-Derivative control • The closed-loop transfer function of the given system with a PID controller is: Click to edit the outline text format Second Outline Level • After several trial and error runs, the gains Kp=350, Ki=300, and Kd=50 provided the desired response. Kp=350; Ki=300; Kd=50; Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

General tips for designing a PID controller 1. Obtain an open-loop response and determine what needs to be improved 2. Add a proportional control to improve the rise time 3. Add a derivative control to improve the overshoot 4. Add an integral control to eliminate the steady-state error 5. Adjust each of Kp, Ki, and Kd until you obtain a desired overall response. You can always refer to the table shown in this "PID Tutorial" page to find out which controller controls what characteristics.

• Example: PID Design method for the Pitch EOM of an aircraft can be Controller Click to edit the outline decoupled and linearized into the longitudinal and lateral equations. Pitch control is a longitudinal problem, and in this example, we will design an autopilot that controls the pitch of an aircraft. • The longitudinal equations of motion of an aircraft can be written as: text format Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

Transfer function model • • Let's plug in some numerical values to simplify the modeling equations (1) shown above. These values are taken from the data from one of Boeing's commercial aircraft. The Laplace transform of the above equations are shown below. After few steps of algebra, you should obtain the following transfer function.

Design requirements § Overshoot: Less than 10% § Rise time: Less than 2 seconds § Settling time: Less than 10 seconds § Steady-state error: Less than 2%

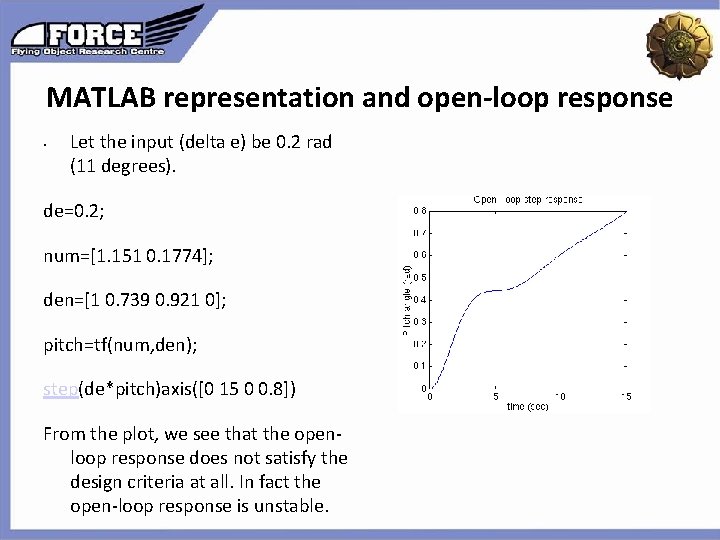
MATLAB representation and open-loop response • Let the input (delta e) be 0. 2 rad (11 degrees). de=0. 2; num=[1. 151 0. 1774]; Click to edit the outline text format Second Outline Level den=[1 0. 739 0. 921 0]; pitch=tf(num, den); step(de*pitch)axis([0 15 0 0. 8]) From the plot, we see that the openloop response does not satisfy the design criteria at all. In fact the open-loop response is unstable. Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

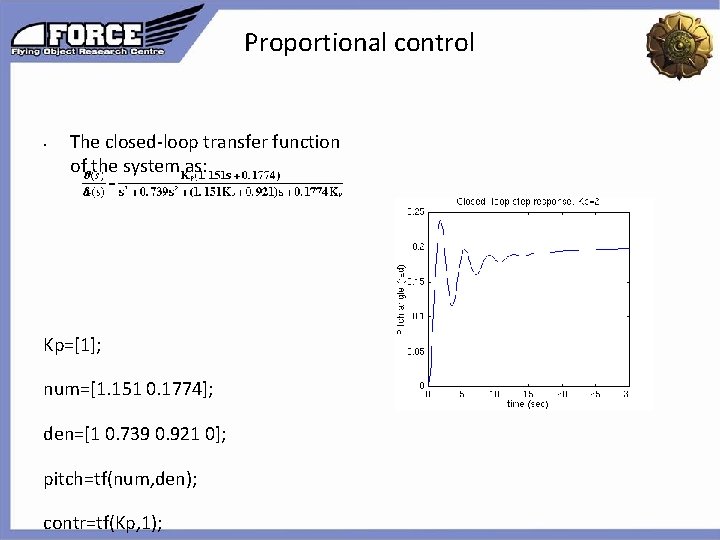
Proportional control • The closed-loop transfer function of the system as: Click to edit the outline text format Second Outline Level Kp=[1]; num=[1. 151 0. 1774]; den=[1 0. 739 0. 921 0]; pitch=tf(num, den); contr=tf(Kp, 1); Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

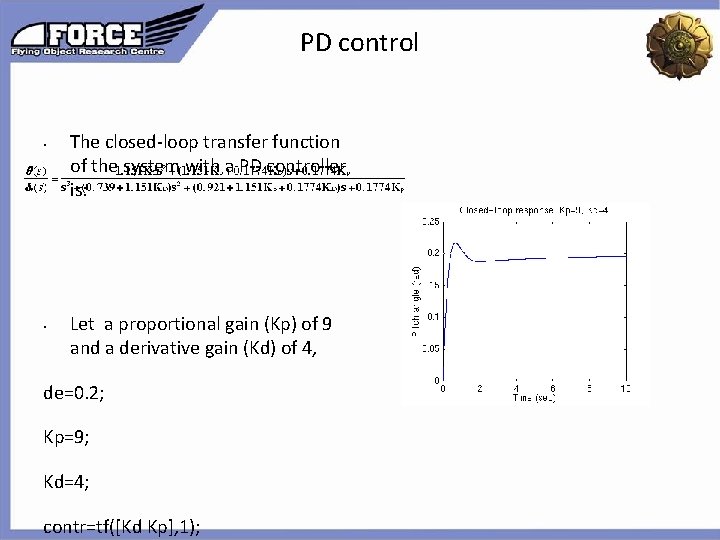
PD control • The closed-loop transfer function of the system with a PD controller is: Click to edit the outline text format Second Outline Level • Let a proportional gain (Kp) of 9 and a derivative gain (Kd) of 4, de=0. 2; Kp=9; Kd=4; contr=tf([Kd Kp], 1); Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

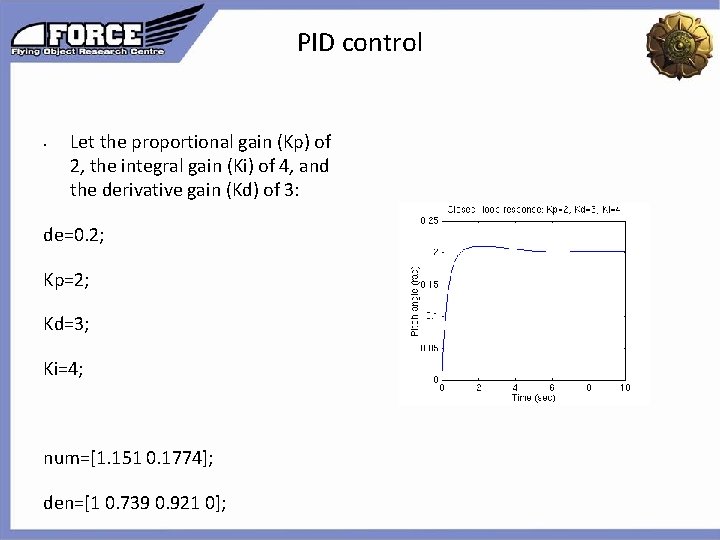
PID control • Let the proportional gain (Kp) of 2, the integral gain (Ki) of 4, and the derivative gain (Kd) of 3: de=0. 2; Kp=2; Kd=3; Ki=4; num=[1. 151 0. 1774]; den=[1 0. 739 0. 921 0]; Click to edit the outline text format Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth