Picosecond time measurement using ultra fast analog memories

Picosecond time measurement using ultra fast analog memories: new results since SLAC workshop. D. Breton & J. Maalmi (LAL Orsay), E. Delagnes (CEA/IRFU), J. Va’Vra (SLAC) D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

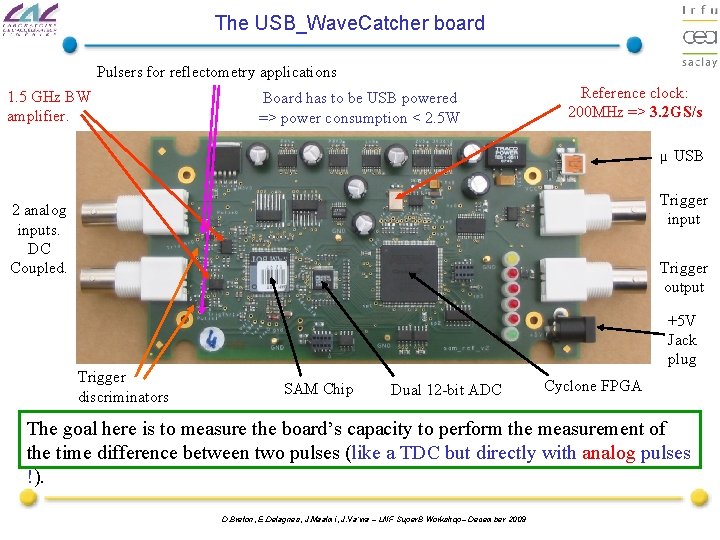
The USB_Wave. Catcher board Pulsers for reflectometry applications 1. 5 GHz BW amplifier. Board has to be USB powered => power consumption < 2. 5 W Reference clock: 200 MHz => 3. 2 GS/s µ USB Trigger input 2 analog inputs. DC Coupled. Trigger output +5 V Jack plug Trigger discriminators SAM Chip Dual 12 -bit ADC Cyclone FPGA The goal here is to measure the board’s capacity to perform the measurement of the time difference between two pulses (like a TDC but directly with analog pulses !). D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

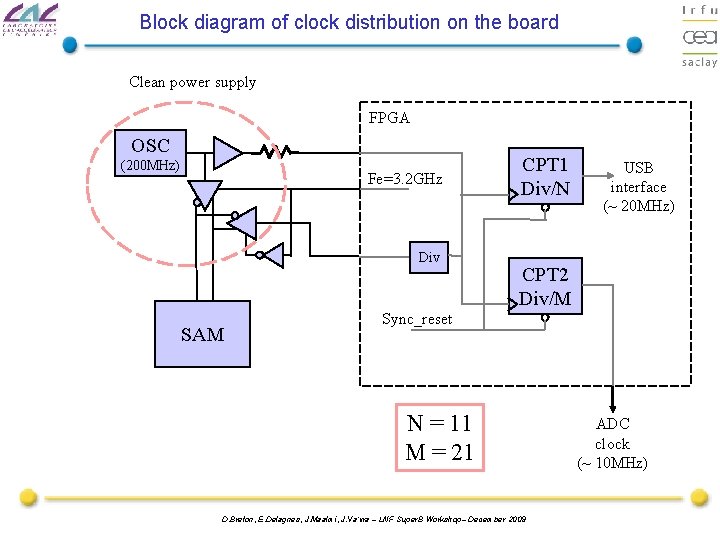
Block diagram of clock distribution on the board Clean power supply FPGA OSC (200 MHz) Fe=3. 2 GHz Div SAM CPT 1 Div/N USB interface (~ 20 MHz) CPT 2 Div/M Sync_reset N = 11 M = 21 D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009 ADC clock (~ 10 MHz)

Definition: Fixed Pattern Aperture Jitter Mismatches of elements in the delay chain induce: => dispersion of delay duration => error on the sampling time. Fixed for a given tap => “Fixed Pattern Aperture Jitter” • Dispersion of single delays => time DNL. • Cumulative effect => time INL. Gets worse with delay line length. • Systematic effect => non equidistant samples (bad for FFT). => correction with Lagrange polynomial interpolation. Drawbacks: computing power. => good (and easy) calibration required. Δt[cell] Real signal Fake signal After interpolation D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

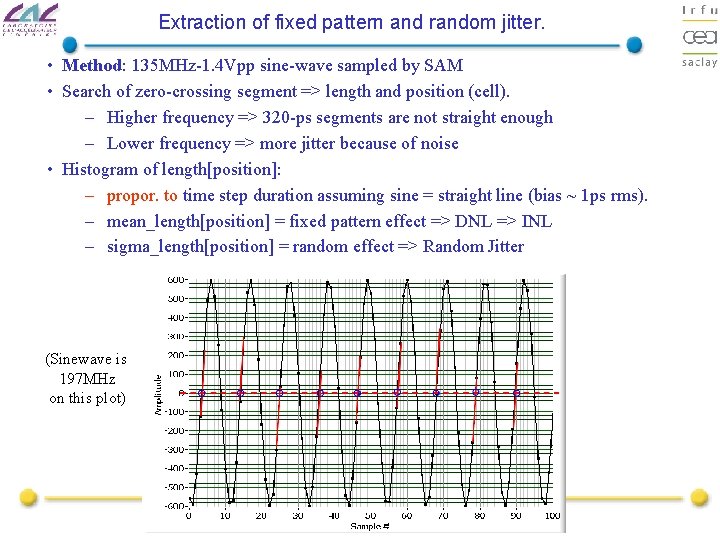
Extraction of fixed pattern and random jitter. • Method: 135 MHz-1. 4 Vpp sine-wave sampled by SAM • Search of zero-crossing segment => length and position (cell). – Higher frequency => 320 -ps segments are not straight enough – Lower frequency => more jitter because of noise • Histogram of length[position]: – propor. to time step duration assuming sine = straight line (bias ~ 1 ps rms). – mean_length[position] = fixed pattern effect => DNL => INL – sigma_length[position] = random effect => Random Jitter (Sinewave is 197 MHz on this plot) D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

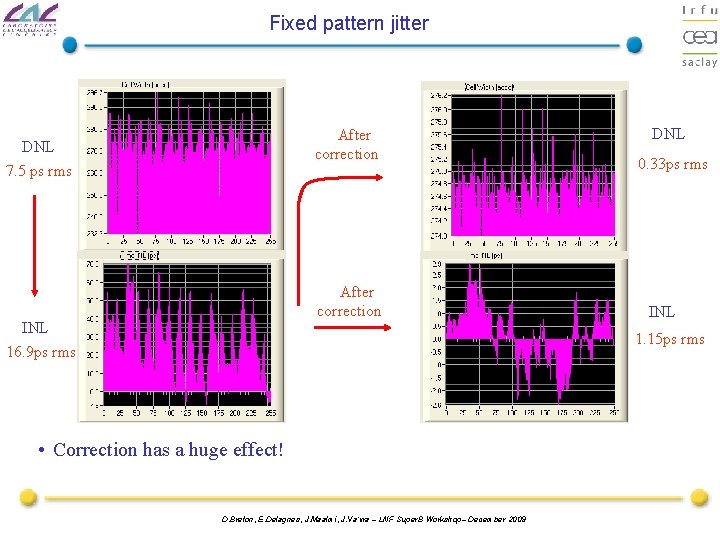
Fixed pattern jitter After correction DNL 7. 5 ps rms After correction INL 16. 9 ps rms DNL 0. 33 ps rms INL 1. 15 ps rms • Correction has a huge effect! D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

Random jitter Clock jitter 1. 95 ps rms DLL jitter • The results are very reproducible from run to run • The INL correction seems to be stable over a long period of time (days at least) Þ can be stored in the on-board EEPROM like the cell pedestals • The correction works rather well for other input frequencies between 100 and 200 MHz, with a residual INL always remaining below 2. 5 ps. => this validates the correction method. D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

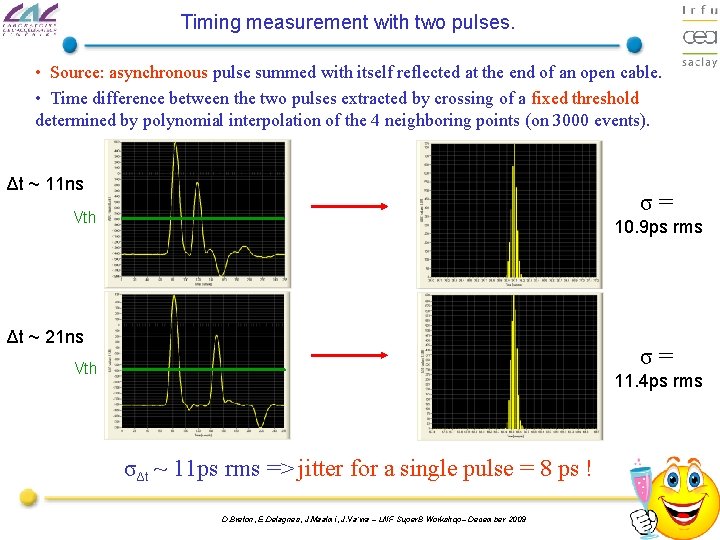
Timing measurement with two pulses. • Source: asynchronous pulse summed with itself reflected at the end of an open cable. • Time difference between the two pulses extracted by crossing of a fixed threshold determined by polynomial interpolation of the 4 neighboring points (on 3000 events). Δt ~ 11 ns σ= Vth 10. 9 ps rms Δt ~ 21 ns σ= Vth 11. 4 ps rms σΔt ~ 11 ps rms => jitter for a single pulse = 8 ps ! D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

Remarks about effects of time non-linearity. • Effects of time DNL and INL on time measurements might be misunderstood. • When measuring the time difference between two close pulses with a an analog memory, these effects really depend on the memory structure. • For instance, if one sends asynchronous pulses with a constant and short delay (a few ns), the jitter will be mainly due to the variations in the local DNL along the few consecutive cells involved in each measurement. But the effect of the local INL will be mostly masked. This means: – That jitter will depend on the distance between pulses – That it might not be right to extrapolate the single pulse jitter from the difference by dividing it by √ 2 without correlating it with: • the effect of the memory structure • the potential dispersions between different circuits in a multi-channel system • the long term drift after time calibration if the latter was performed • This is especially true with analog memories making use of long delay lines (and even more if they are not servo-controlled) • This is much less sensitive in matrix structures where delay lines are very short , servocontrolled , and synchronized to the clock D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

The Wave Catcher on Jerry’s test bench at SLAC D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

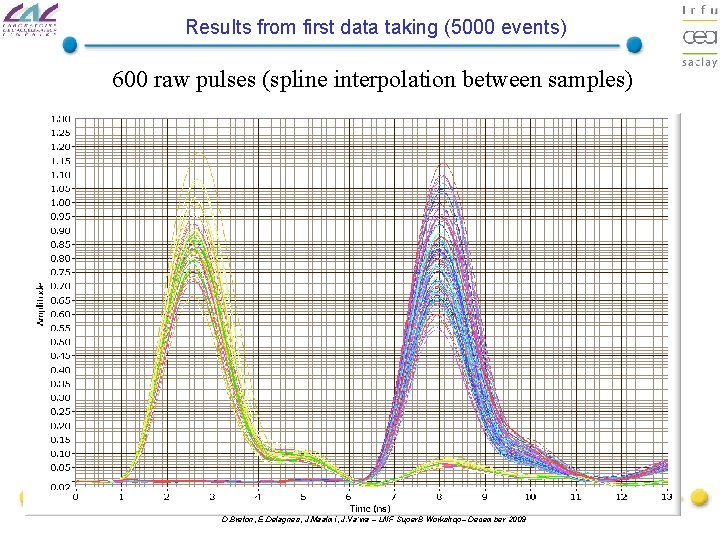
Results from first data taking (5000 events) 600 raw pulses (spline interpolation between samples) D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

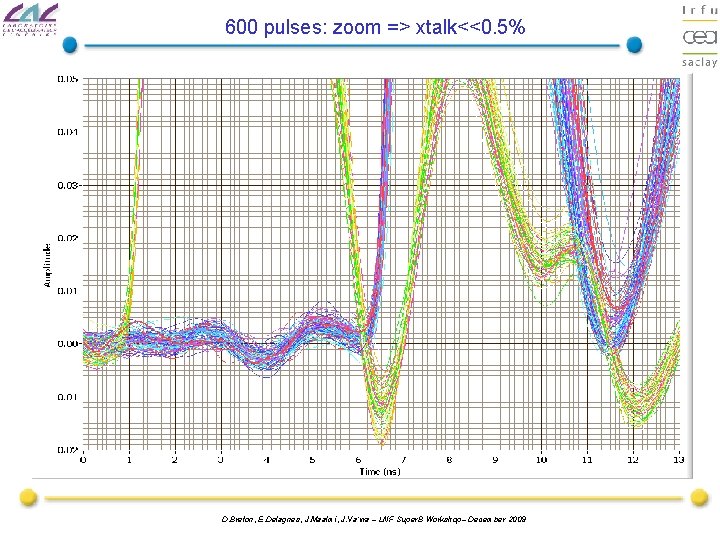
600 pulses: zoom => xtalk<<0. 5% D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

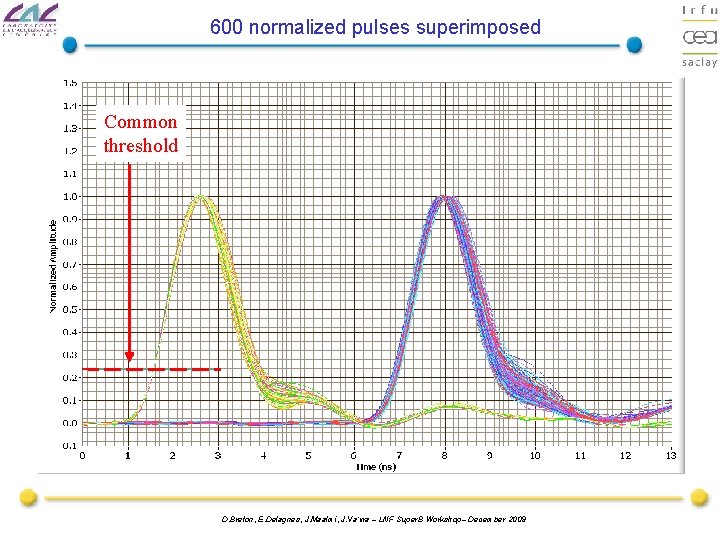
600 normalized pulses superimposed Common threshold D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

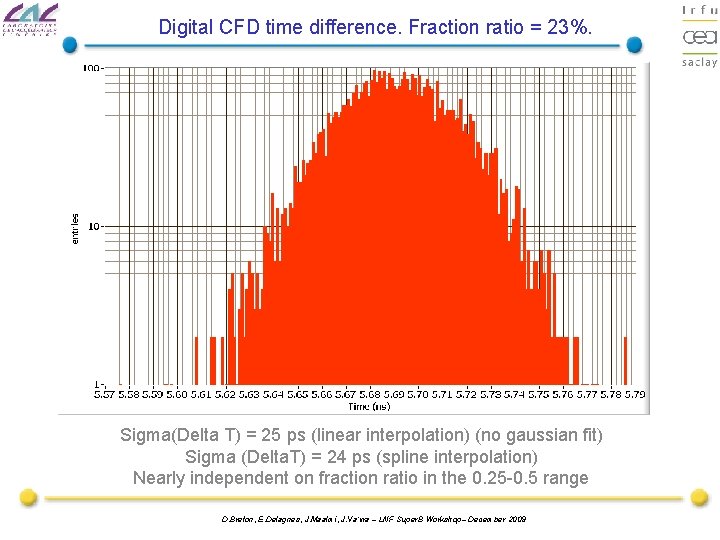
Digital CFD time difference. Fraction ratio = 23%. Sigma(Delta T) = 25 ps (linear interpolation) (no gaussian fit) Sigma (Delta. T) = 24 ps (spline interpolation) Nearly independent on fraction ratio in the 0. 25 -0. 5 range D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

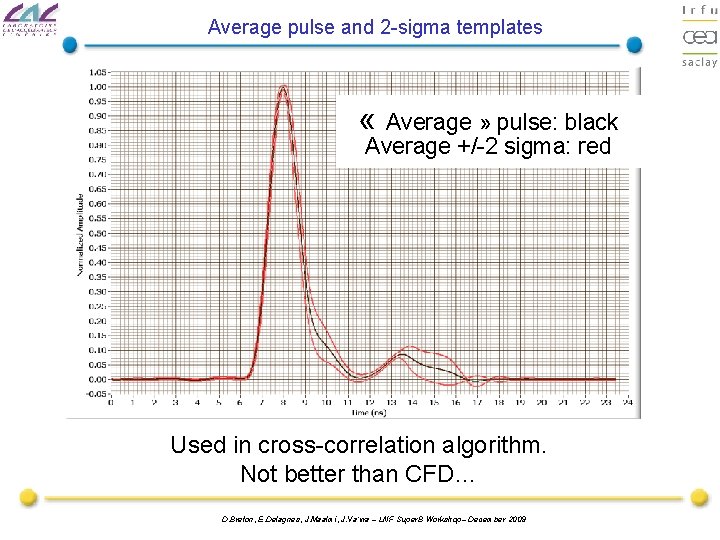
Average pulse and 2 -sigma templates « Average » pulse: black Average +/-2 sigma: red Used in cross-correlation algorithm. Not better than CFD… D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

Conclusion • The USB Wave Catcher has become a demonstrator for the use of matrix analog memories in the field of ps time measurement. • Lab timing measurements showed a single pulse resolution of ~16 ps rms without time INL correction, and less than 10 ps after correction. • The board has been tested with MCPPMT’s for low-jitter light to time conversion on Jerry’s test bench. • The first results are coherent with previous measurements (based both on Ortec and Target chip): • 24 ps for the time difference => 17 ps for a single pulse • More generally, tests showed us that analog memories look perfectly suited for ps time measurement. => no need for analog to digital pulse conversion, low power and low cost ! • Jerry will now refine these results. D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009

Summary of the board performances. • 2 DC-coupled 256 -deep channels with 50 -Ohm active input impedance • ± 1. 25 V dynamic Range, with full range 16 -bit individual tunable offsets • 2 individual pulse generators for reflectometry applications. • On-board charge integration calculation. • Bandwidth > 500 MHz • Signal/noise ratio: 11. 9 bits rms (noise = 630 µV RMS) • Sampling Frequency: 400 MS/s to 3. 2 GS/s • Max consumption on +5 V: 0. 5 A • Absolute time precision in a channel (typical): • without INL calibration: 20 ps rms (400 MS/s to 1. 6 GS/s) 16 ps rms (3. 2 GS/s) • after INL calibration 12 ps rms (400 MS/s to 1. 6 GS/s) 8 ps rms (3. 2 GS/s) • Relative time precision between channels: still to be measured. • Trigger source: software, external, internal, threshold on signals • Acquisition rate (full events) Up to ~1. 5 k. Hz over 2 full channels • Acquisition rate (charge mode) Up to ~40 k. Hz over 2 channels Acquisition software with graphical interface is now available D. Breton, E. Delagnes, J. Maalmi, J. Va’vra – LNF Super. B Workshop– December 2009