PICCOLA GUIDA PER FUNZIONI REALI A DUE VARIABILI

PICCOLA GUIDA PER FUNZIONI REALI A DUE VARIABILI Roberto Ghiselli Ricci per il corso di Metodi Quantitativi per l’Economia Università di Ferrara 2014 1

Simbologia e terminologia Una funzione f : D→ R si dice a due variabili di input se il suo dominio D è un sottoinsieme del piano cartesiano e la denoteremo come z = f(x, y). Le variabili x, y sono dette indipendenti, mentre la z dipendente. Ferrara 2014 2

Dominio di una funzione Per determinare il dominio D delle funzioni a due variabili che noi studieremo, tenete conto che: D coincide con tutto il piano se la f è una funzione razionale intera D coincide con tutto il piano esclusi i punti in cui il denominatore vale zero se la f è una funzione razionale fratta Ferrara 2014 3

Dominio di una funzione D coincide con i punti in cui l’argomento è non negativo se la f è una funzione irrazionale (radice quadrata o di indice pari) D coincide con i punti in cui l’argomento è positivo se la f è una funzione logaritmica Ferrara 2014 4

Esempi Se f(x, y)=2 x-3 y+8 allora D coincide con tutto il piano Se allora D coincide con tutto il piano esclusi i punti della circonferenza di centro l’origine e raggio 3. Ferrara 2014 5

Grafico di una funzione Il grafico di una funzione è l’insieme di tutti e soli i punti dello spazio cartesiano di coordinate (x, y, z) tali che z = f(x, y) Il grafico di una funzione rappresenta una superficie nello spazio cartesiano. Ferrara 2014 6

Esempi di grafici Ferrara 2014 7

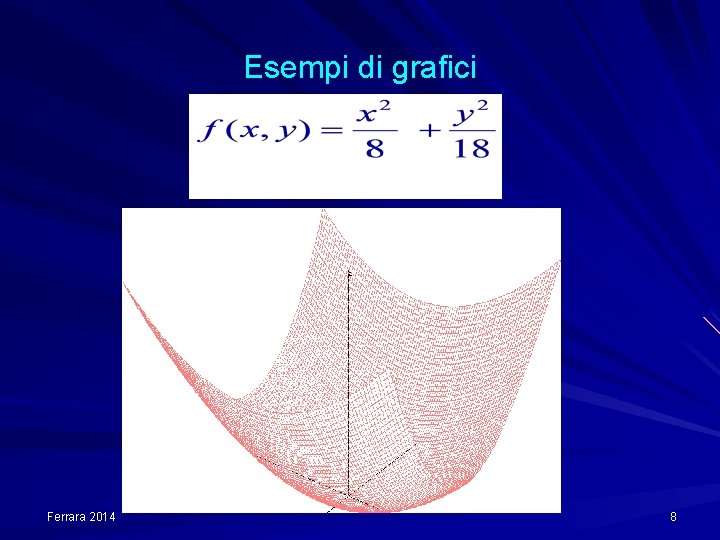
Esempi di grafici Ferrara 2014 8

Esempi di grafici Ferrara 2014 9

Disequazioni in due variabili Per determinare il dominio D di una funzione z=f(x, y), occorre in genere risolvere una disequazione a due variabili Supponiamo di rappresentare una disequazione a due variabili nella forma g(x, y)>0, ove g sia un polinomio in x e y Ferrara 2014 10

Disequazioni in due variabili L’equazione g(x, y)=0 rappresenta una curva C del piano cartesiano. Nelle situazioni semplici che noi affronteremo, tale curva dividerà il piano cartesiano in due parti ben distinte e la disequazione g(x, y)>0 sarà soddisfatta da tutti i punti di una sola di queste due parti Ferrara 2014 11

Disequazioni in due variabili Se g(x, y)=ax+by+c, con a, b 0, C è una retta e la soluzione è data dai punti che stanno in uno solo dei due semipiani generati dalla retta. Per individuare il semipiano giusto, basta scegliersi un punto a caso in uno dei due semipiani che non stia sulla retta e verificare se soddisfa la disequazione g(x, y)>0 Ferrara 2014 12

Disequazioni in due variabili Questa strategia funziona anche per le funzioni g(x, y) polinomiali che noi studieremo: prima individuate il grafico della curva C, poi provate a calcolare la g(x, y) in un punto P scelto a caso all’interno di una delle due parti di piano generate da g e controllate se g(P)>0 Ferrara 2014 13

Esempi 2 x-3 y+6>0 Ferrara 2014 14

Esempi Ferrara 2014 15

Esempi Ferrara 2014 16

Sistemi di disequazioni in due variabili L’insieme delle soluzioni di un sistema è dato dalle soluzioni comuni a tutte le disequazioni del sistema Prima risolvete le singole disequazioni e poi rappresentate le soluzioni sul piano: l’intersezione è la soluzione del sistema Ferrara 2014 17

Esercizi di verifica Ferrara 2014 18

Esercizi di verifica Determinate il dominio delle seguenti funzioni: Ferrara 2014 19

Esercizi di verifica Ferrara 2014 20