Physik fr Mediziner und Zahnmediziner Vorlesung 16 Prof

Physik für Mediziner und Zahnmediziner Vorlesung 16 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 1

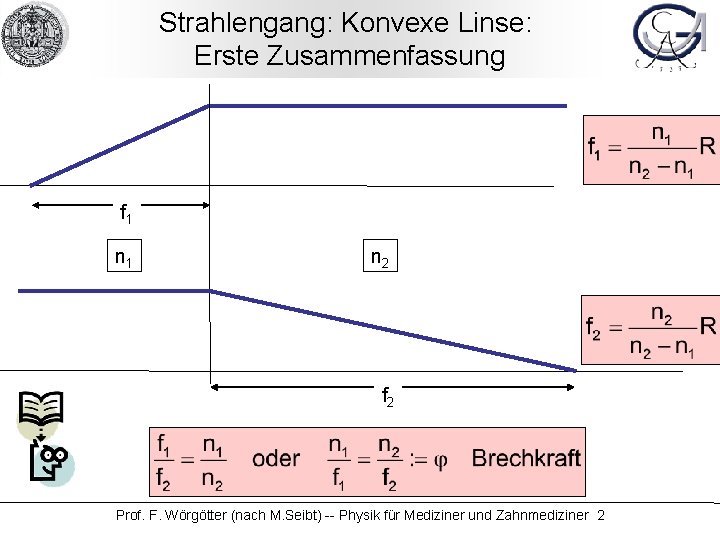
Strahlengang: Konvexe Linse: Erste Zusammenfassung f 1 n 2 f 2 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 2

Anmerkung • Achtung: – Im strengen Sinne ist all dies Wellenlängenabhängig • f 1 (und f 2) sind für verschiedene Farben verschieden (chromatische Aberration) – Des weiteren führt auch die Annahme von x=0 zu Problemen • f 1 (und f 2) sind für achsennahe und achsenferne Strahlen verschieden (sphärische Aberration) Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 3

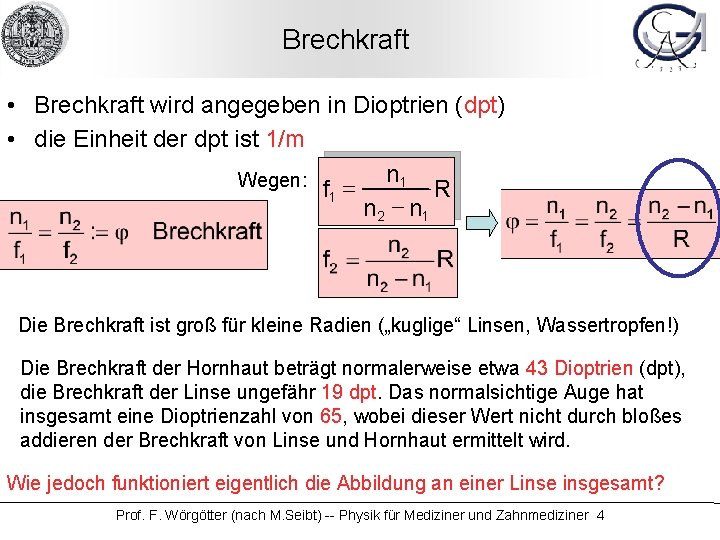
Brechkraft • Brechkraft wird angegeben in Dioptrien (dpt) • die Einheit der dpt ist 1/m Wegen: f = n 1 R 1 n 2 - n 1 Die Brechkraft ist groß für kleine Radien („kuglige“ Linsen, Wassertropfen!) Die Brechkraft der Hornhaut beträgt normalerweise etwa 43 Dioptrien (dpt), die Brechkraft der Linse ungefähr 19 dpt. Das normalsichtige Auge hat insgesamt eine Dioptrienzahl von 65, wobei dieser Wert nicht durch bloßes addieren der Brechkraft von Linse und Hornhaut ermittelt wird. Wie jedoch funktioniert eigentlich die Abbildung an einer Linse insgesamt? Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 4

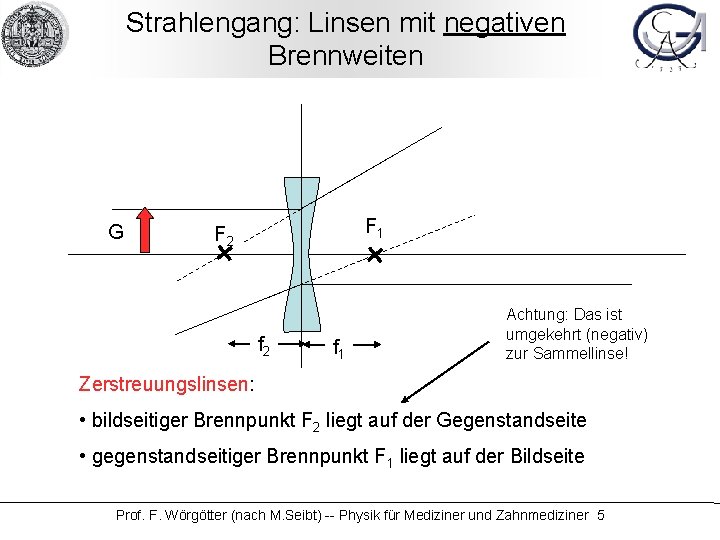
Strahlengang: Linsen mit negativen Brennweiten G F 1 F 2 f 1 Achtung: Das ist umgekehrt (negativ) zur Sammellinse! Zerstreuungslinsen: • bildseitiger Brennpunkt F 2 liegt auf der Gegenstandseite • gegenstandseitiger Brennpunkt F 1 liegt auf der Bildseite Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 5

Abbildungen Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 6

Erzeugung einer Abbildung: Versuch Lochkamera Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 7

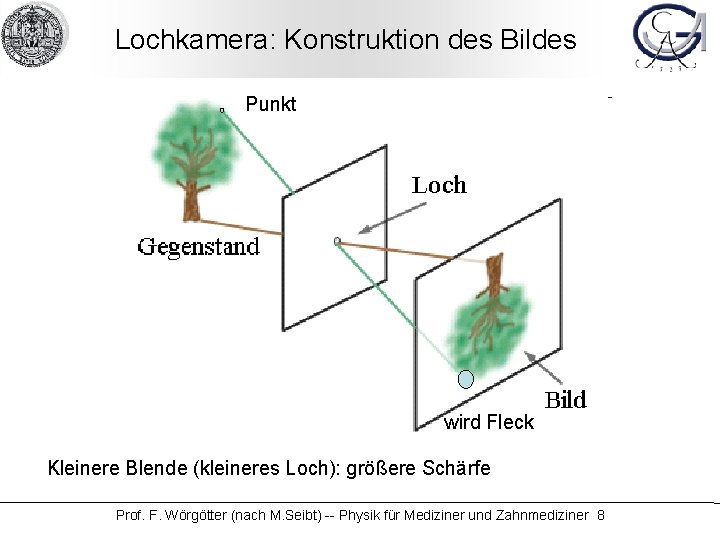
Lochkamera: Konstruktion des Bildes Punkt wird Fleck Kleinere Blende (kleineres Loch): größere Schärfe Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 8

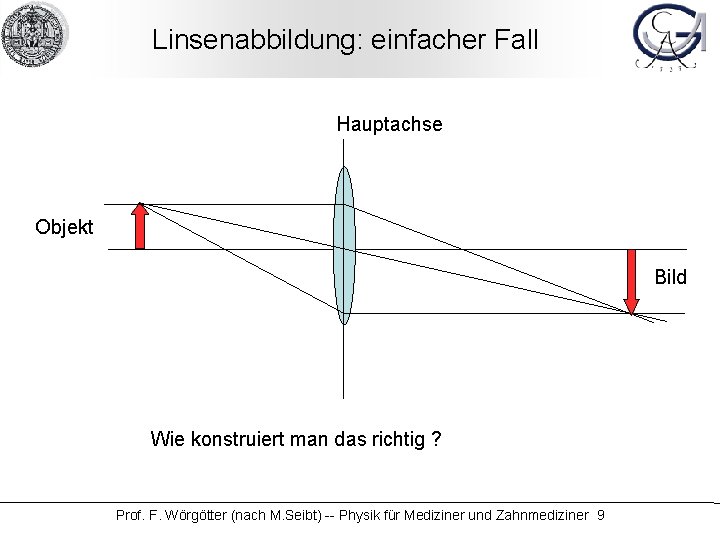
Linsenabbildung: einfacher Fall Hauptachse Objekt Bild Wie konstruiert man das richtig ? Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 9

Versuch: Linsenabbildung Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 10

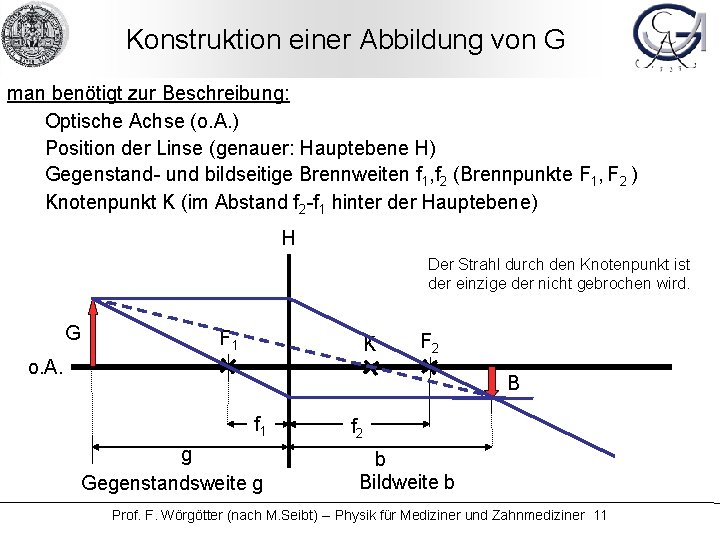
Konstruktion einer Abbildung von G man benötigt zur Beschreibung: Optische Achse (o. A. ) Position der Linse (genauer: Hauptebene H) Gegenstand- und bildseitige Brennweiten f 1, f 2 (Brennpunkte F 1, F 2 ) Knotenpunkt K (im Abstand f 2 -f 1 hinter der Hauptebene) H Der Strahl durch den Knotenpunkt ist der einzige der nicht gebrochen wird. G F 1 K o. A. F 2 B f 1 g Gegenstandsweite g f 2 b Bildweite b Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 11

Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 12

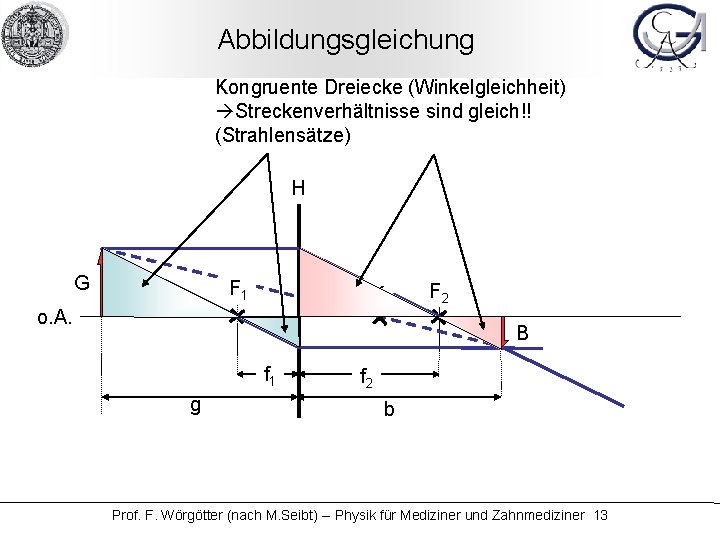
Abbildungsgleichung Kongruente Dreiecke (Winkelgleichheit) Streckenverhältnisse sind gleich!! (Strahlensätze) H G F 1 K o. A. F 2 B f 1 g f 2 b Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 13

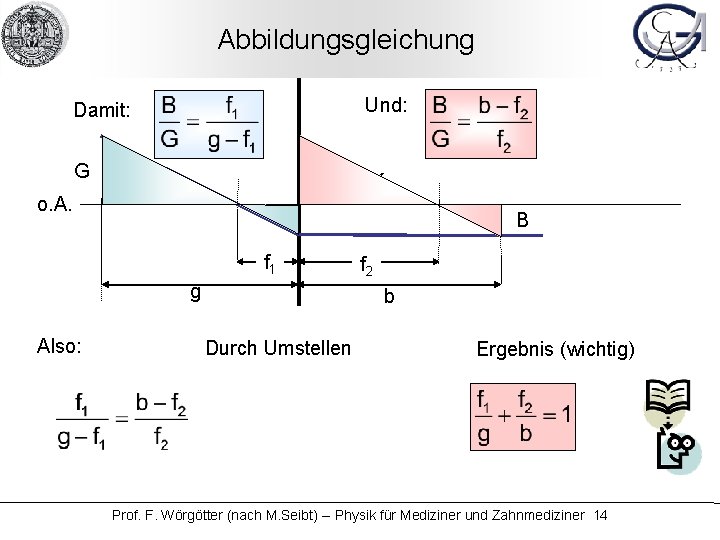
Abbildungsgleichung Und: Damit: G K o. A. B f 1 g Also: f 2 b Durch Umstellen Ergebnis (wichtig) Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 14

Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 15

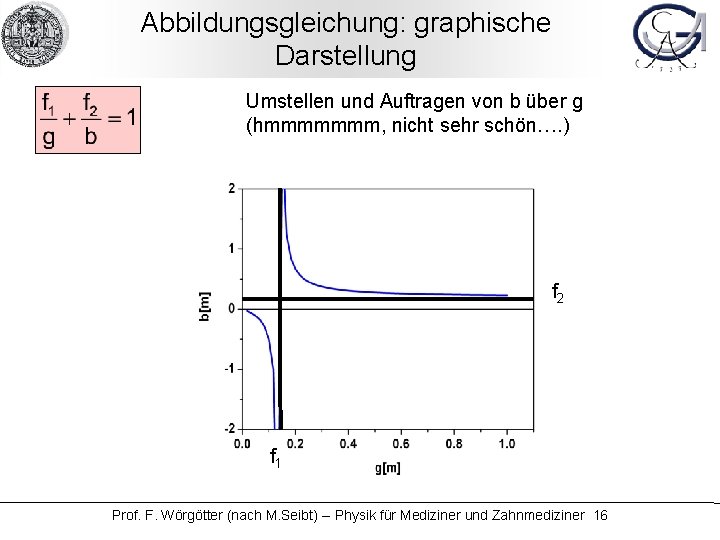
Abbildungsgleichung: graphische Darstellung Umstellen und Auftragen von b über g (hmmmmmmm, nicht sehr schön…. ) f 2 f 1 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 16

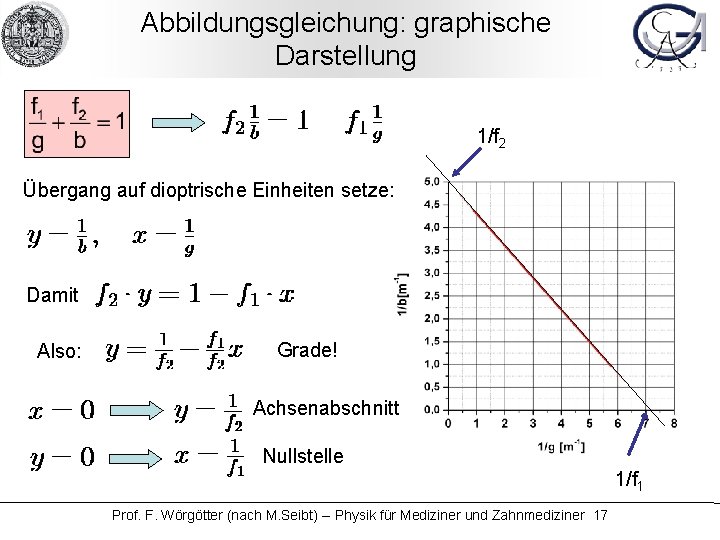
Abbildungsgleichung: graphische Darstellung 1/f 2 Übergang auf dioptrische Einheiten setze: Damit Also: Grade! Achsenabschnitt Nullstelle 1/f 1 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 17

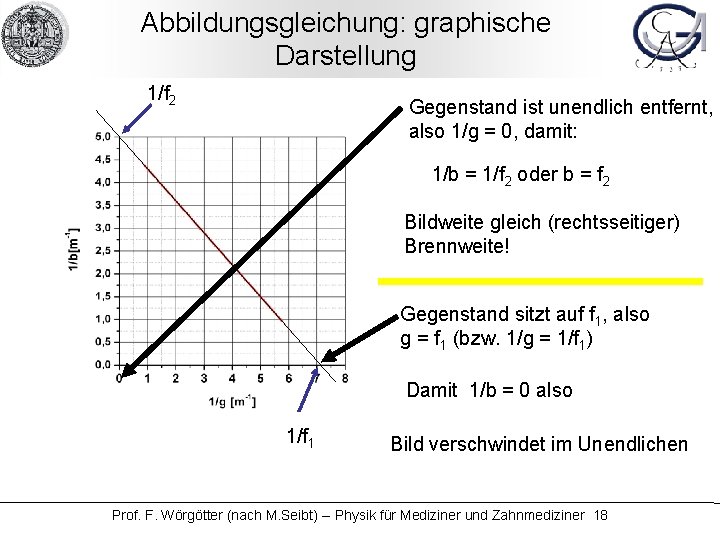
Abbildungsgleichung: graphische Darstellung 1/f 2 Gegenstand ist unendlich entfernt, also 1/g = 0, damit: 1/b = 1/f 2 oder b = f 2 Bildweite gleich (rechtsseitiger) Brennweite! Gegenstand sitzt auf f 1, also g = f 1 (bzw. 1/g = 1/f 1) Damit 1/b = 0 also 1/f 1 Bild verschwindet im Unendlichen Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 18

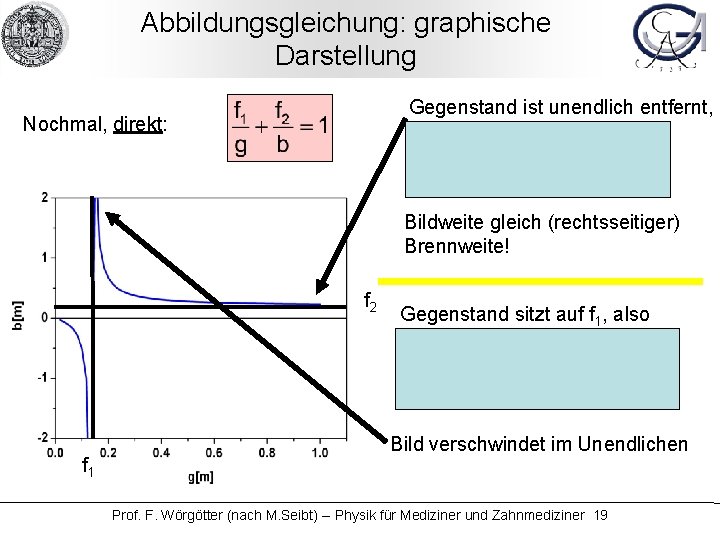
Abbildungsgleichung: graphische Darstellung Gegenstand ist unendlich entfernt, also 1/g = 0, damit: Nochmal, direkt: 1/b = 1/f 2 oder b = f 2 Bildweite gleich (rechtsseitiger) Brennweite! f 2 Gegenstand sitzt auf f 1, also g = f 1 (bzw. 1/g = 1/f 1) Damit 1/b = 0 also f 1 Bild verschwindet im Unendlichen Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 19

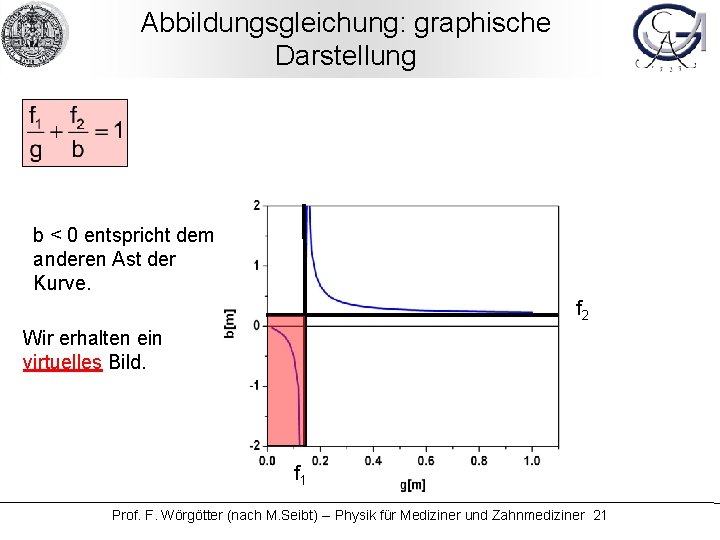
Abbildungsgleichung: graphische Darstellung Was geschieht wenn der Gegenstand näher als f 1 an der Hauptebene dran ist? Also für: g < f 1 !? Dann ist: f 1/g > 1 Somit muß b negativ werden, damit die Abbildungsgleichung erhalten bleibt. Das Bild erscheint vor (? ? ? ) der Linse. ? ? ä H Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 20

Abbildungsgleichung: graphische Darstellung b < 0 entspricht dem anderen Ast der Kurve. f 2 Wir erhalten ein virtuelles Bild. f 1 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 21

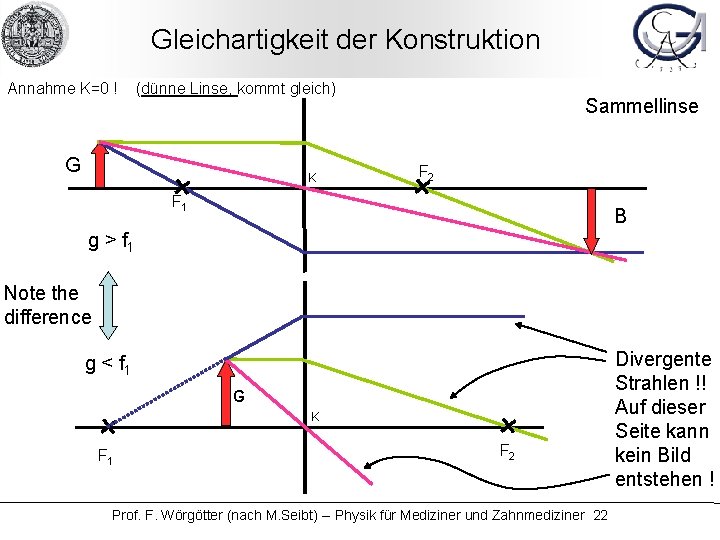
Gleichartigkeit der Konstruktion Annahme K=0 ! (dünne Linse, kommt gleich) G K Sammellinse F 2 F 1 B g > f 1 Note the difference g < f 1 G K F 1 F 2 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 22 Divergente Strahlen !! Auf dieser Seite kann kein Bild entstehen !

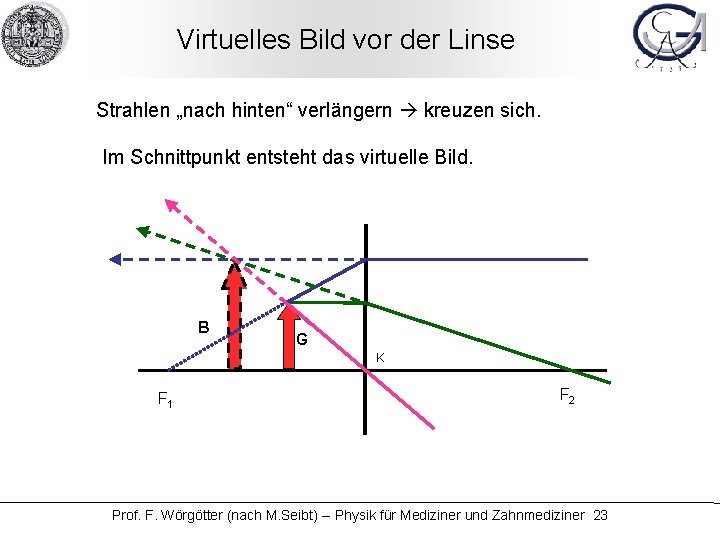
Virtuelles Bild vor der Linse Strahlen „nach hinten“ verlängern kreuzen sich. Im Schnittpunkt entsteht das virtuelle Bild. B G K F 1 F 2 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 23

Reelle und virtuelle Bilder reelles Bild: optisches Abbild, das auf einem Schirm aufgefangen werden kann virtuelles Bild: Lichtstrahlen scheinen von einem optischen Abbild zu kommen, das nicht wirklich da ist „Von dem Ort des virtuellen Bildes gehen keine Lichtstrahlen aus (daher die Bezeichnung „virtuell“), die Strahlen scheinen aber von dem Bild her zu kommen, da unsere Wahrnehmung Lichtstrahlen als geradlinig unterstellt und den ins Auge treffenden Strahl, wenn nötig, rückwärts verlängert. “(Wikipedia) Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner

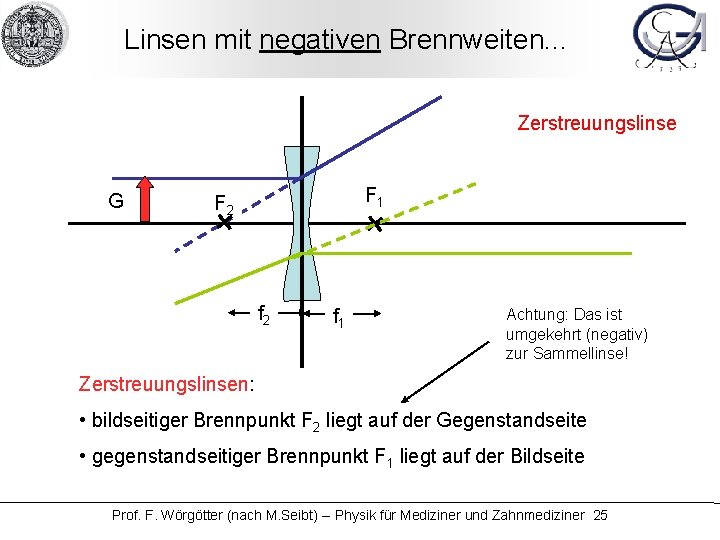
Linsen mit negativen Brennweiten. . . Zerstreuungslinse G F 1 F 2 f 1 Achtung: Das ist umgekehrt (negativ) zur Sammellinse! Zerstreuungslinsen: • bildseitiger Brennpunkt F 2 liegt auf der Gegenstandseite • gegenstandseitiger Brennpunkt F 1 liegt auf der Bildseite Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 25

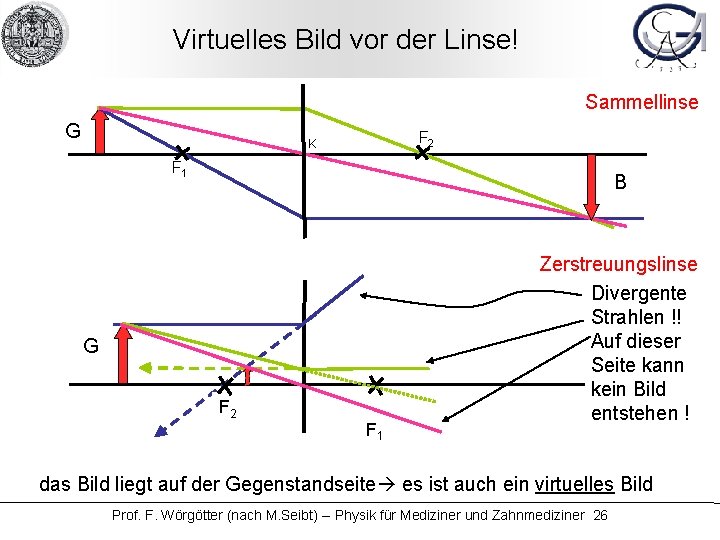
Virtuelles Bild vor der Linse! Sammellinse G F 2 K F 1 B G F 2 F 1 Zerstreuungslinse Divergente Strahlen !! Auf dieser Seite kann kein Bild entstehen ! das Bild liegt auf der Gegenstandseite es ist auch ein virtuelles Bild Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 26

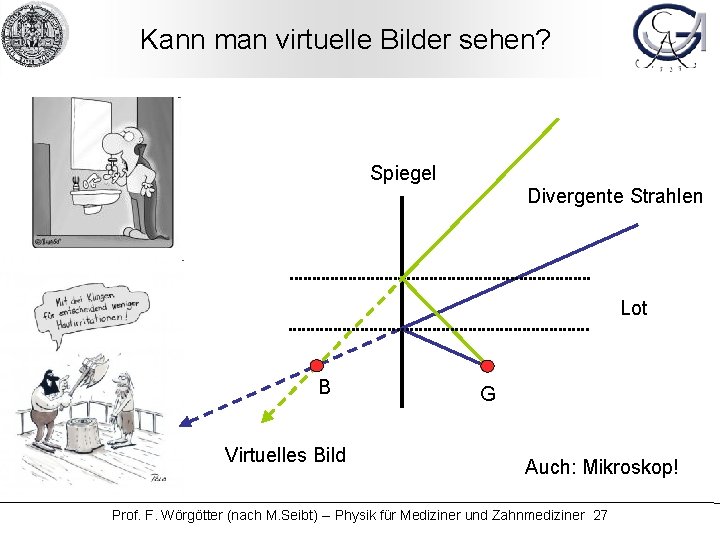
Kann man virtuelle Bilder sehen? Spiegel Divergente Strahlen Lot B Virtuelles Bild G Auch: Mikroskop! Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 27

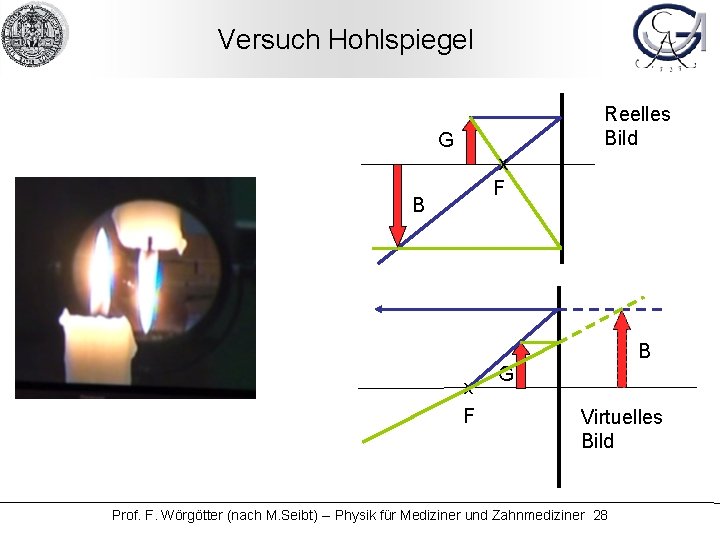
Versuch Hohlspiegel Reelles Bild G x F B B x F G Virtuelles Bild Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 28

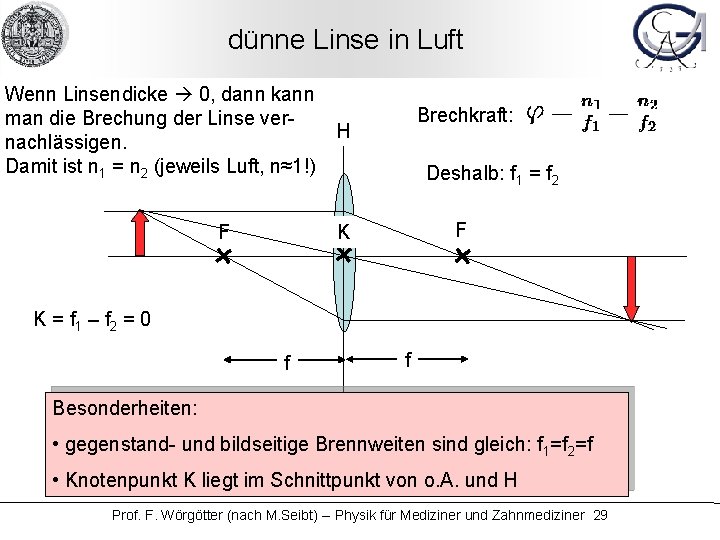
dünne Linse in Luft Wenn Linsendicke 0, dann kann man die Brechung der Linse vernachlässigen. Damit ist n 1 = n 2 (jeweils Luft, n≈1!) F Brechkraft: H Deshalb: f 1 = f 2 F K K = f 1 – f 2 = 0 f f Besonderheiten: • gegenstand- und bildseitige Brennweiten sind gleich: f 1=f 2=f • Knotenpunkt K liegt im Schnittpunkt von o. A. und H Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 29

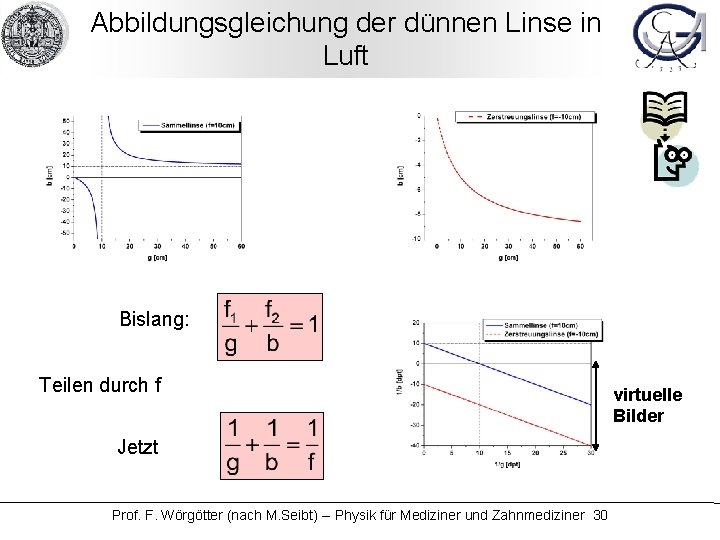
Abbildungsgleichung der dünnen Linse in Luft Bislang: Teilen durch f Jetzt Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 30 virtuelle Bilder

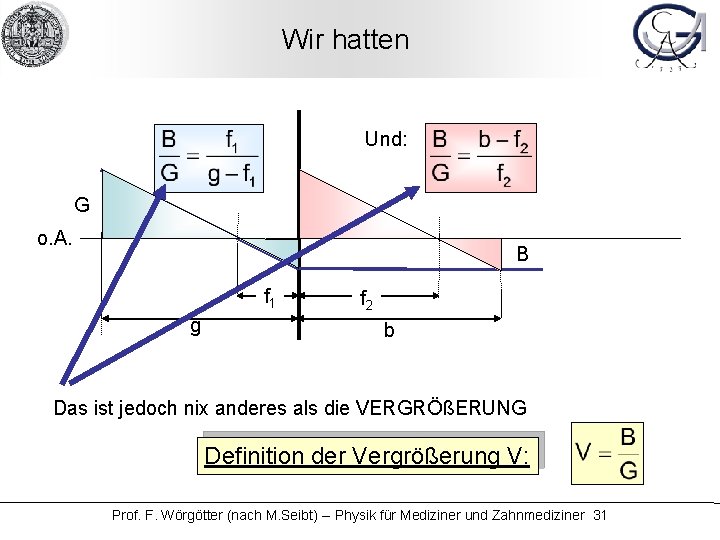
Wir hatten Und: G K o. A. B f 1 g f 2 b Das ist jedoch nix anderes als die VERGRÖßERUNG Definition der Vergrößerung V: Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 31

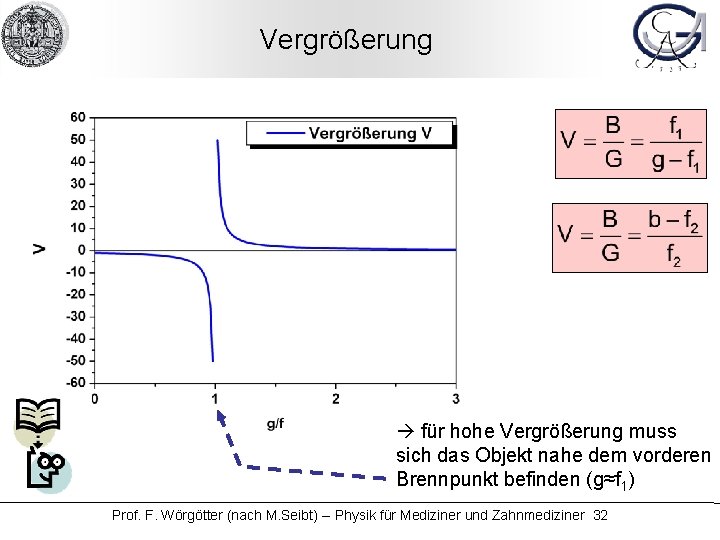
Vergrößerung für hohe Vergrößerung muss sich das Objekt nahe dem vorderen Brennpunkt befinden (g≈f 1) Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 32

Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 33

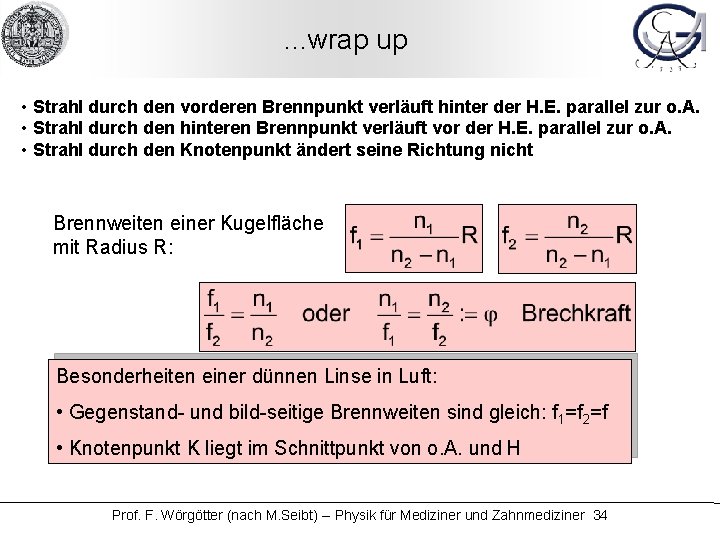
. . . wrap up • Strahl durch den vorderen Brennpunkt verläuft hinter der H. E. parallel zur o. A. • Strahl durch den hinteren Brennpunkt verläuft vor der H. E. parallel zur o. A. • Strahl durch den Knotenpunkt ändert seine Richtung nicht Brennweiten einer Kugelfläche mit Radius R: Besonderheiten einer dünnen Linse in Luft: • Gegenstand- und bild-seitige Brennweiten sind gleich: f 1=f 2=f • Knotenpunkt K liegt im Schnittpunkt von o. A. und H Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 34

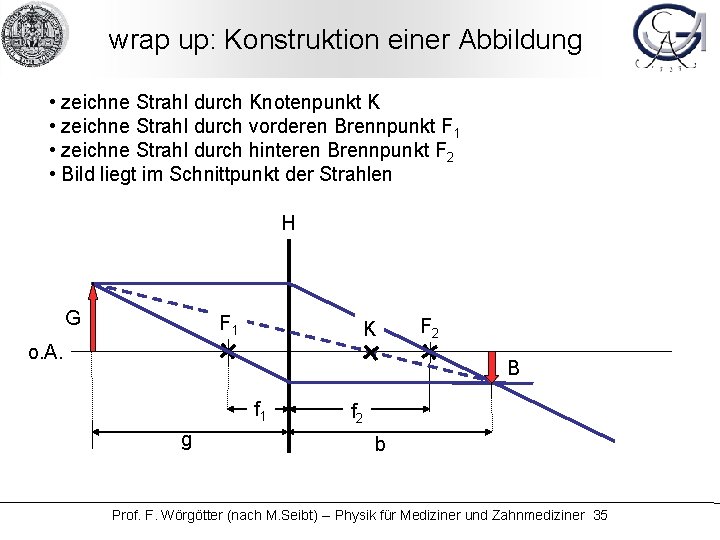
wrap up: Konstruktion einer Abbildung • zeichne Strahl durch Knotenpunkt K • zeichne Strahl durch vorderen Brennpunkt F 1 • zeichne Strahl durch hinteren Brennpunkt F 2 • Bild liegt im Schnittpunkt der Strahlen H G F 1 K o. A. F 2 B f 1 g f 2 b Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 35

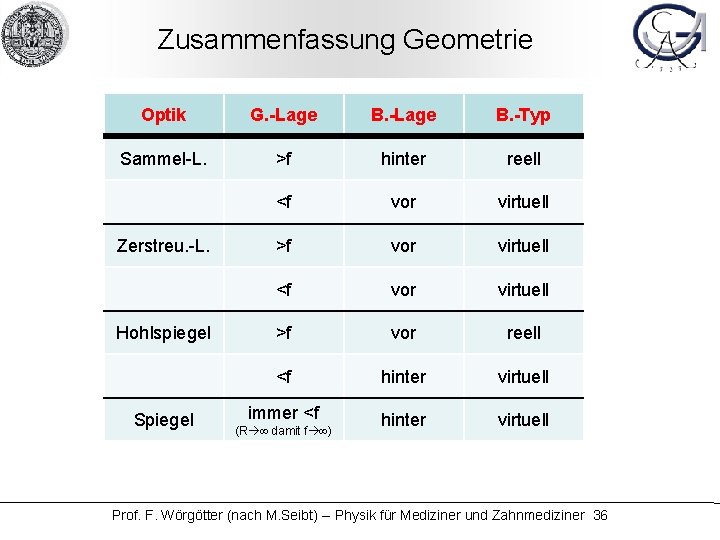
Zusammenfassung Geometrie Optik G. -Lage B. -Typ Sammel-L. >f hinter reell <f vor virtuell >f vor virtuell <f vor virtuell >f vor reell <f hinter virtuell immer <f hinter virtuell Zerstreu. -L. Hohlspiegel Spiegel (R damit f ) Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 36

Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 37

Optik des Auges Elektromagnetische Strahlung mit Wellenlängen von 400 -750 nm empfinden wir als Licht. Die Lichtstrahlen müssen zur Bildenststehung im Auge gebrochen und auf der Netzhaut scharf abgebildet werden. Dazu trägt die Hornhaut den größten Teil der Brechkraft bei, die Linse ermöglicht zusätzlich durch Änderung der Krümmung die Scharfeinstellung auf verschiedene Entfrenungen. Fehlsichtigkeiten (. . . ) beruhen auf Missverhältnissen zwischen der Brechkraft des Auges und Länge des Augapfels. Die Pupille wirkt als variable Blende, verringert Abbildungsfehler und reguliert den Lichteinfall. Die Form des Auges wird durch den Augeninnendruck aufrechterhalten. . aus: Klinke/Silbernagel „Lehrbuch der Physiologie“ Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 38

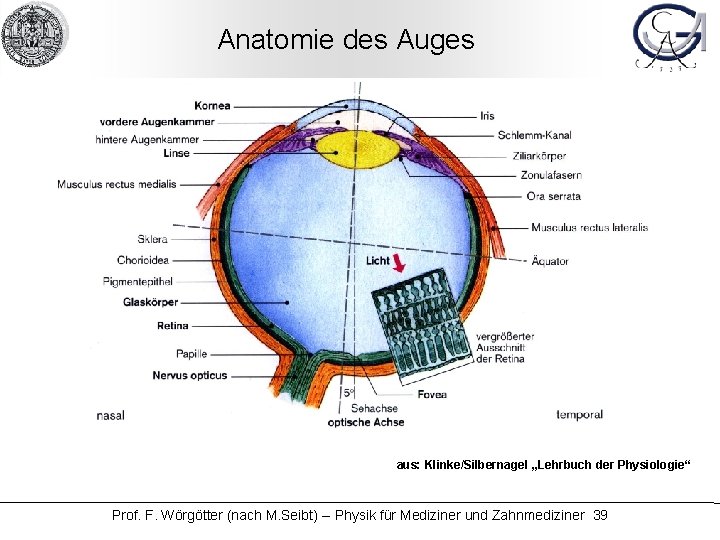
Anatomie des Auges aus: Klinke/Silbernagel „Lehrbuch der Physiologie“ Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 39

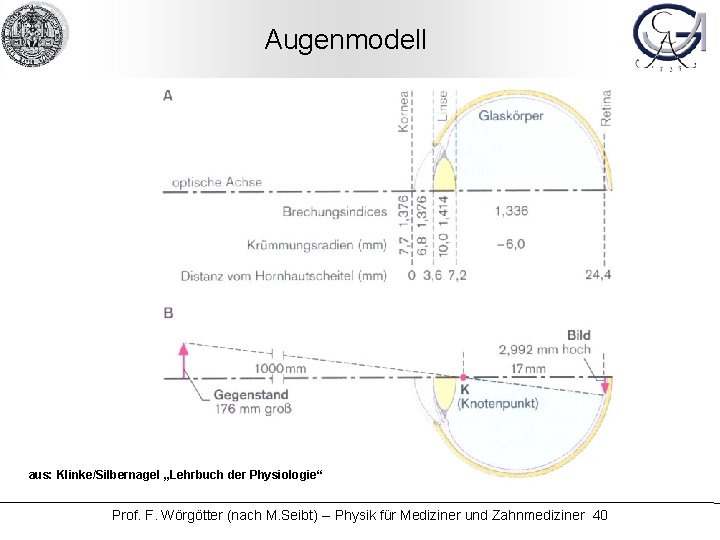
Augenmodell aus: Klinke/Silbernagel „Lehrbuch der Physiologie“ Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 40

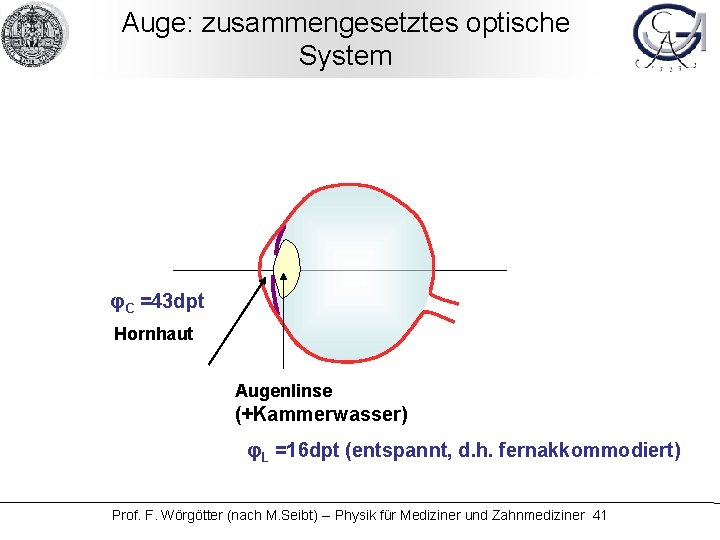
Auge: zusammengesetztes optische System φC =43 dpt Hornhaut Augenlinse (+Kammerwasser) φL =16 dpt (entspannt, d. h. fernakkommodiert) Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 41

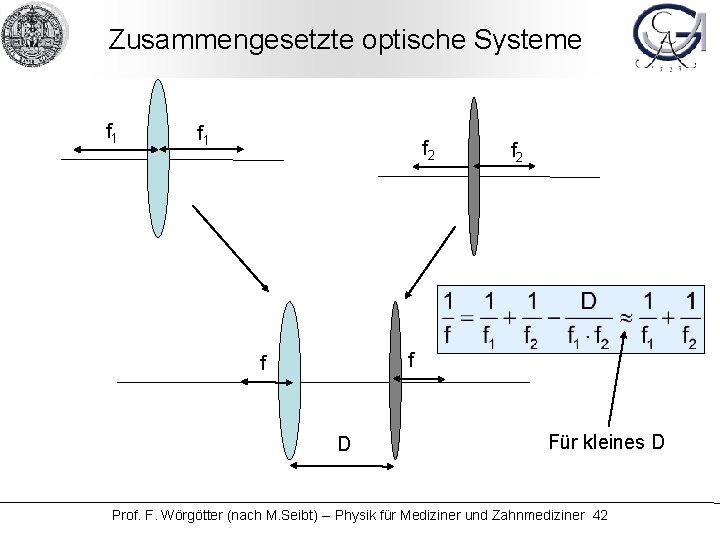
Zusammengesetzte optische Systeme f 1 f 2 f f D Für kleines D Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 42

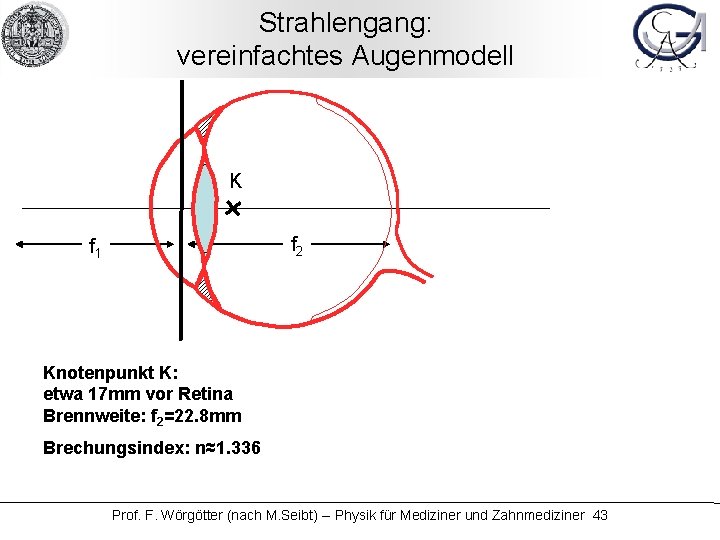
Strahlengang: vereinfachtes Augenmodell K f 2 f 1 Knotenpunkt K: etwa 17 mm vor Retina Brennweite: f 2=22. 8 mm Brechungsindex: n≈1. 336 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 43

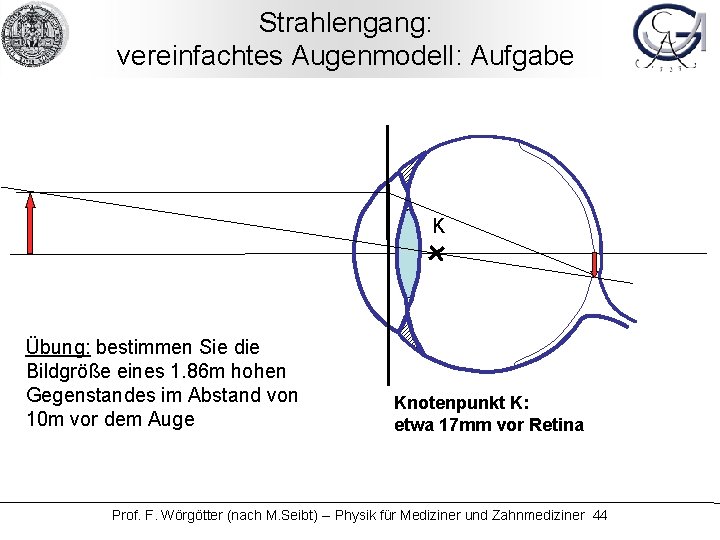
Strahlengang: vereinfachtes Augenmodell: Aufgabe K Übung: bestimmen Sie die Bildgröße eines 1. 86 m hohen Gegenstandes im Abstand von 10 m vor dem Auge Knotenpunkt K: etwa 17 mm vor Retina Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 44

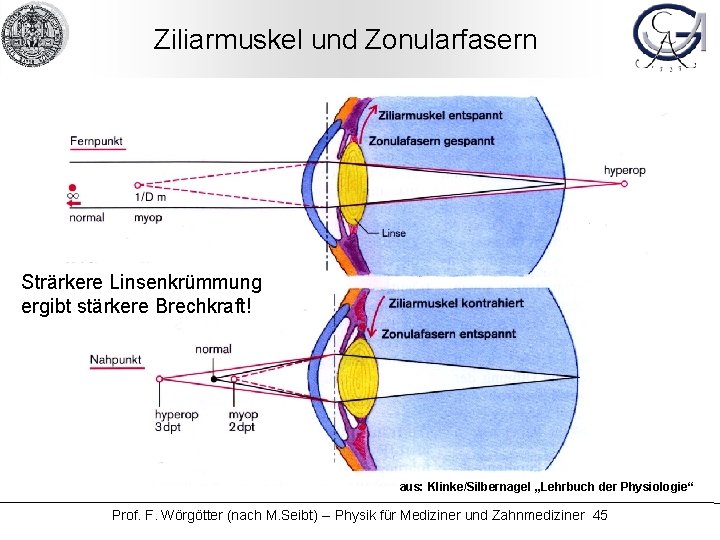
Ziliarmuskel und Zonularfasern Strärkere Linsenkrümmung ergibt stärkere Brechkraft! aus: Klinke/Silbernagel „Lehrbuch der Physiologie“ Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 45

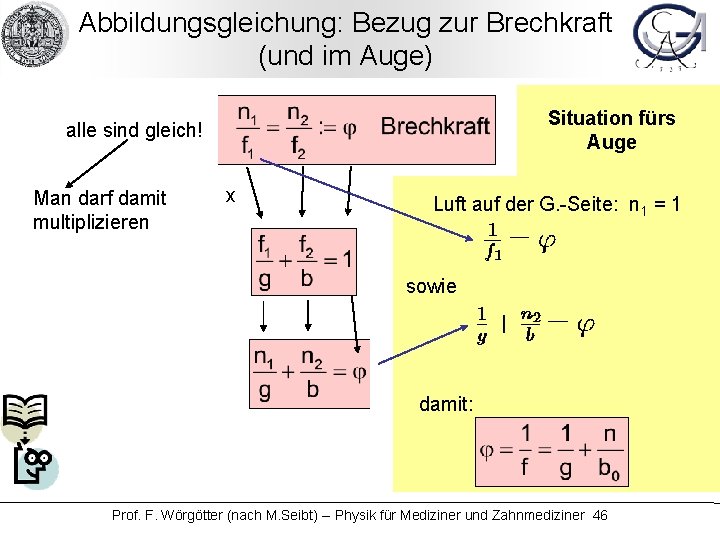
Abbildungsgleichung: Bezug zur Brechkraft (und im Auge) Situation fürs Auge alle sind gleich! Man darf damit multiplizieren x Luft auf der G. -Seite: n 1 = 1 sowie damit: Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 46

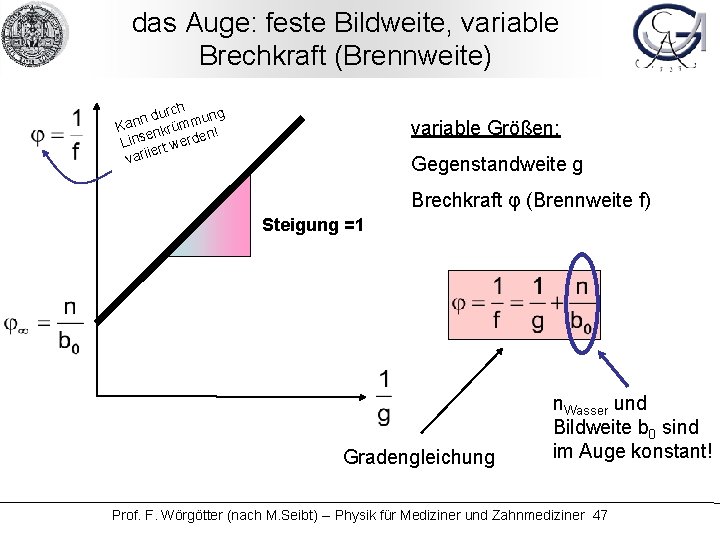
das Auge: feste Bildweite, variable Brechkraft (Brennweite) h durc mung n n Ka nkrüm n! e Lins rt werde e varii variable Größen: Gegenstandweite g Brechkraft φ (Brennweite f) Steigung =1 Gradengleichung n. Wasser und Bildweite b 0 sind im Auge konstant! Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 47

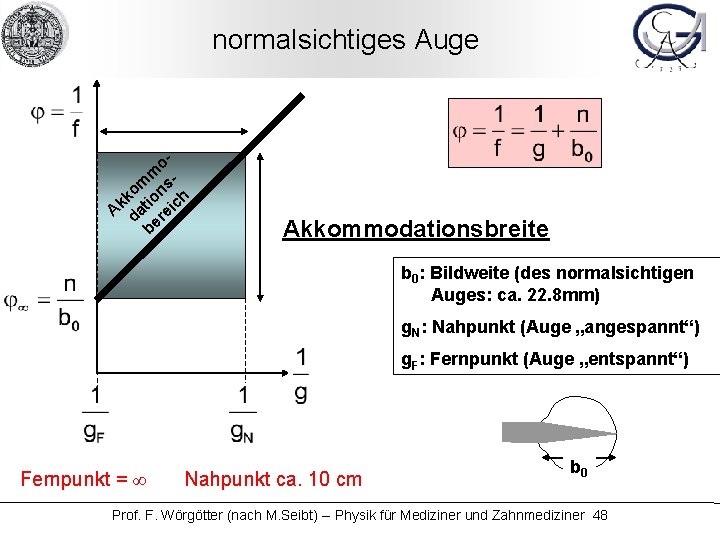
normalsichtiges Auge om m o ons h k k i A dat reic be Akkommodationsbreite b 0: Bildweite (des normalsichtigen Auges: ca. 22. 8 mm) g. N: Nahpunkt (Auge „angespannt“) g. F: Fernpunkt (Auge „entspannt“) Fernpunkt = ∞ Nahpunkt ca. 10 cm b 0 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 48

Akkommodation Experimente weit entfernter Gegenstand Beobachtung: Deutung: naher Gegenstand Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 49

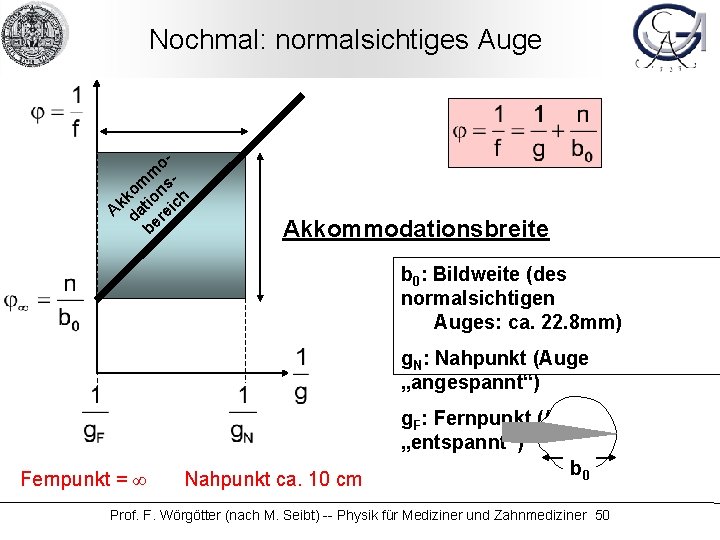
Nochmal: normalsichtiges Auge om m o ons h k k i A dat reic be Akkommodationsbreite b 0: Bildweite (des normalsichtigen Auges: ca. 22. 8 mm) g. N: Nahpunkt (Auge „angespannt“) Fernpunkt = ∞ Nahpunkt ca. 10 cm g. F: Fernpunkt (Auge „entspannt“) b 0 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 50

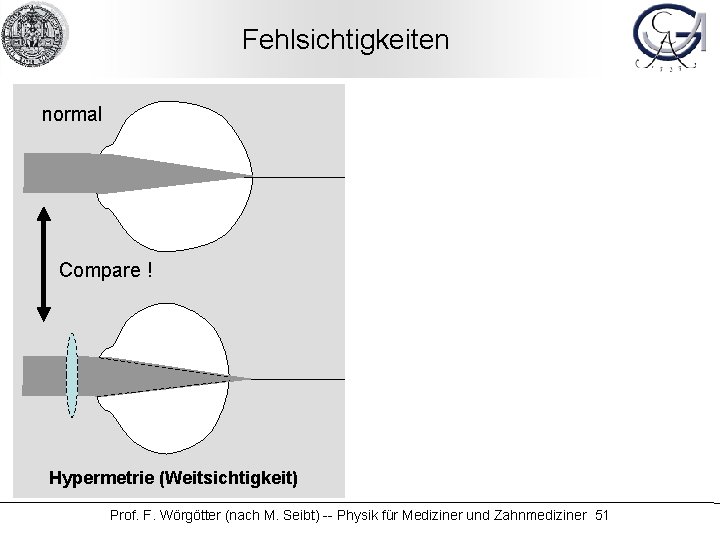
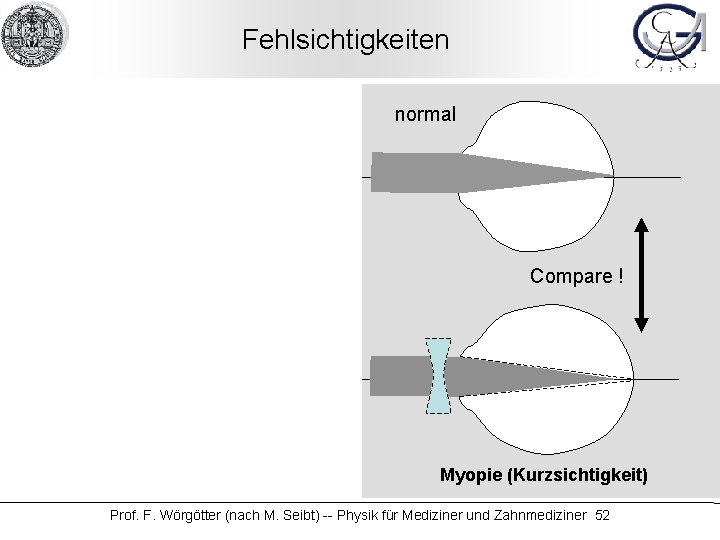
Fehlsichtigkeiten normal Compare ! Hypermetrie (Weitsichtigkeit) Compare ! Myopie (Kurzsichtigkeit) Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 51

Fehlsichtigkeiten normal Compare ! Hypermetrie (Weitsichtigkeit) Compare ! Myopie (Kurzsichtigkeit) Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 52