Physicsinspired computer algorithms Liliana Teodorescu Physics vs Computer

Physics-inspired computer algorithms Liliana Teodorescu

Physics vs Computer Science/Engineering Physics and Computer Science/Engineering have long established mutually beneficial links Computer Science/Engineering to Physics - Tools to support progress in physics (and science, in general) research Physics to Computer Science/Engineering - development of semiconductor-based computer technology based on solidstate physics - challenging environments/data – (extreme) test beds for hardware/software pushing up their developments (e. g. CERN Open. Lab activities) - advanced algorithms benefit from mathematical models of physical phenomena - topic of this lecture 2

Outline Basics of combinatorial optimisation Examples of algorithms inspired by physics - fundamental physics concepts used in the algorithm - the basics of the algorithm - some applications Concluding remarks on the benefits and concerns related to these algorithms 3

Optimisation problem Combinatorial optimisation – finding min or max value of a function of many independent variables This function is a quantitative measure of the “quality” of the system cost function or objective function Cost function - depends of the configuration of the many parts of the system - exact solution can be found only for systems with relatively small number of components - for practical solutions – use heuristic methods (provide satisfactory solution, no guarantee to be perfect or optimal) 4

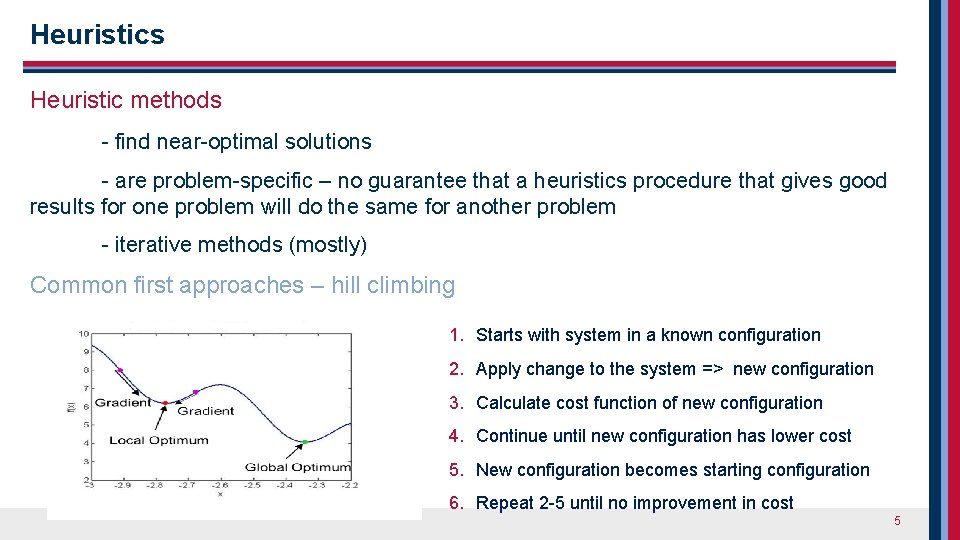
Heuristics Heuristic methods - find near-optimal solutions - are problem-specific – no guarantee that a heuristics procedure that gives good results for one problem will do the same for another problem - iterative methods (mostly) Common first approaches – hill climbing 1. Starts with system in a known configuration 2. Apply change to the system => new configuration 3. Calculate cost function of new configuration 4. Continue until new configuration has lower cost 5. New configuration becomes starting configuration 6. Repeat 2 -5 until no improvement in cost 5

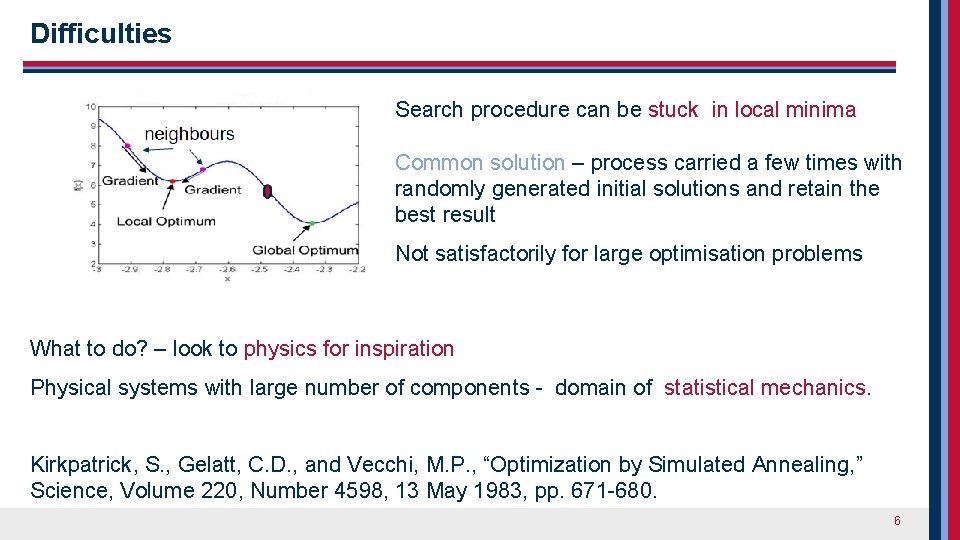
Difficulties Search procedure can be stuck in local minima Common solution – process carried a few times with randomly generated initial solutions and retain the best result Not satisfactorily for large optimisation problems What to do? – look to physics for inspiration Physical systems with large number of components - domain of statistical mechanics. Kirkpatrick, S. , Gelatt, C. D. , and Vecchi, M. P. , “Optimization by Simulated Annealing, ” Science, Volume 220, Number 4598, 13 May 1983, pp. 671 -680. 6

Statistical mechanics 7

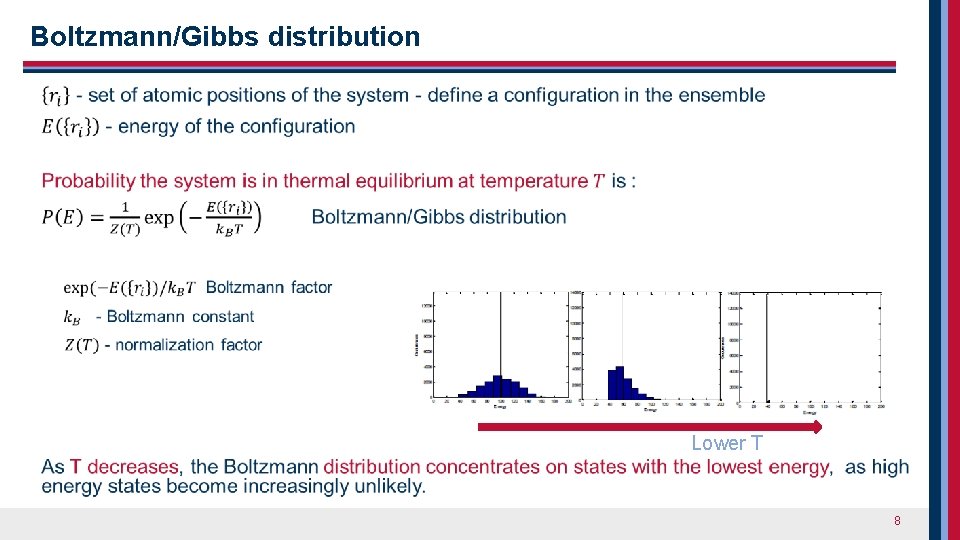
Boltzmann/Gibbs distribution Lower T 8

Annealing In practice – finding the ground state requires annealing (not just lowering the temperature) - first melt the substance - then lower the temperature slowly - at each temperature the system is allowed to reach thermal equilibrium - spend a long time at temperatures close to the freezing point Without annealing, the substance will go into a metastable state Example for a crystal lowering the temperature without annealing => a crystal with many defects 9

Statistical mechanics vs Combinatorial optimisation Statistical mechanics Combinatorial optimisation • Describe the behaviour of a physical system with many components • Describes the search for the optimal solution of a function with many variables • Describes the process of reaching the lowest energy level • Describes the algorithm to search for the minimum of the cost function • Annealing process generates stable ground states • Algorithm that simulates the annealing process likely to find an optimal minimum Simulated Annealing Algorithm System state Energy Temperature Change of state Ground state Candidate solution Cost function value Control parameter (same units as cost function) Neighbouring solution Optimal solution 10

Metropolis algorithm From early days of scientific computing - a simple algorithm to simulation a collection of atoms in equilibrium at a given temperature Metropolis, N. , A. Rosenbluth, M. Rosenbluth, A. Teller, E. Teller, "Equation of State Calculations by Fast Computing Machines", J. Chem. Phys. , 21, 6, 1087 -1092, 1953. Metropolis algorithm - based on statistical mechanics - generalization of the iterative improvement of the solution by incorporating uphill steps in the search process => better solutions 11

Metropolis algorithm (cont. ) 12

Annealing simulation Annealing - use initially high temperatures - reduce temperatures in slow stages until there are no further changes in the system - at each temperature the simulation proceed long enough for the system to reach a steady state Annealing schedule – the sequence of temperatures and the number of rearrangements of the configurations at each temperature T = αT, where α is a constant slightly less than 1 (e. g 0. 8 - 0. 99) High T => the algorithm discover the gross features of the search space Low T => the algorithm discover the fine details of the search space 13

Simulated Annealing Algorithm 14

Applications Some applications in particle physics A software implementation available in TMVA • Measurement of |V_ub| using inclusive B -> X_u l nu decays with a novel X_u-reconstruction method, H. Kakuno, Belle Coll. , ar. Xiv: hep-ex/0311048 and H. Kakuno’s Ph. D. thesis X_u reconstraction – inspired by Simulated Annealing • Supersymmetry Parameter Analysis with Fittino P. Bechtle, K. Desch, W. Porod, P. Wienemann, ar. Xiv: hep-ph/0506244 • Simulated annealing for generalized Skyrme models, J. -P. Longpre, L. Marleau, ar. Xiv: hep-ph/0502253 15

Other way of describing the world – quantum physics Can it help? 16

Quantum Annealing - inspired by Simulated Annealing - based on quantum mechanics’ formalism - also used to solve optimisation problems - first version proposed in Kadowaki T, Nishimori H. Quantum annealing in the transverse Ising model. Phys. Rev. E 1998; 58(5): 5355 -5363. 17

Quantum system State vector – state of the system at time t Schrödinger equation – describe the evolution in time of the system - Hamiltonian (operator) generates the time evolution of quantum states Given the state at an initial time (t = 0), we obtain the state at any subsequent time by solving this equation. If Hamiltonian is independent of time evolution operator, or propagator of the quantum system 18

Quantum mechanics vs optimisation problem An optimisation problem can be treated as a quantum system Candidate solution – the analogue of the quantum state vector The candidate solution evolves in time in agreement with the Schrodinger equation Transition from one candidate solution to another is made with the operator U 19

Hamiltonian – operator corresponding to the total energy of the system (sum of the kinetic and potential energy) Free particle The particle is not bound by any potential energy, so the potential energy is zero For one dimension: Particle in a region of constant potential (no dependence of space or time) For one dimension 20

Ising model Mathematical model of ferromagnetism (magnets) in statistical mechanics. - Spins of the atoms arranged in a lattice - Each spin interacts with its nearest neighbours and with an external magnetic field Hamiltonian Pauli matrices External magnetic field Magnetic moment Parameter describing the interaction between spins 21

Quantum Annealing 22

Quantum Annealing Г - is a function of time => the intensity of the external field will change in time - is intense at the beginning and gradually decrease as the algorithm is executed If the system evolves very slowly, it will eventually reach a final ground state that, with a certain probability, will correspond to the optimal value of the function encoded (cost/objective function) Quantum Computers - computer systems that implement a quantum annealing algorithm in hardware not discussed in this lecture 23

Simulated Quantum Annealing Exact implementation of a quantum annealing process on a digital computer is costly. Use simulations instead => Simulated quantum annealing (SQA) SQA - classical algorithm that uses Quantum Monte Carlo methods to simulate quantum annealing Hamiltonians (to perform calculations necessary for solving the Schrödinger equation) SQA can be exponentially faster than SA for some problems 24

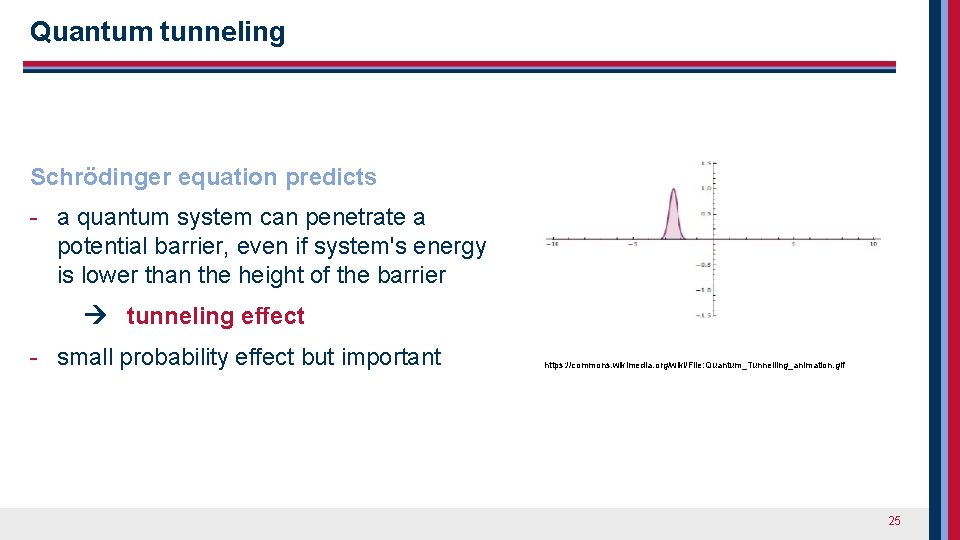
Quantum tunneling Schrödinger equation predicts - a quantum system can penetrate a potential barrier, even if system's energy is lower than the height of the barrier tunneling effect - small probability effect but important https: //commons. wikimedia. org/wiki/File: Quantum_Tunnelling_animation. gif 25

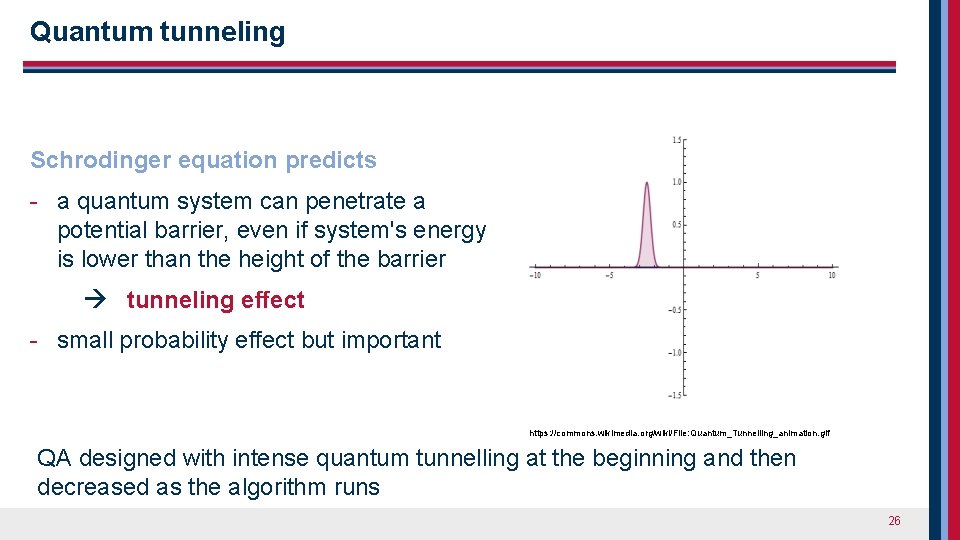
Quantum tunneling Schrodinger equation predicts - a quantum system can penetrate a potential barrier, even if system's energy is lower than the height of the barrier tunneling effect - small probability effect but important https: //commons. wikimedia. org/wiki/File: Quantum_Tunnelling_animation. gif QA designed with intense quantum tunnelling at the beginning and then decreased as the algorithm runs 26

SQA vs SA SQA can be exponentially faster than SA for some problems Theor. Int. Appl, . , 45 (2011) 99 -119 SQA outperforms SA when the cost function landscape has very high but thin barriers surrounded by shallow local minima 27

Applications A few very recent applications in particle physics • Charged particle tracking with quantum annealing-inspired optimization, A. Zlokapa et. al. , ar. Xiv: 1908. 04475 • Unfolding as Quantum Annealing , K. Cormier, R. Di Sipio, P. Wittek, ar. Xiv: 1908. 08519 • Quantum Algorithms for Jet Clustering, A. Y. Wei, P. Naik, A. W. Harrow, J. Thaler, ar. Xiv: 1908. 08949 28

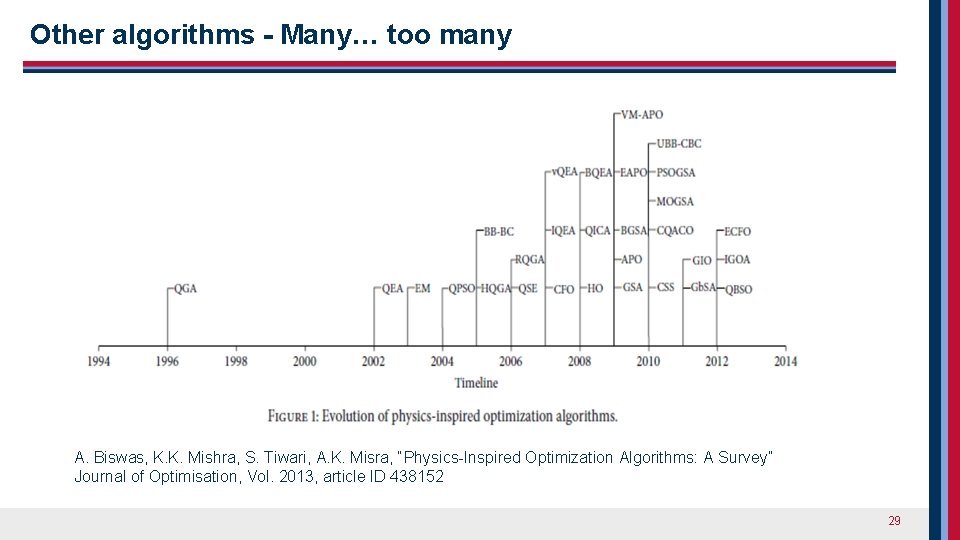
Other algorithms - Many… too many A. Biswas, K. K. Mishra, S. Tiwari, A. K. Misra, “Physics-Inspired Optimization Algorithms: A Survey” Journal of Optimisation, Vol. 2013, article ID 438152 29

Concerns and criticisms 30

Originality! 31

Conclusions Physics - is a source of inspiration for computer science algorithms for a long time - has generated very competitive algorithms - Simulated Annealing – one of the most studied algorithms - Quantum Annealing – at the origin of a different computing paradigm, Quantum Computing - Other interesting (and some not that interesting !) algorithms Be inspired to explore some of these algorithms and …why not … develop your own (a good one!) 32