Physics Vectors Objectives Graphical Method Vector Addition Relative

Physics Vectors Objectives Graphical Method Vector Addition Relative Velocity

Vectors and Scalars 1. 3. 1 Distinguish between vector and scalar quantities, and give examples of each. method. A vector is represented in print by a bold italicized symbol, for example, F. A vector has magnitude as well as direction. Some vector quantities: displacement, velocity, force, momentum A scalar has only a magnitude. Some scalar quantities: mass, time, temperature

1. The length of the line represents the magnitude and the arrow indicates the direction. 2. The magnitude and direction of the vector is clearly labeled. Tail Head

Scaling!!! The magnitude of a vector in a scaled vector diagram is depicted by the length of the arrow. The arrow is drawn precisely to length in accordance with a chosen scale.

Compass Coordinate System Direction!!! Sometimes vectors will be directed due East or due North. However we will encounter vectors in all sorts of directions and be forced to find the angle!

Compass Coordinate System • • Use the same scale for all vector magnitudes Δx = 30 m @ 20º E of N V = 20 m/s @ 30º W of N a = 10 m/s 2@ 40º W of S F = 50 N @ 10º S of E N E W To Draw direction: Ex. 20º E of N: Start w/ North and go 20° East Navigational System? S

Vector Addition – Taking two component vectors and finding the resultant. Vector Resolution – Taking a resultant vector and finding the x and y components. Sometimes uses trig. Identities to

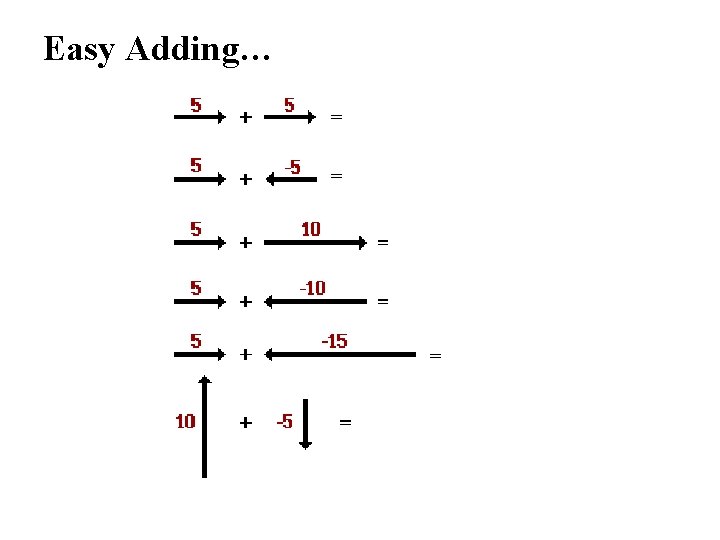
Easy Adding…

Finding Angles or Finding Sides with angle

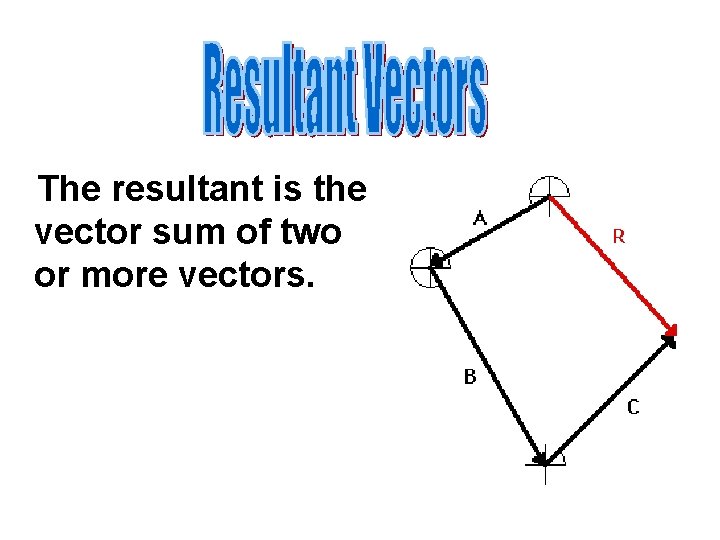
The resultant is the vector sum of two or more vectors.

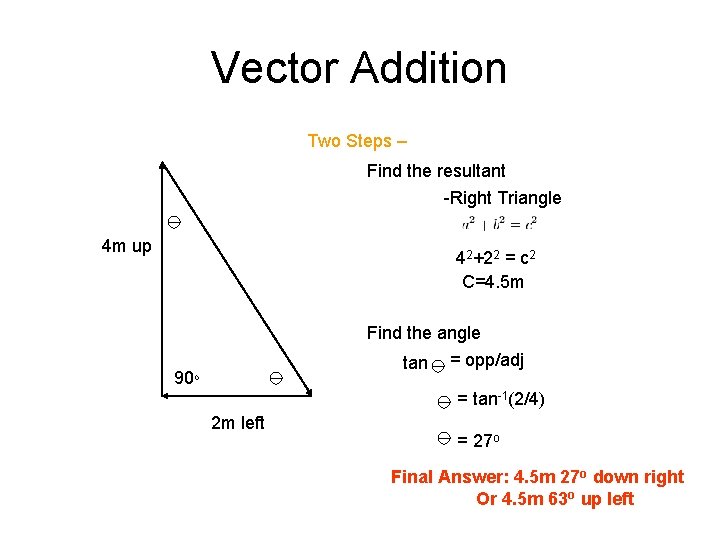
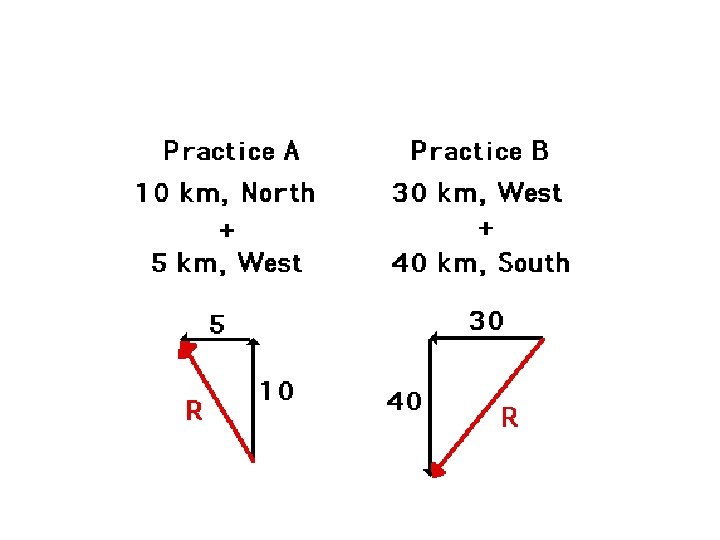
Vector Addition Two Steps – Find the resultant -Right Triangle 4 m up 42+22 = c 2 C=4. 5 m Find the angle tan = opp/adj 90 o = tan-1(2/4) 2 m left = 27 o Final Answer: 4. 5 m 27 o down right Or 4. 5 m 63 o up left

Vector Resolution • Find the x and y components of a given angle and vector (resultant) • Example: Given a vector at 60 o with a magnitude 50 m/s. Find the x and y velocities 1. Set scale. 2. Use trig. functions. • Find vy with sin and vx with cos • Vy=sin(60 o)*50 m/s • Vx =cos(60 o)*50 m/s

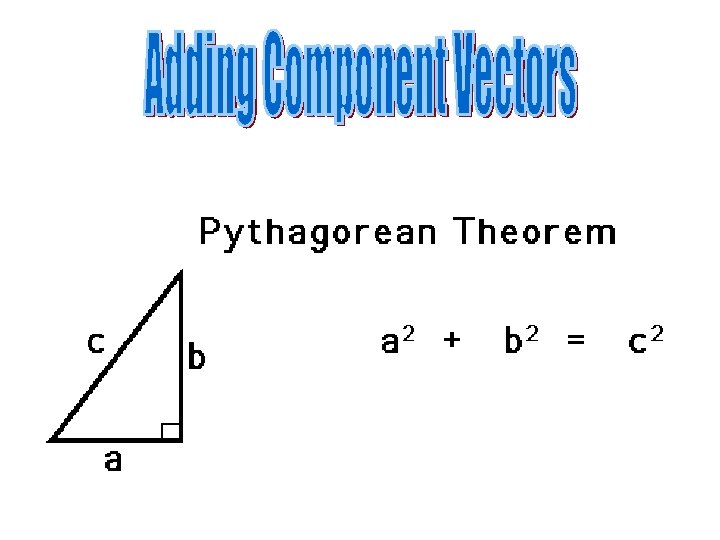
Summary • Finding Magnitude of Vector (addition) – Parallel vectors: add (same direction) or subtract (opposite directions) – Perpendicular (900) – Pythagorean theorem. • Finding Magnitude of Components (resolution) – Given angle and resultant – use trig functions to find x and y components

Relative Velocity We already considered relative speed in one dimension; it is similar in two dimensions except that we must add and subtract velocities as vectors. Each velocity is labeled first with the object, and second with the reference frame in which it has this velocity. Therefore, v. WS is the velocity of the water in the shore frame, v. BS is the velocity of the boat in the shore frame, and v. BW is the velocity of the boat in the water frame.

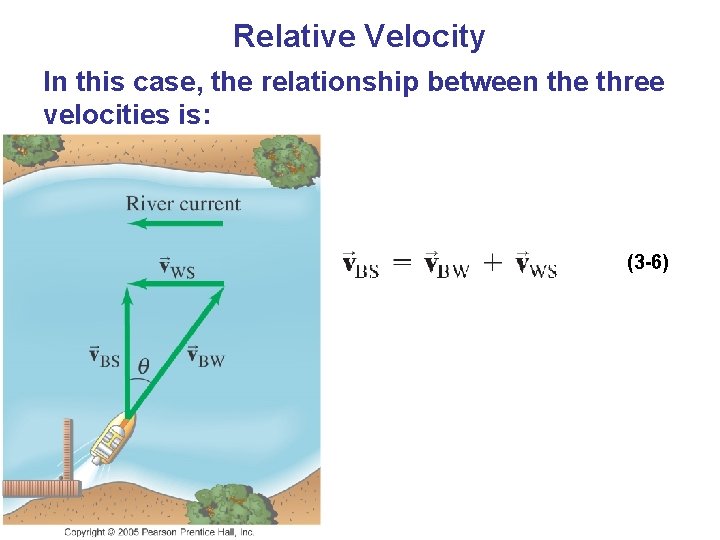
Relative Velocity In this case, the relationship between the three velocities is: (3 -6)

Relative Velocity

Relative Velocity-Sample Problem • A boat is capable of traveling at 5 m/s in still water. The boat attempts to cross a river which runs at 3 m/s downstream. What is the boats velocity as it crosses the river? 5 m/s R 3 m/s

Relative Velocity-Sample Problem Answer: 5. 83 m/s at 30. 96 o downstream

Relative Velocity-Sample Problem • If the river is 1 km wide, how long will it take the boat to cross the river? This problem turns into a simple linear motion problem. The boat has a velocity across the river of 5 m/s and the distance straight across the river is 1 km.

Relative Velocity-Sample Problem Answer: 200 seconds

Relative Velocity-Sample Problem • How far downstream does the boat end up? This also turns into a simple linear motion problem. Your boat is moving downstream at 3 m/s and it is in the water for 200 seconds.

Relative Velocity-Sample Problem Answer: 600 m

Relative Velocity-Sample Problem • A railway car is moving at 2 m/s and a man starts to walk from the back of the car to the front at 1 m/s. What is his velocity relative to the ground? Answer: 3 m/s

An airplane flies at an engine speed of 100 m/s at 50º W of S into a wind of 30 m/s at 200 E of N. What is the airplane’s resultant velocity? Solve using the components method!! How far has the plane traveled after 1 hr? ? Answer: 75. 52 m/s @ 28. 54˚ S of W 168. 89 miles per 1 hour

You Try!!! A motor boat traveling 4. 0 m/s, East encounters a current traveling 3. 0 m/s, North. a. What is the resultant velocity of the motor boat? b. If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore? c. What distance downstream does the boat reach the opposite shore?