Physics Vector Resolution Force Components In what direction

Physics Vector Resolution Force Components

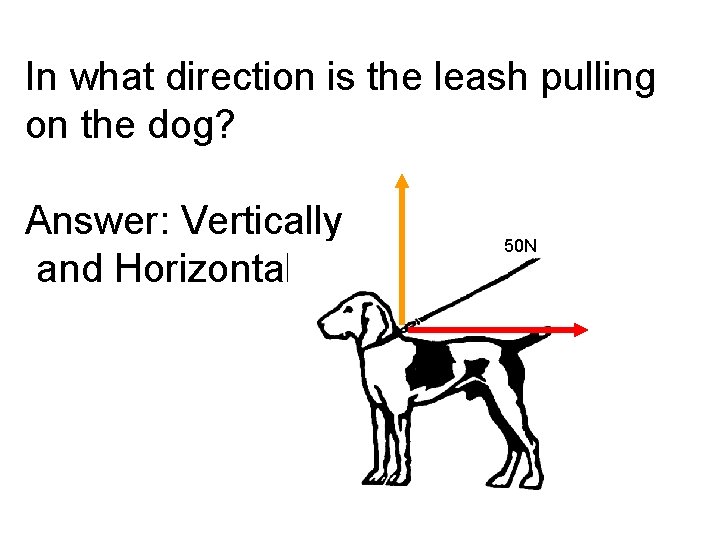
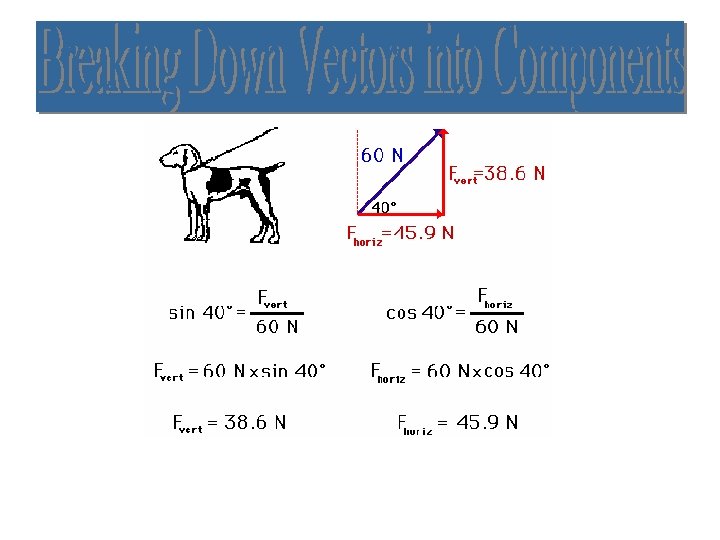
In what direction is the leash pulling on the dog? Answer: Vertically and Horizontally 50 N

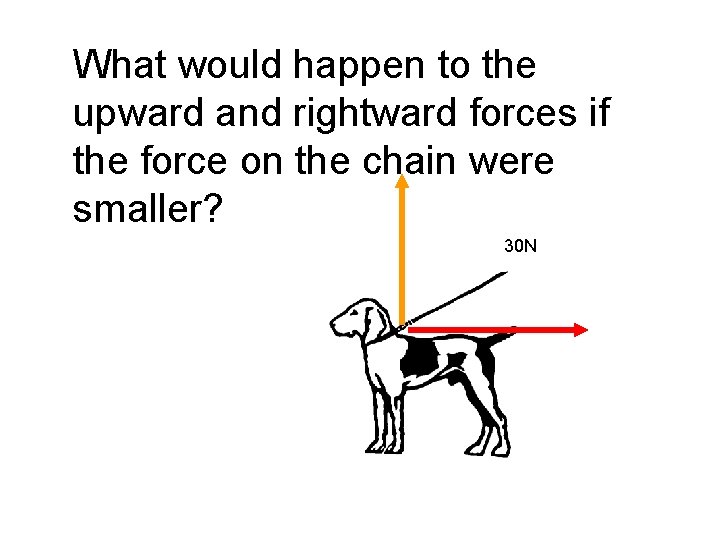
What would happen to the upward and rightward forces if the force on the chain were smaller? 30 N

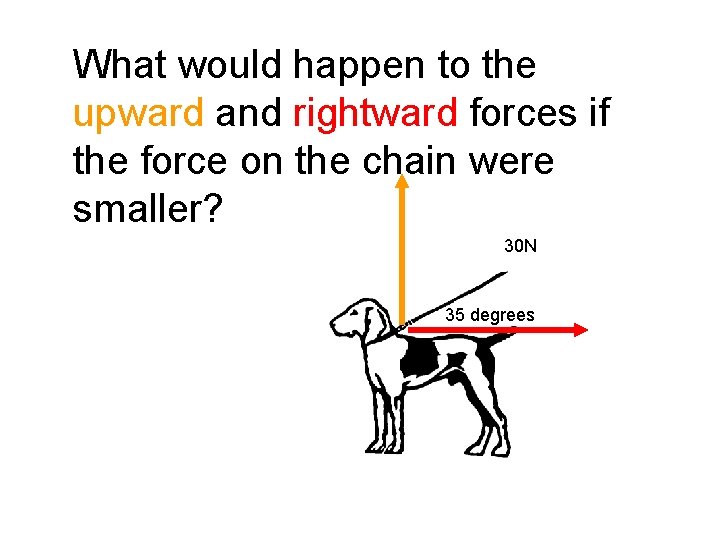
What would happen to the upward and rightward forces if the force on the chain were smaller? 30 N 35 degrees

What would happen to the upward and rightward forces if the angle on the chain were smaller?

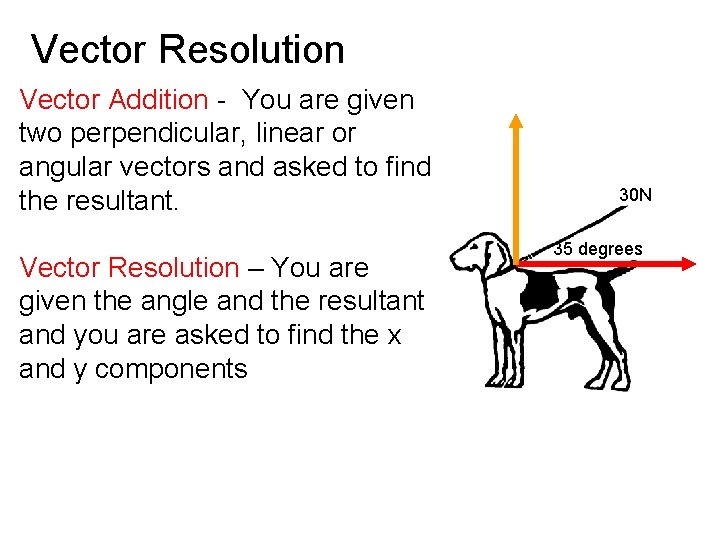
Vector Resolution Vector Addition - You are given two perpendicular, linear or angular vectors and asked to find the resultant. Vector Resolution – You are given the angle and the resultant and you are asked to find the x and y components 30 N 35 degrees

Adding Vectors by Components Adding vectors: 1. Draw a diagram; add the vectors graphically. 2. Choose x and y axes. 3. Resolve each vector into x and y components. 4. Calculate each component using sines and cosines. 5. Add the components in each direction. 6. To find the length and direction of the vector, use:

1) Find the resultant Magnitude: _____ 24. 99 N 34. 90º N of W of the two vectors. Direction: ______ Vector #1 = 20. 5 N West Vector #2 = 14. 3 N North Vector Diagram V 2 VR=? V 1

2) Find the component of the resultant = 255 m 27º South of East 115. 8 m Direction_____ South (-) Vector # 1 _______ East (+) 227. 2 m Direction_____ Vector # 2____ Vector Diagram: Conventions: V 2 Vr + V 1 - + -

Skip Practice: Find FR = Fnet =? 200 N due South, Draw vector diagram. (Draw axis)100 N at 40º N of W 1. 2. Resolve vectors into components using trig: Vadj = V cos θ Vopp = V sin θ 3. Sum x and y components: ΣVxi ΣVyi 4. Redraw!! Determine resultant vector using Pythagorean’s Theorem and trig: Answer: Fnet = N @ ˚ W of S Magnitude= √(Σ Vxi)² + (Σ Vyi)² Direction Action: θ = tan-1(opp/adj)

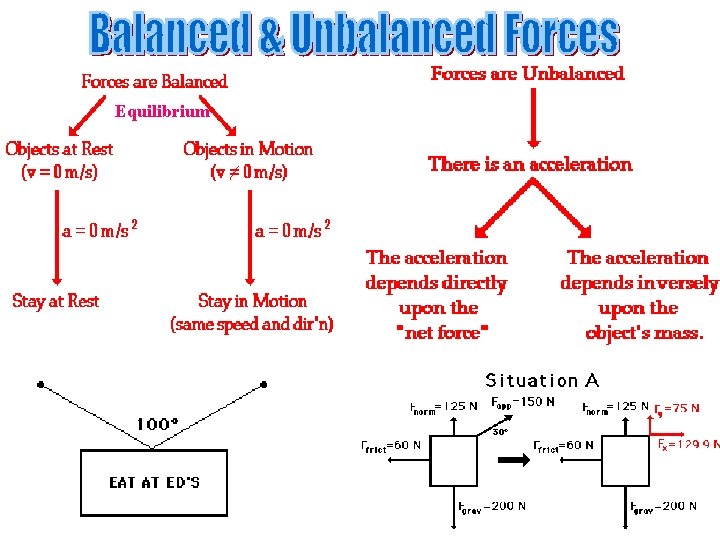
Net Force – Summing Forces

Equilibrium

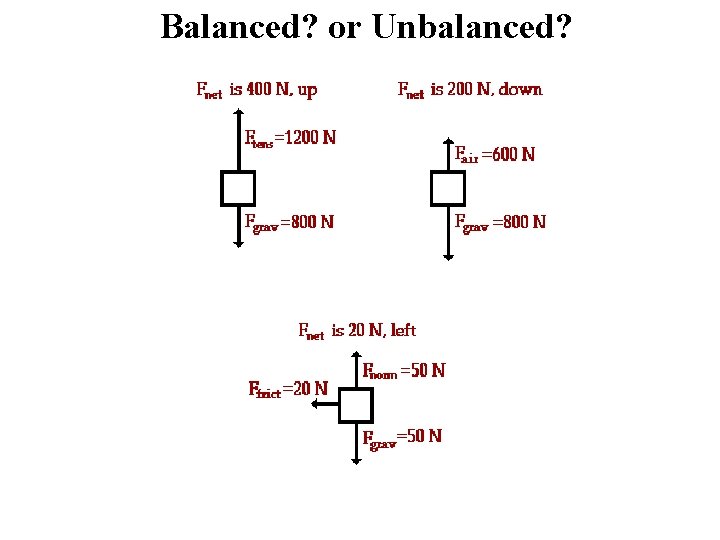
Balanced? or Unbalanced?

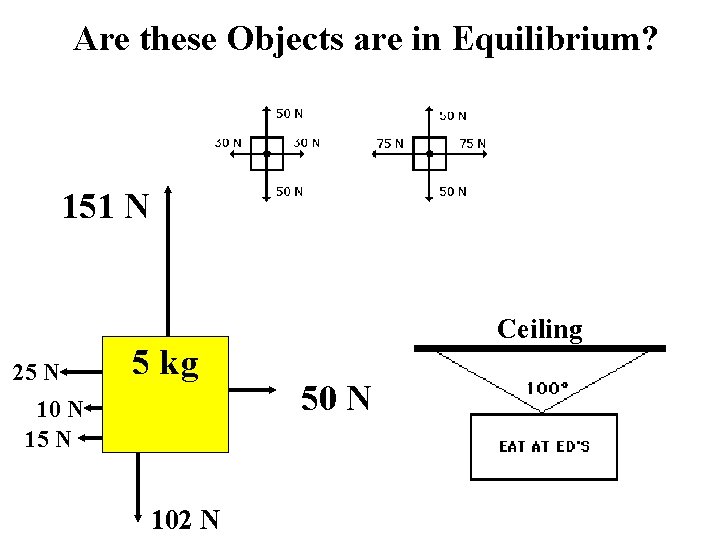
Are these Objects are in Equilibrium? 151 N 25 N 5 kg 10 N 15 N 102 N Ceiling 50 N

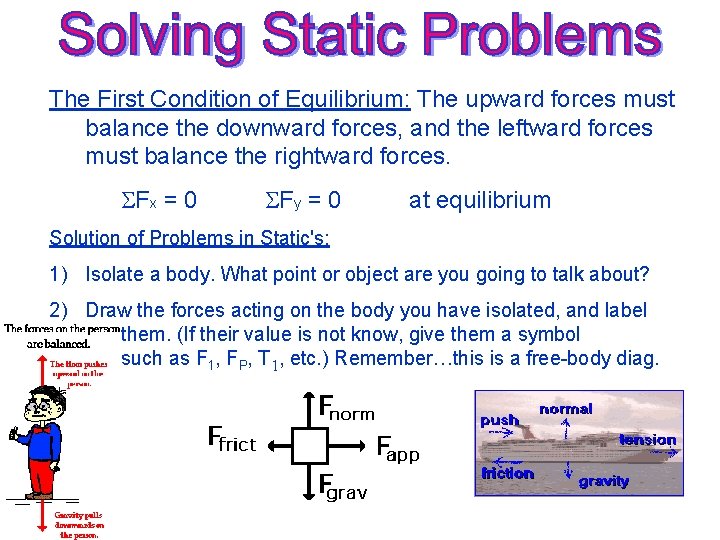
The First Condition of Equilibrium: The upward forces must balance the downward forces, and the leftward forces must balance the rightward forces. SFx = 0 SFy = 0 at equilibrium Solution of Problems in Static's: 1) Isolate a body. What point or object are you going to talk about? 2) Draw the forces acting on the body you have isolated, and label them. (If their value is not know, give them a symbol such as F 1, FP, T 1, etc. ) Remember…this is a free-body diag.

Cont. 3) Split each of the forces into its x and y components, and label the components in terms of the symbols given in rule 2 and the proper sines and cosines. 4) 4) Write down your summation equations for the first condition of equilibrium. 5) 5) Solve the equations for the unknowns.

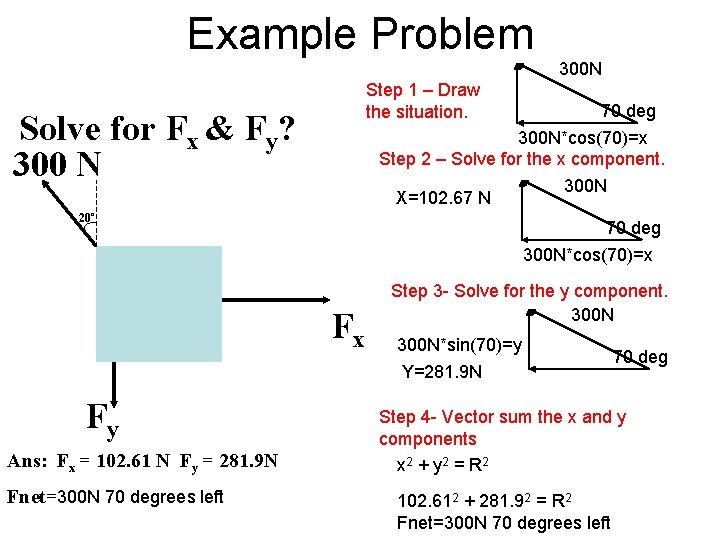
Example Problem 300 N Step 1 – Draw the situation. Solve for Fx & Fy? 300 N 70 deg 300 N*cos(70)=x Step 2 – Solve for the x component. 300 N X=102. 67 N 20º 70 deg 300 N*cos(70)=x Fx Fy Ans: Fx = 102. 61 N Fy = 281. 9 N Fnet=300 N 70 degrees left Step 3 - Solve for the y component. 300 N*sin(70)=y Y=281. 9 N 70 deg Step 4 - Vector sum the x and y components x 2 + y 2 = R 2 102. 612 + 281. 92 = R 2 Fnet=300 N 70 degrees left

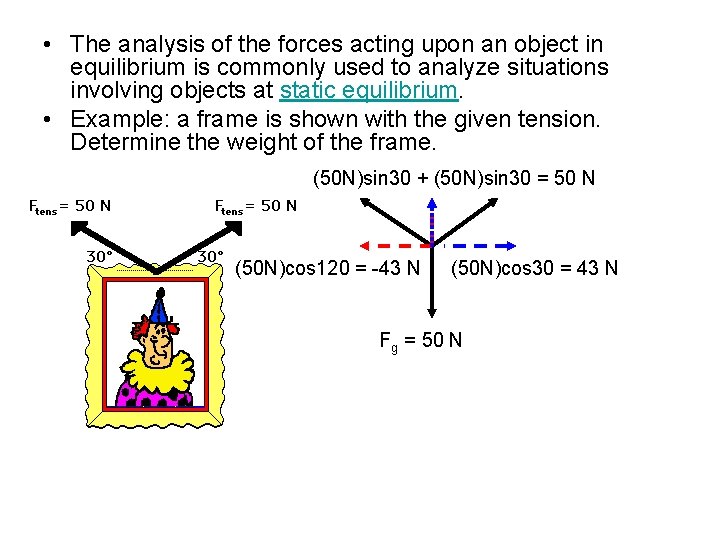
• The analysis of the forces acting upon an object in equilibrium is commonly used to analyze situations involving objects at static equilibrium. • Example: a frame is shown with the given tension. Determine the weight of the frame. (50 N)sin 30 + (50 N)sin 30 = 50 N (50 N)cos 120 = -43 N (50 N)cos 30 = 43 N Fg = 50 N

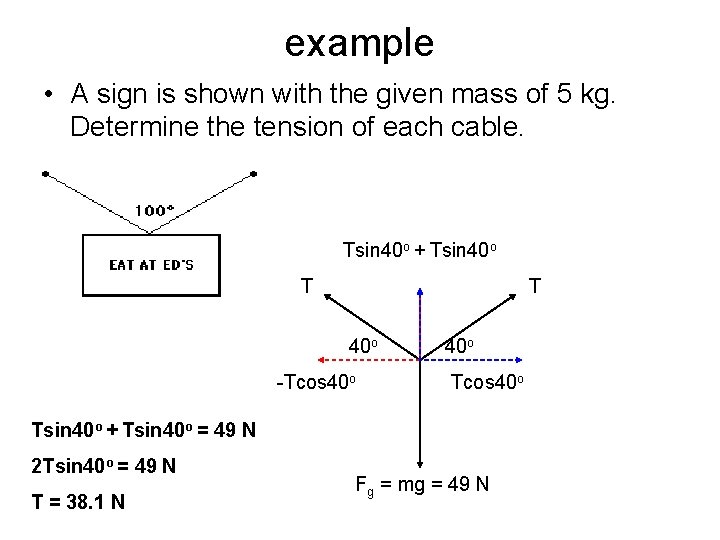
example • A sign is shown with the given mass of 5 kg. Determine the tension of each cable. Tsin 40 o + Tsin 40 o T T 40 o -Tcos 40 o Tsin 40 o + Tsin 40 o = 49 N 2 Tsin 40 o = 49 N T = 38. 1 N Fg = mg = 49 N

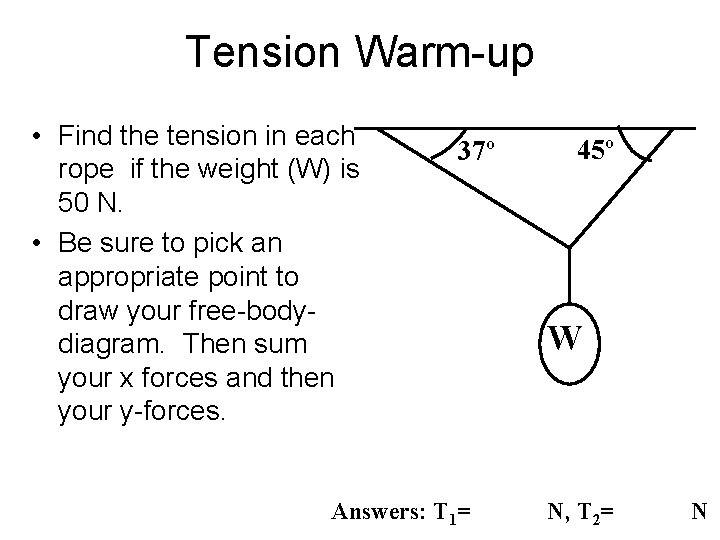
Tension Warm-up • Find the tension in each rope if the weight (W) is 50 N. • Be sure to pick an appropriate point to draw your free-bodydiagram. Then sum your x forces and then your y-forces. 37º Answers: T 1= 45º W N, T 2= N