Physics of the Trampoline Effect baseball golf tennis

Physics of the Trampoline Effect baseball, golf, tennis, . . . Alan M. Nathana, Daniel Russellb, Lloyd Smithc a. University of Illinois at Urbana-Champaign b. Kettering University c. Washington State University

The “Trampoline” Effect: A Simple Physical Picture • Two springs mutually compress each other – KE PE KE • PE shared between “ball spring” and “bat spring” – PE stored in ball mostly dissipated – PE stored in bat mostly restored • Net effect: less overall energy dissipated – e e 0: the trampoline effect • e 0 COR for ball on rigid surface – 1 -e 02 = fraction of ball PE dissipated • e COR for ball on flexible surface – 1 -e 2 = fraction of initial ball KE lost to ball

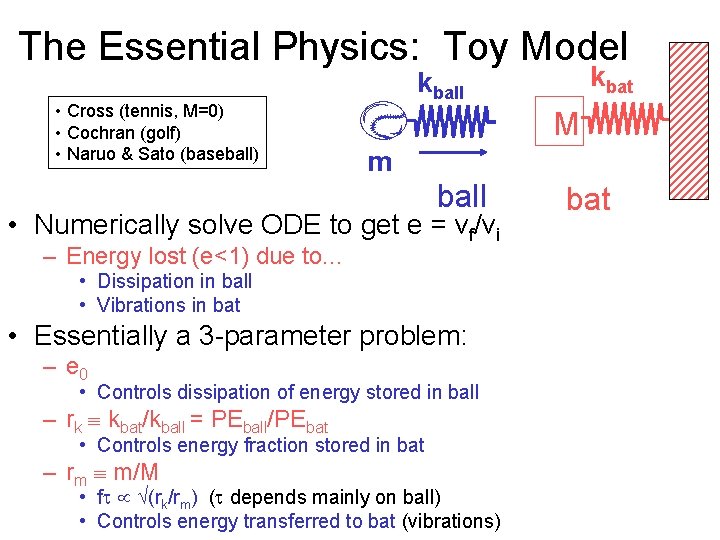
The Essential Physics: Toy Model • Cross (tennis, M=0) • Cochran (golf) • Naruo & Sato (baseball) M m ball • Numerically solve ODE to get e = vf/vi – Energy lost (e<1) due to. . . • Dissipation in ball • Vibrations in bat • Essentially a 3 -parameter problem: – e 0 • Controls dissipation of energy stored in ball – rk kbat/kball = PEball/PEbat • Controls energy fraction stored in bat – rm m/M kbat kball • f (rk/rm) ( depends mainly on ball) • Controls energy transferred to bat (vibrations) bat

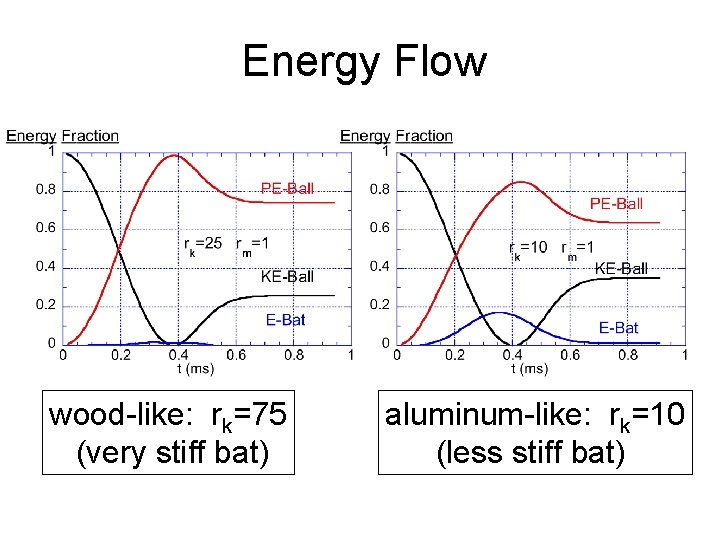
Energy Flow wood-like: rk=75 (very stiff bat) aluminum-like: rk=10 (less stiff bat)

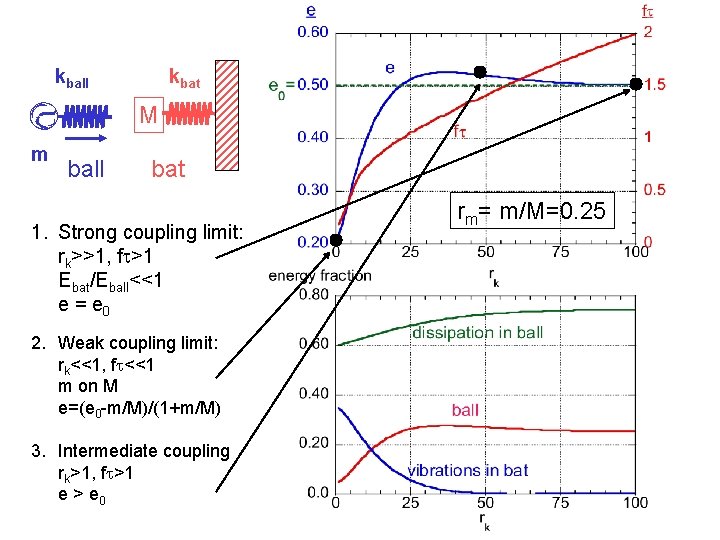
kball kbat M m ball bat 1. Strong coupling limit: rk>>1, f >1 Ebat/Eball<<1 e = e 0 2. Weak coupling limit: rk<<1, f <<1 m on M e=(e 0 -m/M)/(1+m/M) 3. Intermediate coupling rk>1, f >1 e > e 0 rm= m/M=0. 25

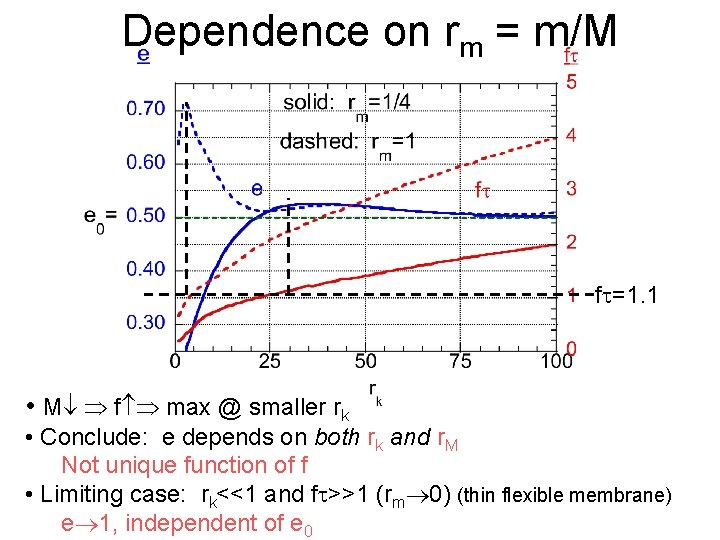
Dependence on rm = m/M f =1. 1 • M f max @ smaller rk • Conclude: e depends on both rk and r. M Not unique function of f • Limiting case: rk<<1 and f >>1 (rm 0) (thin flexible membrane) e 1, independent of e 0

Important Results (all confirmed experimentally) • Harder ball or softer bat decreases rk, increases e • Nonlinear baseball: kball increases with vi e/e 0 increases with vi • e/e 0 (“BPF”) decreases as e 0 increases • Collision time increases as rk decreases USGA pendulum test

Realizing the Trampoline Effect in Baseball/Softball Bats Bending Modes kbat R 4: large in barrel little energy stored vs. Hoop Modes kbat (t/R)3: small in barrel more energy stored f (170 Hz, etc) < 1 f (1 -2 k. Hz) > 1 stored energy vibrations energy mostly restored Net effect: e e 0 on sweet spot Net Effect: e<<e 0 off sweet spot e/e 0 = 1. 20 -1. 35 no trampoline effect

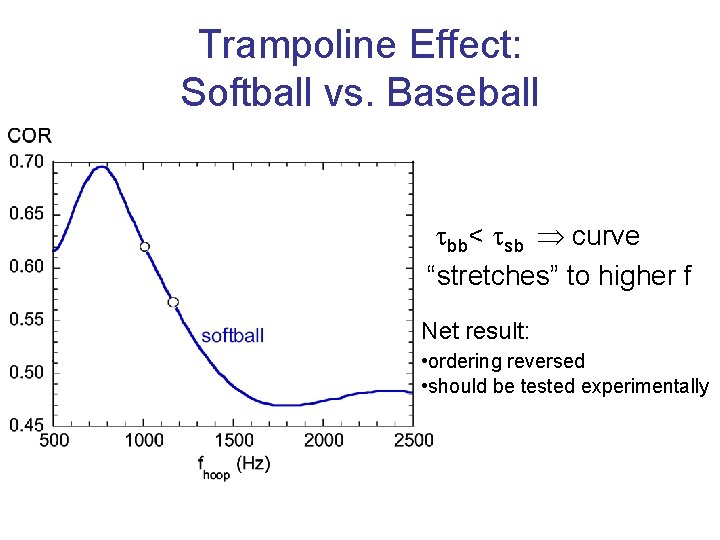
Trampoline Effect: Softball vs. Baseball bb< sb curve “stretches” to higher f Net result: • ordering reversed • should be tested experimentally

Summary • Simple physical model developed for trampoline effect • Model qualitatively accounts for observed phenomena with baseball/softball bats – Both rk and r. M are important – e/e 0 not a bat property independent of e 0 • Relative performance of bats depends on the ball! – But this needs to be tested