Physics of Quark Hadron Phase Transition Michal umbera

Physics of Quark Hadron Phase Transition Michal Šumbera ÚJF AV ČR

Prologue “if we look back to the first 0. 0001 second of cosmic history when temperature was above 1012 K we encounter theoretical problems of a difficulty beyond the range of modern statistical mechanics. At such temperatures there will be a large number of strongly interacting particles in thermal equilibrium - mesons, baryons and antibaryons – with average interparticle distances smaller than typical Compton wavelenght. Particles will be in state of perpetual interaction and there is 1012 no K 100 Me. V
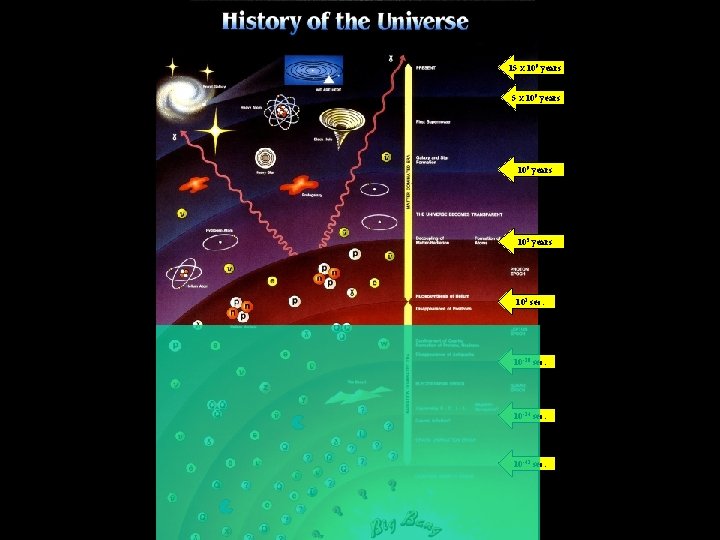
15 x 109 years 105 years 102 sec. 10 -10 sec. 10 -34 sec. 10 -43 sec.
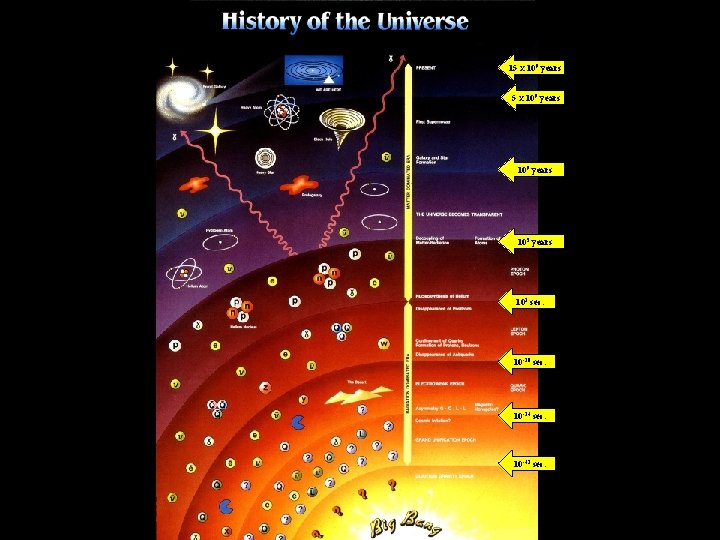
15 x 109 years 105 years 102 sec. 10 -10 sec. 10 -34 sec. 10 -43 sec.
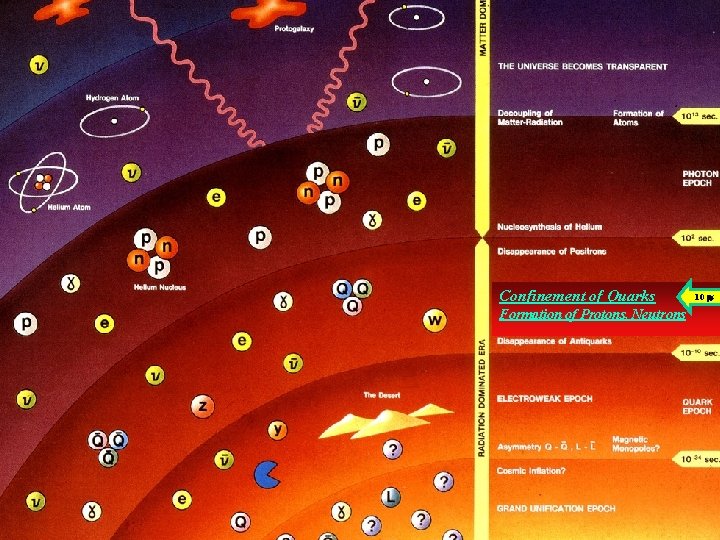
Confinement of Quarks Formation of Protons, Neutrons 10 s

• 1973 = Birth of QCD • The discovery of “asymptotic freedom” • Gross, Politzer, Wilczek
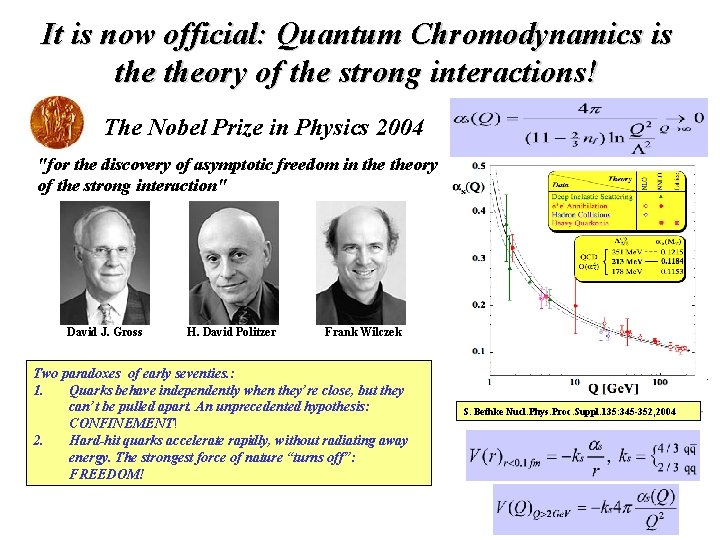
It is now official: Quantum Chromodynamics is theory of the strong interactions! The Nobel Prize in Physics 2004 "for the discovery of asymptotic freedom in theory of the strong interaction" David J. Gross H. David Politzer Frank Wilczek Two paradoxes of early seventies. : 1. Quarks behave independently when they’re close, but they can’t be pulled apart. An unprecedented hypothesis: CONFINEMENT! 2. Hard-hit quarks accelerate rapidly, without radiating away energy. The strongest force of nature “turns off”: FREEDOM! S. Bethke Nucl. Phys. Proc. Suppl. 135: 345 -352, 2004
x rado a P m : Fro W m k o n d a 4 e Fr , 200 c Fre i 8 t r o e t b mp ecem “Asy D , e r Lectu 3 l e b 0211 5 No 0 / h p hep: v i Ar. X k: ilcze m radig a P to ”

Brief history of Quark-Gluon Plasma 1974: T. D. Lee suggested „vacuum engineering“ strategy to temporarily restore broken symmetries of the physical vacuum and possibly create novel abnormal dense states of nuclear matter. 1975: W. Greiner and collaborators pointed out that the required high densities could be achieved via relativistic heavy ion collisions. 1975: J. C. Collins & M. J. Perry realized that the asymptotic freedom property of QCD implies the existence of an ultradense form of matter with deconfined quarks and gluons. 1975: N. Cabibo & G. Parisi suggested that exponentialy increasing spectrum of hadronic states indicates existence of deconfined quark phase at temperature T m. 1978: E. V. Shuryak introduced term quark–gluon plasma to describe this novel form of matter. J. Kapusta, B. Müller & J. Rafelski: Quark-Gluon Plasma, Theoretical Foundations, An annotated reprint collection, Elsevier 2003

Importance of the Quark Gluon Plasma 1. It is the ultimate, primordial form of QCD matter at high temperature or baryon number density. 2. It was present during the first few microseconds of the Big Bang. 3. It provides an example of phase transitions which may occur at a variety of higher temperature scales in the early universe. 1. It can provide important insights on the origin of mass for matter, and how quarks are confined into hadrons.

1. Introducing QCD Matter

Festschrift in honor of B. L. Ioffe, ”At the Frontier of Particle Physics / Handbook of QCD”, M. Shifman, ed. , (World Scientific).
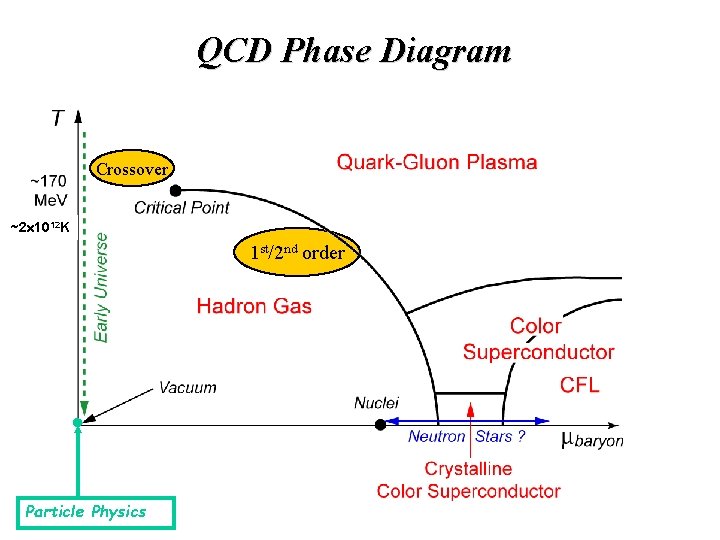
QCD Phase Diagram Crossover ~2 1012 K 1 st/2 nd order Particle Physics

High Temperature QCD Phase Transition in a Nutshell Q: How to liberate quarks and gluons from ~1 fm confinement scale? A: Create an energy density >> normal nuclear density: Rough Estimate: Ideal gas of massles non-interacting particles) Energy density for “g” massless d. o. f 8 gluons, 2 spins; 2 quark flavors, anti-quarks, 2 spins, 3 colors 4. 3 x 1015 g/cm 3

High Temperature QCD Phase Transition in a Nutshell Q: How to liberate quarks and gluons from ~1 fm confinement scale? A: Create an energy density >> normal nuclear density: Rough Estimate: Ideal gas of massles non-interacting particles) Energy density for “g” massless d. o. f 8 gluons, 2 spins; 3 quark flavors, anti-quarks, 2 spins, 3 colors 5. 4 x 1015 g/cm 3
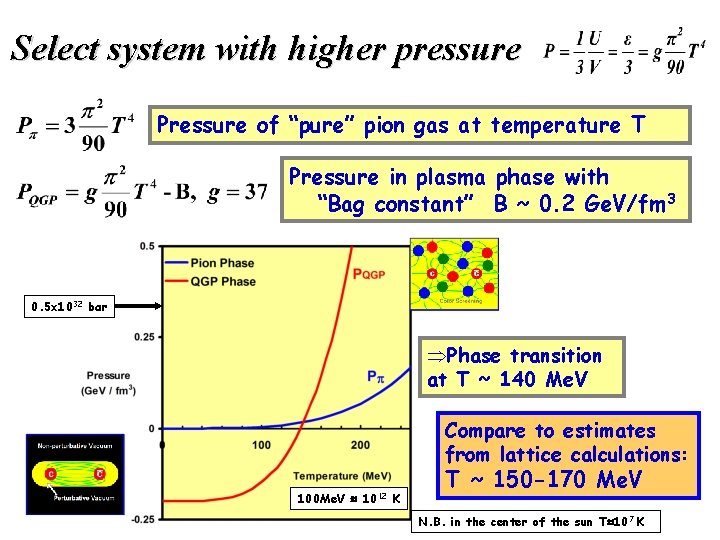
Select system with higher pressure Pressure of “pure” pion gas at temperature T Pressure in plasma phase with “Bag constant” B ~ 0. 2 Ge. V/fm 3 0. 5 x 1032 bar Phase transition at T ~ 140 Me. V Compare to estimates from lattice calculations: 100 Me. V 1012 K T ~ 150 -170 Me. V N. B. in the center of the sun T 107 K

Non-perturbative QCD: L(attice)QCD Solves QCD by numerical evaluation of path integral using a spacetime lattice a V = (Nσ a)3 , T-1 = Nτ a , 10 TFlops QCDOC computing center at BNL N. B. Cost grows as N-7
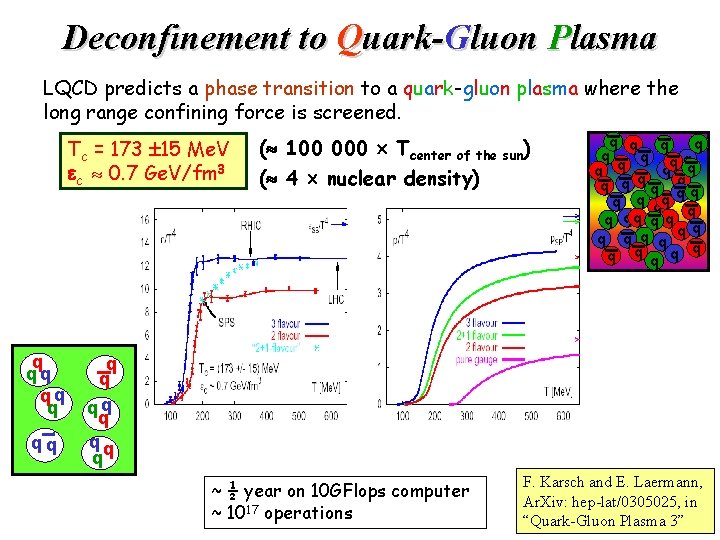
Deconfinement to Quark-Gluon Plasma LQCD predicts a phase transition to a quark-gluon plasma where the long range confining force is screened. Tc = 173 15 Me. V ec 0. 7 Ge. V/fm 3 q qq qq ( 100 000 Tcenter of the sun) ( 4 nuclear density) q q q qq q q q q q qq q ~ ½ year on 10 GFlops computer ~ 1017 operations F. Karsch and E. Laermann, Ar. Xiv: hep-lat/0305025, in “Quark-Gluon Plasma 3”
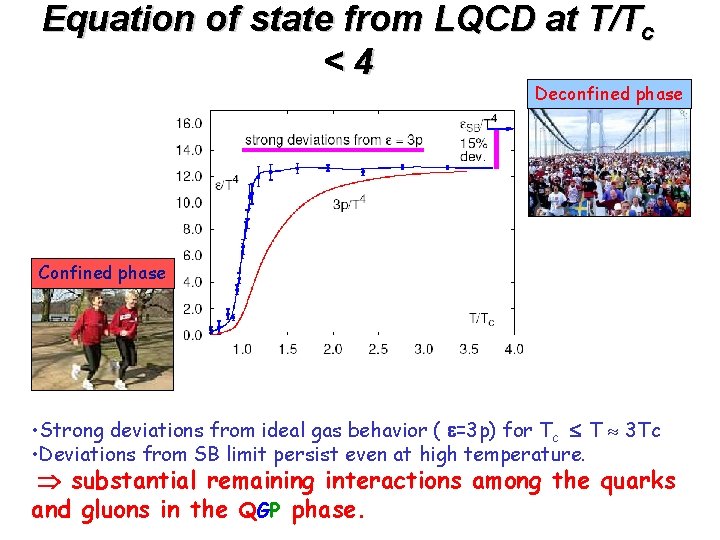
Equation of state from LQCD at T/Tc <4 Deconfined phase Confined phase • Strong deviations from ideal gas behavior ( e=3 p) for Tc T 3 Tc • Deviations from SB limit persist even at high temperature. substantial remaining interactions among the quarks and gluons in the QGP phase.

The plasma Plasma = ionized gas, 99% of visible matter in Universe Different types of plasmas may be generated by high temperatures, electric fields, or radiation Classifications: 1. Non-relativistic – relativistic plasmas 2. Classical – quantum plasmas (white dwarfs) 3. Ideal – strongly coupled plasmas (multi component plasmas containing ions, electrons, neutral gas, and microparticles, e. g. , dust)
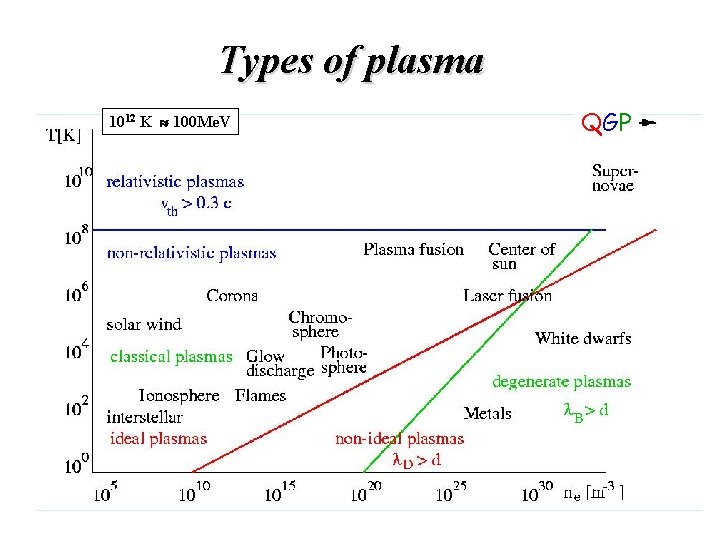
Types of plasma 1012 K 100 Me. V QGP

Strongly Coupled Plasma Coulomb coupling parameter: Q: charge of plasma particles d: inter-particle distance T: plasma temperature Ideal plasmas: G << 1 (most plasmas: G < 10 -3) Strongly coupled plasmas: G > O (1) Example: ion component in white dwarfs Non-perturbative description, e. g. , molecular dynamics One-component plasma, pure Coulomb interaction (repulsive): G > 172 g Coulomb crystal Setsuo Ichimaru: Strongly coupled plasmas: high-density classical plasmas and degenerate electron liquids, Rev. Mod. Phys. 54, 1017–
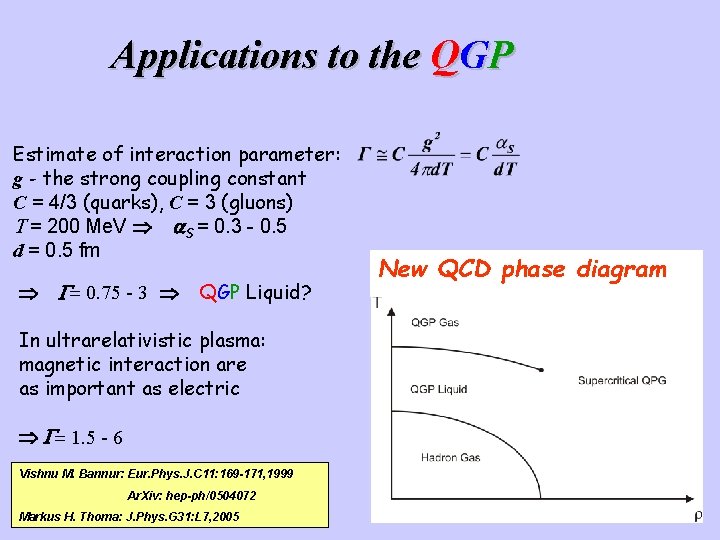
Applications to the QGP Estimate of interaction parameter: g - the strong coupling constant C = 4/3 (quarks), C = 3 (gluons) T = 200 Me. V a. S = 0. 3 - 0. 5 d = 0. 5 fm G= 0. 75 - 3 QGP Liquid? In ultrarelativistic plasma: magnetic interaction are as important as electric G= 1. 5 - 6 Vishnu M. Bannur: Eur. Phys. J. C 11: 169 -171, 1999 Ar. Xiv: hep-ph/0504072 Markus H. Thoma: J. Phys. G 31: L 7, 2005 New QCD phase diagram
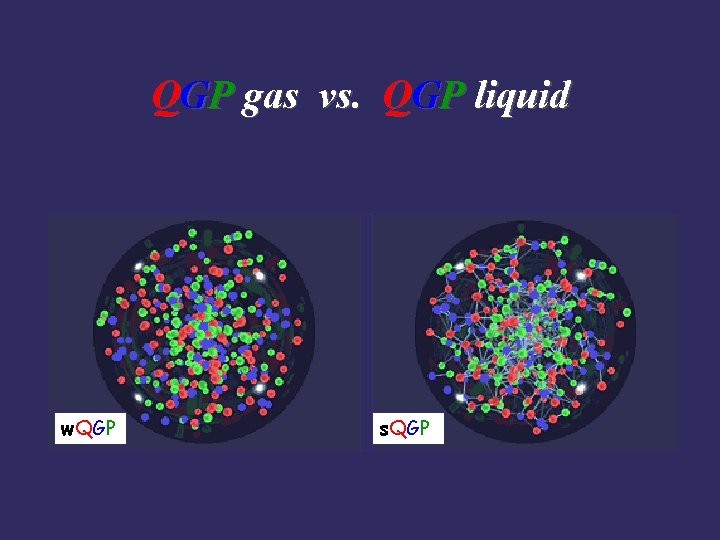
QGP gas vs. QGP liquid w. QGP s. QGP
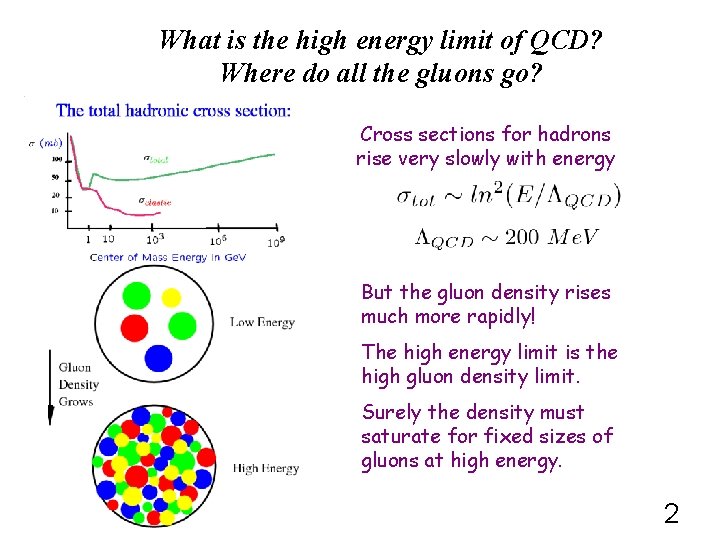
What is the high energy limit of QCD? Where do all the gluons go? Cross sections for hadrons rise very slowly with energy But the gluon density rises much more rapidly! The high energy limit is the high gluon density limit. Surely the density must saturate for fixed sizes of gluons at high energy. 2
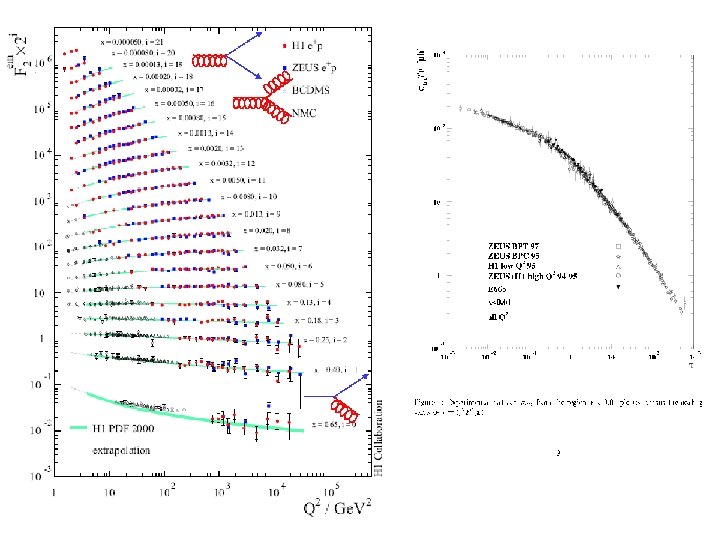

QCD and the classical limit QCD = Quark Model + Gauge Invariance For , . i Classical dynamics applies when the action is large: => Need weak coupling and strong fields
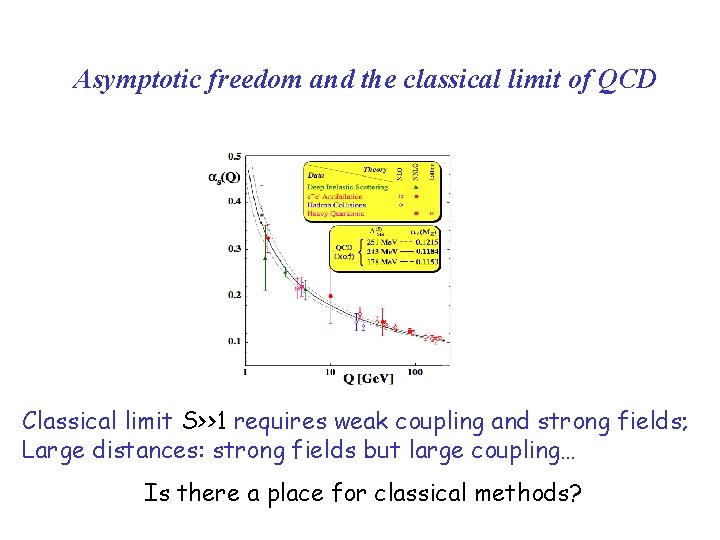
Asymptotic freedom and the classical limit of QCD Classical limit S>>1 requires weak coupling and strong fields; Large distances: strong fields but large coupling… Is there a place for classical methods?

Parton saturation and the classical limit of QCD At small Bjorken x, hard processes develop over. large longitudinal distances All partons contribute coherently at sufficiently small x and/or large A strong fields, weak coupling!
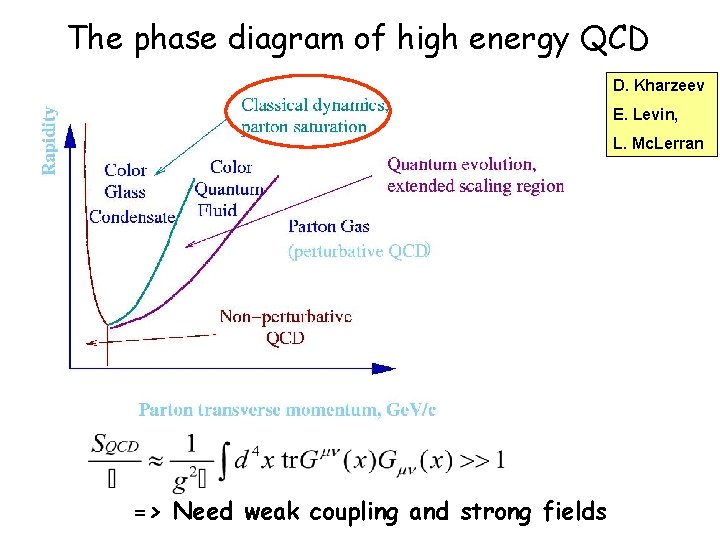
The phase diagram of high energy QCD D. Kharzeev E. Levin, L. Mc. Lerran => Need weak coupling and strong fields

2. From Big-bang to Micro-bang: QCD Phase Transition in the Laboratory
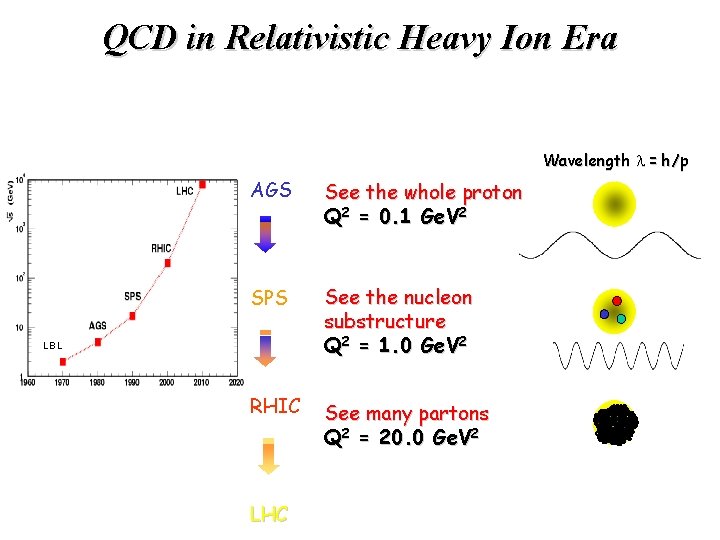
QCD in Relativistic Heavy Ion Era Wavelength l = h/p AGS See the whole proton Q 2 = 0. 1 Ge. V 2 SPS See the nucleon substructure Q 2 = 1. 0 Ge. V 2 RHIC See many partons Q 2 = 20. 0 Ge. V 2 LBL LHC

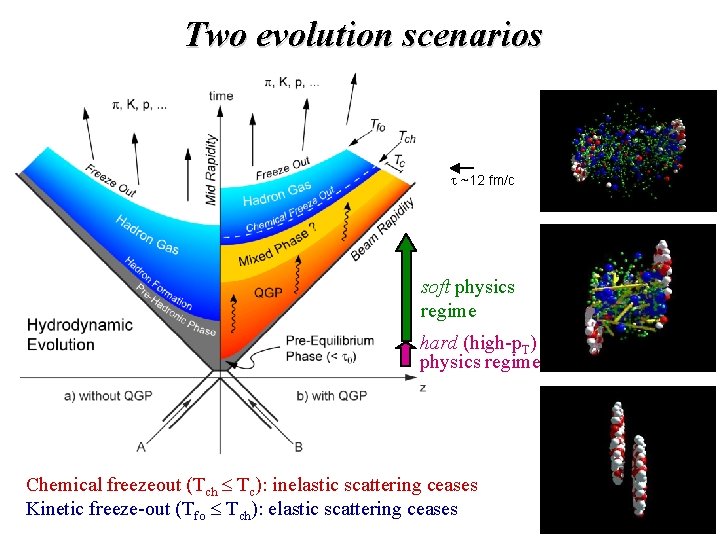
Two evolution scenarios t ~12 fm/c soft physics regime hard (high-p. T) physics regime Chemical freezeout (Tch Tc): inelastic scattering ceases Kinetic freeze-out (Tfo Tch): elastic scattering ceases
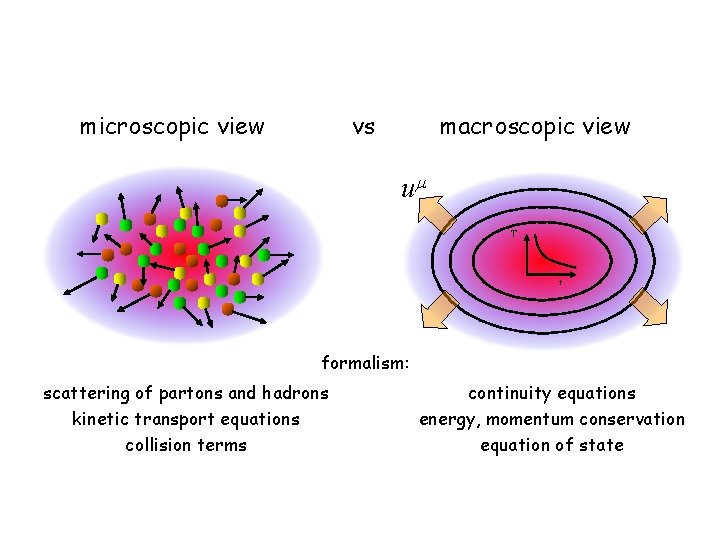
microscopic view vs macroscopic view um T t formalism: scattering of partons and hadrons kinetic transport equations collision terms continuity equations energy, momentum conservation equation of state
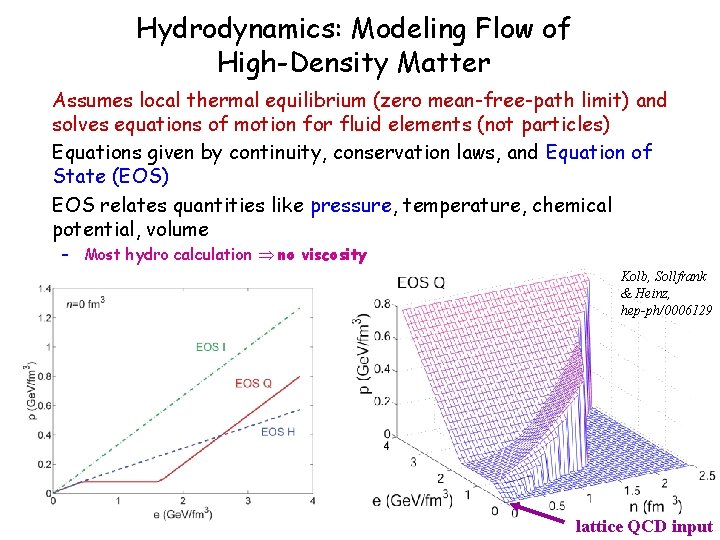
Hydrodynamics: Modeling Flow of High-Density Matter Assumes local thermal equilibrium (zero mean-free-path limit) and solves equations of motion for fluid elements (not particles) Equations given by continuity, conservation laws, and Equation of State (EOS) EOS relates quantities like pressure, temperature, chemical potential, volume – Most hydro calculation no viscosity Kolb, Sollfrank & Heinz, hep-ph/0006129 lattice QCD input
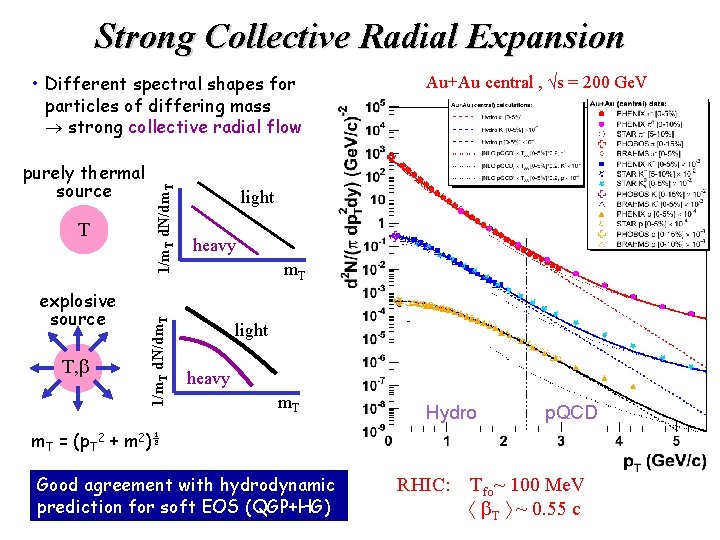
Strong Collective Radial Expansion T explosive source T, b 1/m. T d. N/dm. T purely thermal source 1/m. T d. N/dm. T • Different spectral shapes for particles of differing mass strong collective radial flow Au+Au central , √s = 200 Ge. V light heavy m. T Hydro p. QCD m. T = (p. T 2 + m 2)½ Good agreement with hydrodynamic prediction for soft EOS (QGP+HG) RHIC: Tfo~ 100 Me. V b. T ~ 0. 55 c
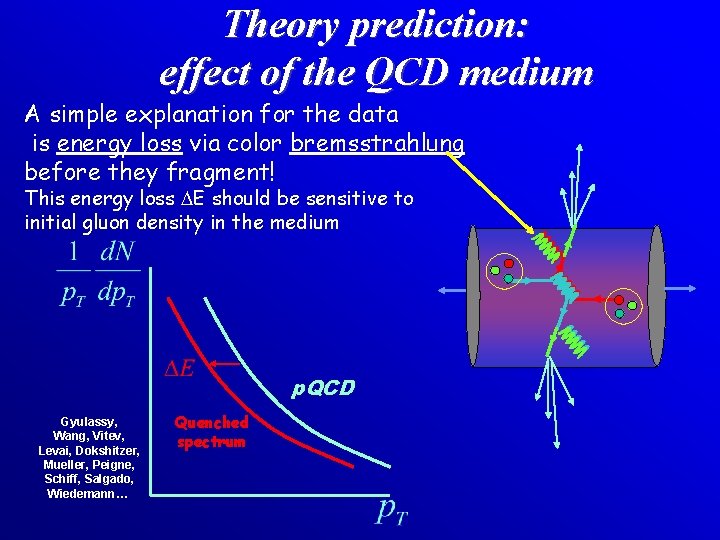
Theory prediction: effect of the QCD medium A simple explanation for the data is energy loss via color bremsstrahlung before they fragment! This energy loss DE should be sensitive to initial gluon density in the medium p. QCD Gyulassy, Wang, Vitev, Levai, Dokshitzer, Mueller, Peigne, Schiff, Salgado, Wiedemann… Quenched spectrum
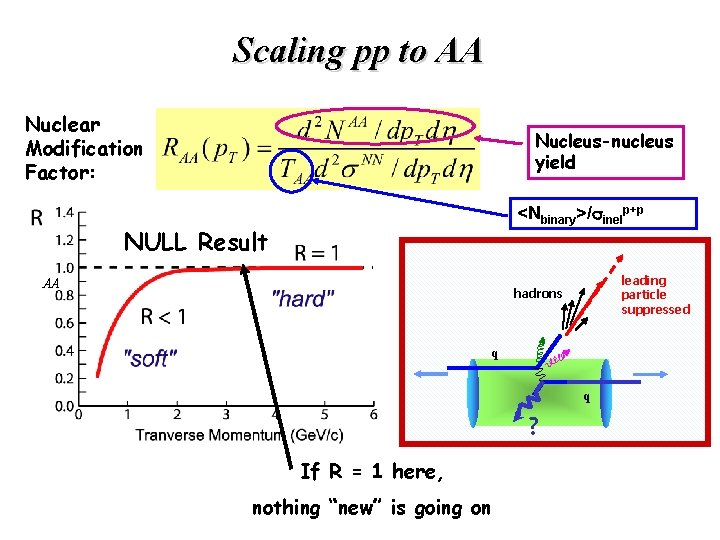
Scaling pp to AA Nuclear Modification Factor: Nucleus-nucleus yield <Nbinary>/sinelp+p NULL Result AA leading particle suppressed hadrons q q ? If R = 1 here, nothing “new” is going on
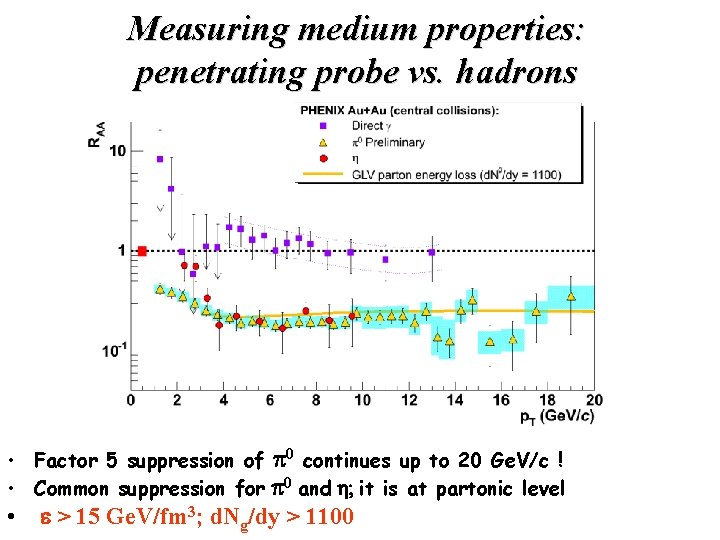
Measuring medium properties: penetrating probe vs. hadrons • Factor 5 suppression of p 0 continues up to 20 Ge. V/c ! • Common suppression for p 0 and h; it is at partonic level • e > 15 Ge. V/fm 3; d. Ng/dy > 1100
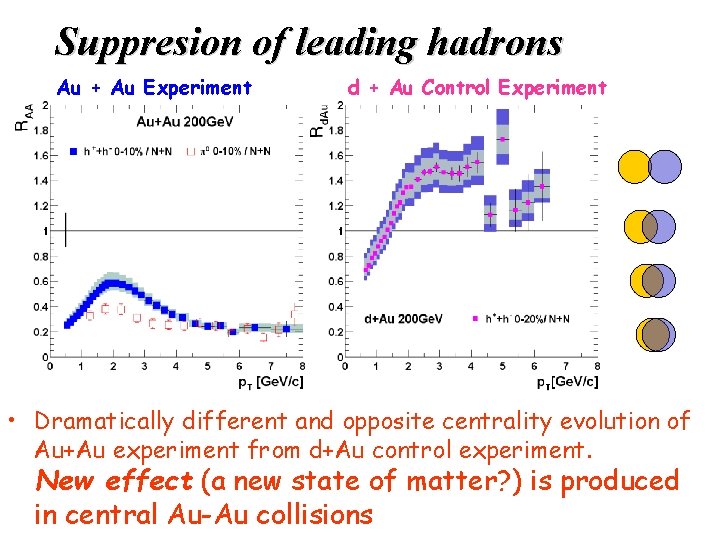
Suppresion of leading hadrons Au + Au Experiment d + Au Control Experiment • Dramatically different and opposite centrality evolution of Au+Au experiment from d+Au control experiment. a New effect (a new state of matter? ) is produced in central Au-Au collisions
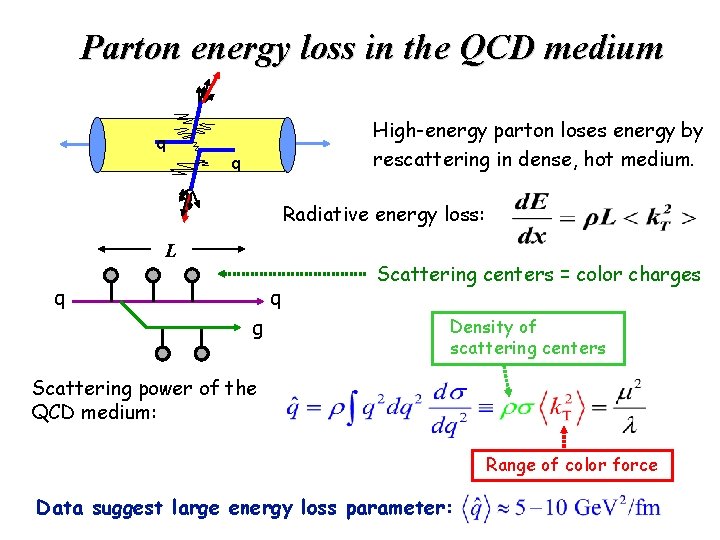
Parton energy loss in the QCD medium High-energy parton loses energy by rescattering in dense, hot medium. q q Radiative energy loss: L q q g Scattering centers = color charges Density of scattering centers Scattering power of the QCD medium: Range of color force Data suggest large energy loss parameter:
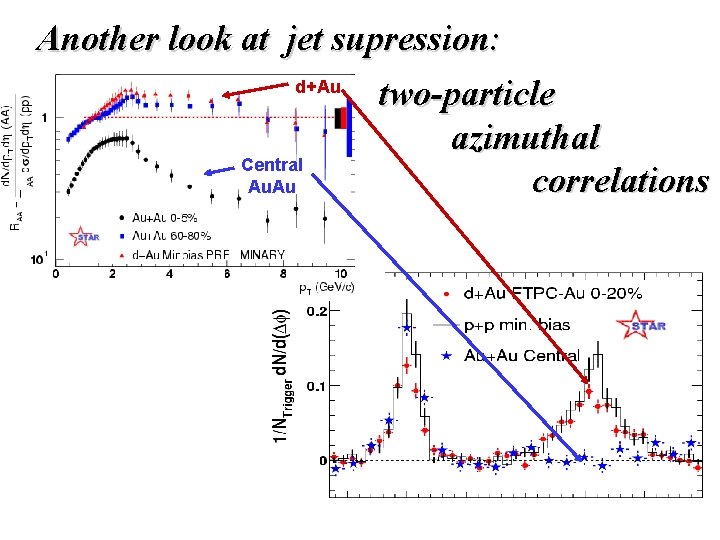
Another look at jet supression: d+Au two-particle azimuthal Central correlations Au. Au Pedestal&flow subtracted 0 90 180 Degrees
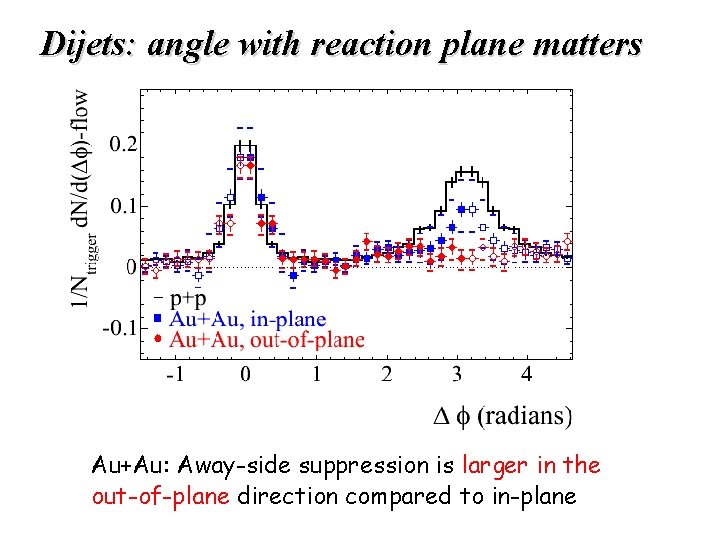
Dijets: angle with reaction plane matters Au+Au: Away-side suppression is larger in the out-of-plane direction compared to in-plane

So is there a QGP at RHIC ? • Experiments & Theory provide overwhelming evidence for new state of matter – – Extreme initial conditions (hydrodynamics, LQCD, p. QCD) Hydrodynamic behavior (collective elliptic & radial flow ) Chemical Equilibrium (particle yields) Jet suppression (opacity, extreme medium density) • This state of matter is not what was originally x expected –no weakly interacting plasma (w. QGP) – no phase transition observed (no latent heat, discontinuities, large fluctuations) • New state of matter seems to be strongly interacting, nearly-perfect fluid (s. QGP) • Currently a cross-over is more likely than a 1 st or 2 nd order phase transition

Epilogue • In 1492 Cristóbal Colón started a long journey with three flag ships - la Nina, la Pinta y la Santa Maria - in the quest for the predicted and expected alternative route to India. • It took quite some time to realize that he had discovered a totally unknown continent (CC actually died in 1506 without knowing it). • In 1986 we started a long journey with 2+1+(1) flag ships - AGS, SPS + RHIC + (LHC) - in the quest for the predicted and expected QGP characterized by free quarks and gluons, deconfinement (J/ ) and chiral symmetry restoration (low-mass dileptons). • Are we discovering our America?

Backup slides

Cross section enhancement in strongly coupled plasmas Reason: Coulomb radius, r. C = Q 2/E, larger than Debye screening length l. D = 1/m. D g modification of Coulomb scattering theory g enhancement of ion-microparticle interaction (ion drag force) QGP : r. C /l. D = 1 – 5 g parton cross section enhancement by factor 2 – 9 g small mean free path l (corresponding to small viscostity h ~ l) and fast thermalization. Implication: - enhancement of collisional energy loss - suppression of radiative energy loss by LPM effect (formation time) g jet quenching
- Slides: 48