Physics of Extra Dimensions A potential discovery for

Physics of Extra Dimensions -A potential discovery for LHC/ILC Abdel Pérez-Lorenzana CINVESTAV PASI-2006, Puerto Vallarta. México.

Program Ø Introduction: Why considering Extra Dimensions? Ø Dimensional reduction: The Effective Field Theory Ø KK decomposition on torii and orbifolds Ø General phenomenological aspects Ø Gravitons Phenomenology Ø Phenomenology of XD matter fields Ø KK modes of Matter Fields: Universal Extra Dimensions Ø New Theoretical ideas for the use of XD

Wonders from the XX century Ø Fundamental interactions are described using two different frameworks: Electroweak and Strong forces in the Standard Model: Gauge Quantum Field Theories SU (3) c ´ SU (2) L ´ U (1) Y with matter in irrep Q (3, 2, 31 ); L (1, 2, -1); e R (1, 1, -2); u R (3, 1, 43 ); d R (3, 1, - 23 ) Symmetry Breaking by Higgs Mechanism Q = T 3 + 21 Y H (1, 2, 1) Hierarchy problem ( : dm H 2 » - l - f + 2 )L 2 Gauge and Flavor Problems… Gravity as Geometry of the Space Time: General Relativity Rmn - 21 g mn R = 8 pc. G 4 N Tmn Not a Quantum Theory (non renormalizable), …. DM, DE, …

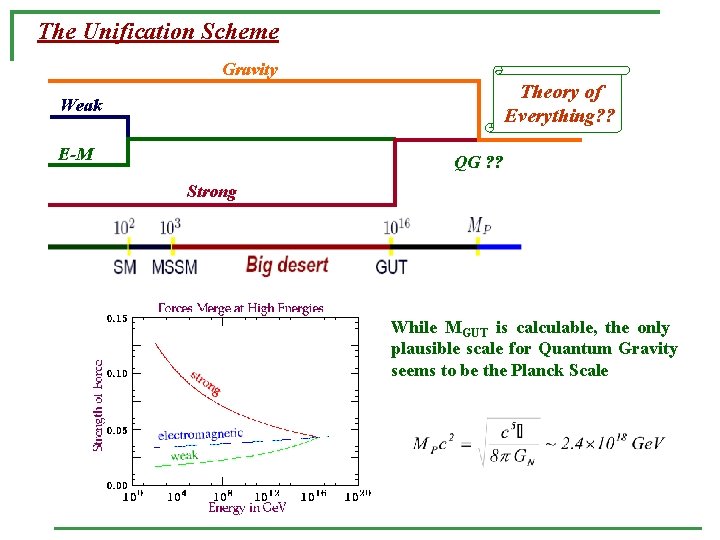
The Unification Scheme Gravity Theory of Everything? ? Weak E-M QG ? ? Strong While MGUT is calculable, the only plausible scale for Quantum Gravity seems to be the Planck Scale

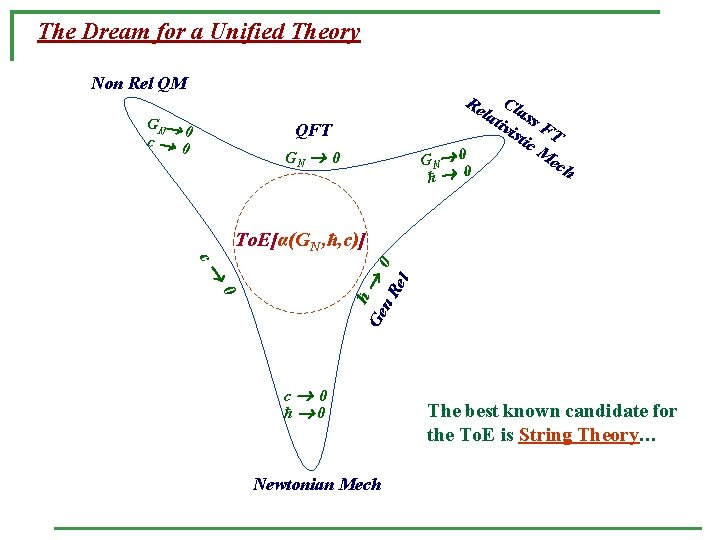
The Dream for a Unified Theory Non Rel QM C lat lass ivi sti FT c. M 0 ec GN Re GN 0 c 0 QFT GN 0 ħ 0 h To. E[α(GN , ħ, c)] 0 ħ Ge n. R 0 el c c 0 ħ 0 Newtonian Mech The best known candidate for the To. E is String Theory…

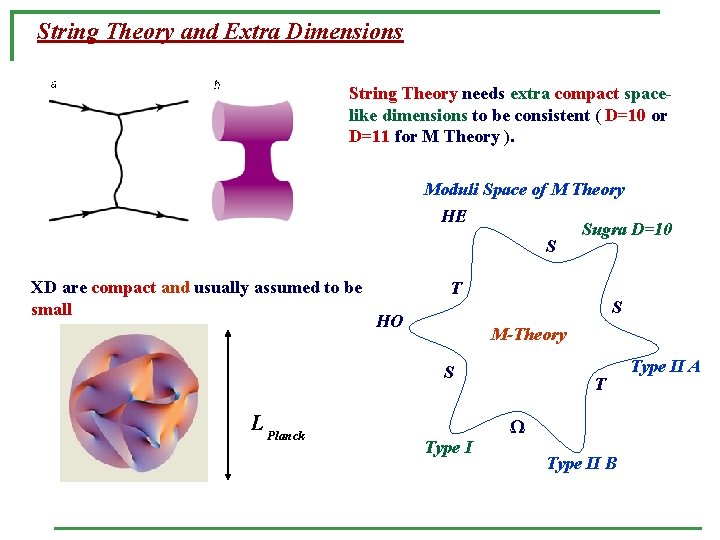
String Theory and Extra Dimensions String Theory needs extra compact spacelike dimensions to be consistent ( D=10 or D=11 for M Theory ). Moduli Space of M Theory HE S XD are compact and usually assumed to be small T HO S M-Theory S L Planck Sugra D=10 Type I T Ω Type II B Type II A

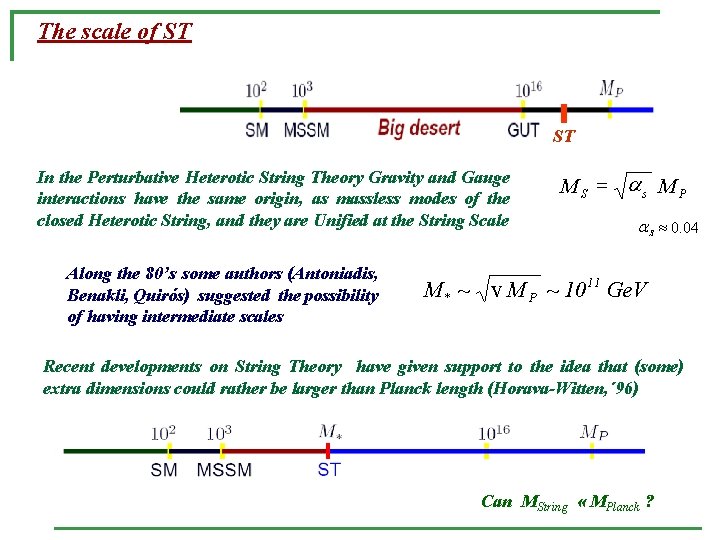
The scale of ST ST In the Perturbative Heterotic String Theory Gravity and Gauge interactions have the same origin, as massless modes of the closed Heterotic String, and they are Unified at the String Scale Along the 80’s some authors (Antoniadis, Benakli, Quirós) suggested the possibility of having intermediate scales M S = as M P a S » 0. 04 M * ~ v M P ~ 10 11 Ge. V Recent developments on String Theory have given support to the idea that (some) extra dimensions could rather be larger than Planck length (Horava-Witten, ´ 96) Can MString « MPlanck ?

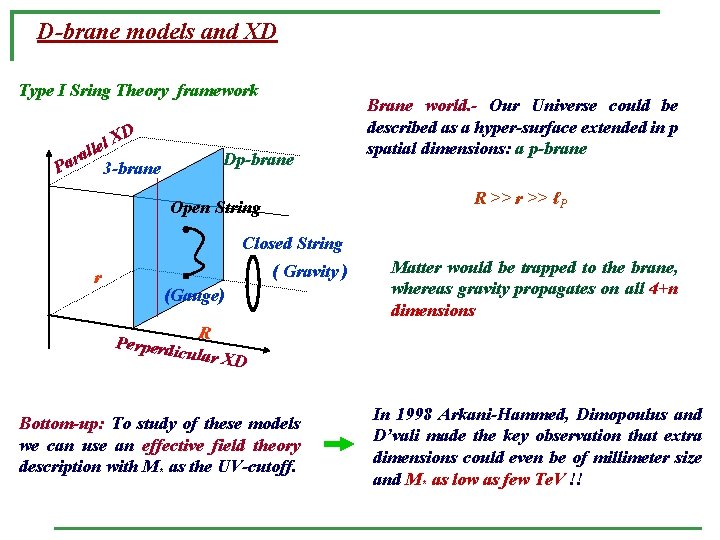
D-brane models and XD Type I Sring Theory framework D X l lle a r 3 -brane Pa Dp-brane Brane world. - Our Universe could be described as a hyper-surface extended in p spatial dimensions: a p-brane R >> r >> ℓP Open String Closed String r ( Gravity ) (Gauge) Perperd Matter would be trapped to the brane, whereas gravity propagates on all 4+n dimensions R icular X D Bottom-up: To study of these models we can use an effective field theory description with M* as the UV-cutoff. In 1998 Arkani-Hammed, Dimopoulus and D’vali made the key observation that extra dimensions could even be of millimeter size and M* as low as few Te. V !!

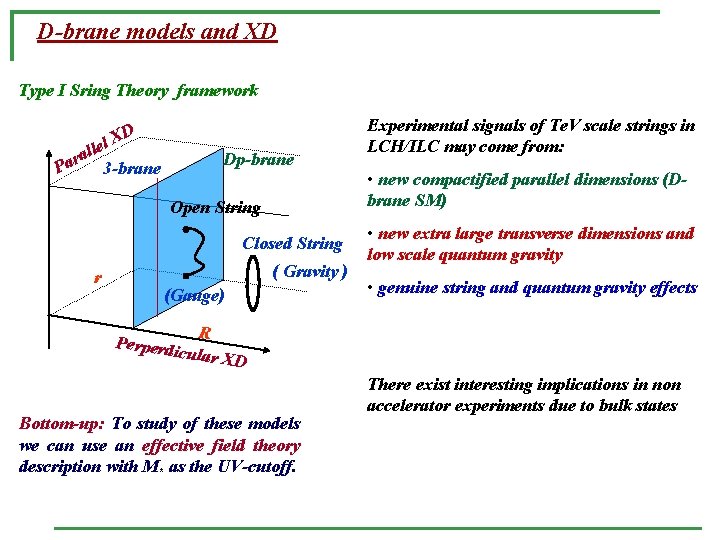
D-brane models and XD Type I Sring Theory framework XD lel l a r 3 -brane Pa Dp-brane Open String Closed String r ( Gravity ) (Gauge) Perperd Experimental signals of Te. V scale strings in LCH/ILC may come from: • new compactified parallel dimensions (Dbrane SM) • new extra large transverse dimensions and low scale quantum gravity • genuine string and quantum gravity effects R icular X D Bottom-up: To study of these models we can use an effective field theory description with M* as the UV-cutoff. There exist interesting implications in non accelerator experiments due to bulk states

MP vs. M* If Einstein gravity theory holds, fundamental gravity coupling does not necessarily coincide with the Newton constant!! vs. The simplest scenario would be considering a flat topology for the extra space, where the bulk is a factorized manifold of the form M 4×T n ADD, 1998 M* ≈ few Te. V ? !! Notice: Vn encodes the actual geometry of the internal manifold.

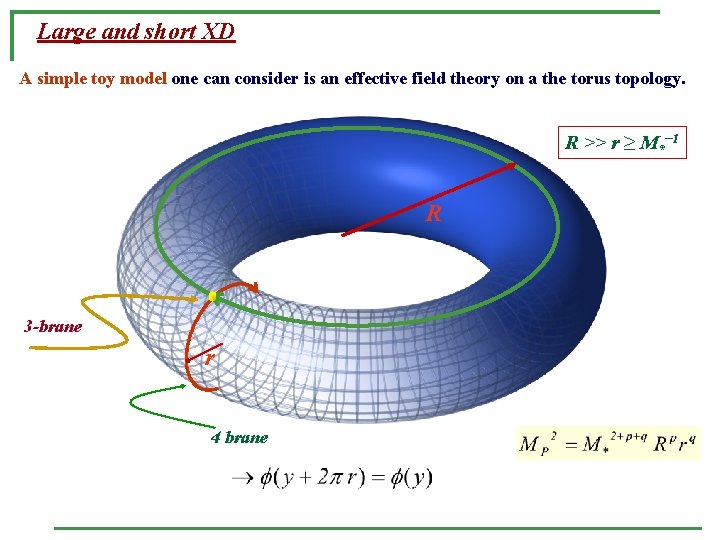
Large and short XD A simple toy model one can consider is an effective field theory on a the torus topology. R >> r ≥ M*− 1 R 3 -brane r 4 brane

Effective Field Theory Prescriptions To begin with, • We identify M* as the String scale or Quantum Gravity scale, so bellow such a scale we can use an effective field theory approach • We’ll take the brane just as an effective (p+1)D flat surface, inspired on the low energy limit of a p-brane. • As for the compact manifold, we will also assume it flat, with some given coordinates y, such that the brane is localized at some (fixed) point y 0 Thus, we need to describe a theory containing fields living on the brane (as SM fields) and in the bulk (as gravity and perhaps SM singlets), as well as the interactions among them.

Effective Field Theory Prescriptions • Bulk fields are described by the higher dimensional action as S is dimensionless: • 3 -Brane fields, as usual, are described by a four dimensional action, which is easily promoted into a 4 + n dimensional expression • Brane-Bulk field interactions are localized on space

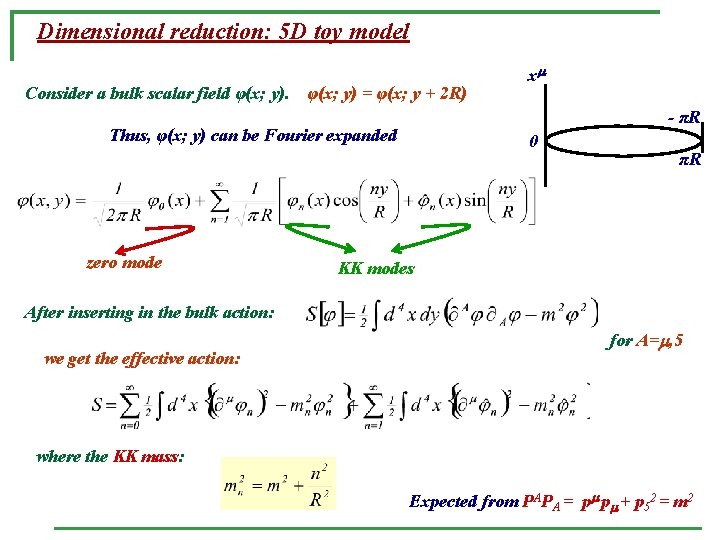
Dimensional reduction: 5 D toy model Consider a bulk scalar field φ(x; y) = φ(x; y + 2 R) - πR Thus, φ(x; y) can be Fourier expanded zero mode x 0 πR KK modes After inserting in the bulk action: we get the effective action: for A= , 5 where the KK mass: Expected from PAPA = p p + p 52 = m 2

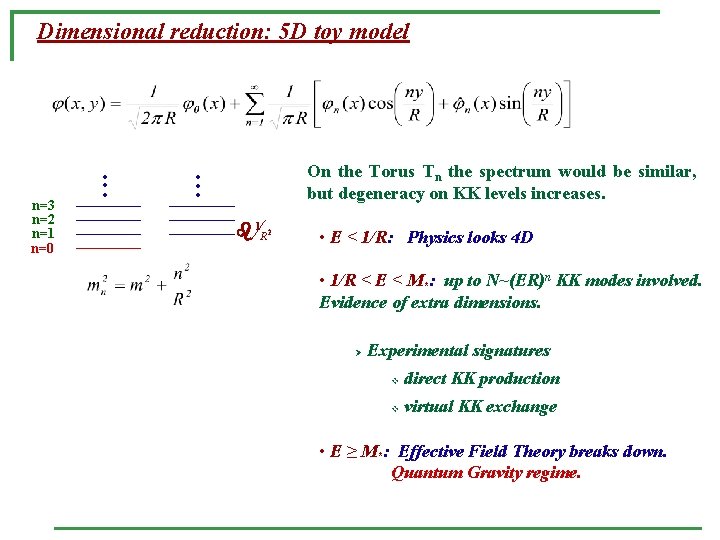
Dimensional reduction: 5 D toy model n=3 n=2 n=1 n=0 • • • On the Torus Tn the spectrum would be similar, but degeneracy on KK levels increases. • • • b 1 R 2 • E < 1/R: Physics looks 4 D • 1/R < E < M*: up to N~(ER)n KK modes involved. Evidence of extra dimensions. Ø Experimental signatures v direct KK production v virtual KK exchange • E ≥ M*: Effective Field Theory breaks down. Quantum Gravity regime.

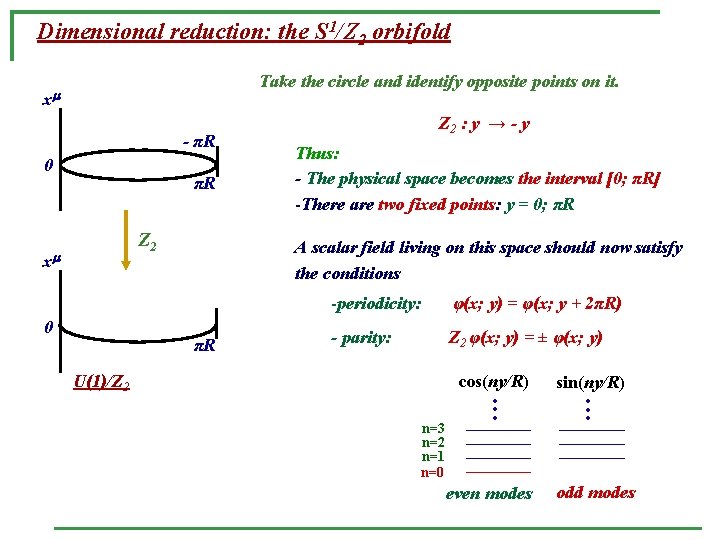
Dimensional reduction: the S 1/Z 2 orbifold Take the circle and identify opposite points on it. x - πR 0 πR Z 2 x 0 Z 2 : y → - y Thus: - The physical space becomes the interval [0; πR] -There are two fixed points: y = 0; πR A scalar field living on this space should now satisfy the conditions πR -periodicity: φ(x; y) = φ(x; y + 2πR) - parity: Z 2 φ(x; y) = ± φ(x; y) U(1)/Z 2 n=3 n=2 n=1 n=0 cos(ny/R) • • • sin(ny/R) • • • even modes odd modes

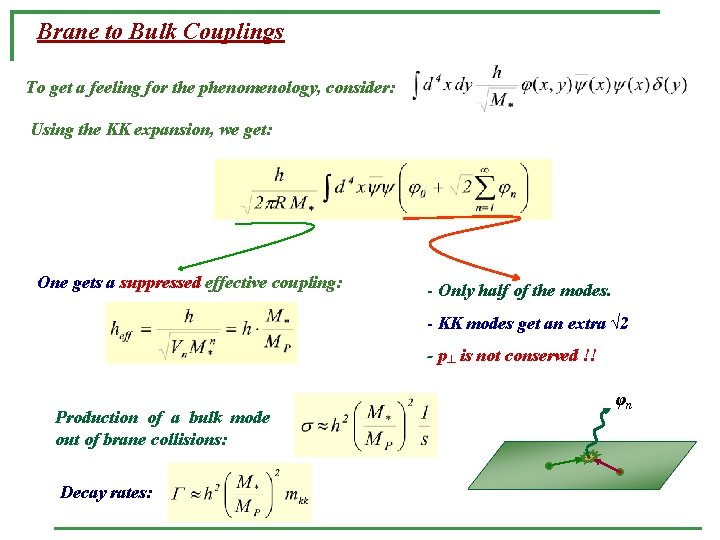
Brane to Bulk Couplings To get a feeling for the phenomenology, consider: Using the KK expansion, we get: One gets a suppressed effective coupling: - Only half of the modes. - KK modes get an extra √ 2 - p┴ is not conserved !! Production of a bulk mode out of brane collisions: Decay rates: φn

KK exchange by brane fields • Consider the effectuve interaction • By summing up (5 D): • At low energies, q 2 << m 2 << 1/R 2 , we get: • At high energies, q 2 >> 1/R 2, on the other hand: since N = MR = MP 2 / M*2

Bulk to Bulk Coupling Suppression Take for instance the coupling in 5 D on [ -πR, πR ] Integrating over the extra dimension we shall get Orthogonality implies p k k± p Fifth momentum is “conserved” in a way that does not constrain the actual direction of the transverse component ( the sign of p 5 is “irrelevant” ) Actually, former p 5 conservation is now manifested only as a parity: (-1 )KK We’ll come back to the orbifold latter…

The Graviton Giudice, Ratazzi & Wells, NPB 544, 3 (1999) Han, Lykken & Zhang, PRD 59, 105006 (1999) Take the action for a particle on the brane and consider the perturbed metric g MN ® h MN + 2 M 11+ n / 2 h MN * h. MN is a symmetric tensor, + general coordinates invariance of GR, implies: D(D - 3)/2 independent deg. of freedom we get, at first order in h the Matter to graviton effective coupling where Possible physical processes are: i) Graviton exchange ii) Graviton emission

Gravity at short distances At the classical limit Graviton exchange should provide the law for Gravitational interactions Existence of extra dimensions could be probed by short distance gravity experiments At large distances, gravity would appear as effectively four dimensional: At short distances, however, it would reveal its higher dimensional nature Both regimes do match : At intermediate scales, just above threshold: But, … How large could R be? . . .

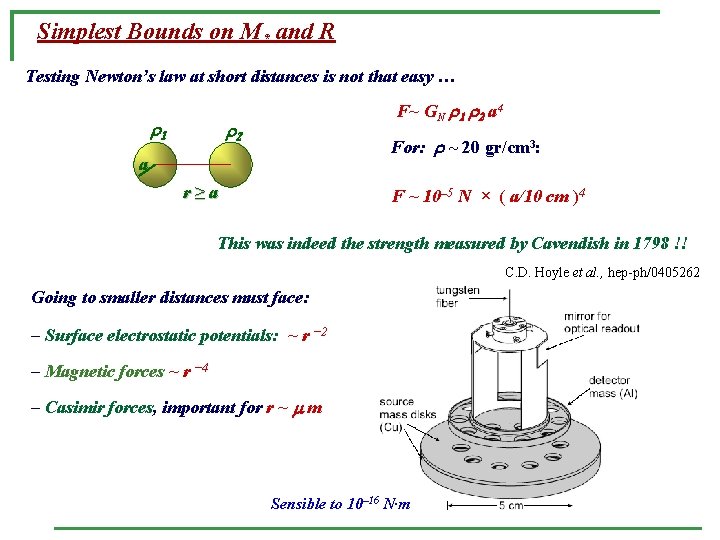
Simplest Bounds on M* and R Testing Newton’s law at short distances is not that easy … r 1 F~ GN r 1 r 2 a 4 r 2 For: r ~ 20 gr/cm 3: a r≥a F ~ 10– 5 N × ( a/10 cm )4 This was indeed the strength measured by Cavendish in 1798 !! C. D. Hoyle et al. , hep-ph/0405262 Going to smaller distances must face: – Surface electrostatic potentials: ~ r − 2 – Magnetic forces ~ r − 4 – Casimir forces, important for r ~ m Sensible to 10– 16 N·m

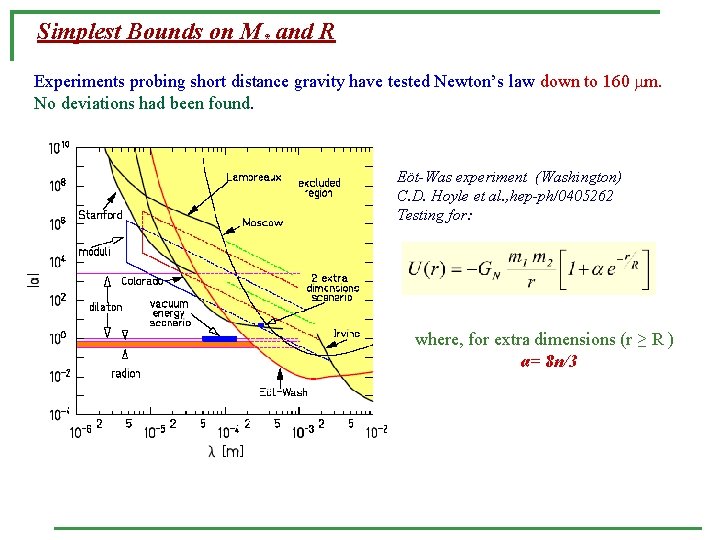
Simplest Bounds on M* and R Experiments probing short distance gravity have tested Newton’s law down to 160 m. No deviations had been found. Eöt-Was experiment (Washington) C. D. Hoyle et al. , hep-ph/0405262 Testing for: where, for extra dimensions (r ≥ R ) α= 8 n/3

Simplest Bounds on M* and R Consider Thus, R < 160 m or equivalently 1 R ³ 10 - 3 e. V On the other hand, from collider physics we know that M* ≥ 1 Te. V For n=1: If we take R < 160 m, then Notice that if we would rather prefer to take M ~ 1 Te. V, say to have a “natural” solution to the hierarchy problem, thus:

Simplest Bounds on M* and R Consider Thus, R < 160 m or equivalently 1 R ³ 10 - 3 e. V On the other hand, from collider physics we know that M* ≥ 1 Te. V For n=2: Lets take again R ≈ 160 m. Now A solution to the Hierarchy Problem? Might such a low fundamental scale be possible? In general, for arbitrary n, with M* ~ 1 Te. V, one gets

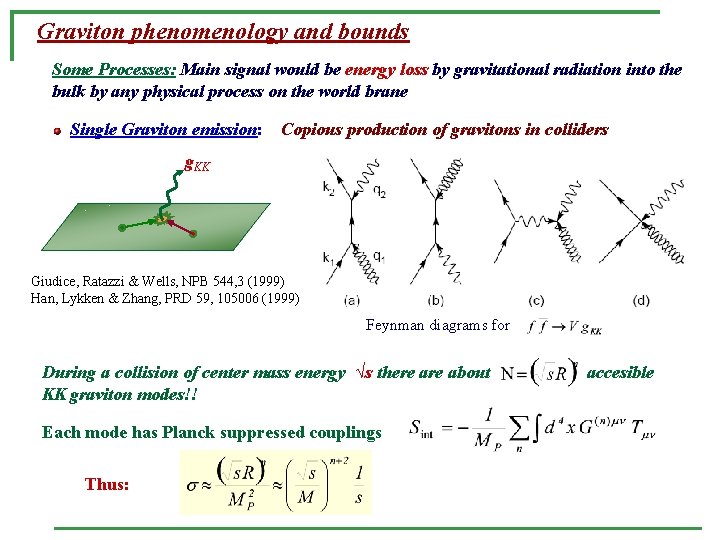
Graviton phenomenology and bounds Some Processes: Main signal would be energy loss by gravitational radiation into the bulk by any physical process on the world brane Single Graviton emission: Copious production of gravitons in colliders g. KK Giudice, Ratazzi & Wells, NPB 544, 3 (1999) Han, Lykken & Zhang, PRD 59, 105006 (1999) Feynman diagrams for During a collision of center mass energy √s there about KK graviton modes!! Each mode has Planck suppressed couplings Thus: accesible

Graviton phenomenology and bounds Giudice, Rattazzi, Wells (1999); Mirabelli, Perelstein, Peskin (1999); Han, Likken, Zhang (1999); Cheung, Keung (1999); Balázs et al. , (1999); Hewet (1999)… LHC: Single JET: p+p− → JET g. KK Drell-Yang: p+p− → ℓ+ℓ− g. KK X Ø Ø Ø ILC: Background: ν ν Ø Feynman diagrams for Background: + ν ν

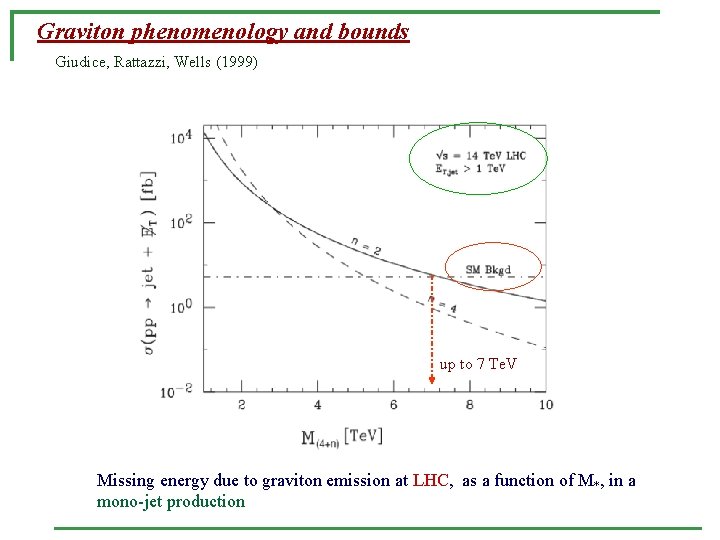
Graviton phenomenology and bounds Giudice, Rattazzi, Wells (1999) up to 7 Te. V Missing energy due to graviton emission at LHC, as a function of M*, in a mono-jet production

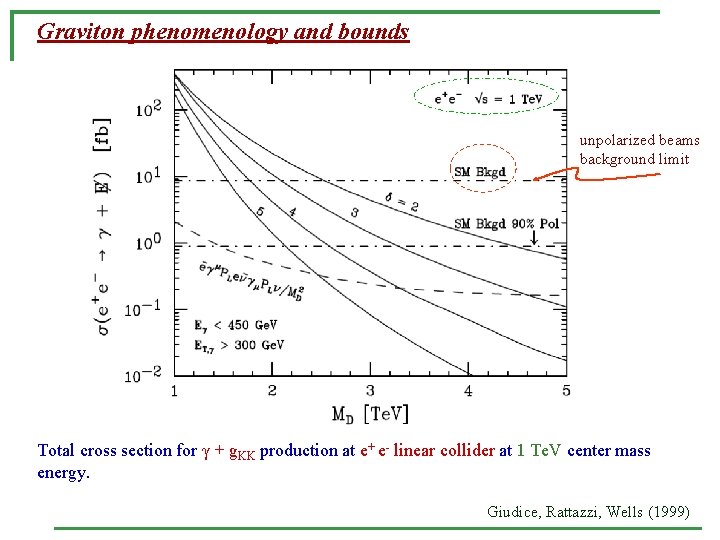
Graviton phenomenology and bounds unpolarized beams background limit Total cross section for γ + g. KK production at e+ e- linear collider at 1 Te. V center mass energy. Giudice, Rattazzi, Wells (1999)

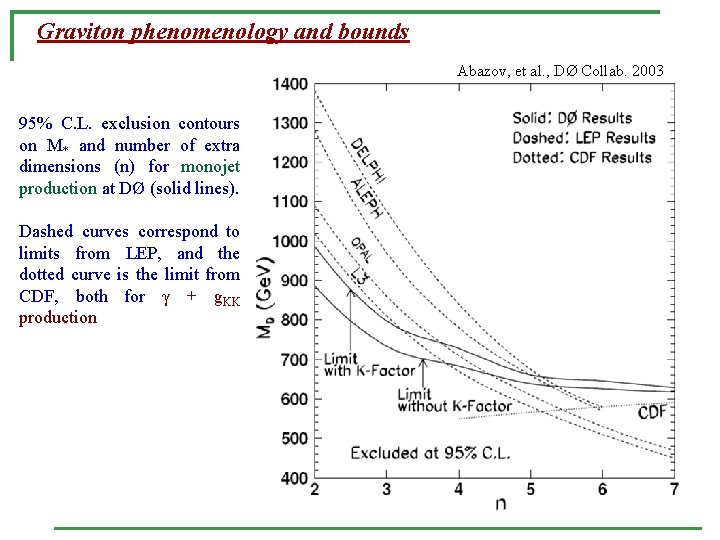
Graviton phenomenology and bounds Abazov, et al. , DØ Collab. 2003 95% C. L. exclusion contours on M* and number of extra dimensions (n) for monojet production at DØ (solid lines). Dashed curves correspond to limits from LEP, and the dotted curve is the limit from CDF, both for γ + g. KK production

Graviton phenomenology and bounds LHC: Ø Ø Single JET: p+p− → JET g. KK Drell-Yang: p+p− → ℓ+ℓ− g. KK X ILC: Explicit computations of graviton emission leads to some bounds: Giudice & Strumia, 2003 • Based on Vn=Rn • Relaxed if one takes different radii 95% CL limits on M* (in Te. V) for n extra dimensions from graviton emission processes in differente experiments

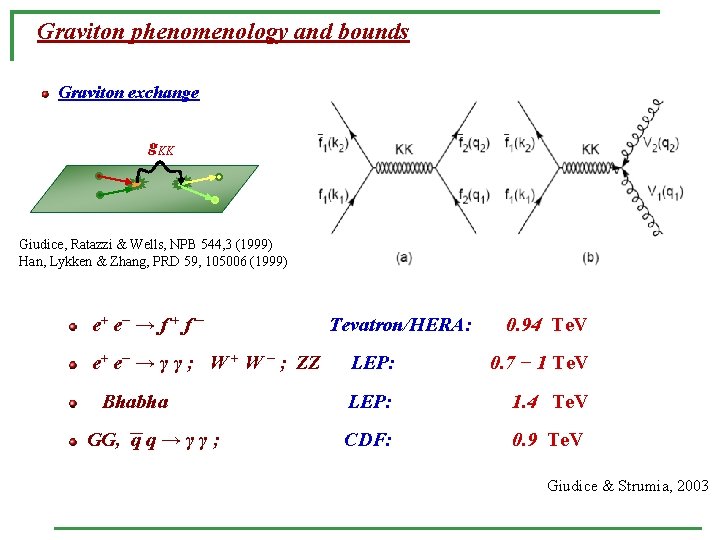
Graviton phenomenology and bounds Graviton exchange g. KK Giudice, Ratazzi & Wells, NPB 544, 3 (1999) Han, Lykken & Zhang, PRD 59, 105006 (1999) e+ e− → f + f − e+ e− → γ γ ; W + W − ; ZZ Bhabha GG, q q → γ γ ; Tevatron/HERA: 0. 94 Te. V LEP: 0. 7 − 1 Te. V LEP: 1. 4 Te. V CDF: 0. 9 Te. V Giudice & Strumia, 2003

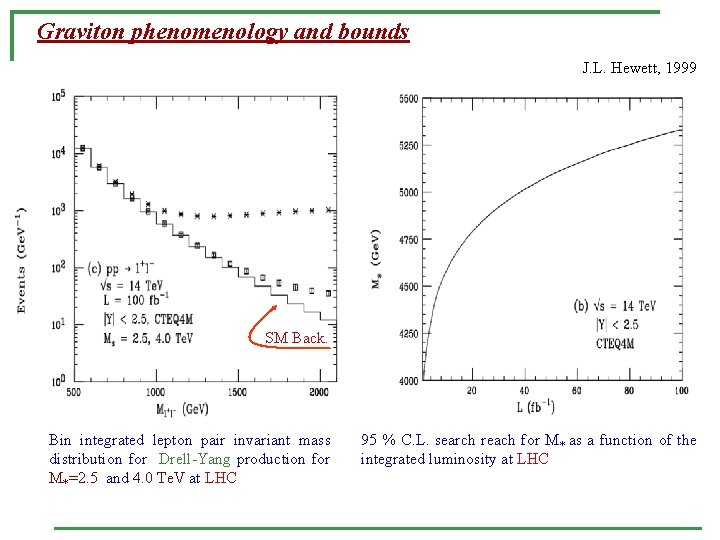
Graviton phenomenology and bounds J. L. Hewett, 1999 SM Back. Bin integrated lepton pair invariant mass distribution for Drell-Yang production for M*=2. 5 and 4. 0 Te. V at LHC 95 % C. L. search reach for M* as a function of the integrated luminosity at LHC

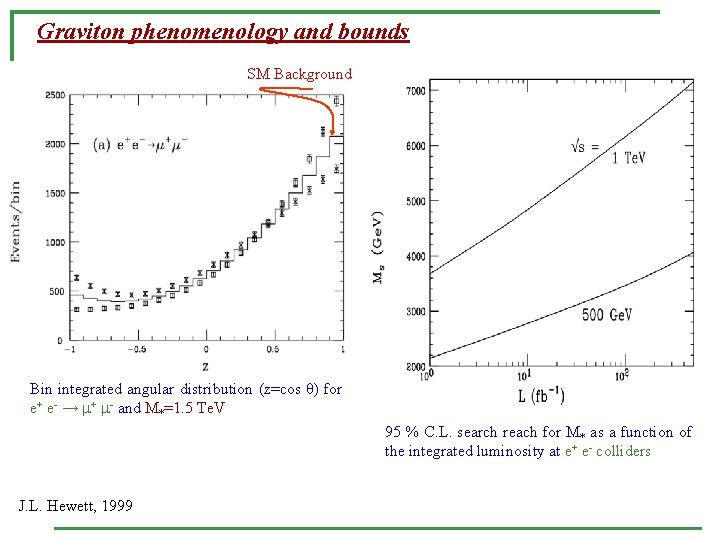
Graviton phenomenology and bounds SM Background Bin integrated angular distribution (z=cos θ) for e+ e- → + - and M*=1. 5 Te. V 95 % C. L. search reach for M* as a function of the integrated luminosity at e+ e- colliders J. L. Hewett, 1999

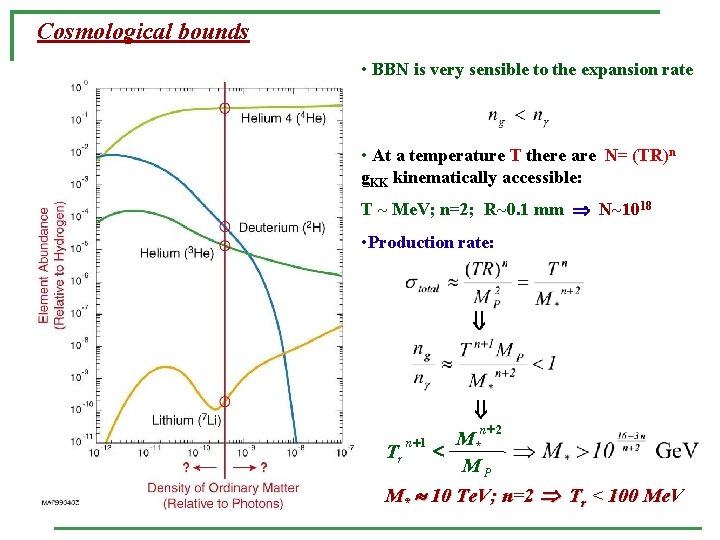
Cosmological bounds • BBN is very sensible to the expansion rate • At a temperature T there are N= (TR)n g. KK kinematically accessible: T ~ Me. V; n=2; R~0. 1 mm N~1018 • Production rate: n+ 2 M* Tr < MP M* 10 Te. V; n=2 Tr < 100 Me. V n +1

Astrophysical bounds Hannestad & Raffelt PRD 64 (2001); PRL 88 (2002) SN 1987 a : → 30 Te. V ( n=2 ) EGRET : GRO: M* > 500 Te. V Neutron star heating: M* > 1700 Te. V These bounds: Ø Assume no short extra dimensions, and apply only for R < Me. V− 1 Ø Assume no graviton decay into ligther KK modes gkk → g. KK + g. KK Mohapatra, Nussinov & Pérez-Lorenzana, PRD 68 (2003)

Microscopic Black Holes Microscopic Black Hole production S. B. Giddings, S. Thomas, PRL 65 (2002) 056010 S. Dimopoulos, G. Landsberg, PRL 87 (2001) 161602 If M* ~ Te. V, we may be exploring effects of Quantum Gravity in LHC/ILC In (4+n)D Schwarzschild radious: If impact parameter in a collision is smaller than r. S, a BH will form MBH = √s Cross section: About 107 BH’s per year LHC !!! (? ). Rapid evaporation:

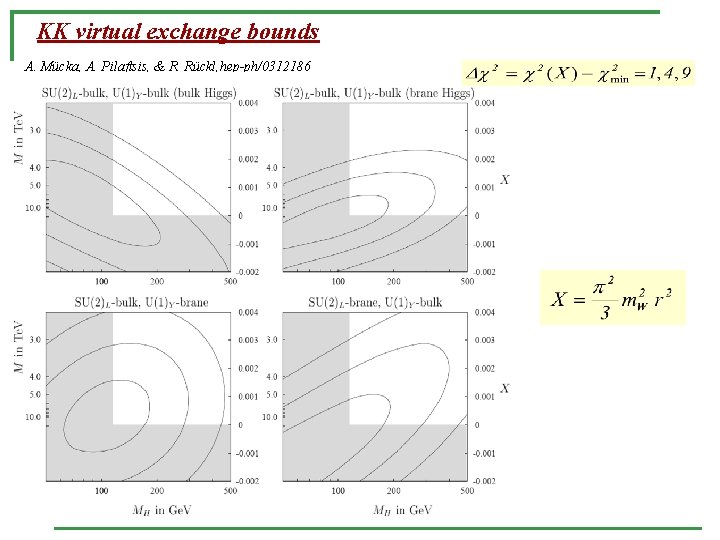
KK virtual exchange bounds A. Mücka, A. Pilaftsis, & R. Rückl, hep-ph/0312186