Physics of Colloids Introduction Types of Colloids Characterization

Physics of Colloids • • Introduction Types of Colloids Characterization of colloidal particles Physical processes between atoms and between colloidal particles

Colloids - Introduction • In between atomic physics and classical physics neglected realm till ~1950 • Colloidal particle: Size of between 1 nm to 1 μm • Theory of colloids 1909, Wolfgang Ostwald, The Nobel Prize in Chemistry • Colloidal system: Colloidal particles (1 nm – 1 μ) dispersed or agglomerated in matrix

Carbon Black (CB): Aggregates of Colloidal Particles - 1 μm

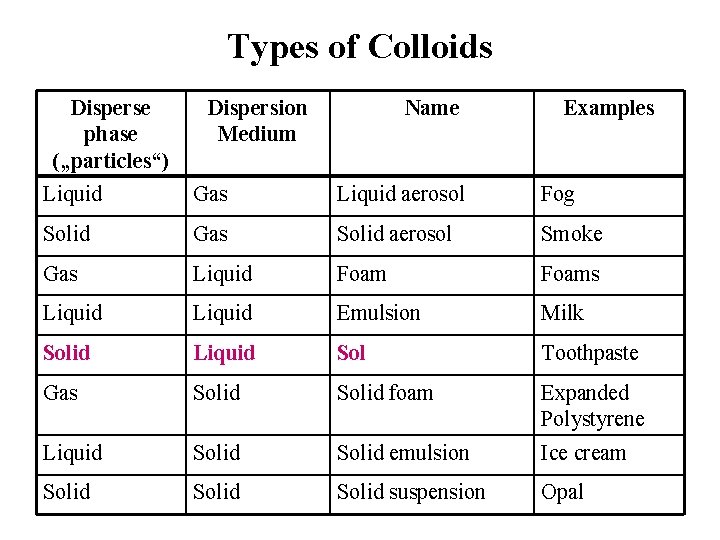
Types of Colloids Disperse phase („particles“) Dispersion Medium Name Examples Liquid Gas Liquid aerosol Fog Solid Gas Solid aerosol Smoke Gas Liquid Foams Liquid Emulsion Milk Solid Liquid Sol Toothpaste Gas Solid foam Expanded Polystyrene Liquid Solid emulsion Ice cream Solid suspension Opal

Applied Coloids • Areas where colloids are used: Toner Pastes Tires Paints Foam Ice Cream

Characterization of colloidal particles • Microscopical – optical, TEM, SPM, • Sedimentation methods (gravitational or centrifugal forces) • Small-angle light (laser) scattering (SALS) 10 -600 nm • Small-angle x-ray scattering (SAXS) 1 -100 nm

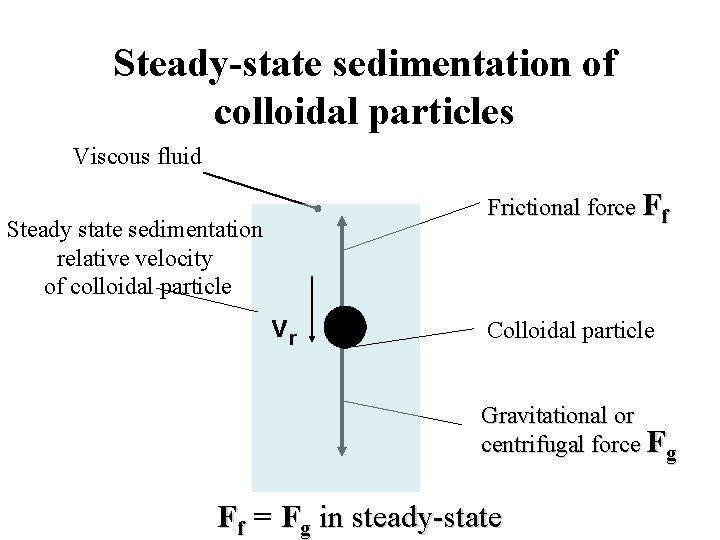
Steady-state sedimentation of colloidal particles Viscous fluid Frictional force Ff Steady state sedimentation relative velocity of colloidal particle vr Colloidal particle Gravitational or centrifugal force Fg Ff = Fg in steady-state

Stokes' law • Frictional force Ff exerted on small spherical particle of radius R in a fluid of dynamic viscosity μ (Pas) induces the relative velocity of the partical • The weight of the particle Fg = (mp - ml)g = 4/3πR 3(ρp - ρf) g = Ff in steady-state (equilibrium Fg = Ff). The sedimentation velocity vs = vr (downwards if ρp > ρf or upwards if ρp < ρf ) where ρp and ρf are the mass density of the particles and fluid resp. (kg/m 3), g is gravitational acceleration (9. 81 m/s 2) E. g. , carbon black particles in water ((ρp –ρf) = 1000 kg/m 3, μ = 0. 001 Pas): a) radius of particles R = 1000 nm → vs = 0. 7848 nm/hour, and the distance 0. 1 m takes 12. 74 hours (consistent with common experimental time → the real sedimentation). b) radius of particles R = 10 nm → vs = 0. 07848 nm/hour and the distance 0. 1 m takes 53 days (substantial longer than common experimental time → kinetic stability)

Brownian motion • • The particles move around under the influences of gravity and Brownian motion (thermal agitation) The kinetic energy transferred to a particle depends on the temperature, being equal to 3 k. T/2, where k = 1. 38 x 10 -23 J/K is Boltzmann constant and T thermodynamic temperature

Thermal Agitation Thermal agitation at temperature T>0 opposes sedimentation of particles. Boltzmann’s law describes the equilibrium distribution of the spheres of radius R Potential energy of particle Average heat energy of particle C(h) h C 0 C(h) … particle concentration at high h, C 0 … particle concentration at the bottom m … effective mass of each particle, g … acceleration due to gravity, k … Boltzmann constant 1. 36 E-23 J/K ρp, ρf. . . mass density of partical and fluid, respectively Example (ρp – ρf) = 1000 kg/m 3, T = 300 K, h = 0. 1 m, then for R = 100 nm is C(h)/C 0 = 10 -430 ~ 0 , for R = 10 nm is C(h)/C 0 = 0. 9 (Thermal stability)

Colloidal Systems Transformation • To induce separation of the two phases present Cloudy wine (due to some unwelcome fermentation): pouring egg white into the barrel, while stirring it. The egg white causes organic particles in suspension to form aggregates, they sediment and the clean wine appears. • To purify water Dirty particles agglomerate by addition an salt. Sufficient large agglomerates sediment or form crust (it is called flocculation).

Two preconditions of aggregation of particles 1) Movement of particles (transportable environment, e. g. Gravitation or Brownian motion) 2) Specific interactions between particles (to catch the particles)

Spontaneous growth of fractal by DLA of colloidal particles enabled by their Brownian motion :

Spontaneous and directed growth of structures 1) Spontaneous growth in nature • Many various species evolution (including blind passages) optimal structure • Very slow process feasible only in milions of years 2) Directed growth • Design nanotechnology (bottom-up process) useful (functional) structures • Very slow process – till now not feasible technology 3) Directed spontaneous growth (assisted growth) • Application of knowledge of interactions between the particles of the structure (bio-mimetics)

Typical significant interactions between nanoparticles: • Van der Waals attractive forces • Electrostatic repulsive forces on long distance

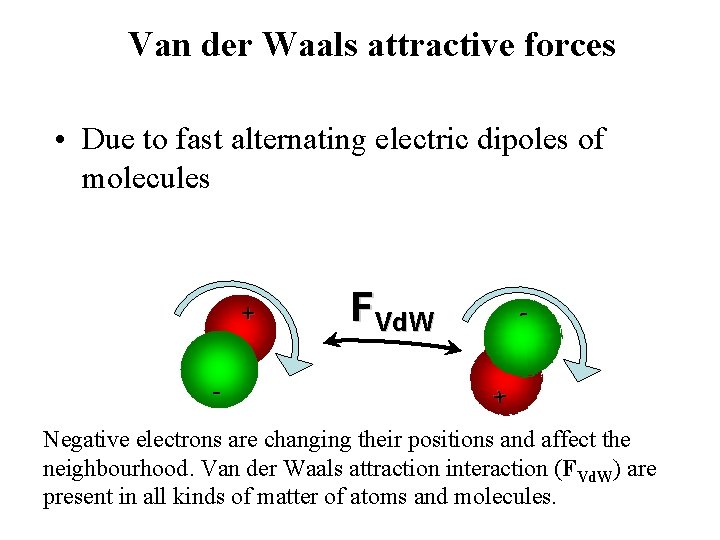
Van der Waals attractive forces • Due to fast alternating electric dipoles of molecules + - FVd. W - + Negative electrons are changing their positions and affect the neighbourhood. Van der Waals attraction interaction (FVd. W) are present in all kinds of matter of atoms and molecules.

Potential energy of van der Waals attraction forces between two atoms β EW is inversely related to x 6 ! h. . . Planck constant, 1 , 2. . . characteristic frequency of electrons, 1 , 2. . . polarization ability od dipoles, 0. . permitivity of vaccum, x. . . distance between atoms

Lennard – Jones potential (interaction of two atoms) Interaction energy ELJ x x 0: equilibrium of van der Waals forces and repulsive forces of short distance ELJ = ERS - EW Vd. W Repulsion energy on short dist. ERS Total interaction energy ELJ E 0 van der Waals energy 1 0. EW x 0 -1 nm Atom. distance x constants , , . . . constants

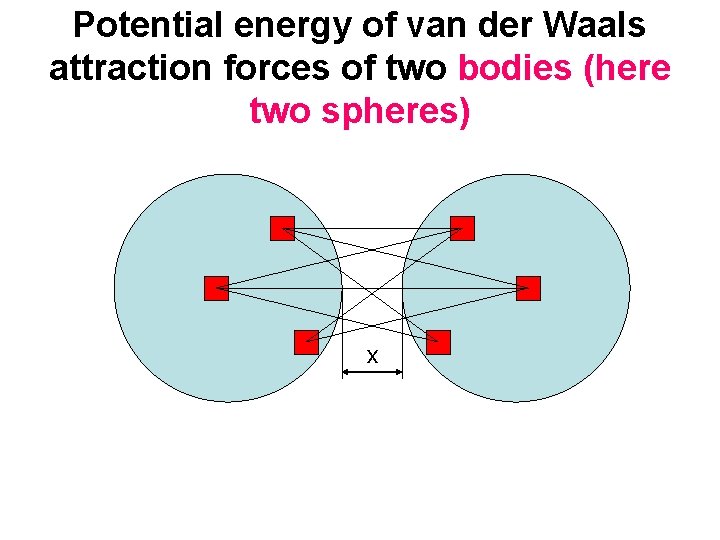
Potential energy of van der Waals attraction forces of two bodies (here two spheres) x

Van der Waals forces are additive. If the number of atoms per m 3 is (m-3), then the pair interaction between volumes of bodies d. V 1 a d. V 2 in distance x The sume of attraction energy is the integration over the volumes of both the bodies The solution gives the total energy EW (x) between all atoms of both bodies in separation of their surfaces x. E. g. , for two equal spheres of radius R >> x H (J) … Hamaker constant, depends on materials of bodies and environment. EW ~ 1/x, inversely related to x. Much larger action radius than atoms!

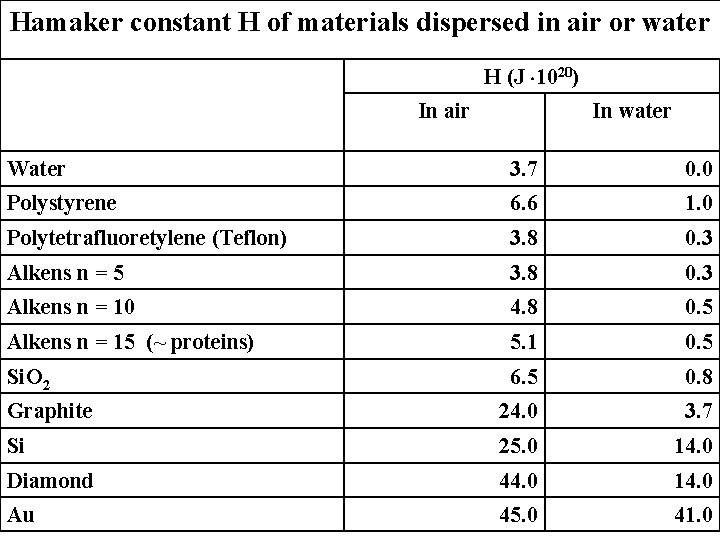
Hamaker constant H of materials dispersed in air or water H (J 1020) In air In water Water 3. 7 0. 0 Polystyrene 6. 6 1. 0 Polytetrafluoretylene (Teflon) 3. 8 0. 3 Alkens n = 5 3. 8 0. 3 Alkens n = 10 4. 8 0. 5 Alkens n = 15 (~ proteins) 5. 1 0. 5 Si. O 2 6. 5 0. 8 Graphite 24. 0 3. 7 Si 25. 0 14. 0 Diamond 44. 0 14. 0 Au 45. 0 41. 0

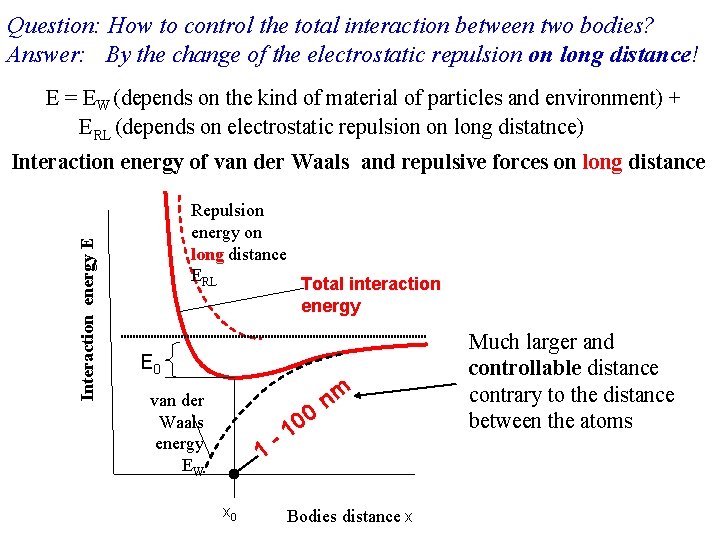
Question: How to control the total interaction between two bodies? Answer: By the change of the electrostatic repulsion on long distance! E = EW (depends on the kind of material of particles and environment) + ERL (depends on electrostatic repulsion on long distatnce) Interaction energy E Interaction energy of van der Waals and repulsive forces on long distance Repulsion energy on long distance ERL Total interaction energy E 0 van der Waals energy EW 1 x 0 - 0 0 1 nm Bodies distance x Much larger and controllable distance contrary to the distance between the atoms

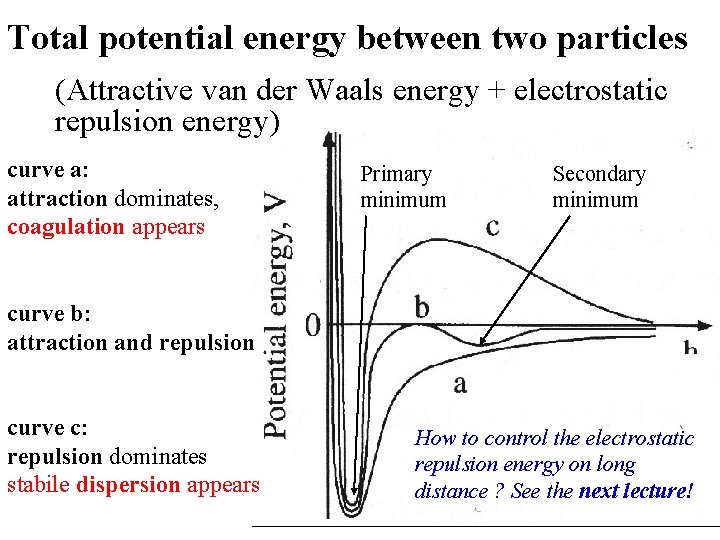
Total potential energy between two particles (Attractive van der Waals energy + electrostatic repulsion energy) curve a: attraction dominates, coagulation appears curve b: attraction and repulsion curve c: repulsion dominates stabile dispersion appears Primary minimum Secondary minimum x How to control the electrostatic repulsion energy on long distance ? See the next lecture!