Physics Chapter 7 Motion in Two Dimensions Objectives

Physics: Chapter 7 Motion in Two Dimensions

Objectives By the end of this chapter, you should be able to: • Explain how the equations for projectile motion are derived. • Solve projectile motion problems. • Solve circular motion problems. • Solve pendulum motion problems.

Objectives By the end of this chapter, you should be able to: • To understand the definition of simple harmonic motion and apply it to spring and pendulum motion. • To experimentally determine the relationship velocity and centripetal force.

Explain how the equations for projectile motion are derived. • Projectile motion is the motion of an object after it is projected into the air and the only force on the object is gravity (we will neglect the effects of air resistance. ) • Since gravity is the only force on the object, the only acceleration of the object is 9. 8 m/s 2, downward.

Explain how the equations for projectile motion are derived. • From our knowledge of vectors, we know that vectors that act perpendicularly to each other have no effect on each other. • In other words, the horizontal motion of the projectile is completely independent of its vertical motion. • So the force (and acceleration) on the projectile in the vertical dimension has no bearing on the horizontal dimension.

Explain how the equations for projectile motion are derived. • It is this independence property of perpendicular vectors that allows us to break up projectile motion into two separate parts, horizontal and vertical. • The vertical direction consists of accelerated motion. (a = g = -9. 8 m/s 2) • The horizontal direction consists of constant velocity motion. (a = 0)

Explain how the equations for projectile motion are derived. • The motion equations from chapter 3 are simply applied to each dimension separately. • Lets review the equations used in chapter 3.

Explain how the equations for projectile motion are derived. · • DS = VDt (a more useful form of V = DS/Dt) Vf = Vi + a. Dt (a useful form of a = DV/Dt) DS = Vi. Dt + 1/2 a. Dt 2 Vf 2 = Vi 2 + 2 a. DS

Explain how the equations for projectile motion are derived. • • · • Horizontal direction Constant velocity DSx = Vx. Dt The rest of the equations do not apply since they involve acceleration. • Vertical direction • Acceleration = -g (-9. 8 m/s 2) • The first equation does no apply since it is for constant velocity. • Vy = Viy - g. Dt · DSy = Viy. Dt - 1/2 g. Dt 2 • Vy 2 = Viy 2 - 2 g. DSy

Solve projectile motion problems. • Some tips to solve projectile motion problems. • Never mix horizontal and vertical information in the same equation.

Solve projectile motion problems. • Some more tips to solve projectile motion problems. • Time is the only quantity that can be used in both directions (since it is a scalar it is not associated with either). Time links the two dimensions together.

Solve projectile motion problems. • Some additional tips to solve projectile motion problems. • There is a great deal of symmetry to projectile motion. • The vertical velocity upward at the beginning = the vertical velocity downward at the end. (Vfy = Viy) • The vertical velocity at the highest point is zero. • The time up to top = the time to fall back down.

Practice Problem (“we do”) A rock is thrown horizontally off of a 100 m cliff and lands 95 m away. At what speed was it thrown?

Practice Problem (“we do”) A car drives horizontally off of a cliff at 15 m/s. It lands 30 m from the base of the cliff. How high is the cliff?

(“you do”) Example projectile motion problem #1. A ball is projected horizontally out of a second story window with a velocity of 15 m/s. The window is 10. 0 m above the ground. How far from the house does the ball land? Vix DSy DSx Step 1: Draw a labeled diagram. Vix = 15 m/s Viy = 0 (horizontally projected) Dsy = -10. 0 m (- means down) DSx = ? g = 9. 8 m/s 2 , the negative is built into the equations already. t = ______ , this is the link between the two dimensions. Step 2: Identify given information.

Example projectile motion problem #1. The plan is to use one direction’s information to find the time, and then use the time to find the question in the other direction. Vix = 15 m/s Dsy = -10 m DSx= ? DSx = Vx. Dt DSx = (15 m/s) ( 1. 43 sec) DSx = 21. 4 m DSy = Viy. Dt - 1/2 g. Dt 2 -10. 0 m = -1/2 (9. 8) Dt 2 Dt = 1. 43 sec. Note: The Three-Box Format will be used this chapter!

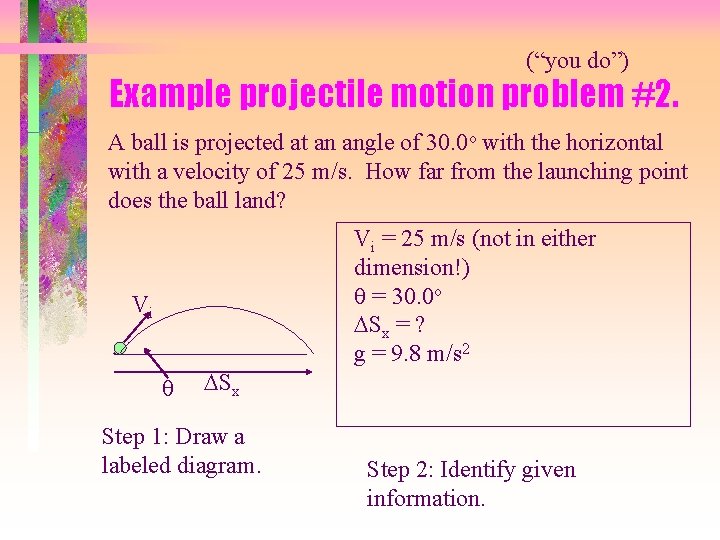
(“you do”) Example projectile motion problem #2. A ball is projected at an angle of 30. 0 o with the horizontal with a velocity of 25 m/s. How far from the launching point does the ball land? Vi q DSx Step 1: Draw a labeled diagram. Vi = 25 m/s (not in either dimension!) q = 30. 0 o DSx = ? g = 9. 8 m/s 2 Step 2: Identify given information.

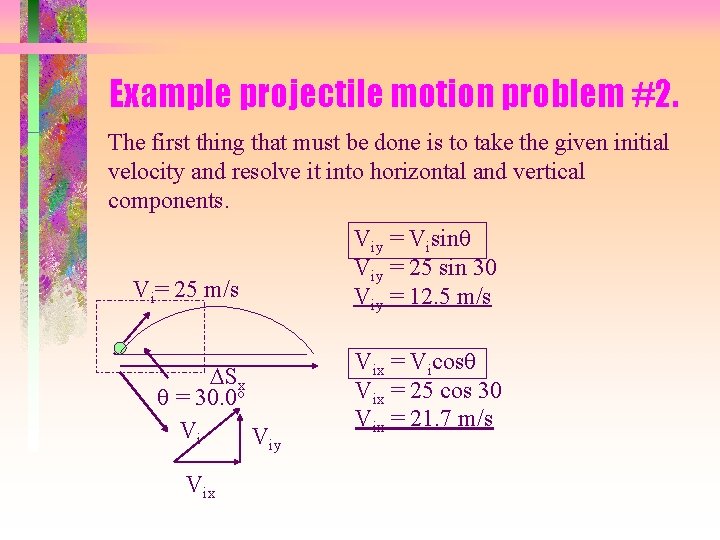
Example projectile motion problem #2. The first thing that must be done is to take the given initial velocity and resolve it into horizontal and vertical components. Vi= 25 m/s DSx q = 30. 0 o Vi Viy Vix Viy = Visinq Viy = 25 sin 30 Viy = 12. 5 m/s Vix = Vicosq Vix = 25 cos 30 Vix = 21. 7 m/s

Example projectile motion problem #2. The next task to do is to figure out how long the projectile is in the air. Remember: Vfy = -Viy Vi= 25 m/s DSx q = 30. 0 o Vy = Viy - g. Dt -12. 5 = 12. 5 - 9. 8 Dt Dt = 2. 55 sec.

Example projectile motion problem #2. Now we have enough information to solve the question. Vi= 25 m/s DSx q = 30. 0 o DSx = Vx. Dt DSx = (21. 7)(2. 55) DSx = 55. 4 m

(“you do”) Example projectile motion problem #3. Using the same information as #2, find the maximum height the projectile reaches. This is another classic problem. Vi= 25 m/s DSy q = 30. 0 o To solve this problem most efficiently, you only need ydimension information. Viy = 12. 5 m/s (see Prob. #2) Vy = 0 (at top of path) g = 9. 8 m/s 2 Vy 2 = Viy 2 - 2 g. DSy 02 = 12. 52 - 2(9. 8) Dsy DSy = 7. 97 m

Solve circular motion problems. • Circular motion problems are considerably easier than projectile motion. • We will be considering constant speed circular motion. Does this mean constant Velocity? • No! Velocity is a vector. As the direction changes , so does the velocity. • This means there is acceleration even though the speed is constant.

Solve circular motion problems. • Centripetal Acceleration is found by • ac = V 2/r, where V is the object’s speed, and r is the radius of the circular path. • Centripetal (meaning “Center Seeking”) Acceleration is always directed toward the center of the curved path.

Solve circular motion problems. • • • Centripetal Force is found by Fc = m. V 2/r, where m is the object’s mass. Note that this is Newton’s Second Law Fc = mac Centripetal (meaning “Center Seeking”) Force is always directed toward the center of the curved path. • The velocity of the object is always directed tangent to the curved path.

Solve pendulum motion problems. • The period of a pendulum (time for one complete swing) is found by • T = 2 p L/g • T is the period, L is the length of the pendulum in meters, and g is of course the acceleration due to gravity.

Assignments • Bookwork Part 1: Section problems 1 -20 odd; End questions 1, 2, 6; End Prob-A 1 -8 odd (due Mon. 11/6) Part 2: Section problems 1 -20 even; End Prob-A 1 -8 even (due Thurs. 11/9) • Lab report. (Tues. 11/14) • Review Sheets. (Fri. 11/10) • Test. (Mon. 11/13)